Hostname: page-component-7dd5485656-pnlb5 Total loading time: 0.001 Render date: 2025-10-31T21:40:21.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Distal Actions of Automorphisms of Lie Groups G on SubG

Part of: Topological dynamics Locally compact groups and their algebras Lie groups

Published online by Cambridge University Press:  21 December 2021

RIDDHI SHAH  and
ALOK KUMAR YADAV
RIDDHI SHAH
Affiliation:
School of Physical Sciences, Jawaharlal Nehru University, New Delhi 110067, India, e-mail: riddhi.kausti@gmail.com, rshah@jnu.ac.in
ALOK KUMAR YADAV*
Affiliation:
Department of Mathematical Sciences, Indian Institute of Science Education and Research, Mohali 140306, India, e-mail: alokmath1729@gmail.com
*
†Corresponding author: Alok Kumar Yadav
Get access Rights & Permissions [Opens in a new window]

Abstract

For a locally compact metrisable group G, we study the action of 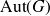${\rm Aut}(G)$ on 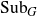${\rm Sub}_G$, the set of closed subgroups of G endowed with the Chabauty topology. Given an automorphism T of G, we relate the distality of the T-action on 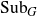${\rm Sub}_G$ with that of the T-action on G under a certain condition. If G is a connected Lie group, we characterise the distality of the T-action on 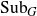${\rm Sub}_G$ in terms of compactness of the closed subgroup generated by T in 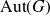${\rm Aut}(G)$ under certain conditions on the center of G or on T as follows: G has no compact central subgroup of positive dimension or T is unipotent or T is contained in the connected component of the identity in 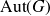${\rm Aut}(G)$. Moreover, we also show that a connected Lie group G acts distally on 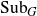${\rm Sub}_G$ if and only if G is either compact or it is isomorphic to a direct product of a compact group and a vector group. All the results on the Lie groups mentioned above hold for the action on 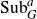${\rm Sub}^a_G$, a subset of 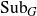${\rm Sub}_G$ consisting of closed abelian subgroups of G.

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 22D45: Automorphism groups of locally compact groups 22E25: Nilpotent and solvable Lie groups 22E15: General properties and structure of real Lie groups

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 2 , September 2022 , pp. 457 - 478
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abels, H.. Distal affine transformation groups. J. Reine Angew. Math. 299/300 (1978), 294–300.Google Scholar
Abels, H.. Distal automorphism groups of Lie groups. J. Reine Angew. Math. 329 (1981), 82–87.Google Scholar
Arens, R.. Topologies for homeomorphism groups. Amer. J. Math. 68 (1946), 593–610.10.2307/2371787CrossRefGoogle Scholar
Abert, M., Bergeron, N., Biringer, I., Gelander, T., Nikolov, N., Raimbault, J. and Samet, I.. On the growth of $L^2$ -invariants for sequences of lattices in Lie groups. Ann. of Math. (2) 185 (2017), 711–790.Google Scholar
Baik, H. and ClavierL, L.. The space of geometric limits of one-generator closed subgroups of ${\rm PSL}_2({\mathbb R})$ . Algebr. Geom. Topol. 13 (2013), 549–576.10.2140/agt.2013.13.549CrossRefGoogle Scholar
Baik, H. and Clavier, L.. The space of geometric limits of abelian subgroups of ${\rm PSL}_2({\mathbb C})$ . Hiroshima Math. J. 46 (2016), 1–36.10.32917/hmj/1459525928CrossRefGoogle Scholar
Benedetti, R. and Petronio, C.. Lectures on Hyperbolic Geometry (Springer-Verlag, 1992).10.1007/978-3-642-58158-8CrossRefGoogle Scholar
Bridson, M. R., De La Harpe, P. and Kleptsyn, V.. The Chabauty space of closed subgroups of the three-dimensional Heisenberg group. Pacific J. Math. 240 (2009), 1–48.10.2140/pjm.2009.240.1CrossRefGoogle Scholar
Chabauty, C.. Limite d’ensemble et géométrie des nombres. Bull. Soc. Math. France 78 (1950), 143–151.10.24033/bsmf.1412CrossRefGoogle Scholar
Dani, S. G.. On automorphism groups of connected Lie groups. Manuscripta Math. 74 (1992), 445–452.10.1007/BF02567680CrossRefGoogle Scholar
Dani, S. G. and SHAH, R.. Contractible measures and Lévy’s measures on Lie groups. In: Probability on Algebraic Structures (Ed. G. Budzban P. Feinsilver and A. Mukherjea), Contemporary Math. 261 (2000), 3–13.10.1090/conm/261/04129CrossRefGoogle Scholar
Ellis, R.. Distal transformation Groups. Pacific J. Math. 8 (1958), 401–405.10.2140/pjm.1958.8.401CrossRefGoogle Scholar
Furstenberg, H.. The structure of distal flows. Amer. J. Math. 85 (1963), 477–515.10.2307/2373137CrossRefGoogle Scholar
Hamrouni, H. and KADRI, B.. On the compact space of closed subgroups of locally compact groups. J. Lie Theory 23 (2014), 715–723.Google Scholar
Hazod, W. and SIEBERT, E.. Automorphisms on a Lie group contracting modulo a compact subgroup and applications to semistable convolution semigroups. J. Theoret. Probab. 1 (1988), 211–225.10.1007/BF01046936CrossRefGoogle Scholar
Hochschild, G.. The automorphism group of a Lie group. Trans. Amer. Math. Soc. 72 (1952), 209–216.Google Scholar
Hochschild, G.. The Structure of Lie Groups (Holden-Day,Inc., 1965).Google Scholar
Iwasawa, K.. On some type of topological groups. Annals of Math. II, 50 (1949), 507–558.10.2307/1969548CrossRefGoogle Scholar
Jenkins, J.. Growth of connected locally compact groups. J. Functional Analysis 12 (1973), 113–127.10.1016/0022-1236(73)90092-XCrossRefGoogle Scholar
Knapp, A. W.. Lie Groups Beyond an Introduction. Second Edition. Progr. Math. 140 (BirkhÄuser Boston Inc., 2002).Google Scholar
Moore, C. C.. Distal affine transformation groups. Amer. J. Math. 90 (1968), 733–751.10.2307/2373481CrossRefGoogle Scholar
Previts, W. H. and WU, S. T.. On the group of automorphisms of an analytic group. Bull. Austral. Math. Soc. 64 (2001), 423–433.10.1017/S0004972700019894CrossRefGoogle Scholar
Pourezza, I. and HUBBARD, J.. The space of closed subgroups of ${\mathbb R}^2$ . Topology 18 (1979), 143–146.10.1016/0040-9383(79)90032-6CrossRefGoogle Scholar
Raghunathan, M. S.. Discrete Subgroups of Lie Groups (Springer-Verlag, 1972).Google Scholar
Raja, C. R. E. and SHAH, R.. Distal actions and shifted convolution property. Israel J. Math. 177 (2010), 301–318.10.1007/s11856-010-0052-7CrossRefGoogle Scholar
Raja, C. R. E. and SHAH, R.. Some properties of distal actions on locally compact groups. Ergodic Theory and Dynam. Systems 39 (2019), 1340–1360.Google Scholar
Rosenblatt, J.. A distal property of groups and the growth of connected locally compact groups. Mathematika 26 (1979), 94–98.10.1112/S0025579300009669CrossRefGoogle Scholar
Shah, R.. Orbits of distal actions on locally compact groups. J. Lie Theory 22 (2010), 586–599.Google Scholar
Shah, R.. Expansive automorphisms on locally compact groups. New York J. Math. 26 (2020), 285–302.Google Scholar
Shah, R. and YADAV, A. K.. Dynamics of certain distal actions on spheres. Real Analysis Exchange 44 (2019), 77–88.10.14321/realanalexch.44.1.0077CrossRefGoogle Scholar
Shah, R. and YADAV, A. K.. Distality of certain actions on p-adic spheres. J. Australian Math. Soc. 109 (2020), 250–261.10.1017/S1446788719000272CrossRefGoogle Scholar
Stroppel, M.. Locally Compact Groups. EMS Textbooks in Mathematics (European Math. Soc. - EMS, 2006).Google Scholar
Wigner, D.. On the automorphism group of a Lie group. Proc. Amer. Math. Soc. 45 (1974), 140–143.10.1090/S0002-9939-1974-0357684-0CrossRefGoogle Scholar
Wigner, D.. Erratum to “On the automorphism group of a Lie group”. Proc. Amer. Math. Soc. 60 (1976), 376.Google Scholar
Palit, R. and SHAH, R.. Distal actions of automorphisms of nilpotent groups G on ${\rm Sub}_G$ and applications to lattices in Lie groups. Glasgow Math. Journal, 63 (2021), 343–362.10.1017/S0017089520000221CrossRefGoogle Scholar
Prajapati, M. B. and SHAH, R.. Expansive actions of automorphisms of locally compact groups G on ${\rm Sub}_G$ . Monatsh. Math. (2020), 193 (2020), 129–142.10.1007/s00605-020-01389-5CrossRefGoogle Scholar
Ppalit, R., PRAJAPATI, M. B. and SHAH, R.. Dynamics of actions of automorphisms of discrete groups G on ${\rm Sub}_G$ and applications to lattices in Lie groups. Groups, Geometry, and Dynamics (to appear).Google Scholar