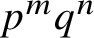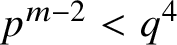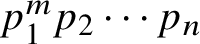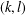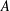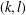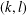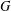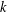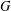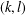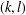Refine search
Actions for selected content:
10 results
Functional degrees and arithmetic applications III: beyond prime exponent
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 30 May 2025, pp. 409-438
- Print publication:
- September 2025
-
- Article
- Export citation
On the structure of spectral and tiling subsets of cyclic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proof of the Brown–Erdős–Sós conjecture in groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 04 July 2019, pp. 323-333
- Print publication:
- September 2020
-
- Article
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
THE MAXIMUM SIZE OF
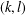 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A STRUCTURED DESCRIPTION OF THE GENUS SPECTRUM OF ABELIAN p-GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 10 July 2018, pp. 381-423
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
Comments on Y. O. Hamidoune's Paper ‘Adding Distinct Congruence Classes’
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 09 March 2016, pp. 641-644
-
- Article
- Export citation
On n-Sums in an Abelian Group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 419-435
-
- Article
- Export citation
Homotopy Formulas for Cyclic Groups Acting on Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 1 / 01 March 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-85
- Print publication:
- 01 March 2008
-
- Article
-
- You have access
- Export citation
CORRIGENDUM: REPLACEMENT OF FACTORS BY SUBGROUPS IN THE FACTORIZATION OF ABELIAN GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 08 February 2005, p. 80
- Print publication:
- January 2005
-
- Article
- Export citation