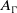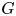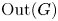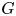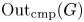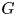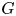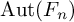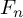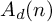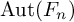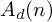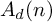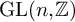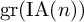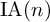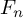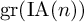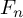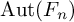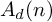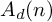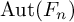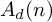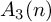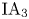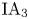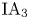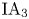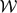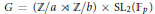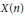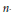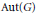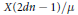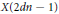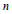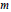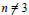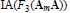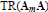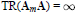Refine search
Actions for selected content:
22 results
A note on morphisms to wreath products
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-28
-
- Article
- Export citation
On the structures of the Johnson cokernels of the basis-conjugating automorphism groups of free groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-29
-
- Article
- Export citation
The Formanek-Procesi group with base a right-angled Artin group: Lie algebra and residual nilpotence
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-22
-
- Article
- Export citation
On automorphisms and splittings of special groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 232-305
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACTIONS OF AUTOMORPHISM GROUPS OF FREE GROUPS ON SPACES OF JACOBI DIAGRAMS. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1-69
- Print publication:
- January 2024
-
- Article
- Export citation
On the low-dimensional cohomology groups of the IA-automorphism group of the free group of rank three
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 338-363
-
- Article
-
- You have access
- Open access
- Export citation
Cube complexes and abelian subgroups of automorphism groups of RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 20 November 2019, pp. 523-547
- Print publication:
- May 2021
-
- Article
- Export citation
CONJUGATING AUTOMORPHISMS OF GRAPH PRODUCTS: KAZHDAN’S PROPERTY (T) AND SQ-UNIVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 272-282
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Duality between p-groups with three characteristic subgroups and semisimple anti-commutative algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 25 February 2019, pp. 1827-1852
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
WEAK CAYLEY TABLE GROUPS OF SOME CRYSTALLOGRAPHIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 635-660
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
Twisted homological stability for extensions and automorphism groups of free nilpotent groups
-
- Journal:
- Journal of K-Theory / Volume 14 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 185-201
- Print publication:
- August 2014
-
- Article
- Export citation
Cohomology rings of almost-direct products of free groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 465-479
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
NORMAL AUTOMORPHISMS OF A FREE METABELIAN NILPOTENT GROUP
-
- Journal:
- Glasgow Mathematical Journal / Volume 52 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 04 December 2009, pp. 169-177
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
NON-TAME AUTOMORPHISMS OF A FREE GROUP OF RANK 3 IN
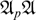
-
- Journal:
- Glasgow Mathematical Journal / Volume 49 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 September 2007, pp. 449-467
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Spherical Space Forms: Homotopy Types and Self-Equivalences for the Group (ℤ/a ⋊ ℤ/b) × SL 2 (
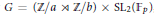 p )
p )
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 2 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 206-214
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation
NEW OBSTRUCTIONS FOR THE SURJECTIVITY OF THE JOHNSON HOMOMORPHISM OF THE AUTOMORPHISM GROUP OF A FREE GROUP
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 25 October 2006, pp. 341-360
- Print publication:
- October 2006
-
- Article
- Export citation
ARTINIAN-FINITARY GROUPS OVER COMMUTATIVE RINGS AND NON-COMMUTATIVE RINGS
-
- Journal:
- Journal of the London Mathematical Society / Volume 70 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 01 October 2004, pp. 325-340
- Print publication:
- October 2004
-
- Article
- Export citation
WHEN IS THE AUTOMORPHISM GROUP OF A VIRTUALLY POLYCYCLIC GROUP VIRTUALLY POLYCYCLIC?
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 10 September 2003, pp. 527-533
- Print publication:
- September 2003
-
- Article
-
- You have access
- Export citation
REGULAR-NILPOTENT GROUPS OF AUTOMORPHISMS
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 01 May 2003, pp. 1-5
- Print publication:
- January 2003
-
- Article
-
- You have access
- Export citation
Automorphisms of Metabelian Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-104
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation