No CrossRef data available.
Article contents
NON-TAME AUTOMORPHISMS OF A FREE GROUP OF RANK 3 IN 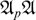
Published online by Cambridge University Press: 01 September 2007
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We give a way of constructing non-tame automorphisms of a free group of rank 3 in the variety 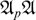 , with p prime.
, with p prime.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2007
References
REFERENCES
1.Adkins, W. A. and Weintraub, S. H., Algebra: an approach via module theory, Graduate Texts in Mathematics No. 136 (Springer-Verlag 1992).CrossRefGoogle Scholar
2.Bachmuth, S., Automorphisms of free metabelian groups, Trans. Amer. Math. Soc. 118 (1965), 93–104.CrossRefGoogle Scholar
3.Bachmuth, S., Automorphisms of a class of metabelian groups, Trans. Amer. Math. Soc. 127 (1967), 284–293.CrossRefGoogle Scholar
4.Bachmuth, S. and Mochizuki, H. Y., E 2 ≠ SL2 for most Laurent polynomial rings, Amer. J. Math. (6) 104 (1981), 1181–1189.CrossRefGoogle Scholar
5.Bachmuth, S. and Mochizuki, H. Y., The nonfinite generation of aut(G), G free metabelian of rank 3, Trans. Amer. Math. Soc. 270 (1982), 693–700.Google Scholar
6.Chein, O., IA-automorphisms of free and free metabelian groups, Comm. Pure Appl. Math. 21 (1968), 605–629.CrossRefGoogle Scholar
7.Gupta, N. D., Free group rings, Contemp. Math. No. 66 (American Mathematical Society 1987).CrossRefGoogle Scholar
8.Evans, M. J., Primitive elements in the free metabelian group of rank 3, J. Algebra 220 (1999), 475–491.CrossRefGoogle Scholar
9.Fox, R. H., Free differential calculus I, Annals of Math 57 (1953), 547–560.CrossRefGoogle Scholar
10.Hall, P., Finiteness conditions for soluble groups, Proc. London Math. Soc. (3) 4 (1954), 419–436.Google Scholar
11.Krasnikov, A. F., Nilpotent subgroups of relatively free groups, (Russian) Algebra i Logika (4) 17 (1978), 389–401; translation in Algebra and Logic (4) 17 (1978), 263–270.Google Scholar
12.Lidl, R. and Niederreiter, H., Finite fields, Encyclopedia of Mathematics and its Applications Vol. 20 (Addison-Wesley Publ. Company 1983).Google Scholar
13.Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory (Dover Publications, Inc., New York 1976).Google Scholar
15.Niven, I., Zuckerman, H. and Montgomery, H., An introduction to the theory of numbers, Fifth Edition (John Wiley & Sons, 1991).Google Scholar
16.Papistas, A. I., Automorphisms of metabelian groups, Canad. Math. Bull. 41 (1998), 98–104.CrossRefGoogle Scholar
17.Roman'kov, V. A., Primitive elements of free groups of rank 3, Math. Sb. 182 (1991), 1074–1085; (English transl.) Math. USSR-Sb. 73 (1992), 445–454.Google Scholar
18.Sehgal, S. K., Topics in group rings, Pure and Applied Mathematics, Vol. 50 (Marcel Dekker 1978).Google Scholar
20.Suslin, A. A., On the structure of the special linear group over polynomial rings, Izv. Akad. Nauk. 11 (1974), 221–238.Google Scholar

