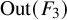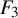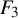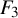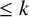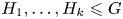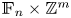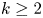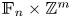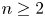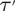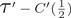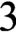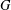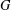Refine search
Actions for selected content:
33 results
The group of reversible turing machines: subgroups, generators, and computability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 October 2025, e176
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DYNAMICS OF ENDOMORPHISMS OF THE DIRECT PRODUCT OF TWO FREE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-23
-
- Article
- Export citation
The complexity of intersecting subproducts with subgroups in Cartesian powers
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 07 October 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALGORITHMICALLY FINITE, UNIVERSAL, AND
 $*$-UNIVERSAL GROUPS
$*$-UNIVERSAL GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Thompson groups for Ważewski dendrites
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 189-231
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The nonabelian product modulo sum
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1069-1109
-
- Article
- Export citation
The conjugacy problem for
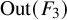 $\operatorname {Out}(F_3)$
$\operatorname {Out}(F_3)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Membership problems for positive one-relator groups and one-relation monoids
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective dynamical systems beyond dimension zero and factors of SFTs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1329-1369
- Print publication:
- May 2025
-
- Article
- Export citation
COMPUTING CENTRALISERS IN [FINITELY GENERATED FREE]-BY-CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 June 2024, pp. 118-127
- Print publication:
- February 2025
-
- Article
- Export citation
Finite skew braces of square-free order and supersolubility
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PRO-
 $\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
$\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 363-383
- Print publication:
- June 2024
-
- Article
- Export citation
Intersection configurations in free and free times free-abelian groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1552-1582
- Print publication:
- October 2024
-
- Article
- Export citation
Decidability problem for exponential equations in finitely presented groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 731-748
- Print publication:
- September 2023
-
- Article
- Export citation
Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 March 2021, pp. 545-566
- Print publication:
- June 2022
-
- Article
- Export citation
COMPUTABILITY, ORDERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1588-1598
- Print publication:
- December 2020
-
- Article
- Export citation
On commensurability of right-angled Artin groups II: RAAGs defined by paths
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 559-608
- Print publication:
- May 2021
-
- Article
- Export citation
ON THE RECOGNITION OF RIGHT-ANGLED ARTIN GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 19 June 2019, pp. 473-475
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
UNDECIDABILITY AND THE DEVELOPABILITY OF PERMUTOIDS AND RIGID PSEUDOGROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 20 March 2017, e10
-
- Article
-
- You have access
- Open access
- Export citation
THE FIRST-ORDER THEORY OF BRANCH GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 February 2016, pp. 150-158
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation