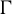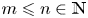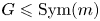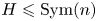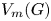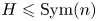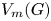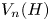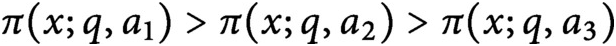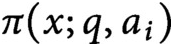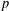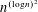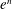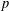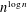Refine search
Actions for selected content:
16 results
Co-spectral radius of intersections
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 17 April 2023, pp. 509-523
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some embeddings between symmetric R. thompson groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 1-18
-
- Article
- Export citation
Densities in certain three-way prime number races
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
- Print publication:
- February 2022
-
- Article
- Export citation
BRANCH GROUPS, ORBIT GROWTH, AND SUBGROUP GROWTH TYPES FOR PRO-
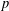 $p$ GROUPS
$p$ GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e10
-
- Article
-
- You have access
- Open access
- Export citation
CLASSIFICATION OF THE SUBLATTICES OF A LATTICE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 50-61
- Print publication:
- February 2021
-
- Article
- Export citation
Embedding right-angled Artin groups into Brin–Thompson groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 23 April 2019, pp. 225-229
- Print publication:
- September 2020
-
- Article
- Export citation
Centralizers in Houghton’s Groups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 3 / October 2015
- Published online by Cambridge University Press:
- 05 January 2015, pp. 769-785
-
- Article
-
- You have access
- Export citation
ON THE LOCAL-INDICABILITY COHEN–LYNDON THEOREM
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 637-656
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Surface groups within Baumslag doubles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 91-97
-
- Article
-
- You have access
- Export citation
THE DENSITY OF SUBGROUP INDICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 257-267
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
COUNTING SUBGROUPS IN A FAMILY OF NILPOTENT SEMI-DIRECT PRODUCTS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 5 / October 2006
- Published online by Cambridge University Press:
- 20 September 2006, pp. 743-752
- Print publication:
- October 2006
-
- Article
- Export citation
PROFINITE GROUPS WITH MULTIPLICATIVE PROBABILISTIC ZETA FUNCTION
-
- Journal:
- Journal of the London Mathematical Society / Volume 70 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 23 July 2004, pp. 165-181
- Print publication:
- August 2004
-
- Article
- Export citation
ON NON-CO-HOPFIAN P-GROUPS WITH FINITE DERIVED SUBGROUP
-
- Journal:
- Glasgow Mathematical Journal / Volume 46 / Issue 2 / May 2004
- Published online by Cambridge University Press:
- 19 May 2004, pp. 363-369
- Print publication:
- May 2004
-
- Article
-
- You have access
- Export citation
THE CARTER SUBGROUPS OF SOME CLASSICAL GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 02 February 2004, pp. 145-155
- Print publication:
- March 2004
-
- Article
- Export citation
Amalgamated Products and the Howson Property
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 3 / 01 September 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 330-340
- Print publication:
- 01 September 1997
-
- Article
-
- You have access
- Export citation
Remarks on the Intersection of Finitely Generated Subgroups of a Free Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 2 / 01 June 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 204-207
- Print publication:
- 01 June 1986
-
- Article
-
- You have access
- Export citation