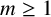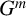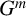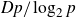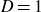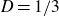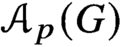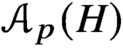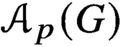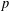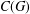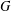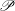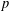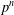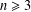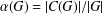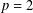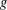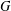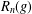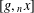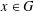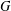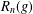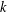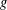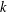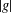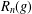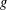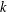Refine search
Actions for selected content:
17 results
GROUPS HAVING 12 CYCLIC SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-12
-
- Article
- Export citation
On finite groups with bounded conjugacy classes of commutators
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-6
-
- Article
- Export citation
ON THE LARGEST CHARACTER DEGREE OF SOLVABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH FEW NONPOWER SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 10 August 2023, pp. 529-540
- Print publication:
- June 2024
-
- Article
- Export citation
Prime divisors and the number of conjugacy classes of finite groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-16
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-GROUPS WITH CYCLIC OR GENERALISED QUATERNION HUGHES SUBGROUPS: CLASSIFYING TIDY p-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 443-448
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH A GIVEN NUMBER OF NONPOWER SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 315-319
- Print publication:
- October 2022
-
- Article
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
THE SECOND MINIMUM/MAXIMUM VALUE OF THE NUMBER OF CYCLIC SUBGROUPS OF FINITE
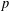 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 April 2020, pp. 96-103
- Print publication:
- February 2021
-
- Article
- Export citation
RIGHT ENGEL-TYPE SUBGROUPS AND LENGTH PARAMETERS OF FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 340-350
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
FINITE GROUPS WITH SOME WEAKLY S-SUPPLEMENTED SUBGROUPS
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 2 / May 2011
- Published online by Cambridge University Press:
- 08 December 2010, pp. 211-222
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
MULTIPLICITIES IN SYLOW SEQUENCES AND THE SOLVABLE RADICAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 477-486
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
SCHREIER CONDITIONS ON CHIEF FACTORS AND RESIDUALS OF SOLVABLE-LIKE GROUP FORMATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 97-106
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Finite group with Hall coverings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-16
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
THE CARTER SUBGROUPS OF SOME CLASSICAL GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 02 February 2004, pp. 145-155
- Print publication:
- March 2004
-
- Article
- Export citation
Coverings and coverings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-128
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
On Supersolvable Groups and a Theorem of Huppert
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 3 / 01 September 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 314-315
- Print publication:
- 01 September 1990
-
- Article
-
- You have access
- Export citation