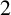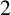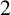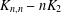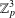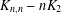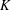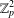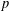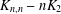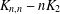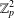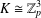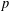This paper contributes to the regular covers of a complete bipartite graph minus a matching, denoted 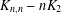 $K_{n,n}-nK_{2}$ , whose fiber-preserving automorphism group acts 2-arc-transitively. All such covers, when the covering transformation group
$K_{n,n}-nK_{2}$ , whose fiber-preserving automorphism group acts 2-arc-transitively. All such covers, when the covering transformation group 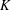 $K$ is either cyclic or
$K$ is either cyclic or 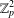 $\mathbb{Z}_{p}^{2}$ with
$\mathbb{Z}_{p}^{2}$ with 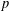 $p$ a prime, have been determined in Xu and Du [‘2-arc-transitive cyclic covers of
$p$ a prime, have been determined in Xu and Du [‘2-arc-transitive cyclic covers of 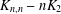 $K_{n,n}-nK_{2}$ ’, J. Algebraic Combin.39 (2014), 883–902] and Xu et al. [‘2-arc-transitive regular covers of
$K_{n,n}-nK_{2}$ ’, J. Algebraic Combin.39 (2014), 883–902] and Xu et al. [‘2-arc-transitive regular covers of 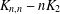 $K_{n,n}-nK_{2}$ with the covering transformation group
$K_{n,n}-nK_{2}$ with the covering transformation group 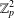 $\mathbb{Z}_{p}^{2}$ ’, Ars. Math. Contemp.10 (2016), 269–280]. Finally, this paper gives a classification of all such covers for
$\mathbb{Z}_{p}^{2}$ ’, Ars. Math. Contemp.10 (2016), 269–280]. Finally, this paper gives a classification of all such covers for 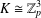 $K\cong \mathbb{Z}_{p}^{3}$ with
$K\cong \mathbb{Z}_{p}^{3}$ with 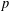 $p$ a prime.
$p$ a prime.
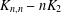 $K_{n,n}-nK_{2}$ HAVING THE COVERING TRANSFORMATION GROUP
$K_{n,n}-nK_{2}$ HAVING THE COVERING TRANSFORMATION GROUP 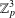 $\mathbb{Z}_{p}^{3}$
$\mathbb{Z}_{p}^{3}$