We demonstrate how exact structures can be placed on the additive category of right operator modules over an operator algebra in order to discuss global dimension for operator algebras. The properties of the Haagerup tensor product play a decisive role in this.

We show that the Schur multiplier of a Noetherian group need not be finitely generated. We prove that the non-abelian tensor product of a polycyclic (resp. polycyclic-by-finite) group and a Noetherian group is a polycyclic (resp. polycyclic-by-finite) group. We also prove new versions of Schur's theorem.

We analyse infinitesimal deformations of pairs $(X,{\mathcal{F}})$ with ${\mathcal{F}}$ a coherent sheaf on a smooth projective variety $X$ over an algebraically closed field of characteristic 0. We describe a differential graded Lie algebra controlling the deformation problem, and we prove an analog of a Mukai–Artamkin theorem about the trace map.

The main difficulty in the theory of non-abelian cohomology is that for cosimplicial groups only zero-th and first dimensional cohomotopy are known. In this article we introduce a new class of cosimplicial groups, called centralised cosimplicial groups, for which we are able to define a second cohomotopy, with all expected properties. The main examples of such cosimplicial groups come from 2-categories.

This paper gives a characterization of homotopy fibres of inverse image maps on groupoids of torsors that are induced by geometric morphisms, in terms of both pointed torsors and pointed cocycles, suitably defined. Cocycle techniques are used to give a complete description of such fibres, when the underlying geometric morphism is the canonical stalk on the classifying topos of a profinite group $G$. If the torsors in question are defined with respect to a constant group $H$, then the path components of the fibre can be identified with the set of continuous maps from the profinite group $G$ to the group $H$. More generally, when $H$ is not constant, this set of path components is the set of continuous maps from a pro-object in sheaves of groupoids to $H$, which pro-object can be viewed as a “Grothendieck fundamental groupoid”.

Non-abelian homology of Lie algebras with coefficients in Lie algebras is constructed and studied, generalising the classical Chevalley-Eilenberg homology of Lie algebras. The relationship between cyclic homology and Milnor cyclic homology of non-commutative associative algebras is established in terms of the long exact non-abelian homology sequence of Lie algebras. Some explicit formulae for the second and the third non-abelian homology of Lie algebras are obtained.

Certain canonical resolutions are described for free associative and free Lie algebras in the category of non-associative algebras. These resolutions derive in both cases from geometric objects, which in turn reflect the combinatorics of suitable collections of leaf-labeled trees.

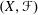
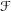
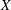
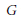
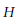
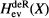In [Con2] Connes introduced cyclic cohomology HC*(A) for an associative algebra A. When A is a complex algebra he constructed a Chern character for p-summable Fredholm modules over A taking values in HC*(A). As a very special case, when X is a closed C∞-manifold and A = C∞ (X), this construction recovers the usual Chern character, which is a rational isomorphism from the K-homology K0(X) to , the even dimensional deRham homology of X.

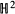The general problem of what should be a non-abelian cohomology, what is it supposed to do, and what should be the coefficients, form a set of interesting questions which has been around for a long time. In the particular setting of groups, a comprehensible and well motivated cohomology theory has been so far stated in dimensions ≤ 2, the coefficients for being crossed modules. The main effort to define an appropriate for groups has been done by Dedecker [16] and Van Deuren [40]; they studied the obstruction to lifting non-abelian 2-cocycles and concluded with first approach for , which requires “super crossed groups” as coefficients. However, as Dedecker said “some polishing work remains necessary” for his cohomology.