Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bullejos, M.
Carrasco, P.
and
Cegarra, A. M.
1993.
Cohomology with coefficients in symmetric cat-groups. An extension of Eilenberg–MacLane's classification theorem.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 114,
Issue. 1,
p.
163.
Ellis, Graham
and
Hardie, Keith
1995.
A projective homotopy theory of crossedG-modules.
Applied Categorical Structures,
Vol. 3,
Issue. 3,
p.
201.
Cabello, Julia G.
and
Garzón, Antonio R.
1995.
Closed model structures for algebraic models of n-types.
Journal of Pure and Applied Algebra,
Vol. 103,
Issue. 3,
p.
287.
Carrasco, P.
and
Cegarra, A.M.
1996.
Schreier theory for central extensions of categorical groups1.
Communications in Algebra,
Vol. 24,
Issue. 13,
p.
4059.
Carrasco, P.
and
Cegarra, A.M.
1996.
(Braided) tensor structures on homotopy groupoids and nerves of (Braided) categorical groups1.
Communications in Algebra,
Vol. 24,
Issue. 13,
p.
3995.
Ellis, Graham
1998.
On Peiffer central series.
Glasgow Mathematical Journal,
Vol. 40,
Issue. 2,
p.
177.
Carrasco, Pilar
Garzón, Antonio R.
and
Miranda, Jesús G.
2000.
Schreier theory for singular extensions of categorical groups and homotopy classification∗∗.
Communications in Algebra,
Vol. 28,
Issue. 5,
p.
2585.
Cegarra, Antonio M.
and
Garzón, Antonio R.
2001.
Homotopy Classification of Categorical Torsors.
Applied Categorical Structures,
Vol. 9,
Issue. 5,
p.
465.
Vitale, Enrico M.
2002.
A Picard–Brauer exact sequence of categorical groups.
Journal of Pure and Applied Algebra,
Vol. 175,
Issue. 1-3,
p.
383.
Garzón, A.R.
Inassaridze, H.
and
Río, A. del
2004.
Derivations of categorical groups.
Theory and Applications of Categories,
Vol. 13,
Issue. ,
p.
86.
Blanco, V.
Bullejos, M.
and
Faro, E.
2005.
Categorical non-abelian cohomology and the Schreier theory of groupoids.
Mathematische Zeitschrift,
Vol. 251,
Issue. 1,
p.
41.
Garzón, Antonio R.
and
del Río, Aurora
2006.
On ℋ1 of Categorical Groups.
Communications in Algebra,
Vol. 34,
Issue. 10,
p.
3691.
Muro, Fernando
and
Tonks, Andrew
2007.
The 1-type of a Waldhausen K-theory spectrum.
Advances in Mathematics,
Vol. 216,
Issue. 1,
p.
178.
Baues, Hans-Joachim
and
Muro, Fernando
2008.
Secondary homotopy groups.
Forum Mathematicum,
Vol. 20,
Issue. 4,
Casas, José Manuel
Khmaladze, Emzar
and
Ladra, Manuel
2011.
Low-dimensional non-abelian Leibniz cohomology.
Forum Mathematicum,
p.
-.
Inassaridze, N.
2016.
Some Aspects of Homotopic Algebra and Non-Abelian (CO)Homology Theories.
Journal of Mathematical Sciences,
Vol. 213,
Issue. 1,
p.
1.
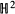 being crossed modules. The main effort to define an appropriate
being crossed modules. The main effort to define an appropriate 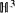 for groups has been done by Dedecker [16] and Van Deuren [40]; they studied the obstruction to lifting non-abelian 2-cocycles and concluded with first approach for
for groups has been done by Dedecker [16] and Van Deuren [40]; they studied the obstruction to lifting non-abelian 2-cocycles and concluded with first approach for 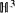 , which requires “super crossed groups” as coefficients. However, as Dedecker said “some polishing work remains necessary” for his cohomology.
, which requires “super crossed groups” as coefficients. However, as Dedecker said “some polishing work remains necessary” for his cohomology.
