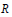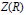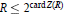Refine search
Actions for selected content:
4 results
WHEN IS A COMPLETION OF THE UNIVERSAL ENVELOPING ALGEBRA A BANACH PI-ALGEBRA?
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 493-501
- Print publication:
- June 2023
-
- Article
- Export citation
DEFORMATION CONDITIONS FOR PSEUDOREPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 18 July 2019, e20
-
- Article
-
- You have access
- Open access
- Export citation
STABLE JACOBSON RADICALS AND SEMIPRIME SMASH PRODUCTS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 6 / December 2005
- Published online by Cambridge University Press:
- 12 December 2005, pp. 860-872
- Print publication:
- December 2005
-
- Article
- Export citation
The Cardinality of the Center of a PI Ring
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-85
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation