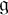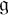Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aristov, Oleg Yu.
2023.
Length functions exponentially distorted on subgroups of complex Lie groups.
European Journal of Mathematics,
Vol. 9,
Issue. 3,