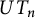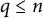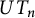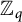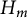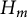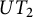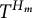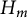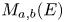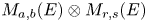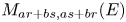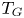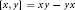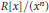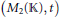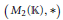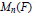Refine search
Actions for selected content:
15 results
On the central exponent of superalgebras with superinvolution
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 September 2025, pp. 1-18
-
- Article
- Export citation
On rings which are sums of subrings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 874-882
- Print publication:
- September 2025
-
- Article
- Export citation
Images of multilinear graded polynomials on upper triangular matrix algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1540-1565
- Print publication:
- October 2023
-
- Article
- Export citation
Specht property for the algebra of upper triangular matrices of size two with a Taft’s algebra action
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 16 May 2022, pp. 303-323
- Print publication:
- March 2023
-
- Article
- Export citation
Graded identities for algebras with elementary gradings over an infinite field
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 146-166
-
- Article
- Export citation
ODD–EVEN DECOMPOSITION OF FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 104-108
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
On Automorphisms and Commutativity in Semiprime Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 584-592
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
LIE METABELIAN SKEW ELEMENTS IN GROUP RINGS
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 13 August 2013, pp. 187-195
- Print publication:
- January 2014
-
- Article
-
- You have access
- Export citation
On the Existence of the Graded Exponent for Finite Dimensional ℤp -graded Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 2 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 271-284
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation
Extensions of Rings Having McCoy Condition
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 2 / 01 June 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 267-272
- Print publication:
- 01 June 2009
-
- Article
-
- You have access
- Export citation
Generalized Commutativity in Group Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 1 / 01 March 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 14-25
- Print publication:
- 01 March 2003
-
- Article
-
- You have access
- Export citation
 $*$ -Subvarieties of the Variety Generated by
$*$ -Subvarieties of the Variety Generated by 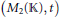 $\left( {{M}_{2}}\left( \mathbb{K} \right),\,t \right)$
$\left( {{M}_{2}}\left( \mathbb{K} \right),\,t \right)$
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 1 / 01 February 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 42-63
- Print publication:
- 01 February 2003
-
- Article
-
- You have access
- Export citation
On Permanental Identities of Symmetric and Skew-Symmetric Matrices in Characteristic p
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 118-124
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation
Central *-Differential Identities in Prime Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 2 / 01 June 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 211-215
- Print publication:
- 01 June 1996
-
- Article
-
- You have access
- Export citation
Cocharacters, Codimensions and Hilbert Series of the Polynomial Identities for 2 × 2 Matrices with Involution
-
- Journal:
- Canadian Journal of Mathematics / Volume 46 / Issue 4 / 01 August 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 718-733
- Print publication:
- 01 August 1994
-
- Article
-
- You have access
- Export citation