No CrossRef data available.
Article contents
On Permanental Identities of Symmetric and Skew-Symmetric Matrices in Characteristic p
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 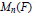 ${{M}_{n}}(F)$ be the algebra of
${{M}_{n}}(F)$ be the algebra of 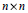 $n\times n$ matrices over a field
$n\times n$ matrices over a field 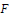 $F$ of characteristic
$F$ of characteristic 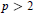 $p>2$ and let
$p>2$ and let 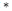 $*$ be an involution on
$*$ be an involution on 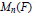 ${{M}_{n}}(F)$ . If
${{M}_{n}}(F)$ . If 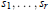 ${{s}_{1}},...,{{s}_{r}}$ are symmetric variables we determine the smallest
${{s}_{1}},...,{{s}_{r}}$ are symmetric variables we determine the smallest  $r$ such that the polynomial
$r$ such that the polynomial
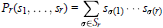 $${{P}_{r}}({{S}_{1}},...,{{S}_{r}})\,=\,\sum\limits_{\sigma \in {{S}_{r}}}{{{S}_{\sigma (1)}}...{{S}_{\sigma (r)}}}$$
$${{P}_{r}}({{S}_{1}},...,{{S}_{r}})\,=\,\sum\limits_{\sigma \in {{S}_{r}}}{{{S}_{\sigma (1)}}...{{S}_{\sigma (r)}}}$$
is a  $*$ -polynomial identity of
$*$ -polynomial identity of 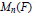 ${{M}_{n}}(F)$ under either the symplectic or the transpose involution. We also prove an analogous result for the polynomial
${{M}_{n}}(F)$ under either the symplectic or the transpose involution. We also prove an analogous result for the polynomial
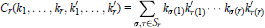 $${{C}_{r}}\left( {{k}_{1}},...,{{k}_{r,}}{{{{k}'}}_{1}},...,{{{{k}'}}_{r}} \right)=\sum\limits_{\sigma ,\tau \in {{S}_{r}}}{{{k}_{\sigma \left( 1 \right)}}{{{{k}'}}_{\tau \left( 1 \right)}}\cdot \cdot \cdot {{k}_{\sigma \left( r \right)}}{{{{k}'}}_{\tau \left( r \right)}}}$$
$${{C}_{r}}\left( {{k}_{1}},...,{{k}_{r,}}{{{{k}'}}_{1}},...,{{{{k}'}}_{r}} \right)=\sum\limits_{\sigma ,\tau \in {{S}_{r}}}{{{k}_{\sigma \left( 1 \right)}}{{{{k}'}}_{\tau \left( 1 \right)}}\cdot \cdot \cdot {{k}_{\sigma \left( r \right)}}{{{{k}'}}_{\tau \left( r \right)}}}$$
where 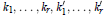 ${{k}_{1}},...,{{k}_{r}},k_{1}^{'},...,k_{r}^{'}$ are skew variables under the transpose involution.
${{k}_{1}},...,{{k}_{r}},k_{1}^{'},...,k_{r}^{'}$ are skew variables under the transpose involution.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998

