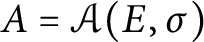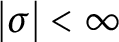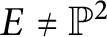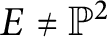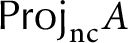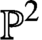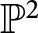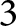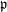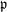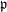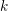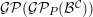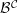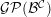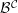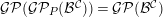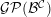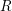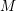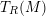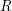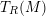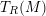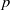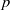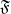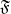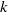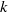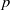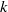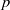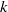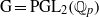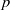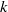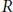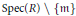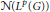Refine search
Actions for selected content:
21 results
Model structures, n-Gorenstein flat modules and PGF dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1241-1264
-
- Article
- Export citation
Quantum projective planes finite over their centers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 53-67
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cut cotorsion pairs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 548-585
- Print publication:
- September 2022
-
- Article
- Export citation
AS-REGULARITY OF GEOMETRIC ALGEBRAS OF PLANE CUBIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 193-217
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
GRADED TWISTED CALABI–YAU ALGEBRAS ARE GENERALIZED ARTIN–SCHELTER REGULAR
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 100-153
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Complete Classification of 3-dimensional Quadratic AS-regular Algebras of Type EC
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 123-141
- Print publication:
- March 2021
-
- Article
- Export citation
LOCAL DUALITY FOR THE SINGULARITY CATEGORY OF A FINITE DIMENSIONAL GORENSTEIN ALGEBRA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 1-24
- Print publication:
- December 2021
-
- Article
- Export citation
GORENSTEIN PROJECTIVE OBJECTS IN FUNCTOR CATEGORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 1-41
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
The Gorenstein-projective modules over a monomial algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 02 October 2018, pp. 1115-1134
- Print publication:
- December 2018
-
- Article
- Export citation
GORENSTEIN HOMOLOGICAL PROPERTIES OF TENSOR RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 07 June 2018, pp. 188-208
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
NON-AFFINE HOPF ALGEBRA DOMAINS OF GELFAND–KIRILLOV DIMENSION TWO
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 563-593
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
REGULARITY CRITERION AND CLASSIFICATION FOR ALGEBRAS OF JORDAN TYPE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 69-95
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
On the Generalized Auslander–Reiten Conjecture under Certain Ring Extensions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 1 / 01 March 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 134-143
- Print publication:
- 01 March 2015
-
- Article
-
- You have access
- Export citation
Pro-
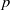 $\lowercase p$ Iwahori–Hecke algebras are Gorenstein
$\lowercase p$ Iwahori–Hecke algebras are Gorenstein
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 28 November 2013, pp. 753-809
- Print publication:
- October 2014
-
- Article
- Export citation
NOETHERIAN HOPF ALGEBRAS
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue A / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 75-87
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
GRADED MORITA EQUIVALENCES FOR GEOMETRIC AS-REGULAR ALGEBRAS
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 241-257
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation
Finite Cohen–Macaulay Type and Smooth Non-Commutative Schemes
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 2 / 01 April 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 379-390
- Print publication:
- 01 April 2008
-
- Article
-
- You have access
- Export citation
CO-POINT MODULES OVER KOSZUL ALGEBRAS
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 04 January 2007, pp. 639-656
- Print publication:
- December 2006
-
- Article
- Export citation
Auslander–Reiten sequences, locally free sheaves and Chebysheff polynomials
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 13 March 2006, pp. 397-408
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Biprojectivity and Biflatness for Convolution Algebras of Nuclear Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 3 / 01 September 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 445-455
- Print publication:
- 01 September 2004
-
- Article
-
- You have access
- Export citation





 . The homotopy category of this model structure is triangulated equivalent to the stable category
. The homotopy category of this model structure is triangulated equivalent to the stable category