Article contents
Pro-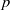 $\lowercase p$ Iwahori–Hecke algebras are Gorenstein
$\lowercase p$ Iwahori–Hecke algebras are Gorenstein
Published online by Cambridge University Press: 28 November 2013
Abstract
Let 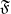 $\mathfrak{F}$ be a locally compact nonarchimedean field with residue characteristic
$\mathfrak{F}$ be a locally compact nonarchimedean field with residue characteristic 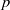 $p$, and let
$p$, and let 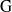 $\mathrm{G} $ be the group of
$\mathrm{G} $ be the group of 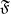 $\mathfrak{F}$-rational points of a connected split reductive group over
$\mathfrak{F}$-rational points of a connected split reductive group over 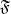 $\mathfrak{F}$. For
$\mathfrak{F}$. For  $k$ an arbitrary field of any characteristic, we study the homological properties of the Iwahori–Hecke
$k$ an arbitrary field of any characteristic, we study the homological properties of the Iwahori–Hecke 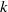 $k$-algebra
$k$-algebra  ${\mathrm{H} }^{\prime } $ and of the pro-
${\mathrm{H} }^{\prime } $ and of the pro-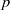 $p$ Iwahori–Hecke
$p$ Iwahori–Hecke 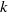 $k$-algebra
$k$-algebra 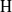 $\mathrm{H} $ of
$\mathrm{H} $ of 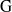 $\mathrm{G} $. We prove that both of these algebras are Gorenstein rings with self-injective dimension bounded above by the rank of
$\mathrm{G} $. We prove that both of these algebras are Gorenstein rings with self-injective dimension bounded above by the rank of 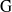 $\mathrm{G} $. If
$\mathrm{G} $. If 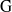 $\mathrm{G} $ is semisimple, we also show that this upper bound is sharp, that both
$\mathrm{G} $ is semisimple, we also show that this upper bound is sharp, that both 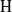 $\mathrm{H} $ and
$\mathrm{H} $ and 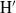 ${\mathrm{H} }^{\prime } $ are Auslander–Gorenstein, and that there is a duality functor on the finite length modules of
${\mathrm{H} }^{\prime } $ are Auslander–Gorenstein, and that there is a duality functor on the finite length modules of 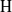 $\mathrm{H} $ (respectively
$\mathrm{H} $ (respectively 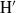 ${\mathrm{H} }^{\prime } $). We obtain the analogous Gorenstein and Auslander–Gorenstein properties for the graded rings associated to
${\mathrm{H} }^{\prime } $). We obtain the analogous Gorenstein and Auslander–Gorenstein properties for the graded rings associated to 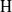 $\mathrm{H} $ and
$\mathrm{H} $ and 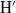 ${\mathrm{H} }^{\prime } $.
${\mathrm{H} }^{\prime } $.
When 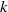 $k$ has characteristic
$k$ has characteristic 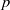 $p$, we prove that in ‘most’ cases
$p$, we prove that in ‘most’ cases 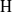 $\mathrm{H} $ and
$\mathrm{H} $ and 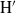 ${\mathrm{H} }^{\prime } $ have infinite global dimension. In particular, we deduce that the category of smooth
${\mathrm{H} }^{\prime } $ have infinite global dimension. In particular, we deduce that the category of smooth 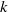 $k$-representations of
$k$-representations of 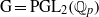 $\mathrm{G} = {\mathrm{PGL} }_{2} ({ \mathbb{Q} }_{p} )$ generated by their invariant vectors under the pro-
$\mathrm{G} = {\mathrm{PGL} }_{2} ({ \mathbb{Q} }_{p} )$ generated by their invariant vectors under the pro-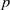 $p$ Iwahori subgroup has infinite global dimension (at least if
$p$ Iwahori subgroup has infinite global dimension (at least if 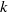 $k$ is algebraically closed).
$k$ is algebraically closed).
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 4 , October 2014 , pp. 753 - 809
- Copyright
- ©Cambridge University Press 2013
References
- 11
- Cited by

