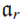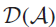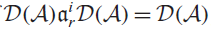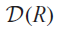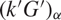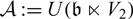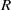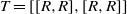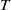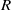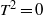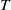Refine search
Actions for selected content:
17 results
GRAPH CHARACTERISATION OF THE ANNIHILATOR IDEALS OF LEAVITT PATH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 498-507
- Print publication:
- December 2024
-
- Article
- Export citation
EVERY GRADED IDEAL OF A LEAVITT PATH ALGEBRA IS GRADED ISOMORPHIC TO A LEAVITT PATH ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 August 2021, pp. 248-256
- Print publication:
- April 2022
-
- Article
- Export citation
SIMPLICITY CRITERIA FOR RINGS OF DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 347-351
- Print publication:
- May 2022
-
- Article
- Export citation
Maximal prime homomorphic images of mod-p Iwasawa algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 05 March 2021, pp. 387-419
- Print publication:
- September 2021
-
- Article
- Export citation
COMPLETELY PRIME ONE-SIDED IDEALS IN SKEW POLYNOMIAL RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 03 February 2021, pp. 114-121
- Print publication:
- January 2022
-
- Article
- Export citation
THE PRIME IDEALS AND SIMPLE MODULES OF THE UNIVERSAL ENVELOPING ALGEBRA U(𝔟⋉V2)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. S77-S98
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
On Annelidan, Distributive, and Bézout Rings
- Part of
- Modules, bimodules and ideals
- Chain conditions, growth conditions, and other forms of finiteness
- Boolean algebras (Boolean rings)
- Distributive lattices
- Local rings and generalizations
- Radicals and radical properties of rings
- Conditions on elements
- Rings and algebras arising under various constructions
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1082-1110
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
On a Theorem of Burgess and Stephenson
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 06 December 2018, pp. 603-605
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
The Universal Enveloping Algebra of the Schrödinger Algebra and its Prime Spectrum
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 688-703
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
GRADED CHAIN CONDITIONS AND LEAVITT PATH ALGEBRAS OF NO-EXIT GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 December 2017, pp. 229-256
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
FINITE HIGHER COMMUTATORS IN ASSOCIATIVE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 September 2013, pp. 503-509
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
REAL IDEALS IN POINTFREE RINGS OF CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 338-352
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
ON RINGS WHOSE RIGHT ANNIHILATORS ARE BOUNDED
-
- Journal:
- Glasgow Mathematical Journal / Volume 51 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 September 2009, pp. 539-559
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
ON NONCOMMUTATIVE VNL-RINGS AND GVNL-RINGS
-
- Journal:
- Glasgow Mathematical Journal / Volume 48 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 24 March 2006, pp. 11-17
- Print publication:
- January 2006
-
- Article
-
- You have access
- Export citation
Essential ideals of incidence algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 252-260
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
The J0 -Radical of a Matrix Nearring can be Intermediate
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 2 / 01 June 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 198-203
- Print publication:
- 01 June 1997
-
- Article
-
- You have access
- Export citation
Stably Free Modules Over Rings of Generalised Integer Quaternions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 4 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 408-411
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation