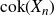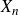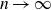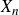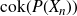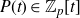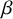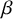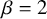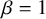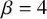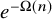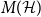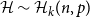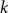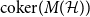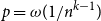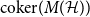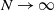Refine search
Actions for selected content:
24 results
A central limit theorem for partial transposes of multipartite Wishart matrices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-38
-
- Article
-
- You have access
- HTML
- Export citation
Integration on complex Grassmannians, deformed monotone Hurwitz numbers, and interlacing phenomena
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moments of the free Jacobi process: A matrix approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 966-991
- Print publication:
- September 2025
-
- Article
- Export citation
The cokernel of a polynomial push-forward of a random integral matrix with concentrated residue
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 229-257
- Print publication:
- March 2025
-
- Article
- Export citation
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The full rank condition for sparse random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 643-707
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting elements of the congruence subgroup
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 955-969
- Print publication:
- December 2024
-
- Article
- Export citation
Asymptotic expansion of
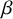 $\beta $ matrix models in the multi-cut regime
$\beta $ matrix models in the multi-cut regime
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 24 January 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The least singular value of a random symmetric matrix
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Autocorrelations of characteristic polynomials for the Alternative Circular Unitary Ensemble
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 51-64
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian groups from random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 654-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RECURSIVE CHARACTERISATIONS OF RANDOM MATRIX ENSEMBLES AND ASSOCIATED COMBINATORIAL OBJECTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 342-343
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Rank-uniform local law for Wigner matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 October 2022, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the moments of characteristic polynomials
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 05 August 2022, pp. S102-S122
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random symmetric matrices: rank distribution and irreducibility of the characteristic polynomial
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 May 2022, pp. 233-246
- Print publication:
- March 2023
-
- Article
- Export citation
Matrix Liberation Process II: Relation to Orbital Free Entropy
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 493-541
- Print publication:
- April 2021
-
- Article
- Export citation
Surjectivity of near-square random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 06 November 2019, pp. 267-292
-
- Article
- Export citation
Freeness and The Partial Transposes of Wishart Random Matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 659-681
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Fluctuation of Matrix Entries and Application to Outliers of Elliptic Matrices
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-25
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
Computing the Smallest Eigenvalue of Large Ill-Conditioned Hankel Matrices
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 104-124
- Print publication:
- July 2015
-
- Article
- Export citation