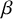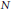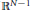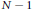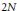Refine search
Actions for selected content:
10 results
The extremal landscape for the C
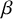 $\beta $E ensemble
$\beta $E ensemble
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 January 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the simulation of the Ginibre point process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1003-1012
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Free Bessel Laws
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 1 / 01 February 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-37
- Print publication:
- 01 February 2011
-
- Article
-
- You have access
- Export citation
Conjugate Reciprocal Polynomials with All Roots on the Unit Circle
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 5 / October 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1149-1167
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
On the Relation Between the Gaussian Orthogonal Ensemble and Reflections, or a Self-Adjoint Version of the Marcus–Pisier Inequality
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 2 / 01 June 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-320
- Print publication:
- 01 June 2006
-
- Article
-
- You have access
- Export citation
Integral moments of L-functions
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 22 June 2005, pp. 33-104
- Print publication:
- July 2005
-
- Article
- Export citation
Application of the τ-function theory of Painlevé equations to random matrices: PVI , the JUE, CyUE, cJUE and scaled limits
-
- Journal:
- Nagoya Mathematical Journal / Volume 174 / 2004
- Published online by Cambridge University Press:
- 22 January 2016, pp. 29-114
- Print publication:
- 2004
-
- Article
-
- You have access
- Export citation
Sparse random matrices: spectral edge and statistics of rooted trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 124-140
- Print publication:
- March 2001
-
- Article
- Export citation
Maps in Locally Orientable Surfaces and Integrals Over Real Symmetric Surfaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 5 / 01 October 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 865-882
- Print publication:
- 01 October 1997
-
- Article
-
- You have access
- Export citation
On the eigenvalues of random matrices
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 05 September 2017, pp. 49-62
- Print publication:
- 1994
-
- Article
-
- You have access
- Export citation