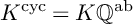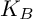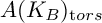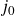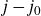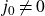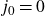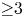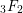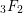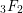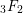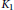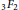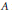Refine search
Actions for selected content:
12 results
A classification of Shimura curves in
 $ \mathscr {A}_g$
$ \mathscr {A}_g$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ESSENTIAL TORSION FINITENESS OF ABELIAN VARIETIES OVER TORSION FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 91-127
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complex multiplication and Noether–Lefschetz loci of the twistor space of a K3 surface
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 17-38
- Print publication:
- January 2024
-
- Article
- Export citation
Effective bounds on differences of singular moduli that are S-units
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 415-450
- Print publication:
- March 2023
-
- Article
- Export citation
Rigid-analytic varieties with projective reduction violating Hodge symmetry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 625-640
- Print publication:
- March 2021
-
- Article
- Export citation
CLASS NUMBERS OF CM ALGEBRAIC TORI, CM ABELIAN VARIETIES AND COMPONENTS OF UNITARY SHIMURA VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 28 October 2020, pp. 74-99
- Print publication:
- March 2022
-
- Article
- Export citation
Primes Dividing Invariants of CM Picard Curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 480-504
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
A FUNCTIONAL LOGARITHMIC FORMULA FOR THE HYPERGEOMETRIC FUNCTION
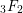 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 29-46
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
AN ALGEBRO-GEOMETRIC STUDY OF SPECIAL VALUES OF HYPERGEOMETRIC FUNCTIONS
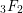 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 13 September 2018, pp. 47-62
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
CM Periods, CM Regulators, and Hypergeometric Functions, I
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 3 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-514
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
Tate Cycles on Abelian Varieties with Complex Multiplication
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 1 / 01 February 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 198-213
- Print publication:
- 01 February 2015
-
- Article
-
- You have access
- Export citation
The Chowla–Selberg Formula and The Colmez Conjecture
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 2 / 01 April 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 456-472
- Print publication:
- 01 April 2010
-
- Article
-
- You have access
- Export citation