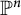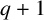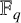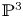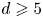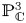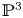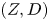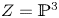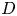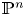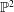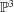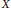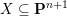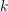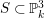Refine search
Actions for selected content:
20 results
On the irreducibility of Hessian loci of cubic hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological and motivic inclusion–exclusion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2228-2283
- Print publication:
- September 2024
-
- Article
- Export citation
On the moduli of hypersurfaces in toric orbifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 14 March 2024, pp. 577-616
-
- Article
- Export citation
Toric degenerations of low-degree hypersurfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1231-1236
- Print publication:
- December 2023
-
- Article
- Export citation
SMOOTHNESS IN PENCILS OF HYPERSURFACES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 85-94
- Print publication:
- February 2023
-
- Article
- Export citation
Moduli of surfaces in
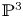 ${{\mathbb {P}}}^{3}$
${{\mathbb {P}}}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 1329-1374
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schiffer variations and the generic Torelli theorem for hypersurfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 89-122
- Print publication:
- January 2022
-
- Article
- Export citation
UNIRATIONALITY AND GEOMETRIC UNIRATIONALITY FOR HYPERSURFACES IN POSITIVE CHARACTERISTICS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 1831-1847
- Print publication:
- September 2022
-
- Article
- Export citation
Rational lines on cubic hypersurfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 99-112
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
On Homogeneous Polynomials Determined by their Partial Derivatives
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 06 December 2019, pp. 358-365
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
On Algebraic Surfaces Associated with Line Arrangements
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 471-499
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Twisted Alexander invariants of complex hypersurface complements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 1049-1073
- Print publication:
- October 2018
-
- Article
- Export citation
A Module-theoretic Characterization of Algebraic Hypersurfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 166-173
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
Measures of irrationality for hypersurfaces of large degree
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 04 September 2017, pp. 2368-2393
- Print publication:
- November 2017
-
- Article
- Export citation
AT MOST 64 LINES ON SMOOTH QUARTIC SURFACES (CHARACTERISTIC 2)
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 31 May 2017, pp. 76-95
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
Algebraic Cycles on Quadric Sections of Cubics in ℙ4 under the Action of Symplectomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 14 July 2015, pp. 377-392
-
- Article
- Export citation
On fibrations whose geometric fibers are nonreduced
-
- Journal:
- Nagoya Mathematical Journal / Volume 200 / December 2010
- Published online by Cambridge University Press:
- 11 January 2016, pp. 35-57
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Nonrational Weighted Hypersurfaces
-
- Journal:
- Nagoya Mathematical Journal / Volume 194 / 2009
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-32
- Print publication:
- 2009
-
- Article
-
- You have access
- Export citation
Logarithmic Vector Fields and Hyperbolicity
-
- Journal:
- Nagoya Mathematical Journal / Volume 195 / 2009
- Published online by Cambridge University Press:
- 11 January 2016, pp. 21-40
- Print publication:
- 2009
-
- Article
-
- You have access
- Export citation
DESSINS D'ENFANTS AND HYPERSURFACES WITH MANY $A_j$-SINGULARITIES
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 04 January 2007, pp. 607-622
- Print publication:
- December 2006
-
- Article
- Export citation