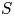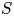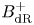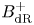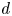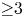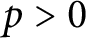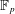Refine search
Actions for selected content:
21 results
On the weak Harder–Narasimhan stratification on
 $B_{\mathrm{dR}}^+$-affine Grassmannian
$B_{\mathrm{dR}}^+$-affine Grassmannian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 15 December 2025, pp. 2654-2711
- Print publication:
- October 2025
-
- Article
- Export citation
ON A COMPARISON BETWEEN DWORK AND RIGID COHOMOLOGIES OF PROJECTIVE COMPLEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 420-461
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weight filtrations on Selmer schemes and the effective Chabauty–Kim method
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1531-1605
- Print publication:
- July 2023
-
- Article
- Export citation
A Harder–Narasimhan stratification of the
 ${B^+_{{\rm dR}}}$-Grassmannian
${B^+_{{\rm dR}}}$-Grassmannian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 29 March 2023, pp. 711-745
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial dynamics and local analysis of small and grand orbits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 53-86
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOGARITHMIC DE RHAM–WITT COMPLEXES VIA THE DÉCALAGE OPERATOR
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 26 August 2021, pp. 1319-1382
- Print publication:
- May 2023
-
- Article
- Export citation
Rigid-analytic varieties with projective reduction violating Hodge symmetry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 625-640
- Print publication:
- March 2021
-
- Article
- Export citation
Faltings extension and Hodge-Tate filtration for abelian varieties over p-adic local fields with imperfect residue fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 247-263
- Print publication:
- June 2021
-
- Article
- Export citation
Degeneration of Kummer surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 April 2020, pp. 65-97
- Print publication:
- July 2021
-
- Article
- Export citation
LOGARITHMIC DE RHAM COMPARISON FOR OPEN RIGID SPACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 25 September 2019, e32
-
- Article
-
- You have access
- Open access
- Export citation
ON LOCAL FIELDS GENERATED BY DIVISION VALUES OF FORMAL DRINFELD MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 14 June 2019, pp. 459-472
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
On the Frequency of Algebraic Brauer Classes on Certain Log K3 Surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 551-563
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Optimal Quotients of Jacobians With ToricReduction and Component Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 6 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1362-1381
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
The Brauer–Manin pairing, class field theory, and motivic homology
-
- Journal:
- Nagoya Mathematical Journal / Volume 210 / June 2013
- Published online by Cambridge University Press:
- 11 January 2016, pp. 29-58
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
 $p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES
$p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 17 May 2013, e1
-
- Article
-
- You have access
- Open access
- Export citation
Formule du conducteur pour un caractère l-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 687-717
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
The canonical subgroup for families of abelian varieties
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 3 / May 2007
- Published online by Cambridge University Press:
- 04 December 2007, pp. 566-602
- Print publication:
- May 2007
-
- Article
-
- You have access
- Export citation
On $\ell$-independence for the étale cohomology of rigid spaces over local fields
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 2 / March 2007
- Published online by Cambridge University Press:
- 26 March 2007, pp. 393-422
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Stable reduction of finite covers of curves
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 13 January 2006, pp. 101-118
- Print publication:
- January 2006
-
- Article
-
- You have access
- Export citation
Le groupe de Chow d'une surface rationnelle sur un corps local
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 2 / March 2005
- Published online by Cambridge University Press:
- 10 February 2005, pp. 344-358
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation