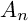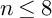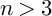Refine search
Actions for selected content:
90 results
Optimal bound for singularities on Fano type fibrations of relative dimension one
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 November 2025, e193
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pathological MMP singularities as αp-quotients
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 November 2025, e185
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the MMP for rank one foliations on threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 25 September 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On semi-ampleness of the moduli part
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EFFECTIVE BOUND FOR SINGULARITIES ON TORIC FIBRATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 779-795
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
Boundedness of slc degenerations of polarized log Calabi–Yau pairs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 September 2025, e144
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal Model Program for Normal Pairs along log Canonical Locus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 September 2025, e143
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic singularities and threefold flops in positive characteristic
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1188-1244
-
- Article
- Export citation
PROJECTIVELY FLAT FOLIATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 763-812
- Print publication:
- May 2025
-
- Article
- Export citation
Local Normal Forms of Noncommutative Functions
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complements and coregularity of Fano varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant geometry of singular cubic threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FANO FOURFOLDS WITH LARGE ANTICANONICAL BASE LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1021-1051
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NON-VANISHING RESULTS CONCERNING THE ANTI-CANONICAL BUNDLE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 201-218
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIGNESS OF THE TANGENT BUNDLE OF A FANO THREEFOLD WITH PICARD NUMBER TWO
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 104-133
- Print publication:
- March 2025
-
- Article
- Export citation
A REMARK ON FUJINO’S WORK ON THE CANONICAL BUNDLE FORMULA VIA PERIOD MAPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 79-92
- Print publication:
- March 2025
-
- Article
- Export citation
On the properness of the moduli space of stable surfaces over
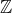 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the embedded Nash problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 16 October 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding geometrically integral del Pezzo surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 October 2024, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIRATIONAL GEOMETRY OF SEXTIC DOUBLE SOLIDS WITH A COMPOUND
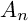 $A_n$ SINGULARITY
$A_n$ SINGULARITY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 970-1021
- Print publication:
- December 2024
-
- Article
- Export citation