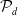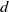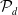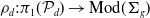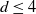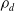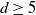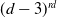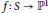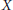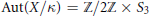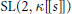Refine search
Actions for selected content:
19 results
EIGENPERIODS AND THE MODULI OF POINTS IN THE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 524-547
- Print publication:
- September 2025
-
- Article
- Export citation
On the monodromy group of the family of smooth quintic plane curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 November 2024, pp. 163-184
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homology supported in Lagrangian submanifolds in mirror quintic threefolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 709-724
- Print publication:
- September 2021
-
- Article
- Export citation
ORBIFOLD ASPECTS OF CERTAIN OCCULT PERIOD MAPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 137-156
- Print publication:
- September 2021
-
- Article
- Export citation
Arithmeticity of the monodromy of some Kodaira fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 114-157
- Print publication:
- January 2020
-
- Article
- Export citation
ALGEBRAIC ISOMONODROMIC DEFORMATIONS AND THE MAPPING CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 1497-1545
- Print publication:
- September 2021
-
- Article
- Export citation
THE KUGA–SATAKE CONSTRUCTION UNDER DEGENERATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 2165-2182
- Print publication:
- November 2020
-
- Article
- Export citation
INTEGRAL MONODROMY GROUPS OF KLOOSTERMAN SHEAVES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 08 June 2018, pp. 652-678
- Print publication:
- 2018
-
- Article
- Export citation
A Lower Bound on the Euler–Poincaré Characteristic of Certain Surfaces of General Type with a Linear Pencil of Hyperelliptic Curves
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 1 / 01 February 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 67-87
- Print publication:
- 01 February 2016
-
- Article
-
- You have access
- Export citation
The Fixed Point Locus of the Verschiebung on ℳX(2, 0) for Genus-2 Curves X in Charateristic 2
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 439-448
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
Moduli of products of stable varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 06 September 2013, pp. 2036-2070
- Print publication:
- December 2013
-
- Article
- Export citation
A Noether-Lefschetz theorem for varieties of r-planes in complete intersections
-
- Journal:
- Nagoya Mathematical Journal / Volume 206 / June 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 39-66
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On the Geometry of the Moduli Space of Real Binary Octics
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 4 / 01 August 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 755-797
- Print publication:
- 01 August 2011
-
- Article
-
- You have access
- Export citation
Generalizations of Clausen's Formula and algebraic transformations of Calabi–Yau differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 273-295
-
- Article
-
- You have access
- Export citation
Quantum cohomology of the Grassmannian and alternate Thom–Sebastiani
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 221-246
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
Variations of Mixed Hodge Structures of Multiple Polylogarithms
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 6 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1308-1338
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation
The Geometry of Quadratic Differential Systems with a Weak Focus of Third Order
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 2 / 01 April 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 310-343
- Print publication:
- 01 April 2004
-
- Article
-
- You have access
- Export citation
Numerical criteria for certain fiber spaces to be birationally trivial
-
- Journal:
- Nagoya Mathematical Journal / Volume 168 / 2002
- Published online by Cambridge University Press:
- 22 January 2016, pp. 93-103
- Print publication:
- 2002
-
- Article
-
- You have access
- Export citation
On Curves and Surfaces with Projectively Equivalent Hyperplane Sections
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 3 / 01 September 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 384-392
- Print publication:
- 01 September 1994
-
- Article
-
- You have access
- Export citation