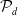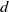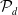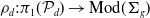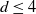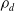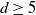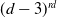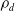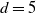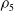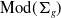1. Introduction
LetFootnote
1
![]() $\mathcal{P}_d$
denote the moduli space of smooth degree
$\mathcal{P}_d$
denote the moduli space of smooth degree
![]() $d$
plane curves. The tautological family of plane curves over
$d$
plane curves. The tautological family of plane curves over
![]() $\mathcal{P}_d$
determines a monodromy representation
$\mathcal{P}_d$
determines a monodromy representation
where
![]() $g =\binom{d-1}{2}$
and
$g =\binom{d-1}{2}$
and
![]() $\textrm{Mod}(\Sigma _g)$
is the mapping class group of the surface
$\textrm{Mod}(\Sigma _g)$
is the mapping class group of the surface
![]() $\Sigma _g$
of genus
$\Sigma _g$
of genus
![]() $g$
. This note concerns the problem of computing the image of
$g$
. This note concerns the problem of computing the image of
![]() $\rho _d$
.
$\rho _d$
.
The first step toward determining the image of
![]() $\rho _d$
was carried out by A. Beauville in [Reference Beauville4], building off of earlier work of W. Janssen [Reference Janssen18] and S. Chmutov [Reference Chmutov7]. Let
$\rho _d$
was carried out by A. Beauville in [Reference Beauville4], building off of earlier work of W. Janssen [Reference Janssen18] and S. Chmutov [Reference Chmutov7]. Let
![]() $\Psi : \textrm{Mod}(\Sigma _g) \to \mathrm{Sp}_{2g}({\mathbb{Z}})$
denote the symplectic representation of
$\Psi : \textrm{Mod}(\Sigma _g) \to \mathrm{Sp}_{2g}({\mathbb{Z}})$
denote the symplectic representation of
![]() $\textrm{Mod}(\Sigma _g)$
on
$\textrm{Mod}(\Sigma _g)$
on
![]() $H_1(\Sigma _g;{\mathbb{Z}})$
. Beauville determined
$H_1(\Sigma _g;{\mathbb{Z}})$
. Beauville determined
![]() $\Psi \circ \rho _d$
. He shows that for
$\Psi \circ \rho _d$
. He shows that for
![]() $d$
even it is a surjection, while for
$d$
even it is a surjection, while for
![]() $d$
odd it is the (finite-index) stabilizer of a certain spin structure. Naively, it is, therefore, possible that
$d$
odd it is the (finite-index) stabilizer of a certain spin structure. Naively, it is, therefore, possible that
![]() $\rho _d$
could surject onto
$\rho _d$
could surject onto
![]() $\textrm{Mod}(\Sigma _g)$
or onto a spin mapping class group, depending on the parity of
$\textrm{Mod}(\Sigma _g)$
or onto a spin mapping class group, depending on the parity of
![]() $d$
.
$d$
.
It is a folklore result that in general, this does not happen. There is an invariant called an
![]() $r$
-spin structure that provides an obstruction for
$r$
-spin structure that provides an obstruction for
![]() $f \in \textrm{Mod}(\Sigma _g)$
to be contained in
$f \in \textrm{Mod}(\Sigma _g)$
to be contained in
![]() $\mathrm{Im}(\rho _d)$
. This
$\mathrm{Im}(\rho _d)$
. This
![]() $r$
-spin structure is constructed in a natural way from a
$r$
-spin structure is constructed in a natural way from a
![]() $(d-3)^{rd}$
root of the canonical bundle of a plane curve; see Section 2.2 for further discussion. It follows from work of Sipe [Reference Sipe25] that for
$(d-3)^{rd}$
root of the canonical bundle of a plane curve; see Section 2.2 for further discussion. It follows from work of Sipe [Reference Sipe25] that for
![]() $d \ge 6$
, this obstruction is not detectable on the level of homology, that is, that Beauville’s upper bound is not sharp. We formulate this as a theorem, in the interest of giving a self-contained proof of a result which does not seem to be easily accessible in the literature.
$d \ge 6$
, this obstruction is not detectable on the level of homology, that is, that Beauville’s upper bound is not sharp. We formulate this as a theorem, in the interest of giving a self-contained proof of a result which does not seem to be easily accessible in the literature.
Theorem 1.1 (Folklore, Sipe [Reference Sipe25]). For all
![]() $d \ge 4$
, there is a finite-index subgroup
$d \ge 4$
, there is a finite-index subgroup
![]() $\textrm{Mod}(\Sigma _g)[\phi _d] \le \textrm{Mod}(\Sigma _g)$
for which
$\textrm{Mod}(\Sigma _g)[\phi _d] \le \textrm{Mod}(\Sigma _g)$
for which
For
![]() $d \ge 6$
, the containment
$d \ge 6$
, the containment
is strict. Consequently, for
![]() $d \ge 6$
, the same is true for
$d \ge 6$
, the same is true for
![]() $\mathrm{Im}(\rho _d)$
:
$\mathrm{Im}(\rho _d)$
:
In the statement of Theorem 1.1,
![]() $\phi _d \in H^1(T^{*,1}\Sigma _g;{\mathbb{Z}} / (d-3){\mathbb{Z}})$
, where
$\phi _d \in H^1(T^{*,1}\Sigma _g;{\mathbb{Z}} / (d-3){\mathbb{Z}})$
, where
![]() $T^{*,1}\Sigma _g$
denotes the unit cotangent bundle of
$T^{*,1}\Sigma _g$
denotes the unit cotangent bundle of
![]() $\Sigma _g$
, and
$\Sigma _g$
, and
![]() $\textrm{Mod}(\Sigma _g)[\phi _d]$
denotes the stabilizer of
$\textrm{Mod}(\Sigma _g)[\phi _d]$
denotes the stabilizer of
![]() $\phi _d$
in the natural action of
$\phi _d$
in the natural action of
![]() $\textrm{Mod}(\Sigma _g)$
on
$\textrm{Mod}(\Sigma _g)$
on
![]() $H^1(\Sigma _g;{\mathbb{Z}}/(d-3){\mathbb{Z}})$
. The class
$H^1(\Sigma _g;{\mathbb{Z}}/(d-3){\mathbb{Z}})$
. The class
![]() $\phi _d$
is an instance of an
$\phi _d$
is an instance of an
![]() $r$
-spin structure for
$r$
-spin structure for
![]() $r = d-3$
.
$r = d-3$
.
Our proof of Theorem 1.1 will be obtained by giving a construction of
![]() $\phi _d$
that makes the invariance of
$\phi _d$
that makes the invariance of
![]() $\phi _d$
under
$\phi _d$
under
![]() $\mathrm{Im}(\rho _d)$
transparent. Using a topological interpretation of
$\mathrm{Im}(\rho _d)$
transparent. Using a topological interpretation of
![]() $r$
-spin structures based on the work of S. Humphries and D. Johnson [Reference Humphries and Johnson17], it will then be possible to see how the invariance of
$r$
-spin structures based on the work of S. Humphries and D. Johnson [Reference Humphries and Johnson17], it will then be possible to see how the invariance of
![]() $\phi _d$
provides a strictly stronger constraint on
$\phi _d$
provides a strictly stronger constraint on
![]() $\mathrm{Im}(\rho _d)$
than that of Beauville.
$\mathrm{Im}(\rho _d)$
than that of Beauville.
The main original result of this paper concerns the problem of determining sufficient conditions for an element
![]() $f \in \textrm{Mod}(\Sigma _g)$
to be contained in
$f \in \textrm{Mod}(\Sigma _g)$
to be contained in
![]() $\mathrm{Im}(\rho _d)$
. For degrees
$\mathrm{Im}(\rho _d)$
. For degrees
![]() $d = 3, 4$
(where
$d = 3, 4$
(where
![]() $g = 1,3$
), it is known that
$g = 1,3$
), it is known that
![]() $\rho _d$
is a surjection. This is ultimately a consequence of the fact that generic curves of genus
$\rho _d$
is a surjection. This is ultimately a consequence of the fact that generic curves of genus
![]() $g = 1,3$
admit planar embeddings, unique up to an automorphism of
$g = 1,3$
admit planar embeddings, unique up to an automorphism of
![]() ${\mathbb{C}} P^2$
(the only exceptions being hyperelliptic curves in genus
${\mathbb{C}} P^2$
(the only exceptions being hyperelliptic curves in genus
![]() $3$
). The case
$3$
). The case
![]() $d = 3$
also follows immediately from Beauville’s computation, in light of the fact that
$d = 3$
also follows immediately from Beauville’s computation, in light of the fact that
![]() $\Psi$
is an isomorphism
$\Psi$
is an isomorphism
![]() $\Psi : \textrm{Mod}(\Sigma _1) \to SL_2({\mathbb{Z}})$
for
$\Psi : \textrm{Mod}(\Sigma _1) \to SL_2({\mathbb{Z}})$
for
![]() $g=1$
. This case is also closely related to the work of I. Dolgachev and A. Libgober [Reference Dolgachev and Libgober12]. The case
$g=1$
. This case is also closely related to the work of I. Dolgachev and A. Libgober [Reference Dolgachev and Libgober12]. The case
![]() $d = 4$
was treated by Y. Kuno [Reference Kuno20]. Theorem 1.2 thus treats the first case where planarity is an exceptional property for a curve to possess, and shows that despite this, the monodromy of the family of plane curves of degree
$d = 4$
was treated by Y. Kuno [Reference Kuno20]. Theorem 1.2 thus treats the first case where planarity is an exceptional property for a curve to possess, and shows that despite this, the monodromy of the family of plane curves of degree
![]() $5$
is still as large as possible.
$5$
is still as large as possible.
Theorem 1.2.
Let
![]() $d = 5$
. There is a (classical) spin structure of odd parity
$d = 5$
. There is a (classical) spin structure of odd parity
![]() $\phi _5 \in H^1(T^{*,1}\Sigma _6;{\mathbb{Z}}/2{\mathbb{Z}})$
with associated stabilizer
$\phi _5 \in H^1(T^{*,1}\Sigma _6;{\mathbb{Z}}/2{\mathbb{Z}})$
with associated stabilizer
![]() $\textrm{Mod}(\Sigma _6)[\phi _5] \le \textrm{Mod}(\Sigma _6)$
for which there is an equality
$\textrm{Mod}(\Sigma _6)[\phi _5] \le \textrm{Mod}(\Sigma _6)$
for which there is an equality
The methods of the paper are special to the case of
![]() $d = 5$
only in that a finite generating set for
$d = 5$
only in that a finite generating set for
![]() $\textrm{Mod}(\Sigma _g)[\phi _d] \cap \ker (\Psi )$
is known only for
$\textrm{Mod}(\Sigma _g)[\phi _d] \cap \ker (\Psi )$
is known only for
![]() $d \le 5$
; we are able to produce large collections of Dehn twists in
$d \le 5$
; we are able to produce large collections of Dehn twists in
![]() $\mathrm{Im}(\rho _d)$
for all
$\mathrm{Im}(\rho _d)$
for all
![]() $d$
. On the basis of this, we offer the following conjecture.
$d$
. On the basis of this, we offer the following conjecture.
Conjecture 1.2 (Monodromy of the universal plane curve). For all
![]() $d \ge 4$
, there is an equality
$d \ge 4$
, there is an equality
A version of Conjecture 1.2 was also formulated by R. Crétois and L. Lang [Reference Crétois and Lang8]. The paper [Reference Crétois and Lang8] is closely related to this one, treating the problem of monodromies of linear systems on toric surfaces.
Theorem 1.2 is obtained by a combination of techniques both from algebraic geometry and from the theory of the mapping class group. The starting point is Beauville’s work, which allows one to restrict attention to
![]() $\mathrm{Im}(\rho _5) \cap \mathcal{I}_6$
, where
$\mathrm{Im}(\rho _5) \cap \mathcal{I}_6$
, where
![]() $\mathcal{I}_6$
is the Torelli group (see Section 4.3 for the definition of the Torelli group).
$\mathcal{I}_6$
is the Torelli group (see Section 4.3 for the definition of the Torelli group).
The bridge between algebraic geometry and mapping class groups arises from the work of M. Lönne [Reference Lönne21]. The main theorem of [Reference Lönne21] gives an explicit presentation for the fundamental group of the space
![]() $\mathcal{P}_{n,d}$
of smooth hypersurfaces in
$\mathcal{P}_{n,d}$
of smooth hypersurfaces in
![]() ${\mathbb{C}} P^n$
of degree
${\mathbb{C}} P^n$
of degree
![]() $d$
. Picard–Lefschetz theory allows one to recognize Lönne’s generators as Dehn twists. Theorem 1.2 is then proved by carrying out a careful examination of the configuration of vanishing cycles as simple closed curves on a surface of genus
$d$
. Picard–Lefschetz theory allows one to recognize Lönne’s generators as Dehn twists. Theorem 1.2 is then proved by carrying out a careful examination of the configuration of vanishing cycles as simple closed curves on a surface of genus
![]() $6$
. This analysis is used to exhibit the elements of Johnson’s generating set for the Torelli group inside
$6$
. This analysis is used to exhibit the elements of Johnson’s generating set for the Torelli group inside
![]() $\mathrm{Im}(\rho _5)$
.
$\mathrm{Im}(\rho _5)$
.
In genus
![]() $6$
, Johnson’s generating set has
$6$
, Johnson’s generating set has
![]() $4470$
elements. In order to make this computation tractable, we find a new relation in
$4470$
elements. In order to make this computation tractable, we find a new relation in
![]() $\textrm{Mod}(\Sigma _g)$
known as the “genus-
$\textrm{Mod}(\Sigma _g)$
known as the “genus-
![]() $g$
star relation”. Using this, we reduce the problem to eight easily verified cases. An implicit corollary of the proof is a determination of a simple finite set of Dehn twist generators for the spin mapping class group
$g$
star relation”. Using this, we reduce the problem to eight easily verified cases. An implicit corollary of the proof is a determination of a simple finite set of Dehn twist generators for the spin mapping class group
![]() $\textrm{Mod}(\Sigma _6)[\phi _5]$
. An alternative set of generators was obtained by S. Hirose [ [Reference Hirose16], Theorem 6.1].
$\textrm{Mod}(\Sigma _6)[\phi _5]$
. An alternative set of generators was obtained by S. Hirose [ [Reference Hirose16], Theorem 6.1].
1.1. Update
As discussed in Footnote 1, this paper first appeared in 2016, and much has advanced in the intervening years. We provide here an up-to-date account of the state of affairs. Conjecture 1.3 has now been completely resolved, indeed in the broader setting of linear systems on smooth toric surfaces. The case when the
![]() $r$
-spin structure has
$r$
-spin structure has
![]() $r = 2$
was treated by Crétois–Lang in [Reference Crétois and Lang9]. The general case was resolved by the author in [Reference Salter24] (only up to finite index, in the case of
$r = 2$
was treated by Crétois–Lang in [Reference Crétois and Lang9]. The general case was resolved by the author in [Reference Salter24] (only up to finite index, in the case of
![]() $r$
even), and subsequently, the full conjecture was obtained by the author and Calderon in [Reference Calderon and Salter10]. As first observed by Calderon [Reference Calderon6],
$r$
even), and subsequently, the full conjecture was obtained by the author and Calderon in [Reference Calderon and Salter10]. As first observed by Calderon [Reference Calderon6],
![]() $r$
-spin mapping class groups (and the refinements to “framed mapping class groups”) appear in a diverse array of other monodromy problems, including strata of Abelian differentials [Reference Calderon6, Reference Calderon and Salter10, Reference Calderon and Salter11] and versal deformations of isolated plane curve singularities [Reference Portilla Cuadrado and Salter23].
$r$
-spin mapping class groups (and the refinements to “framed mapping class groups”) appear in a diverse array of other monodromy problems, including strata of Abelian differentials [Reference Calderon6, Reference Calderon and Salter10, Reference Calderon and Salter11] and versal deformations of isolated plane curve singularities [Reference Portilla Cuadrado and Salter23].
In [Reference Harris15], R. Harris investigates the kernel of the monodromy map, finding that for plane quartics, the kernel is isomorphic to the product of a free group of infinite rank with
![]() ${\mathbb{Z}}/3{\mathbb{Z}}$
. And in [Reference Banerjee3], Banerjee finds that the fundamental group of the ambient algebraic surface provides a further constraint on the monodromy of a linear system. This constraint is quite strong, forcing in some cases the monodromy to be of infinite index. It would be interesting to investigate Conjecture 1.3 for any linear system on a simply connected smooth algebraic surface.
${\mathbb{Z}}/3{\mathbb{Z}}$
. And in [Reference Banerjee3], Banerjee finds that the fundamental group of the ambient algebraic surface provides a further constraint on the monodromy of a linear system. This constraint is quite strong, forcing in some cases the monodromy to be of infinite index. It would be interesting to investigate Conjecture 1.3 for any linear system on a simply connected smooth algebraic surface.
1.2. Outline
Section 2 is devoted to the construction of
![]() $\phi _d$
. In Section 3, we recall some work of S. Humphries and D. Johnson that relates
$\phi _d$
. In Section 3, we recall some work of S. Humphries and D. Johnson that relates
![]() $H^1(T^{*,1} \Sigma _g; V)$
for an Abelian group
$H^1(T^{*,1} \Sigma _g; V)$
for an Abelian group
![]() $V$
to the notion of a “generalized winding number function”. We will use this perspective to prove that the invariance of
$V$
to the notion of a “generalized winding number function”. We will use this perspective to prove that the invariance of
![]() $\phi _d$
under
$\phi _d$
under
![]() $\mathrm{Im}(\rho _d)$
provides an obstruction to the surjectivity of
$\mathrm{Im}(\rho _d)$
provides an obstruction to the surjectivity of
![]() $\rho _d$
.
$\rho _d$
.
The proof of Theorem 1.2 is carried out in sections 4 through 7. Section 4 collects a number of results from the theory of mapping class groups. Section 5 recalls Lönne’s presentation and establishes some first properties of
![]() $\mathrm{Im}(\rho _d)$
. Section 6 continues the analysis of
$\mathrm{Im}(\rho _d)$
. Section 6 continues the analysis of
![]() $\mathrm{Im}(\rho _d)$
. Finally, Section 7 collects these results together to prove Theorem 1.2.
$\mathrm{Im}(\rho _d)$
. Finally, Section 7 collects these results together to prove Theorem 1.2.
2.
 $r^{th}$
roots of the canonical bundle and generalized spin structures
$r^{th}$
roots of the canonical bundle and generalized spin structures
2.1. Plane curves and
 $\mathcal{P}_d$
$\mathcal{P}_d$
A general reference for this paragraph is [ [Reference Dolgachev and Libgober12], Section 2].
By definition, a (projective) plane curve of degree
![]() $d$
is the vanishing locus
$d$
is the vanishing locus
![]() $V(f)$
in
$V(f)$
in
![]() ${\mathbb{C}} P^2$
of a nonzero homogeneous polynomial
${\mathbb{C}} P^2$
of a nonzero homogeneous polynomial
![]() $f(x,y,z)$
of degree
$f(x,y,z)$
of degree
![]() $d$
. The space of all plane curves is identified with
$d$
. The space of all plane curves is identified with
![]() ${\mathbb{C}} P^N$
, where
${\mathbb{C}} P^N$
, where
![]() $N =\binom{d+2}{2} - 1$
. A plane curve
$N =\binom{d+2}{2} - 1$
. A plane curve
![]() $X$
of degree
$X$
of degree
![]() $d$
is smooth if
$d$
is smooth if
![]() $X \cong \Sigma _g$
with
$X \cong \Sigma _g$
with
![]() $g =\binom{d-1}{2}$
, and otherwise
$g =\binom{d-1}{2}$
, and otherwise
![]() $X$
is said to be singular.
$X$
is said to be singular.
We define the discriminant as the set
The discriminant
![]() $\mathcal{D}_d$
is the vanishing locus of a polynomial
$\mathcal{D}_d$
is the vanishing locus of a polynomial
![]() $p_d$
known as the discriminant polynomial and is therefore a hypersurface in
$p_d$
known as the discriminant polynomial and is therefore a hypersurface in
![]() ${\mathbb{C}} P^N$
. The space of smooth plane curves is then defined as
${\mathbb{C}} P^N$
. The space of smooth plane curves is then defined as
The universal family of plane curves is the space
![]() $\mathfrak{X}_d \subset \mathcal{P}_d \times{\mathbb{C}} \mathbb{P}^2$
defined via
$\mathfrak{X}_d \subset \mathcal{P}_d \times{\mathbb{C}} \mathbb{P}^2$
defined via
The projection
![]() $\pi : \mathfrak{X}_d \to \mathcal{P}_d$
is the projection map for a
$\pi : \mathfrak{X}_d \to \mathcal{P}_d$
is the projection map for a
![]() $C^\infty$
fiber bundle structure on
$C^\infty$
fiber bundle structure on
![]() $\mathfrak{X}_d$
with fibers diffeomorphic to
$\mathfrak{X}_d$
with fibers diffeomorphic to
![]() $\Sigma _g$
.
$\Sigma _g$
.
2.2.
 $r$
-spin structures
$r$
-spin structures
Let
![]() $X$
be a smooth projective algebraic curve over
$X$
be a smooth projective algebraic curve over
![]() $\mathbb{C}$
and let
$\mathbb{C}$
and let
![]() $K \in \mathrm{Pic}(X)$
denote the canonical bundle.Footnote 2 Recall that a spin structure on
$K \in \mathrm{Pic}(X)$
denote the canonical bundle.Footnote 2 Recall that a spin structure on
![]() $X$
is an element
$X$
is an element
![]() $L \in \mathrm{Pic}(X)$
satisfying
$L \in \mathrm{Pic}(X)$
satisfying
![]() $L^{\otimes 2} = K$
. This admits an obvious generalization.
$L^{\otimes 2} = K$
. This admits an obvious generalization.
Definition 2.1.
An
![]() $r$
-spin structure is a line bundle
$r$
-spin structure is a line bundle
![]() $L \in \mathrm{Pic}(X)$
satisfying
$L \in \mathrm{Pic}(X)$
satisfying
![]() $L^{\otimes r} = K$
.
$L^{\otimes r} = K$
.
Let
![]() $T^{*,1}X$
denote the unit cotangent bundle of
$T^{*,1}X$
denote the unit cotangent bundle of
![]() $X$
, relative to an arbitrary Riemannian metric on
$X$
, relative to an arbitrary Riemannian metric on
![]() $X$
. Just as ordinary spin structures are closely related to
$X$
. Just as ordinary spin structures are closely related to
![]() $H^1(T^{*,1}X;{\mathbb{Z}}/2{\mathbb{Z}})$
, there is an analogous picture of
$H^1(T^{*,1}X;{\mathbb{Z}}/2{\mathbb{Z}})$
, there is an analogous picture of
![]() $r$
-spin structures.
$r$
-spin structures.
Proposition 2.2.
Let
![]() $L$
be an
$L$
be an
![]() $r$
-spin structure on
$r$
-spin structure on
![]() $X$
. Associated to
$X$
. Associated to
![]() $L$
are
$L$
are
-
1. a regular
 $r$
-sheeted covering space
$r$
-sheeted covering space
 $\widetilde{T^{*,1}X} \to T^{*,1}X$
with deck group
$\widetilde{T^{*,1}X} \to T^{*,1}X$
with deck group
 ${\mathbb{Z}}/n{\mathbb{Z}}$
, and
${\mathbb{Z}}/n{\mathbb{Z}}$
, and
-
2. a cohomology class
 $\phi _L \in H^1(T^{*,1}X;{\mathbb{Z}}/r{\mathbb{Z}})$
restricting to a generator of the cohomology
$\phi _L \in H^1(T^{*,1}X;{\mathbb{Z}}/r{\mathbb{Z}})$
restricting to a generator of the cohomology
 $H^1(S^1;{\mathbb{Z}}/r{\mathbb{Z}})$
of the fiber of
$H^1(S^1;{\mathbb{Z}}/r{\mathbb{Z}})$
of the fiber of
 $T^{*,1}X \to X$
.
$T^{*,1}X \to X$
.
Proof. In view of the equality
![]() $L^{\otimes r} = K$
in
$L^{\otimes r} = K$
in
![]() $\mathrm{Pic}(X)$
, taking
$\mathrm{Pic}(X)$
, taking
![]() $r^{th}$
powers in the fiber induces a map
$r^{th}$
powers in the fiber induces a map
![]() $\mu : L \to K$
. Let
$\mu : L \to K$
. Let
![]() $L^\circ$
denote the complement of the zero section in
$L^\circ$
denote the complement of the zero section in
![]() $L$
and define
$L$
and define
![]() $K^\circ$
similarly. Then
$K^\circ$
similarly. Then
![]() $\mu : L^\circ \to K^\circ$
is an
$\mu : L^\circ \to K^\circ$
is an
![]() $r$
-sheeted covering space with deck group
$r$
-sheeted covering space with deck group
![]() ${\mathbb{Z}}/r{\mathbb{Z}}$
induced from the multiplicative action of the
${\mathbb{Z}}/r{\mathbb{Z}}$
induced from the multiplicative action of the
![]() $r^{th}$
roots of unity. The covering space
$r^{th}$
roots of unity. The covering space
![]() $\widetilde{T^{*,1}X} \to T^{*,1}X$
is obtained from
$\widetilde{T^{*,1}X} \to T^{*,1}X$
is obtained from
![]() $L^\circ \to K^\circ$
by restriction.
$L^\circ \to K^\circ$
by restriction.
As
![]() $\widetilde{T^{*,1}X} \to T^{*,1}X$
is a regular cover with deck group
$\widetilde{T^{*,1}X} \to T^{*,1}X$
is a regular cover with deck group
![]() ${\mathbb{Z}}/r{\mathbb{Z}}$
, the Galois correspondence for covering spaces asserts that
${\mathbb{Z}}/r{\mathbb{Z}}$
, the Galois correspondence for covering spaces asserts that
![]() $\widetilde{T^{*,1}X}$
is associated to some homomorphism
$\widetilde{T^{*,1}X}$
is associated to some homomorphism
![]() $\phi _L: \pi _1(T^{*,1}X) \to{\mathbb{Z}}/r{\mathbb{Z}}$
. This gives rise to a class, also denoted
$\phi _L: \pi _1(T^{*,1}X) \to{\mathbb{Z}}/r{\mathbb{Z}}$
. This gives rise to a class, also denoted
![]() $\phi _L$
, in
$\phi _L$
, in
![]() $H^1(T^{1,*}X;{\mathbb{Z}}/r{\mathbb{Z}})$
. On a given fiber of
$H^1(T^{1,*}X;{\mathbb{Z}}/r{\mathbb{Z}})$
. On a given fiber of
![]() $T^{*,1}X \to X$
, the covering
$T^{*,1}X \to X$
, the covering
![]() $\widetilde{T^{*,1}X}\to T^{*,1}X$
restricts to an
$\widetilde{T^{*,1}X}\to T^{*,1}X$
restricts to an
![]() $r$
-sheeted cover
$r$
-sheeted cover
![]() $S^1 \to S^1$
; this proves the assertion concerning the restriction of
$S^1 \to S^1$
; this proves the assertion concerning the restriction of
![]() $\phi _L$
to
$\phi _L$
to
![]() $H^1(S^1;{\mathbb{Z}}/r{\mathbb{Z}})$
.
$H^1(S^1;{\mathbb{Z}}/r{\mathbb{Z}})$
.
Our interest in
![]() $r$
-spin structures arises from the fact that degree-
$r$
-spin structures arises from the fact that degree-
![]() $d$
plane curves are equipped with a canonical
$d$
plane curves are equipped with a canonical
![]() $(d-3)$
-spin structure.
$(d-3)$
-spin structure.
Fact 2.3.
Let
![]() $X$
be a smooth degree-
$X$
be a smooth degree-
![]() $d$
plane curve,
$d$
plane curve,
![]() $d \ge 3$
. The canonical bundle
$d \ge 3$
. The canonical bundle
![]() $K \in \mathrm{Pic}(X)$
is induced from the restriction of
$K \in \mathrm{Pic}(X)$
is induced from the restriction of
![]() $\mathcal{O}(d-3) \in \mathrm{Pic}({\mathbb{C}}\mathbb{P}^2)$
. Consequently,
$\mathcal{O}(d-3) \in \mathrm{Pic}({\mathbb{C}}\mathbb{P}^2)$
. Consequently,
![]() $\mathcal{O}(1)$
determines a
$\mathcal{O}(1)$
determines a
![]() $(d-3)$
-spin structure on
$(d-3)$
-spin structure on
![]() $X$
for
$X$
for
![]() $d \ge 4$
.
$d \ge 4$
.
Let
![]() $\varpi : \mathfrak{X}_d \to{\mathbb{C}} \mathbb{P}^2$
denote the projection onto the second factor. Then
$\varpi : \mathfrak{X}_d \to{\mathbb{C}} \mathbb{P}^2$
denote the projection onto the second factor. Then
![]() $\varpi ^*(\mathcal{O}(d-3)) \in \mathrm{Pic}(\mathfrak{X}_d)$
restricts to the canonical bundle on each fiber, and
$\varpi ^*(\mathcal{O}(d-3)) \in \mathrm{Pic}(\mathfrak{X}_d)$
restricts to the canonical bundle on each fiber, and
![]() $\varpi ^*(\mathcal{O}(1))$
determines a
$\varpi ^*(\mathcal{O}(1))$
determines a
![]() $(d-3)$
-spin structure. Let
$(d-3)$
-spin structure. Let
![]() $T^{*,1}\mathfrak{X}_d$
denote the
$T^{*,1}\mathfrak{X}_d$
denote the
![]() $S^1$
-bundle over
$S^1$
-bundle over
![]() $\mathfrak{X}_d$
for which the fiber over
$\mathfrak{X}_d$
for which the fiber over
![]() $(X,x)$
consists of the unit cotangent vectors
$(X,x)$
consists of the unit cotangent vectors
![]() $T^{*,1}_x X$
.
$T^{*,1}_x X$
.
Definition 2.4. The cohomology class
is obtained by applying the construction of Proposition 2.2 to the pair of line bundles
![]() $\varpi ^*(\mathcal{O}(1))$
,
$\varpi ^*(\mathcal{O}(1))$
,
![]() $\varpi ^*(\mathcal{O}(d-3)) \in \mathrm{Pic}(\mathfrak{X}_d)$
.
$\varpi ^*(\mathcal{O}(d-3)) \in \mathrm{Pic}(\mathfrak{X}_d)$
.
3. Generalized winding numbers and obstructions to surjectivity
In this section, we prove that the existence of
![]() $\phi _d$
gives rise to an obstruction for a mapping class
$\phi _d$
gives rise to an obstruction for a mapping class
![]() $f \in \textrm{Mod}(\Sigma _g)$
to be contained in
$f \in \textrm{Mod}(\Sigma _g)$
to be contained in
![]() $\mathrm{Im}(\rho _d)$
. For any system of coefficients
$\mathrm{Im}(\rho _d)$
. For any system of coefficients
![]() $V$
, there is a natural action of
$V$
, there is a natural action of
![]() $\textrm{Mod}(\Sigma _g)$
on
$\textrm{Mod}(\Sigma _g)$
on
![]() $H^1(T^{*,1}\Sigma _g; V)$
, which extends the action of
$H^1(T^{*,1}\Sigma _g; V)$
, which extends the action of
![]() $\textrm{Mod}(\Sigma _g)$
on
$\textrm{Mod}(\Sigma _g)$
on
![]() $H^1(\Sigma _g; V)$
via
$H^1(\Sigma _g; V)$
via
![]() $\Psi$
. To prove Theorem1.1, it therefore suffices to prove that the stabilizer
$\Psi$
. To prove Theorem1.1, it therefore suffices to prove that the stabilizer
![]() $\textrm{Mod}(\Sigma _g)[\phi _d]$
of each nonzero element of
$\textrm{Mod}(\Sigma _g)[\phi _d]$
of each nonzero element of
![]() $H^1(T^{*,1}\Sigma _g;{\mathbb{Z}}/(d-3){\mathbb{Z}})$
is not the full group
$H^1(T^{*,1}\Sigma _g;{\mathbb{Z}}/(d-3){\mathbb{Z}})$
is not the full group
![]() $\Psi ^{-1}(\Psi (\mathrm{Im}(\rho _d)))$
.
$\Psi ^{-1}(\Psi (\mathrm{Im}(\rho _d)))$
.
The natural setting for what follows is in the unit tangent bundle of a surface, which we write
![]() $T^1\Sigma$
. Of course, a choice of Riemannian metric on
$T^1\Sigma$
. Of course, a choice of Riemannian metric on
![]() $\Sigma$
identifies
$\Sigma$
identifies
![]() $T^1 \Sigma$
with
$T^1 \Sigma$
with
![]() $T^{*,1} \Sigma$
, and a choice of metric in each fiber identifies
$T^{*,1} \Sigma$
, and a choice of metric in each fiber identifies
![]() $T^{*,1} \mathfrak{X}_d$
with the “vertical unit tangent bundle”
$T^{*,1} \mathfrak{X}_d$
with the “vertical unit tangent bundle”
![]() $T^1 \mathfrak{X}_d$
; we will make no further comment on these matters.
$T^1 \mathfrak{X}_d$
; we will make no further comment on these matters.
The basis for our approach is the work of Humphries–Johnson [Reference Humphries and Johnson17], which gives an interpretation of
![]() $H^1(T^1 \Sigma _g; V)$
as the space of “
$H^1(T^1 \Sigma _g; V)$
as the space of “
![]() $V$
-valued generalized winding number functions”. A basic notion here is that of a Johnson lift. For our purposes, a simple closed curve is a
$V$
-valued generalized winding number functions”. A basic notion here is that of a Johnson lift. For our purposes, a simple closed curve is a
![]() $C^1$
-embedded
$C^1$
-embedded
![]() $S^1$
-submanifold.
$S^1$
-submanifold.
Definition 3.1.
Let
![]() $a$
be a simple closed curve on the surface
$a$
be a simple closed curve on the surface
![]() $\Sigma$
given by a unit-speed
$\Sigma$
given by a unit-speed
![]() $C^1$
embedding
$C^1$
embedding
![]() $a: S^1 \to \Sigma$
. A choice of orientation on
$a: S^1 \to \Sigma$
. A choice of orientation on
![]() $S^1$
induces an orientation on
$S^1$
induces an orientation on
![]() $a$
, as well as providing a coherent identification
$a$
, as well as providing a coherent identification
![]() $T^1_xS^1 = \{-1,1\}$
for each
$T^1_xS^1 = \{-1,1\}$
for each
![]() $x \in S^1$
. The Johnson lift of
$x \in S^1$
. The Johnson lift of
![]() $a$
, written
$a$
, written
![]() $\vec a$
, is the map
$\vec a$
, is the map
![]() $\vec a: S^1 \to T^1 \Sigma$
given by
$\vec a: S^1 \to T^1 \Sigma$
given by
That is, the Johnson lift of
![]() $a$
is simply the curve in
$a$
is simply the curve in
![]() $T^1\Sigma$
induced from
$T^1\Sigma$
induced from
![]() $a$
by tracking the tangent vector.
$a$
by tracking the tangent vector.
The Johnson lift allows for the evaluation of elements of
![]() $H^1(T^1\Sigma ;V)$
on simple closed curves. Let
$H^1(T^1\Sigma ;V)$
on simple closed curves. Let
![]() $\Sigma$
be a surface,
$\Sigma$
be a surface,
![]() $V$
an Abelian group, and
$V$
an Abelian group, and
![]() $\alpha \in H^1(T^1 \Sigma ; V)$
a cohomology class. Let
$\alpha \in H^1(T^1 \Sigma ; V)$
a cohomology class. Let
![]() $a$
be a simple closed curve. By an abuse of notation, we write
$a$
be a simple closed curve. By an abuse of notation, we write
![]() $\alpha (a)$
for the evaluation of
$\alpha (a)$
for the evaluation of
![]() $\alpha$
on the
$\alpha$
on the
![]() $1$
-cycle determined by the Johnson lift
$1$
-cycle determined by the Johnson lift
![]() $\vec a$
. In this context, we call
$\vec a$
. In this context, we call
![]() $\alpha$
a “generalized winding number function”.Footnote
3
In [Reference Humphries and Johnson17], it is shown that this pairing satisfies the following properties:
$\alpha$
a “generalized winding number function”.Footnote
3
In [Reference Humphries and Johnson17], it is shown that this pairing satisfies the following properties:
Theorem 3.2 (Humphries–Johnson).
-
(i) The evaluation
 $\alpha (a) \in V$
is well defined on the isotopy class of
$\alpha (a) \in V$
is well defined on the isotopy class of
 $a$
.
$a$
. -
(ii) (Twist-linearity) If
 $b$
is another simple closed curve and
$b$
is another simple closed curve and
 $T_b$
denotes the Dehn twist about
$T_b$
denotes the Dehn twist about
 $b$
, then
$b$
, then
 $\alpha$
is “twist-linear” in the following sense:
(1)where
$\alpha$
is “twist-linear” in the following sense:
(1)where \begin{equation} \alpha (T_b(a)) = \alpha (a) + \langle{a,b} \rangle \alpha (b), \end{equation}
\begin{equation} \alpha (T_b(a)) = \alpha (a) + \langle{a,b} \rangle \alpha (b), \end{equation}
 $\langle{a,b} \rangle$
denotes the algebraic intersection pairing.
$\langle{a,b} \rangle$
denotes the algebraic intersection pairing.
-
(iii) Let
 $\zeta$
be a curve enclosing a small null-homotopic disk on
$\zeta$
be a curve enclosing a small null-homotopic disk on
 $\Sigma$
, and let
$\Sigma$
, and let
 $S \subset \Sigma$
be a subsurface with boundary components
$S \subset \Sigma$
be a subsurface with boundary components
 $b_1, \dots, b_k$
. If each
$b_1, \dots, b_k$
. If each
 $b_i$
is oriented so that
$b_i$
is oriented so that
 $S$
is on the left and
$S$
is on the left and
 $\zeta$
is oriented similarly, then
(2)where
$\zeta$
is oriented similarly, then
(2)where \begin{equation} \alpha (b_1) + \dots +\alpha (b_k) = \chi (S) \alpha (\zeta ), \end{equation}
\begin{equation} \alpha (b_1) + \dots +\alpha (b_k) = \chi (S) \alpha (\zeta ), \end{equation}
 $\chi (S)$
is the Euler characteristic of
$\chi (S)$
is the Euler characteristic of
 $S$
.
$S$
.
Remark 3.3.
Humprhies–Johnson in fact establish much more: they prove that every
![]() $V$
-valued twist-linear function arises as a class
$V$
-valued twist-linear function arises as a class
![]() $\alpha \in H^1(T^1\Sigma ; V)$
. For what follows we only need the results of Theorem
3.2
.
$\alpha \in H^1(T^1\Sigma ; V)$
. For what follows we only need the results of Theorem
3.2
.
Proof of Theorem 1.1. Consider the class
![]() $\phi _d \in H^1(T^{*,1}\mathfrak{X}_d;{\mathbb{Z}}/(d-3){\mathbb{Z}})$
. The above discussion implies that on a given fiber
$\phi _d \in H^1(T^{*,1}\mathfrak{X}_d;{\mathbb{Z}}/(d-3){\mathbb{Z}})$
. The above discussion implies that on a given fiber
![]() $X$
of
$X$
of
![]() $\mathfrak{X}_d \to \mathcal{P}_d$
, the restriction of
$\mathfrak{X}_d \to \mathcal{P}_d$
, the restriction of
![]() $\phi _d$
determines a generalized winding number function; we write
$\phi _d$
determines a generalized winding number function; we write
![]() $\alpha _d \in H^1(T^1X;{\mathbb{Z}}/(d-3){\mathbb{Z}})$
for this class. Since
$\alpha _d \in H^1(T^1X;{\mathbb{Z}}/(d-3){\mathbb{Z}})$
for this class. Since
![]() $\alpha _d$
is induced from the globally defined form
$\alpha _d$
is induced from the globally defined form
![]() $\phi _d$
, it follows that
$\phi _d$
, it follows that
![]() $\alpha _d$
is monodromy-invariant: if
$\alpha _d$
is monodromy-invariant: if
![]() $f \in \mathrm{Im}(\rho _d)$
, then for any simple closed curve
$f \in \mathrm{Im}(\rho _d)$
, then for any simple closed curve
![]() $a$
on
$a$
on
![]() $X$
, the equation
$X$
, the equation
must hold. Consequently,
as claimed.
We wish to exhibit a nonseparating simple closed curve
![]() $b$
for which
$b$
for which
![]() $\alpha _d(b) \ne 0$
. Given such a
$\alpha _d(b) \ne 0$
. Given such a
![]() $b$
, there is another simple closed curve
$b$
, there is another simple closed curve
![]() $a$
satisfying
$a$
satisfying
![]() $\langle{a,b} \rangle = 1$
. Then the twist-linearity condition (1) will show that
$\langle{a,b} \rangle = 1$
. Then the twist-linearity condition (1) will show that
this contradicts (3). It follows that the Dehn twist
![]() $T_b$
for such a curve cannot be contained in
$T_b$
for such a curve cannot be contained in
![]() $\textrm{Mod}(\Sigma _g)[\phi _d]$
.
$\textrm{Mod}(\Sigma _g)[\phi _d]$
.
In the case when
![]() $d$
is even, when
$d$
is even, when
![]() $\Psi ^{-1}(\Psi (\mathrm{Im}(\rho _d))) = \textrm{Mod}(\Sigma _g)$
, this will prove Theorem1.1. For
$\Psi ^{-1}(\Psi (\mathrm{Im}(\rho _d))) = \textrm{Mod}(\Sigma _g)$
, this will prove Theorem1.1. For
![]() $d$
odd, there is an additional complication. Here, the class
$d$
odd, there is an additional complication. Here, the class
![]() $\frac{d-3}{2} \phi _d \in H^1(T^{*,1}\mathfrak{X}_d;{\mathbb{Z}}/2{\mathbb{Z}})$
determines an ordinary spin structure, and according to Beauville, the group
$\frac{d-3}{2} \phi _d \in H^1(T^{*,1}\mathfrak{X}_d;{\mathbb{Z}}/2{\mathbb{Z}})$
determines an ordinary spin structure, and according to Beauville, the group
![]() $\Psi (\textrm{Mod}(\Sigma _g)[\phi _d])$
is the stabilizer of
$\Psi (\textrm{Mod}(\Sigma _g)[\phi _d])$
is the stabilizer of
![]() $\frac{d-3}{2}\phi _d$
in
$\frac{d-3}{2}\phi _d$
in
![]() $\mathrm{Sp}(2g,{\mathbb{Z}})$
. We must, therefore, exhibit a curve
$\mathrm{Sp}(2g,{\mathbb{Z}})$
. We must, therefore, exhibit a curve
![]() $b$
for which
$b$
for which
![]() $\alpha _d(b)$
is nonzero and
$\alpha _d(b)$
is nonzero and
![]() $\frac{d-3}{2}$
-torsion. Equation (1) shows that such a curve does stabilize the spin structure
$\frac{d-3}{2}$
-torsion. Equation (1) shows that such a curve does stabilize the spin structure
![]() $\frac{d-3}{2} \phi _d$
, but not the refinement to a
$\frac{d-3}{2} \phi _d$
, but not the refinement to a
![]() $(d-3)$
-spin structure
$(d-3)$
-spin structure
![]() $\phi _d$
.
$\phi _d$
.
It remains to exhibit a suitable curve
![]() $b$
. It follows easily from the twist-linearity condition (1) that given any subsurface
$b$
. It follows easily from the twist-linearity condition (1) that given any subsurface
![]() $S \subset X$
of genus
$S \subset X$
of genus
![]() $1$
with one boundary component, there is some (necessarily nonseparating) curve
$1$
with one boundary component, there is some (necessarily nonseparating) curve
![]() $c$
contained in
$c$
contained in
![]() $S$
with
$S$
with
![]() $\alpha _d(c) = 0$
. Let
$\alpha _d(c) = 0$
. Let
![]() $S_1,S_2,S_3$
be a collection of mutually disjoint subsurfaces of genus
$S_1,S_2,S_3$
be a collection of mutually disjoint subsurfaces of genus
![]() $1$
with one boundary component, and let
$1$
with one boundary component, and let
![]() $c_1, c_2, c_3$
be curves satisfying
$c_1, c_2, c_3$
be curves satisfying
![]() $\alpha _d(c_i) = 0$
, and for which
$\alpha _d(c_i) = 0$
, and for which
![]() $c_i$
is contained in
$c_i$
is contained in
![]() $S_i$
(recall that
$S_i$
(recall that
![]() $d \ge 6$
and so the genus of
$d \ge 6$
and so the genus of
![]() $X$
is
$X$
is
![]() $g \ge 10$
). Choose
$g \ge 10$
). Choose
![]() $b$
disjoint from all
$b$
disjoint from all
![]() $c_i$
so that the collection of curves
$c_i$
so that the collection of curves
![]() $b, c_1,c_2, c_3$
encloses a subsurface
$b, c_1,c_2, c_3$
encloses a subsurface
![]() $\Sigma$
homeomorphic to a sphere with
$\Sigma$
homeomorphic to a sphere with
![]() $4$
boundary components. From (2) and the construction of the
$4$
boundary components. From (2) and the construction of the
![]() $c_i$
, it follows that when
$c_i$
, it follows that when
![]() $b$
is suitably oriented, it satisfies
$b$
is suitably oriented, it satisfies
Recall that by Proposition 2.2.2, the element
![]() $\alpha _d(\zeta ) \in{\mathbb{Z}}/(d-3){\mathbb{Z}}$
is primitive. Thus,
$\alpha _d(\zeta ) \in{\mathbb{Z}}/(d-3){\mathbb{Z}}$
is primitive. Thus,
![]() $\alpha _d(b) \ne 0$
for any
$\alpha _d(b) \ne 0$
for any
![]() $d$
, but is
$d$
, but is
![]() $\frac{d-3}{2}$
-torsion when
$\frac{d-3}{2}$
-torsion when
![]() $d$
is odd, as required.
$d$
is odd, as required.
4. Results from the theory of the mapping class group
We turn now to the proof of Theorem 1.2. From this section onward, we adopt the conventions and notations of the reference [Reference Farb and Margalit13]. In particular, the left-handed Dehn twist about a curve
![]() $c$
is written
$c$
is written
![]() $T_c$
, and the geometric intersection number between curves
$T_c$
, and the geometric intersection number between curves
![]() $a,b$
is written
$a,b$
is written
![]() $i(a,b)$
. We pause briefly to establish some further conventions. We will often refer to a simple closed curve as simply a “curve” and will often confuse the distinction between a curve and its isotopy class. Unless otherwise specified, we will assume that all intersections between curves are essential.
$i(a,b)$
. We pause briefly to establish some further conventions. We will often refer to a simple closed curve as simply a “curve” and will often confuse the distinction between a curve and its isotopy class. Unless otherwise specified, we will assume that all intersections between curves are essential.
4.1. The change-of-coordinates principle
The change-of-coordinates principle roughly asserts that if two configurations of simple closed curves and arcs on a surface have the same intersection pattern, then there is a homeomorphism taking one configuration to the other. There are many variants of the change-of-coordinates principle, all based on the classification of surfaces. See the discussion in [ [Reference Farb and Margalit13], Section 1.3.2].
4.1.1. Basic principle
Suppose
![]() $c_1, \dots, c_n$
and
$c_1, \dots, c_n$
and
![]() $d_1, \dots, d_n$
are configurations of curves on a surface
$d_1, \dots, d_n$
are configurations of curves on a surface
![]() $S$
all meeting transversely. The surface
$S$
all meeting transversely. The surface
![]() $\overline{S \setminus \{c_i\}}$
has a labeling on segments of its boundary, corresponding to the segments of the curves
$\overline{S \setminus \{c_i\}}$
has a labeling on segments of its boundary, corresponding to the segments of the curves
![]() $c_i$
from which the boundary component arises. Suppose there is a homeomorphism
$c_i$
from which the boundary component arises. Suppose there is a homeomorphism
taking every boundary segment labeled by
![]() $c_i$
to the corresponding
$c_i$
to the corresponding
![]() $d_i$
segment. Then
$d_i$
segment. Then
![]() $f$
can be extended to a homeomorphsim
$f$
can be extended to a homeomorphsim
![]() $f: S \to S$
taking the configuration
$f: S \to S$
taking the configuration
![]() $c_i$
to
$c_i$
to
![]() $d_i$
.
$d_i$
.
We illustrate this in the case of chains.
Definition 4.1.
Let
![]() $S$
be a surface. A chain on
$S$
be a surface. A chain on
![]() $S$
of length
$S$
of length
![]() $k$
is a collection of curves
$k$
is a collection of curves
![]() $(c_1, \dots, c_k)$
for which the geometric intersection number
$(c_1, \dots, c_k)$
for which the geometric intersection number
![]() $i(c_i, c_j)$
is
$i(c_i, c_j)$
is
![]() $1$
if
$1$
if
![]() ${\left |{i-j} \right |} = 1$
and
${\left |{i-j} \right |} = 1$
and
![]() $0$
otherwise. If
$0$
otherwise. If
![]() $C = (c_1, \dots, c_k)$
is a chain, the boundary of
$C = (c_1, \dots, c_k)$
is a chain, the boundary of
![]() $C$
, written
$C$
, written
![]() $\partial C$
, is defined to be the boundary of a small regular neighborhood of
$\partial C$
, is defined to be the boundary of a small regular neighborhood of
![]() $c_1 \cup \dots \cup c_k$
. When
$c_1 \cup \dots \cup c_k$
. When
![]() $k$
is even,
$k$
is even,
![]() $\partial C$
is a single (necessarily separating) curve, and when
$\partial C$
is a single (necessarily separating) curve, and when
![]() $k$
is odd,
$k$
is odd,
![]() $\partial C = d_1 \cup d_2$
consists of two curves
$\partial C = d_1 \cup d_2$
consists of two curves
![]() $d_1, d_2$
whose union separates
$d_1, d_2$
whose union separates
![]() $S$
.
$S$
.
Lemma 4.2 (Change-of-coordinates for chains). Let
![]() $(c_1, \dots, c_{k})$
and
$(c_1, \dots, c_{k})$
and
![]() $(d_1, \dots, d_{k})$
be chains of even length
$(d_1, \dots, d_{k})$
be chains of even length
![]() $k$
on a surface
$k$
on a surface
![]() $S$
. Then there is a homeomorphism
$S$
. Then there is a homeomorphism
![]() $f: S \to S$
for which
$f: S \to S$
for which
![]() $f(c_i) = d_i, 1\le i \le k$
.
$f(c_i) = d_i, 1\le i \le k$
.
Proof. See [ [Reference Farb and Margalit13], Section 1.3.2].
4.2. Some relations in the mapping class group
Proposition 4.3 (Braid relation). Let
![]() $S$
be a surface and
$S$
be a surface and
![]() $a,b$
curves on
$a,b$
curves on
![]() $S$
satisfying
$S$
satisfying
![]() $i(a,b) = 1$
. Then
$i(a,b) = 1$
. Then
On the level of curves,
Any such
![]() $a,b$
are necessarily non-separating.
$a,b$
are necessarily non-separating.
Conversely, if
![]() $a,b$
are curves on
$a,b$
are curves on
![]() $S$
in distinct isotopy classes that satisfy the braid relation (
4
), then
$S$
in distinct isotopy classes that satisfy the braid relation (
4
), then
![]() $i(a,b) = 1$
.
$i(a,b) = 1$
.
Proof. See [ [Reference Farb and Margalit13], Proposition 3.11] for the proof of the first assertion and [ [Reference Farb and Margalit13], Proposition 3.13] for the second.
4.2.1. The chain relation
The chain relation relates Dehn twists about curves in a chain to Dehn twists around the boundary. We will require a slightly less well known form of the chain relation for chains of odd length; see [ [Reference Farb and Margalit13], Section 4.4.1] for details.
Proposition 4.4 (Chain relation). Let
![]() $C = (c_1, \dots, c_k)$
be a chain with
$C = (c_1, \dots, c_k)$
be a chain with
![]() $k$
odd. Let
$k$
odd. Let
![]() $d_1, d_2$
denote the components of
$d_1, d_2$
denote the components of
![]() $\partial C$
. Then the following relation holds:
$\partial C$
. Then the following relation holds:
4.2.2. The genus-
 $g$
star relation
$g$
star relation
We will also need to make use of a novelFootnote 4 relation generalizing the star relation (setting
![]() $g=1$
below recovers the classical star relation).
$g=1$
below recovers the classical star relation).
Proposition 4.5 (Genus-
![]() $g$
star relation). With reference to the curves
$g$
star relation). With reference to the curves
![]() $a_1, a_2, c_1, \dots, c_{2g}, d_1, d_2, d_3$
on the surface
$a_1, a_2, c_1, \dots, c_{2g}, d_1, d_2, d_3$
on the surface
![]() $\Sigma _{g,3}$
of Figure
1
, the following relation holds in
$\Sigma _{g,3}$
of Figure
1
, the following relation holds in
![]() $\textrm{Mod}(\Sigma _{g,3})$
:
$\textrm{Mod}(\Sigma _{g,3})$
:

Figure 1. The genus-
![]() $g$
star relation.
$g$
star relation.
Proof. We will derive the genus-
![]() $g$
star relation from a more transparent relation in a braid group, making use of the theory of the liftable mapping class group as developed by Birman–Hilden [Reference Birman and Hilden5]. Figure 1 depicts a
$g$
star relation from a more transparent relation in a braid group, making use of the theory of the liftable mapping class group as developed by Birman–Hilden [Reference Birman and Hilden5]. Figure 1 depicts a
![]() $2:1$
covering
$2:1$
covering
![]() $\Sigma _{g,3} \to \Sigma _{0,2}$
ramified at
$\Sigma _{g,3} \to \Sigma _{0,2}$
ramified at
![]() $2g+1$
points. Number the ramification points clockwise
$2g+1$
points. Number the ramification points clockwise
![]() $p_1, \dots, p_{2g+1}$
and consider the mapping class group
$p_1, \dots, p_{2g+1}$
and consider the mapping class group
![]() $\operatorname{Mod}(\Sigma _{0,2,2g+1})$
relative to these points. The theory of Birman–Hilden implies that there is a finite-index subgroup of
$\operatorname{Mod}(\Sigma _{0,2,2g+1})$
relative to these points. The theory of Birman–Hilden implies that there is a finite-index subgroup of
![]() $\operatorname{Mod}(\Sigma _{0,2,2g+1})$
(the “liftable subgroup”) whose elements lift to mapping classes in
$\operatorname{Mod}(\Sigma _{0,2,2g+1})$
(the “liftable subgroup”) whose elements lift to mapping classes in
![]() $\operatorname{Mod}(\Sigma _{g,3})$
. Such lifts are unique up to the action of the deck group, and so there is a homomorphsim from the liftable subgroup into
$\operatorname{Mod}(\Sigma _{g,3})$
. Such lifts are unique up to the action of the deck group, and so there is a homomorphsim from the liftable subgroup into
![]() $\operatorname{Mod}(\Sigma _{g,3})$
. Consequently, any relation in the liftable subgroup induces a relation upstairs in
$\operatorname{Mod}(\Sigma _{g,3})$
. Consequently, any relation in the liftable subgroup induces a relation upstairs in
![]() $\operatorname{Mod}(\Sigma _{g,3})$
; this is the underlying principle of our argument.
$\operatorname{Mod}(\Sigma _{g,3})$
; this is the underlying principle of our argument.
Under the covering, the double-twist
![]() $T_{\delta _1}^2$
lifts to
$T_{\delta _1}^2$
lifts to
![]() $T_{d_1} \in \textrm{Mod}(\Sigma _{g,3})$
, and the twist
$T_{d_1} \in \textrm{Mod}(\Sigma _{g,3})$
, and the twist
![]() $T_{\delta _2}$
lifts to
$T_{\delta _2}$
lifts to
![]() $T_{d_2} T_{d_3}$
. The twist
$T_{d_2} T_{d_3}$
. The twist
![]() $T_\alpha$
lifts to
$T_\alpha$
lifts to
![]() $T_{a_1} T_{a_2}$
, and the half-twist
$T_{a_1} T_{a_2}$
, and the half-twist
![]() $\sigma _i$
lifts to
$\sigma _i$
lifts to
![]() $T_{c_i}$
. Let
$T_{c_i}$
. Let
![]() $f \in \operatorname{Mod}(\Sigma _{0,2,2g+1})$
be the push map moving each
$f \in \operatorname{Mod}(\Sigma _{0,2,2g+1})$
be the push map moving each
![]() $p_i$
clockwise to
$p_i$
clockwise to
![]() $p_{i+1}$
, with subscripts interpreted mod
$p_{i+1}$
, with subscripts interpreted mod
![]() $2g+1$
. One verifies the equality
$2g+1$
. One verifies the equality
It follows that
since
![]() $T_{\delta _1}$
is central. As
$T_{\delta _1}$
is central. As
![]() $f^{2g+1}$
is the push map around the core of the annulus, there is an equality
$f^{2g+1}$
is the push map around the core of the annulus, there is an equality
Combining these results,
Under the lifting described above, the relation (6) in
![]() $\operatorname{Mod}(\Sigma _{0,2,2g+1})$
lifts to the relation (5) in
$\operatorname{Mod}(\Sigma _{0,2,2g+1})$
lifts to the relation (5) in
![]() $\textrm{Mod}(\Sigma _{g,3})$
.
$\textrm{Mod}(\Sigma _{g,3})$
.
4.3. The Johnson generating set for
 $\mathcal{I}_g$
$\mathcal{I}_g$
There is a natural map
taking a mapping class
![]() $f$
to the induced automorphism
$f$
to the induced automorphism
![]() $f_*$
of
$f_*$
of
![]() $H_1(\Sigma _g;{\mathbb{Z}})$
. The Torelli group
$H_1(\Sigma _g;{\mathbb{Z}})$
. The Torelli group
![]() $\mathcal{I}_g$
is defined to be the kernel of this map:
$\mathcal{I}_g$
is defined to be the kernel of this map:
In [Reference Johnson19], Johnson produced a finite set of generators for
![]() $\mathcal{I}_g$
, for all
$\mathcal{I}_g$
, for all
![]() $g \ge 3$
. Elements of this generating set are known as chain maps. Let
$g \ge 3$
. Elements of this generating set are known as chain maps. Let
![]() $C = (c_1, \dots, c_k)$
be a chain of odd length with boundary
$C = (c_1, \dots, c_k)$
be a chain of odd length with boundary
![]() $\partial C = d_1 \cup d_2$
. There are exactly two ways to orient the collection of curves
$\partial C = d_1 \cup d_2$
. There are exactly two ways to orient the collection of curves
![]() $c_1, \dots, c_k$
in such a way that the algebraic intersection number
$c_1, \dots, c_k$
in such a way that the algebraic intersection number
![]() $c_i \cdot c_{i+1} = +1$
. Relative to such a choice, the chain map associated to
$c_i \cdot c_{i+1} = +1$
. Relative to such a choice, the chain map associated to
![]() $C$
is then the mapping class
$C$
is then the mapping class
![]() $T_{d_1} T_{d_2}^{-1}$
, where
$T_{d_1} T_{d_2}^{-1}$
, where
![]() $d_1$
is distinguished as the boundary component to the left of the curves
$d_1$
is distinguished as the boundary component to the left of the curves
![]() $c_1, c_3, \dots, c_k$
. The mapping class
$c_1, c_3, \dots, c_k$
. The mapping class
![]() $T_{d_1} T_{d-2}^{-1}$
is also called the bounding pair map for
$T_{d_1} T_{d-2}^{-1}$
is also called the bounding pair map for
![]() $d_1, d_2$
.
$d_1, d_2$
.
While a complete description of Johnson’s generating set is quite tidy and elegant, it has the disadvantage of requiring several preliminary notions before it can be stated. We, therefore, content ourselves with a distillation of his work that is more immediately applicable to our situation.

Figure 2. Curves involved in the Johnson generating set.
Theorem 4.6 (Johnson). For
![]() $g \ge 3$
, let
$g \ge 3$
, let
![]() $\Gamma \le \textrm{Mod}(\Sigma _g)$
be a subgroup that contains the Dehn twists about the curves
$\Gamma \le \textrm{Mod}(\Sigma _g)$
be a subgroup that contains the Dehn twists about the curves
![]() $c_1, \dots, c_{2g}$
shown in Figure
2
. Suppose that
$c_1, \dots, c_{2g}$
shown in Figure
2
. Suppose that
![]() $\Gamma$
contains all chain maps for the odd-length chains of the form
$\Gamma$
contains all chain maps for the odd-length chains of the form
![]() $(c_1, \dots, c_k)$
and
$(c_1, \dots, c_k)$
and
![]() $(\beta, c_5, \dots, c_k)$
. Then
$(\beta, c_5, \dots, c_k)$
. Then
![]() $\mathcal{I}_g \le \Gamma$
.
$\mathcal{I}_g \le \Gamma$
.
Proof. The interested reader should have no trouble deducing Theorem4.6 from the Main Theorem and Lemma 1(f) of [Reference Johnson19].
5. The Lönne presentation
In this section, we recall Lönne’s work [Reference Lönne21] computing
![]() $\pi _1(\mathcal{P}_d)$
and apply this to derive some first properties of the monodromy map
$\pi _1(\mathcal{P}_d)$
and apply this to derive some first properties of the monodromy map
![]() $\rho _d: \pi _1(\mathcal{P}_d) \to \textrm{Mod}(\Sigma _g)$
.
$\rho _d: \pi _1(\mathcal{P}_d) \to \textrm{Mod}(\Sigma _g)$
.
5.1. Picard–Lefschetz theory
Picard–Lefschetz theory concerns the problem of computing monodromies attached to singular points of holomorphic functions
![]() $f:{\mathbb{C}}^n \to{\mathbb{C}}$
. This then serves as the local theory underpinning more global monodromy computations. Our reference is [Reference Arnold, Gusein-Zade and Varchenko1].
$f:{\mathbb{C}}^n \to{\mathbb{C}}$
. This then serves as the local theory underpinning more global monodromy computations. Our reference is [Reference Arnold, Gusein-Zade and Varchenko1].
Let
![]() $U \subset{\mathbb{C}}^2$
and
$U \subset{\mathbb{C}}^2$
and
![]() $V \subset{\mathbb{C}}$
be open sets for which
$V \subset{\mathbb{C}}$
be open sets for which
![]() $0 \in V$
. Let
$0 \in V$
. Let
![]() $f(u,v): U \to V$
be a holomorphic function. Suppose
$f(u,v): U \to V$
be a holomorphic function. Suppose
![]() $f$
has an isolated critical value at
$f$
has an isolated critical value at
![]() $z = 0$
, and that there is a single corresponding critical point
$z = 0$
, and that there is a single corresponding critical point
![]() $p \in{\mathbb{C}}^2$
. Suppose that
$p \in{\mathbb{C}}^2$
. Suppose that
![]() $p$
is of Morse type in the sense that the Hessian
$p$
is of Morse type in the sense that the Hessian
 \begin{equation*} \left (\begin {array}{c@{\quad}c} {\dfrac {\partial ^2 f}{\partial ^2 x}} & {\dfrac {\partial ^2 f}{\partial x \partial y}} \\[15pt] \dfrac {\partial ^2 f}{\partial y \partial x} & {\dfrac {\partial ^2 f}{\partial ^2 y}} \end {array}\right ) \end{equation*}
\begin{equation*} \left (\begin {array}{c@{\quad}c} {\dfrac {\partial ^2 f}{\partial ^2 x}} & {\dfrac {\partial ^2 f}{\partial x \partial y}} \\[15pt] \dfrac {\partial ^2 f}{\partial y \partial x} & {\dfrac {\partial ^2 f}{\partial ^2 y}} \end {array}\right ) \end{equation*}
is non-singular at
![]() $p$
. Equivalently,
$p$
. Equivalently,
![]() $f$
is analytically equivalent to
$f$
is analytically equivalent to
![]() $f(u,v) = uv$
, the union of two lines crossing transversely.
$f(u,v) = uv$
, the union of two lines crossing transversely.
In such a situation, the fiber
![]() $f^{-1}(z)$
for
$f^{-1}(z)$
for
![]() $z \ne 0$
is diffeomorphic to an open annulus. The core curve of such an annulus is called a vanishing cycle. Let
$z \ne 0$
is diffeomorphic to an open annulus. The core curve of such an annulus is called a vanishing cycle. Let
![]() $\gamma$
be a small circle in
$\gamma$
be a small circle in
![]() $\mathbb{C}$
enclosing only the critical value at
$\mathbb{C}$
enclosing only the critical value at
![]() $z = 0$
. Let
$z = 0$
. Let
![]() $z_1 \in \gamma$
be a basepoint with corresponding core curve
$z_1 \in \gamma$
be a basepoint with corresponding core curve
![]() $c\subset f^{-1}(z_1)$
. The Picard–Lefschetz theorem describes the monodromy obtained by traversing
$c\subset f^{-1}(z_1)$
. The Picard–Lefschetz theorem describes the monodromy obtained by traversing
![]() $\gamma$
.
$\gamma$
.
More generally, an algebraic curve
![]() $C$
is said to have a nodal singularity at
$C$
is said to have a nodal singularity at
![]() $p \in C$
if there is an analytic local equation for
$p \in C$
if there is an analytic local equation for
![]() $C$
near
$C$
near
![]() $p$
of the form
$p$
of the form
![]() $f(u,v) = uv$
. Perturbing
$f(u,v) = uv$
. Perturbing
![]() $C$
slightly to a smooth
$C$
slightly to a smooth
![]() $C'$
, the intersection of
$C'$
, the intersection of
![]() $C'$
with a small ball near
$C'$
with a small ball near
![]() $p$
is again an annulus, and the core curve is again called a vanishing cycle.
$p$
is again an annulus, and the core curve is again called a vanishing cycle.
Theorem 5.1 (Picard–Lefschetz for
![]() $n = 2$
). With reference to the preceding discussion, the monodromy
$n = 2$
). With reference to the preceding discussion, the monodromy
![]() $\mu \in \textrm{Mod}(f^{-1}(z_1))$
attached to traversing
$\mu \in \textrm{Mod}(f^{-1}(z_1))$
attached to traversing
![]() $\gamma$
counter-clockwise is given by a right-handed Dehn twist about the vanishing cycle:
$\gamma$
counter-clockwise is given by a right-handed Dehn twist about the vanishing cycle:
More generally, let
![]() $D^*$
denote the punctured unit disk
$D^*$
denote the punctured unit disk
and write
![]() $D = \{w \in{\mathbb{C}} \mid \left | w \right | \le 1\}$
for the closed unit disk.
$D = \{w \in{\mathbb{C}} \mid \left | w \right | \le 1\}$
for the closed unit disk.
Let
![]() $f(x,y,z)$
be a homogeneous polynomial of degree
$f(x,y,z)$
be a homogeneous polynomial of degree
![]() $d$
with the following properties:
$d$
with the following properties:
-
1. For
 $c \in D$
, the plane curve
$c \in D$
, the plane curve
 $c z^d - f(x,y,z)$
is singular only for
$c z^d - f(x,y,z)$
is singular only for
 $c = 0$
.
$c = 0$
. -
2. The only critical point for
 $f$
of the form
$f$
of the form
 $(x,y,0)$
is the point
$(x,y,0)$
is the point
 $(0,0,0)$
.
$(0,0,0)$
. -
3. The function
 $f(x,y,1)$
has a single critical point of Morse type at
$f(x,y,1)$
has a single critical point of Morse type at
 $(x,y) = (0,0)$
.
$(x,y) = (0,0)$
.
In this setting, the local theory of Theorem5.1 can be used to analyze the monodromy of the family
around the boundary
![]() $\partial D^*$
.
$\partial D^*$
.
Theorem 5.2 (Picard–Lefschetz for plane curve families). Let
![]() $f \in{\mathbb{C}} P^N$
satisfy the properties (1), (2), (3) listed above. Let
$f \in{\mathbb{C}} P^N$
satisfy the properties (1), (2), (3) listed above. Let
![]() $X = V(z^d - f(x,y,z))$
denote the fiber above
$X = V(z^d - f(x,y,z))$
denote the fiber above
![]() $1 \in D^*$
. Then there is a vanishing cycle
$1 \in D^*$
. Then there is a vanishing cycle
![]() $c \subset X$
so that the monodromy
$c \subset X$
so that the monodromy
![]() $\mu \in \textrm{Mod}(X)$
obtained by traversing
$\mu \in \textrm{Mod}(X)$
obtained by traversing
![]() $\partial D^*$
counter-clockwise is given by a right-handed Dehn twist about the vanishing cycle:
$\partial D^*$
counter-clockwise is given by a right-handed Dehn twist about the vanishing cycle:
Proof. Condition (2) asserts that the monodromy can be computed by restricting attention to the affine subfamily obtained by setting
![]() $z = 1$
. Define
$z = 1$
. Define
Define
![]() $U = \{(x,y) \in{\mathbb{C}}^2 \mid \left |{f(x,y,1)}\right | \le 1\}$
and consider
$U = \{(x,y) \in{\mathbb{C}}^2 \mid \left |{f(x,y,1)}\right | \le 1\}$
and consider
![]() $f(x,y,1)$
as a holomorphic function
$f(x,y,1)$
as a holomorphic function
![]() $f: U \to D$
. The monodromy of this family then corresponds to the monodromy of the original family
$f: U \to D$
. The monodromy of this family then corresponds to the monodromy of the original family
![]() $E \to D^*$
. The result now follows from Condition (3) in combination with Theorem5.1 as applied to
$E \to D^*$
. The result now follows from Condition (3) in combination with Theorem5.1 as applied to
![]() $f(x,y,1)$
.
$f(x,y,1)$
.
5.2. Lönne’s theorem
There are some preliminary notions to establish before Lönne’s theorem can be stated. We begin by introducing the Lönne graphs
![]() $\Gamma _d$
. Lönne obtains his presentation of
$\Gamma _d$
. Lönne obtains his presentation of
![]() $\pi _1(\mathcal{P}_d)$
as a quotient a certain group constructed from
$\pi _1(\mathcal{P}_d)$
as a quotient a certain group constructed from
![]() $\Gamma _d$
.
$\Gamma _d$
.
Definition 5.3.
[Lönne graph] Let
![]() $d \ge 3$
be given. The Lönne graph
$d \ge 3$
be given. The Lönne graph
![]() $\Gamma _d$
has vertex set
$\Gamma _d$
has vertex set
Vertices
![]() $(a_1,b_1)$
and
$(a_1,b_1)$
and
![]() $(a_2, b_2)$
are connected by an edge if and only if both of the following conditions are met:
$(a_2, b_2)$
are connected by an edge if and only if both of the following conditions are met:
-
1.
 $\left |{a_1-a_2}\right | \le 1$
and
$\left |{a_1-a_2}\right | \le 1$
and
 $\left |{b_1-b_2}\right | \le 1$
.
$\left |{b_1-b_2}\right | \le 1$
. -
2.
 $(a_1-a_2)(b_1 - b_2) \le 0$
.
$(a_1-a_2)(b_1 - b_2) \le 0$
.
The set of edges of
![]() $\Gamma _d$
is denoted
$\Gamma _d$
is denoted
![]() $E_d$
.
$E_d$
.

Figure 3. The Lönne graph
![]() $\Gamma _5$
.
$\Gamma _5$
.
Vertices
![]() $i,j,k \in \Gamma _d$
are said to form a triangle when
$i,j,k \in \Gamma _d$
are said to form a triangle when
![]() $i,j,k$
are mutually adjacent. The triangles in the Lönne graph are crucial to what follows. It will be necessary to endow them with orientations.
$i,j,k$
are mutually adjacent. The triangles in the Lönne graph are crucial to what follows. It will be necessary to endow them with orientations.
Definition 5.4 (Orientation of triangles). Let
![]() $i,j,k$
determine a triangle in
$i,j,k$
determine a triangle in
![]() $\Gamma _d$
.
$\Gamma _d$
.
-
1. If
then the triangle \begin{equation*} i = (a,b),\quad j= (a,b+1), \quad k = (a+1,b), \end{equation*}
\begin{equation*} i = (a,b),\quad j= (a,b+1), \quad k = (a+1,b), \end{equation*}
 $i,j,k$
is positively-oriented by traversing the boundary clockwise.
$i,j,k$
is positively-oriented by traversing the boundary clockwise.
-
2. If
then the triangle \begin{equation*} i = (a,b), \quad j = (a,b+1), \quad k = (a-1,b+1), \end{equation*}
\begin{equation*} i = (a,b), \quad j = (a,b+1), \quad k = (a-1,b+1), \end{equation*}
 $i,j,k$
is positively oriented by traversing the boundary counterclockwise.
$i,j,k$
is positively oriented by traversing the boundary counterclockwise.
We say that the ordered triple
![]() $(i,j,k)$
of vertices determining a triangle is positively oriented if traversing the boundary from
$(i,j,k)$
of vertices determining a triangle is positively oriented if traversing the boundary from
![]() $i$
to
$i$
to
![]() $j$
to
$j$
to
![]() $k$
agrees with the orientation specified above.
$k$
agrees with the orientation specified above.
Definition 5.5 (Artin group). Let
![]() $\Gamma$
be a graph with vertex set
$\Gamma$
be a graph with vertex set
![]() $V$
and edge set
$V$
and edge set
![]() $E$
. The Artin group
$E$
. The Artin group
![]() $A(\Gamma )$
is defined to be the group with generators
$A(\Gamma )$
is defined to be the group with generators
subject to the following relations:
-
1.
 $\sigma _i \sigma _j = \sigma _j \sigma _i$
for all
$\sigma _i \sigma _j = \sigma _j \sigma _i$
for all
 $(i,j) \not \in E$
.
$(i,j) \not \in E$
. -
2.
 $\sigma _i \sigma _j \sigma _i = \sigma _j \sigma _i \sigma _j$
for all
$\sigma _i \sigma _j \sigma _i = \sigma _j \sigma _i \sigma _j$
for all
 $(i,j) \in E$
.
$(i,j) \in E$
.
Theorem 5.6 (Lönne). For
![]() $d \ge 3$
, the group
$d \ge 3$
, the group
![]() $\pi _1(\mathcal{P}_d)$
is isomorphic to a quotient of the Artin group
$\pi _1(\mathcal{P}_d)$
is isomorphic to a quotient of the Artin group
![]() $A(\Gamma _d)$
, subject to the following additional relations:
$A(\Gamma _d)$
, subject to the following additional relations:
-
3.
 $\sigma _i \sigma _j \sigma _k \sigma _i = \sigma _j \sigma _k \sigma _i \sigma _j$
if
$\sigma _i \sigma _j \sigma _k \sigma _i = \sigma _j \sigma _k \sigma _i \sigma _j$
if
 $(i,j,k)$
forms a positively-oriented triangle in
$(i,j,k)$
forms a positively-oriented triangle in
 $\Gamma _d$
.
$\Gamma _d$
. -
4. An additional family of relations
 $R_i, i \in I_d$
.
$R_i, i \in I_d$
. -
5. An additional relation
 $\widetilde R$
.
$\widetilde R$
.
Remark 5.7.
Define the group
![]() $B(\Gamma _d)$
as the quotient of the Artin group
$B(\Gamma _d)$
as the quotient of the Artin group
![]() $A(\Gamma _d)$
by the family of relations (
3
) in Theorem
5.6
. As our statement of Lönne’s theorem indicates, the additional relations will be of no use to us, and our theorem really concerns the lift of the monodromy representation
$A(\Gamma _d)$
by the family of relations (
3
) in Theorem
5.6
. As our statement of Lönne’s theorem indicates, the additional relations will be of no use to us, and our theorem really concerns the lift of the monodromy representation
![]() $\tilde \rho _d: B(\Gamma _d) \to \textrm{Mod}(\Sigma _g)$
.
$\tilde \rho _d: B(\Gamma _d) \to \textrm{Mod}(\Sigma _g)$
.
For the analysis to follow, it is essential to understand the mapping classes
![]() $\rho _d(\sigma _i), i \in I_d$
.
$\rho _d(\sigma _i), i \in I_d$
.
Proposition 5.8.
For each generator
![]() $\sigma _i$
of Theorem
5.6
, the image
$\sigma _i$
of Theorem
5.6
, the image
is a right-handed Dehn twist about some vanishing cycle
![]() $c_i$
on a fiber
$c_i$
on a fiber
![]() $X \in \mathcal{P}_d$
.
$X \in \mathcal{P}_d$
.
Proof. The result will follow from Theorem 5.2, once certain aspects of Lönne’s proof are recalled.
The generators
![]() $\sigma _i$
of Theorem 5.6 correspond to specific loops in
$\sigma _i$
of Theorem 5.6 correspond to specific loops in
![]() $\mathcal{P}_d$
known as geometric elements.
$\mathcal{P}_d$
known as geometric elements.
Definition 5.9 (Geometric element). Let
![]() $D = V(p)$
be a hypersurface in
$D = V(p)$
be a hypersurface in
![]() ${\mathbb{C}}^n$
defined by some polynomial
${\mathbb{C}}^n$
defined by some polynomial
![]() $p$
. An element
$p$
. An element
![]() $x \in \pi _1({\mathbb{C}}^n \setminus D)$
that can be represented by a path isotopic to the boundary of a small disk transversal to
$x \in \pi _1({\mathbb{C}}^n \setminus D)$
that can be represented by a path isotopic to the boundary of a small disk transversal to
![]() $D$
is called a geometric element. If
$D$
is called a geometric element. If
![]() $\widetilde D$
is a projective hypersurface, an element
$\widetilde D$
is a projective hypersurface, an element
![]() $x \in \pi _1({\mathbb{C}} P^n \setminus \widetilde D)$
is said to be a geometric element if it can be represented by a geometric element in some affine chart.
$x \in \pi _1({\mathbb{C}} P^n \setminus \widetilde D)$
is said to be a geometric element if it can be represented by a geometric element in some affine chart.
In Lönne’s terminology, the generators
![]() $\sigma _i, i \in I_d$
arise as a “Hefez-Lazzeri basis”—this will require some explanation. Consider the linearly perturbed Fermat polynomial
$\sigma _i, i \in I_d$
arise as a “Hefez-Lazzeri basis”—this will require some explanation. Consider the linearly perturbed Fermat polynomial
for well-chosen constants
![]() $\nu _x, \nu _y$
. Such an
$\nu _x, \nu _y$
. Such an
![]() $f$
satisfies the conditions (1)–(3) of Theorem5.2 near each critical point. Moreover, there is a bijection between the critical points of
$f$
satisfies the conditions (1)–(3) of Theorem5.2 near each critical point. Moreover, there is a bijection between the critical points of
![]() $f(x,y,1)$
and the set
$f(x,y,1)$
and the set
![]() $I_d$
of Definition 5.3. If
$I_d$
of Definition 5.3. If
![]() $\nu _x, \nu _y$
are chosen carefully, each critical point lies above a distinct critical value - in this way we embed
$\nu _x, \nu _y$
are chosen carefully, each critical point lies above a distinct critical value - in this way we embed
![]() $I_d \subset{\mathbb{C}}$
.
$I_d \subset{\mathbb{C}}$
.
Each
![]() $c \in{\mathbb{C}}$
determines a plane curve
$c \in{\mathbb{C}}$
determines a plane curve
![]() $V(cz^d-f)$
. The values of
$V(cz^d-f)$
. The values of
![]() $c$
for which
$c$
for which
![]() $V(c z^d-f)$
is not smooth are exactly the critical values of
$V(c z^d-f)$
is not smooth are exactly the critical values of
![]() $f(x,y,1)$
. The family
$f(x,y,1)$
. The family
is a subfamily of
![]() $\mathcal{P}_{d}$
defined over
$\mathcal{P}_{d}$
defined over
![]() ${\mathbb{C}} \setminus I_d$
. The Hefez–Lazzeri basis
${\mathbb{C}} \setminus I_d$
. The Hefez–Lazzeri basis
![]() $\{\sigma _i \mid i \in I_d\}$
is a carefully chosen set of paths in
$\{\sigma _i \mid i \in I_d\}$
is a carefully chosen set of paths in
![]() ${\mathbb{C}} \setminus I_d$
with each
${\mathbb{C}} \setminus I_d$
with each
![]() $\sigma _i$
encircling an individual
$\sigma _i$
encircling an individual
![]() $i \in I_d$
. Lönne shows that the inclusions of these paths into
$i \in I_d$
. Lönne shows that the inclusions of these paths into
![]() $\mathcal{P}_d$
via the family
$\mathcal{P}_d$
via the family
![]() $H$
generates
$H$
generates
![]() $\pi _1(\mathcal{P}_d)$
. The result now follows from an application of Theorem5.2.
$\pi _1(\mathcal{P}_d)$
. The result now follows from an application of Theorem5.2.
5.3. First properties of
 $\rho _d$
$\rho _d$
Proposition 5.8 establishes the existence of a collection
![]() $c_i, i \in I_d$
of vanishing cycles on
$c_i, i \in I_d$
of vanishing cycles on
![]() $X$
. In this section, we derive some basic topological properties of this configuration arising from the fact that the Dehn twists
$X$
. In this section, we derive some basic topological properties of this configuration arising from the fact that the Dehn twists
![]() $T_{c_i}^{-1}$
must satisfy the relations (1)-(3) of Lönne’s presentation.
$T_{c_i}^{-1}$
must satisfy the relations (1)-(3) of Lönne’s presentation.
Lemma 5.10.
-
1. If the vertices
 $v_i, v_j$
are adjacent, then the curves
$v_i, v_j$
are adjacent, then the curves
 $c_i, c_j$
satisfy
$c_i, c_j$
satisfy
 $i(c_i, c_j) = 1$
.
$i(c_i, c_j) = 1$
. -
2. For
 $d \ge 4$
, the curves
$d \ge 4$
, the curves
 $c_i, i \in I_d$
are pairwise distinct, and all
$c_i, i \in I_d$
are pairwise distinct, and all
 $c_i$
are non-separating.
$c_i$
are non-separating.
-
3. If the vertices
 $v_i, v_j$
in
$v_i, v_j$
in
 $\Gamma _d$
are non-adjacent, then the curves
$\Gamma _d$
are non-adjacent, then the curves
 $c_i$
and
$c_i$
and
 $c_j$
are disjoint.
$c_j$
are disjoint.
-
4. For
 $d \ge 4$
, if the vertices
$d \ge 4$
, if the vertices
 $v_i, v_j, v_k$
form a triangle in
$v_i, v_j, v_k$
form a triangle in
 $\Gamma _d$
, then the curves
$\Gamma _d$
, then the curves
 $c_i, c_j, c_k$
are supported on an essential subsurface
Footnote 5
$c_i, c_j, c_k$
are supported on an essential subsurface
Footnote 5
 $S_{ijk} \subset X$
homeomorphic to
$S_{ijk} \subset X$
homeomorphic to
 $\Sigma _{1,2}$
. Moreover, if the triangle determined by
$\Sigma _{1,2}$
. Moreover, if the triangle determined by
 $v_i,v_j,v_k$
is positively oriented, then
$v_i,v_j,v_k$
is positively oriented, then
 $i(c_i, T^{-1}_{c_j}(c_k)) = 0$
.
$i(c_i, T^{-1}_{c_j}(c_k)) = 0$
.
Proof. (1): If
![]() $v_i$
and
$v_i$
and
![]() $v_j$
are adjacent, then the Dehn twists
$v_j$
are adjacent, then the Dehn twists
![]() $T_{c_i}^{-1}$
and
$T_{c_i}^{-1}$
and
![]() $T_{c_j}^{-1}$
satisfy the braid relation. It follows from Proposition 4.3 that
$T_{c_j}^{-1}$
satisfy the braid relation. It follows from Proposition 4.3 that
![]() $i(c_i,c_j) = 1$
.
$i(c_i,c_j) = 1$
.
(2): Suppose
![]() $v_i$
and
$v_i$
and
![]() $v_j$
are distinct vertices. For
$v_j$
are distinct vertices. For
![]() $d \ge 4$
, no two vertices have the same set of adjacent vertices, so that there is some
$d \ge 4$
, no two vertices have the same set of adjacent vertices, so that there is some
![]() $v_k$
adjacent to
$v_k$
adjacent to
![]() $v_i$
and not
$v_i$
and not
![]() $v_j$
. By (1) above, it follows that
$v_j$
. By (1) above, it follows that
![]() $T_{c_i}^{-1}$
and
$T_{c_i}^{-1}$
and
![]() $T_{c_k}^{-1}$
satisfy the braid relation, while
$T_{c_k}^{-1}$
satisfy the braid relation, while
![]() $T_{c_j}^{-1}$
and
$T_{c_j}^{-1}$
and
![]() $T_{c_k}^{-1}$
do not, showing that the isotopy classes of
$T_{c_k}^{-1}$
do not, showing that the isotopy classes of
![]() $c_i$
and
$c_i$
and
![]() $c_j$
are distinct. Since each
$c_j$
are distinct. Since each
![]() $c_i$
satisfies a braid relation with some other
$c_i$
satisfies a braid relation with some other
![]() $c_j$
, Proposition 4.3 shows that
$c_j$
, Proposition 4.3 shows that
![]() $c_i$
is non-separating.
$c_i$
is non-separating.
(3): If
![]() $v_i$
and
$v_i$
and
![]() $v_j$
are non-adjacent, then the Dehn twists
$v_j$
are non-adjacent, then the Dehn twists
![]() $T_{c_i}^{-1}$
and
$T_{c_i}^{-1}$
and
![]() $T_{c_j}^{-1}$
commute. According to [ [Reference Farb and Margalit13], Section 3.5.2], this implies that either
$T_{c_j}^{-1}$
commute. According to [ [Reference Farb and Margalit13], Section 3.5.2], this implies that either
![]() $c_i = c_j$
or else
$c_i = c_j$
or else
![]() $c_i$
and
$c_i$
and
![]() $c_j$
are disjoint. By (2), the former possibility cannot hold.
$c_j$
are disjoint. By (2), the former possibility cannot hold.
(4): Via the change-of-coordinates principle, it can be checked that if
![]() $c_i, c_j, c_k$
are curves that pairwise intersect once, then
$c_i, c_j, c_k$
are curves that pairwise intersect once, then
![]() $c_i \cup c_j \cup c_k$
is supported on an essential subsurface of the form
$c_i \cup c_j \cup c_k$
is supported on an essential subsurface of the form
![]() $\Sigma _{1,b}$
for
$\Sigma _{1,b}$
for
![]() $1 \le b \le 3$
. In the case
$1 \le b \le 3$
. In the case
![]() $b = 1$
, the curve
$b = 1$
, the curve
![]() $c_k$
must be of the form
$c_k$
must be of the form
![]() $c_k = T_{c_i}^{\pm 1}(c_j)$
. It follows that if
$c_k = T_{c_i}^{\pm 1}(c_j)$
. It follows that if
![]() $d$
is a curve such that
$d$
is a curve such that
![]() $i(d,c_k) \ne 0$
, then at least one of
$i(d,c_k) \ne 0$
, then at least one of
![]() $i(d, c_i)$
and
$i(d, c_i)$
and
![]() $i(d,c_j)$
must also be nonzero. However, as
$i(d,c_j)$
must also be nonzero. However, as
![]() $d \ge 4$
, there is always some vertex
$d \ge 4$
, there is always some vertex
![]() $v_l$
adjacent to exactly one of
$v_l$
adjacent to exactly one of
![]() $c_i, c_j, c_k$
. The corresponding curve
$c_i, c_j, c_k$
. The corresponding curve
![]() $c_l$
would violate the condition required of
$c_l$
would violate the condition required of
![]() $d$
above (possibly after permuting the indices
$d$
above (possibly after permuting the indices
![]() $i,j,k$
).
$i,j,k$
).
It remains to eliminate the possibility
![]() $b = 3$
. In this case, the change-of-coordinates principle implies that up to homeomorphism, the curves
$b = 3$
. In this case, the change-of-coordinates principle implies that up to homeomorphism, the curves
![]() $c_i, c_j, c_k$
must be arranged as in Figure 4. It can be checked directly (e.g., by examining the action on
$c_i, c_j, c_k$
must be arranged as in Figure 4. It can be checked directly (e.g., by examining the action on
![]() $H_1(\Sigma _{1,3})$
) that for this configuration, the relation
$H_1(\Sigma _{1,3})$
) that for this configuration, the relation
does not hold. This violates relation (3) in Lönne’s presentation of
![]() $\pi _1(\mathcal{P}_d)$
. We conclude that necessarily
$\pi _1(\mathcal{P}_d)$
. We conclude that necessarily
![]() $b = 2$
.
$b = 2$
.
Having shown that
![]() $b = 2$
, it remains to show the condition
$b = 2$
, it remains to show the condition
![]() $i(c_i, T^{-1}_{c_j}(c_k)) = 0$
for a positively oriented triangle. Let
$i(c_i, T^{-1}_{c_j}(c_k)) = 0$
for a positively oriented triangle. Let
![]() $(x,y,z)$
denote a
$(x,y,z)$
denote a
![]() $3$
-chain on
$3$
-chain on
![]() $\Sigma _{1,2}$
. The change-of-coordinates principle implies that without loss of generality,
$\Sigma _{1,2}$
. The change-of-coordinates principle implies that without loss of generality,
![]() $c_i=x, c_j=y$
, and
$c_i=x, c_j=y$
, and
![]() $c_k = T_y^{\pm 1}(z)$
. We wish to show that necessarily
$c_k = T_y^{\pm 1}(z)$
. We wish to show that necessarily
![]() $c_k = T_y(z)$
. It can be checked directly (e.g., by considering the action on
$c_k = T_y(z)$
. It can be checked directly (e.g., by considering the action on
![]() $H_1(\Sigma _{1,2})$
) that only in the case
$H_1(\Sigma _{1,2})$
) that only in the case
![]() $c_k = T_y(z)$
does relation (3) in the Lönne presentation hold.
$c_k = T_y(z)$
does relation (3) in the Lönne presentation hold.

Figure 4. Lemma 5.10.4: the configuration of
![]() $c_i,c_j,c_k$
in the
$c_i,c_j,c_k$
in the
![]() $b = 3$
case.
$b = 3$
case.
6. Configurations of vanishing cycles
The goal of this section is to derive an explicit picture of the configuration of vanishing cycles on a plane curve of degree
![]() $5$
. The main result of the section is Lemma 6.1.
$5$
. The main result of the section is Lemma 6.1.
Lemma 6.1.
There is a homeomorphism
![]() $f: X \to \Sigma _6$
such that with reference to Figure
5
,
$f: X \to \Sigma _6$
such that with reference to Figure
5
,
-
1. The curves
 $c_1, \dots, c_{12}$
are vanishing cycles; that is,
$c_1, \dots, c_{12}$
are vanishing cycles; that is,
 $T_{c_i} \in \mathrm{Im}(\rho _5)$
for
$T_{c_i} \in \mathrm{Im}(\rho _5)$
for
 $1 \le i \le 12$
. The curves
$1 \le i \le 12$
. The curves
 $x,y,z$
are also vanishing cycles.
$x,y,z$
are also vanishing cycles.
-
2. The curve
 $b$
satisfies
$b$
satisfies
 $T_b^2 \in \mathrm{Im}(\rho _5)$
.
$T_b^2 \in \mathrm{Im}(\rho _5)$
.

Figure 5. The curves of Lemma 6.1. The bottom halves of curves
![]() $b,x,y,z,$
and
$b,x,y,z,$
and
![]() $c_i$
for
$c_i$
for
![]() $i$
odd have been omitted for clarity; on the bottom half, each curve follows its mirror image on the top.
$i$
odd have been omitted for clarity; on the bottom half, each curve follows its mirror image on the top.
Proof. Lemma 6.1 will be proved in three steps.
Step 1: Uniqueness of Lönne configurations
Lemma 6.2.
Suppose
![]() $d \ge 5$
is odd. Up to homeomorphism, there is a unique configuration of curves
$d \ge 5$
is odd. Up to homeomorphism, there is a unique configuration of curves
![]() $c_i, i \in I_d$
on
$c_i, i \in I_d$
on
![]() $\Sigma _g$
whose intersection pattern is prescribed by
$\Sigma _g$
whose intersection pattern is prescribed by
![]() $\Gamma _d$
and such that the twists
$\Gamma _d$
and such that the twists
![]() $T_{c_i}^{-1}$
satisfy the relations (1),(2),(3) given by Lönne’s presentation.
$T_{c_i}^{-1}$
satisfy the relations (1),(2),(3) given by Lönne’s presentation.
A configuration of curves
![]() $c_i, i \in I_d$
as in Lemma 6.2 will be referred to as a Lönne configuration.
$c_i, i \in I_d$
as in Lemma 6.2 will be referred to as a Lönne configuration.
Proof. Let
![]() $a_{1,1},\dots, a_{d-1, d-1}$
determine a Lönne configuration on
$a_{1,1},\dots, a_{d-1, d-1}$
determine a Lönne configuration on
![]() $\Sigma _g$
. We will exhibit a homeomorphism of
$\Sigma _g$
. We will exhibit a homeomorphism of
![]() $\Sigma _g$
taking each
$\Sigma _g$
taking each
![]() $a_{i,j}$
to a corresponding
$a_{i,j}$
to a corresponding
![]() $b_{i,j}$
in a “reference” configuration
$b_{i,j}$
in a “reference” configuration
![]() $\{b_{i,j}\}$
to be constructed in the course of the proof. This will require three steps.
$\{b_{i,j}\}$
to be constructed in the course of the proof. This will require three steps.
Step 1: A collection of disjoint chains
Each row in the Lönne graph determines a chain of length
![]() $d-1$
. The change of coordinates principle for chains of even length (Lemma 4.2) asserts that any two chains of length
$d-1$
. The change of coordinates principle for chains of even length (Lemma 4.2) asserts that any two chains of length
![]() $d-1$
are equivalent up to homeomorphism. Considering the odd-numbered rows of
$d-1$
are equivalent up to homeomorphism. Considering the odd-numbered rows of
![]() $\Gamma _d$
, it follows that there is a homeomorphism
$\Gamma _d$
, it follows that there is a homeomorphism
![]() $f_1$
of
$f_1$
of
![]() $\Sigma _g$
that takes each
$\Sigma _g$
that takes each
![]() $a_{2i-1,j}$
for
$a_{2i-1,j}$
for
![]() $1 \le i \le d-1$
to a curve
$1 \le i \le d-1$
to a curve
![]() $b_{2i-1,j}$
in a standard picture of a chain. We denote the subsurface of
$b_{2i-1,j}$
in a standard picture of a chain. We denote the subsurface of
![]() $\Sigma _g$
determined by the chain
$\Sigma _g$
determined by the chain
![]() $a_{2i-1,1}, \dots, a_{2i-1,d-1}$
as
$a_{2i-1,1}, \dots, a_{2i-1,d-1}$
as
![]() $A_i$
, and similarly we define the subsurfaces
$A_i$
, and similarly we define the subsurfaces
![]() $B_i$
of the reference configuration. Each
$B_i$
of the reference configuration. Each
![]() $A_i, B_i$
is homeomorphic to
$A_i, B_i$
is homeomorphic to
![]() $\Sigma _{(d-1)/2,1}$
.
$\Sigma _{(d-1)/2,1}$
.
Step 2: Arcs on
![]() $A_i$
$A_i$
The next step is to show that up to homeomorphism, there is a unique picture of what the intersection of the remaining curves
![]() $a_{2i,j}$
with
$a_{2i,j}$
with
![]() $\bigcup A_i$
looks like. Consider a curve
$\bigcup A_i$
looks like. Consider a curve
![]() $a_{2i,j}$
. Up to isotopy,
$a_{2i,j}$
. Up to isotopy,
![]() $a_{2i,j}$
intersects only the subsurfaces
$a_{2i,j}$
intersects only the subsurfaces
![]() $A_i$
and
$A_i$
and
![]() $A_{i+1}$
. We claim that
$A_{i+1}$
. We claim that
![]() $a_{2i,j}$
can be isotoped so that its intersection with
$a_{2i,j}$
can be isotoped so that its intersection with
![]() $A_i$
is a single arc, and similarly for
$A_i$
is a single arc, and similarly for
![]() $A_{i+1}$
. If
$A_{i+1}$
. If
![]() $j = d-1$
, then
$j = d-1$
, then
![]() $a_{2i, d-1}$
intersects only the curve
$a_{2i, d-1}$
intersects only the curve
![]() $a_{2i-1, d-1}$
, and
$a_{2i-1, d-1}$
, and
![]() $i(a_{2i,d-1},a_{2i-1,d-1}) = 1$
. It follows that if
$i(a_{2i,d-1},a_{2i-1,d-1}) = 1$
. It follows that if
![]() $a_{2i,d-1} \cap A_i$
has multiple components, exactly one is essential, and the remaining components can be isotoped off of
$a_{2i,d-1} \cap A_i$
has multiple components, exactly one is essential, and the remaining components can be isotoped off of
![]() $A_i$
.
$A_i$
.
In the general case, where
![]() $a_{2i,j}$
intersects both
$a_{2i,j}$
intersects both
![]() $a_{2i-1,j}$
and
$a_{2i-1,j}$
and
![]() $a_{2i-1,j+1}$
, an analogous argument shows that
$a_{2i-1,j+1}$
, an analogous argument shows that
![]() $a_{2i,j} \cap A_i$
consists of one or two essential arcs. Consider the triangle in the Lönne graph determined by
$a_{2i,j} \cap A_i$
consists of one or two essential arcs. Consider the triangle in the Lönne graph determined by
![]() $a_{2i,j}, a_{2i-1,j}, a_{2i-1, j+1}$
. According to Lemma 5.10.4, the union
$a_{2i,j}, a_{2i-1,j}, a_{2i-1, j+1}$
. According to Lemma 5.10.4, the union
![]() $a_{2i,j}\cup a_{2i-1,j}\cup a_{2i-1, j+1}$
is supported on an essential subsurface of the form
$a_{2i,j}\cup a_{2i-1,j}\cup a_{2i-1, j+1}$
is supported on an essential subsurface of the form
![]() $\Sigma _{1,2}$
. Figure 6 shows that if
$\Sigma _{1,2}$
. Figure 6 shows that if
![]() $a_{2i,j} \cap A_i$
consists of two essential arcs, then
$a_{2i,j} \cap A_i$
consists of two essential arcs, then
![]() $a_{2i,j}\cup a_{2i-1,j}\cup a_{2i-1, j+1}$
is supported on an essential subsurface of the form
$a_{2i,j}\cup a_{2i-1,j}\cup a_{2i-1, j+1}$
is supported on an essential subsurface of the form
![]() $\Sigma _{1,3}$
, in contradiction with Lemma 5.10.4. Similar arguments establish that
$\Sigma _{1,3}$
, in contradiction with Lemma 5.10.4. Similar arguments establish that
![]() $a_{2i-2,j} \cap A_{i}$
is a single essential arc as well.
$a_{2i-2,j} \cap A_{i}$
is a single essential arc as well.

Figure 6. If
![]() $a_{2i,j}$
cannot be isotoped onto a single arc inside
$a_{2i,j}$
cannot be isotoped onto a single arc inside
![]() $A_i$
, then the curve enclosed by the inner strip (shaded) is essential in
$A_i$
, then the curve enclosed by the inner strip (shaded) is essential in
![]() $\Sigma _g$
, causing
$\Sigma _g$
, causing
![]() $a_{2i,j}\cup a_{2i-1,j}\cup a_{2i-1, j+1}$
to be supported on a surface
$a_{2i,j}\cup a_{2i-1,j}\cup a_{2i-1, j+1}$
to be supported on a surface
![]() $\Sigma _{1,3}$
.
$\Sigma _{1,3}$
.
We next show that all points of intersection
![]() $a_{2i,j} \cap a_{2i, j +1}$
can be isotoped to occur on both
$a_{2i,j} \cap a_{2i, j +1}$
can be isotoped to occur on both
![]() $A_i$
and
$A_i$
and
![]() $A_{i+1}$
. This also follows from Lemma 5.10.4. If some point of intersection
$A_{i+1}$
. This also follows from Lemma 5.10.4. If some point of intersection
![]() $a_{2i,j} \cap a_{2i, j +1}$
could not be isotoped onto
$a_{2i,j} \cap a_{2i, j +1}$
could not be isotoped onto
![]() $A_i$
, then the union
$A_i$
, then the union
![]() $a_{2i, j} \cup a_{2i, j+1} \cup a_{2i-1, j+1}$
could not be supported on a subsurface homeomorphic to
$a_{2i, j} \cup a_{2i, j+1} \cup a_{2i-1, j+1}$
could not be supported on a subsurface homeomorphic to
![]() $\Sigma _{1,2}$
. An analogous argument applies with
$\Sigma _{1,2}$
. An analogous argument applies with
![]() $A_{i+1}$
in place of
$A_{i+1}$
in place of
![]() $A_i$
. This is explained in Figure 7.
$A_i$
. This is explained in Figure 7.

Figure 7. If the intersection
![]() $a_{2i,j} \cap a_{2i,j+1}$
cannot be isotoped to occur on
$a_{2i,j} \cap a_{2i,j+1}$
cannot be isotoped to occur on
![]() $A_i$
, then both curves indicated by the shaded regions are essential in
$A_i$
, then both curves indicated by the shaded regions are essential in
![]() $\Sigma _g$
, causing
$\Sigma _g$
, causing
![]() $a_{2i,j}\cup a_{2i,j+1}\cup a_{2i-1, j+1}$
to be supported on a surface
$a_{2i,j}\cup a_{2i,j+1}\cup a_{2i-1, j+1}$
to be supported on a surface
![]() $\Sigma _{1,3}$
.
$\Sigma _{1,3}$
.
It follows from this analysis that all crossings between curves in row
![]() $2i$
can be isotoped to occur in a collar neighborhood of
$2i$
can be isotoped to occur in a collar neighborhood of
![]() $\partial A_i$
. We define
$\partial A_i$
. We define
![]() $A_i^+$
to be a slight enlargement of
$A_i^+$
to be a slight enlargement of
![]() $A_i$
along such a neighborhood, so that all crossings between curves in row
$A_i$
along such a neighborhood, so that all crossings between curves in row
![]() $2i$
occur in
$2i$
occur in
![]() $A_i^+ \setminus A_i$
.
$A_i^+ \setminus A_i$
.
We can now understand what the collection of arcs
![]() $a_{2i,1} \cap A_i^+, \dots, a_{2i, d-1}\cap A_i^+$
looks like. To begin with, the change-of-coordinates principle asserts that up to a homeomorphism of
$a_{2i,1} \cap A_i^+, \dots, a_{2i, d-1}\cap A_i^+$
looks like. To begin with, the change-of-coordinates principle asserts that up to a homeomorphism of
![]() $A_i$
fixing the curves
$A_i$
fixing the curves
![]() $\{a_{2i-1,j}\}$
, the arc
$\{a_{2i-1,j}\}$
, the arc
![]() $a_{2i,1} \cap A_i$
can be drawn in one of two ways. The first possibility is shown in Figure 8(a), and the second is its mirror-image obtained by reflection through the plane of the page (i.e., the curve with the dotted and solid portions exchanged). In fact,
$a_{2i,1} \cap A_i$
can be drawn in one of two ways. The first possibility is shown in Figure 8(a), and the second is its mirror-image obtained by reflection through the plane of the page (i.e., the curve with the dotted and solid portions exchanged). In fact,
![]() $a_{2i,1} \cap A_i$
must look as shown. This follows from Lemma 5.10.4. The vertices
$a_{2i,1} \cap A_i$
must look as shown. This follows from Lemma 5.10.4. The vertices
![]() $(a_{2i-1, 1}, a_{2i-1, 2}, a_{2i,1})$
form a positively oriented triangle, and so
$(a_{2i-1, 1}, a_{2i-1, 2}, a_{2i,1})$
form a positively oriented triangle, and so
![]() $i(a_{2i-1,1}, T_{a_{2i-1,2}}^{-1}(a_{2i,1})) = 0$
. This condition precludes the other possibility.
$i(a_{2i-1,1}, T_{a_{2i-1,2}}^{-1}(a_{2i,1})) = 0$
. This condition precludes the other possibility.
The pictures for
![]() $a_{2i,2}, \dots, a_{2i, d-1}$
are obtained by proceeding inductively. In each case, there are exactly two ways to draw an arc satisfying the requisite intersection properties, and Lemma 5.10.4 precludes one of these possibilities. The result is shown in Figure 8(b).
$a_{2i,2}, \dots, a_{2i, d-1}$
are obtained by proceeding inductively. In each case, there are exactly two ways to draw an arc satisfying the requisite intersection properties, and Lemma 5.10.4 precludes one of these possibilities. The result is shown in Figure 8(b).
It remains to understand how the crossings between curves in row
![]() $2i$
are organized on
$2i$
are organized on
![]() $A_i^+$
. As shown, the arcs
$A_i^+$
. As shown, the arcs
![]() $a_{2i,j}\cap A_i$
and
$a_{2i,j}\cap A_i$
and
![]() $a_{2i,j+1}\cap A_i$
intersect
$a_{2i,j+1}\cap A_i$
intersect
![]() $\partial A_i$
twice each, and in both instances, the intersections are adjacent relative to the other arcs. There are thus apparently two possibilities for where the crossing can occur. However, one can see from Figure 8(c) that once a choice is made for one crossing, this enforces choices for the remaining crossings. Moreover, the two apparently distinct configurations are in fact equivalent: the cyclic ordering of the arcs along
$\partial A_i$
twice each, and in both instances, the intersections are adjacent relative to the other arcs. There are thus apparently two possibilities for where the crossing can occur. However, one can see from Figure 8(c) that once a choice is made for one crossing, this enforces choices for the remaining crossings. Moreover, the two apparently distinct configurations are in fact equivalent: the cyclic ordering of the arcs along
![]() $\partial A_i^+$
is the same in either case, and the combinatorial type of the cut-up surface
$\partial A_i^+$
is the same in either case, and the combinatorial type of the cut-up surface
is the same in either situation. The change-of-coordinates principle then asserts the existence of a homeomorphism of
![]() $A_i^+$
sending each
$A_i^+$
sending each
![]() $a_{2i-1,j}$
to itself and taking one configuration of arcs to the other.
$a_{2i-1,j}$
to itself and taking one configuration of arcs to the other.
Having seen that the arcs
![]() $a_{2i,j} \cap A_i^+$
can be put into standard form, it remains to examine the other collection of arcs on
$a_{2i,j} \cap A_i^+$
can be put into standard form, it remains to examine the other collection of arcs on
![]() $A_i^+$
, namely those of the form
$A_i^+$
, namely those of the form
![]() $a_{2i-2,j}$
. It is easy to see by induction on
$a_{2i-2,j}$
. It is easy to see by induction on
![]() $d$
that the cut-up surface
$d$
that the cut-up surface
![]() $A_i^\circ$
is a union of polyhedral disks for which the edges correspond to portions of the curves
$A_i^\circ$
is a union of polyhedral disks for which the edges correspond to portions of the curves
![]() $a_{2i-1,j}$
, the arcs
$a_{2i-1,j}$
, the arcs
![]() $a_{2i,j} \cap A_i^+$
, or else the boundary
$a_{2i,j} \cap A_i^+$
, or else the boundary
![]() $\partial A_i^+$
. It follows that the isotopy class of an arc
$\partial A_i^+$
. It follows that the isotopy class of an arc
![]() $a_{2i-2,j}\cap A_I^+$
is uniquely determined by its intersection data with the curves
$a_{2i-2,j}\cap A_I^+$
is uniquely determined by its intersection data with the curves
![]() $a_{2i-1,j}$
and
$a_{2i-1,j}$
and
![]() $a_{2i,j}$
.
$a_{2i,j}$
.
For
![]() $j \ge 2$
, the curve
$j \ge 2$
, the curve
![]() $a_{2i-2,j}$
intersects
$a_{2i-2,j}$
intersects
![]() $a_{2i-1,j-1}$
and
$a_{2i-1,j-1}$
and
![]() $a_{2i-1,j}$
and is disjoint from all curves
$a_{2i-1,j}$
and is disjoint from all curves
![]() $a_{2i, k}$
. As
$a_{2i, k}$
. As
![]() $a_{2i,j-1}$
has the same set of intersections as
$a_{2i,j-1}$
has the same set of intersections as
![]() $a_{2i-2,j}$
, it follows that
$a_{2i-2,j}$
, it follows that
![]() $a_{2i-2,j} \cap A_i^+$
must run parallel to
$a_{2i-2,j} \cap A_i^+$
must run parallel to
![]() $a_{2i,j-1}$
. The curve
$a_{2i,j-1}$
. The curve
![]() $a_{2i-2,1}$
intersects only
$a_{2i-2,1}$
intersects only
![]() $a_{2i,1}$
; consequently,
$a_{2i,1}$
; consequently,
![]() $a_{2i-2,1}\cap A_i^+$
is uniquely determined. As can be seen from Figure 8(c), this forces each subsequent
$a_{2i-2,1}\cap A_i^+$
is uniquely determined. As can be seen from Figure 8(c), this forces each subsequent
![]() $a_{2i-2,j}$
onto a particular side of
$a_{2i-2,j}$
onto a particular side of
![]() $a_{2i,j-1}$
.
$a_{2i,j-1}$
.

Figure 8. The surface
![]() $A_i^+$
. (a): The correct choice for
$A_i^+$
. (a): The correct choice for
![]() $a_{2i,1} \cap A_i$
. (b): The configuration
$a_{2i,1} \cap A_i$
. (b): The configuration
![]() $a_{2i,j} \cap A_i$
. (c) The configuration
$a_{2i,j} \cap A_i$
. (c) The configuration
![]() $a_{2i,j} \cap A_i^+$
.
$a_{2i,j} \cap A_i^+$
.
Step 3: Arcs on the remainder of
![]() $\Sigma _g$
$\Sigma _g$
Consider now the subsurface
This has
![]() $(d-1)/2$
boundary components
$(d-1)/2$
boundary components
![]() $\partial _{k}$
, indexed by the corresponding
$\partial _{k}$
, indexed by the corresponding
![]() $A_k$
. The intersection
$A_k$
. The intersection
![]() $a_{2i,j} \cap \left ( \Sigma _g \setminus \bigcup A_i\right )$
consists of two arcs, each connecting
$a_{2i,j} \cap \left ( \Sigma _g \setminus \bigcup A_i\right )$
consists of two arcs, each connecting
![]() $\partial _{i}$
with
$\partial _{i}$
with
![]() $\partial _{i+1}$
. The strategy for the remainder of the proof is to argue that when all these arcs are deleted from
$\partial _{i+1}$
. The strategy for the remainder of the proof is to argue that when all these arcs are deleted from
![]() $\Sigma _g^\circ$
, the result is a union of disks. The change-of-coordinates principle will then assert the uniqueness of such a configuration of arcs, completing the proof.
$\Sigma _g^\circ$
, the result is a union of disks. The change-of-coordinates principle will then assert the uniqueness of such a configuration of arcs, completing the proof.
For what follows, it will be convenient to refer to a product neighborhood
![]() $[0,1] \times [0,1] \subset \Sigma _g^\circ$
of some arc
$[0,1] \times [0,1] \subset \Sigma _g^\circ$
of some arc
![]() $a_{2i,j} \cap \Sigma _g^\circ$
as a strip. Our first objective is to compute the Euler characteristic
$a_{2i,j} \cap \Sigma _g^\circ$
as a strip. Our first objective is to compute the Euler characteristic
![]() $\chi$
of the surface
$\chi$
of the surface
![]() $\Sigma _g^{\circ \circ }$
obtained by deleting strips for all arcs from
$\Sigma _g^{\circ \circ }$
obtained by deleting strips for all arcs from
![]() $\Sigma _g^\circ$
. Then an analysis of the pattern by which strips are attached will determine the number of components of this surface.
$\Sigma _g^\circ$
. Then an analysis of the pattern by which strips are attached will determine the number of components of this surface.
To begin, we return to the setting of Figure 7. Above, it was argued that for
![]() $2i \lt (d-1)/2$
, the intersection
$2i \lt (d-1)/2$
, the intersection
![]() $a_{2i,j} \cap a_{2i,j+1}$
can be isotoped onto either
$a_{2i,j} \cap a_{2i,j+1}$
can be isotoped onto either
![]() $A_{i}$
or
$A_{i}$
or
![]() $A_{i+1}$
. This means that there is a strip that contains both
$A_{i+1}$
. This means that there is a strip that contains both
![]() $a_{2i,j} \cap \Sigma _g^\circ$
and
$a_{2i,j} \cap \Sigma _g^\circ$
and
![]() $a_{2i,j+1} \cap \Sigma _g^\circ$
. Grouping such strips together, it can be seen that for
$a_{2i,j+1} \cap \Sigma _g^\circ$
. Grouping such strips together, it can be seen that for
![]() $1\le i \le (d-3)/2$
, the
$1\le i \le (d-3)/2$
, the
![]() $2i^{th}$
row of the Lönne graph gives rise to
$2i^{th}$
row of the Lönne graph gives rise to
![]() $d$
strips. In the last row, there are
$d$
strips. In the last row, there are
![]() $d-1$
strips. So in total there are
$d-1$
strips. So in total there are
![]() $1/2(d+1)(d-2)$
strips, and each strip contributes
$1/2(d+1)(d-2)$
strips, and each strip contributes
![]() $-1$
to the Euler characteristic.
$-1$
to the Euler characteristic.
Recall the relation
![]() $g = (d-1)(d-2)/2$
: this means that
$g = (d-1)(d-2)/2$
: this means that
Each
![]() $A_i$
has Euler characteristic
$A_i$
has Euler characteristic
![]() $\chi (A_i) = 2-d$
. It follows that
$\chi (A_i) = 2-d$
. It follows that
 \begin{align*} \chi (\Sigma _g^\circ ) = \chi (\Sigma _g) - \sum _{i = 1}^{(d-1)/2} \chi (A_i) &= 2 - (d-1)(d-2) + (d-1)(d-2)/2\\ &= 2 - (d-1)(d-2)/2. \end{align*}
\begin{align*} \chi (\Sigma _g^\circ ) = \chi (\Sigma _g) - \sum _{i = 1}^{(d-1)/2} \chi (A_i) &= 2 - (d-1)(d-2) + (d-1)(d-2)/2\\ &= 2 - (d-1)(d-2)/2. \end{align*}
Therefore,
We claim that
![]() $\Sigma _g^{\circ \circ }$
has
$\Sigma _g^{\circ \circ }$
has
![]() $d$
boundary components. This will finish the proof, as a surface of Euler characteristic
$d$
boundary components. This will finish the proof, as a surface of Euler characteristic
![]() $d$
and
$d$
and
![]() $b = d$
boundary components must be a union of
$b = d$
boundary components must be a union of
![]() $d$
disks. The claim can easily be checked directly in the case
$d$
disks. The claim can easily be checked directly in the case
![]() $d = 5$
of immediate relevance. For general
$d = 5$
of immediate relevance. For general
![]() $d$
, this follows from a straightforward, if notationally tedious, verification, proceeding by an analysis of the cyclic ordering of the arcs
$d$
, this follows from a straightforward, if notationally tedious, verification, proceeding by an analysis of the cyclic ordering of the arcs
![]() $a_{i,j}$
around the boundary components
$a_{i,j}$
around the boundary components
![]() $\partial A_k^+$
.
$\partial A_k^+$
.
Step 2: A convenient configuration

Figure 9. A Lönne configuration on
![]() $\Sigma _6$
. Only a portion of the figure has been drawn: the omitted curves are obtained by applying the involution
$\Sigma _6$
. Only a portion of the figure has been drawn: the omitted curves are obtained by applying the involution
![]() $\iota$
to the depicted curves.
$\iota$
to the depicted curves.
Figure 9 presents a picture of a Lönne configuration in the case of interest
![]() $d = 5$
. This was obtained by “building the surface” curve by curve, attaching one-handles in the sequence indicated by the numbering of the curves
$d = 5$
. This was obtained by “building the surface” curve by curve, attaching one-handles in the sequence indicated by the numbering of the curves
![]() $a_1, \dots, a_{16}$
. There are other, more uniform depictions of Lönne configurations which arise from Akbulut–Kirby’s picture of a plane curve of degree
$a_1, \dots, a_{16}$
. There are other, more uniform depictions of Lönne configurations which arise from Akbulut–Kirby’s picture of a plane curve of degree
![]() $d$
derived from a Seifert surface of the
$d$
derived from a Seifert surface of the
![]() $(d,d)$
torus link (see [Reference Akbulut and Kirby2] or [ [Reference Gompf and Stipsicz14], Section 6.2.7]), but the analysis to follow is easier to carry out using the model of Figure 9.
$(d,d)$
torus link (see [Reference Akbulut and Kirby2] or [ [Reference Gompf and Stipsicz14], Section 6.2.7]), but the analysis to follow is easier to carry out using the model of Figure 9.
Step 3: Producing vanishing cycles
The bulk of this step will establish claim (1); claim (2) follows as an immediate porism. The set of vanishing cycles is invariant under the action of the monodromy group, since acting by a monodromy element on a nodal degeneration amounts to changing the path along which the nodal degeneration is performed. In particular, if
![]() $a$
and
$a$
and
![]() $b$
are vanishing cycles, then so is
$b$
are vanishing cycles, then so is
![]() $T_a(b)$
. To begin with, curves
$T_a(b)$
. To begin with, curves
![]() $c_1,c_2, c_4, c_8,$
and
$c_1,c_2, c_4, c_8,$
and
![]() $c_{12}$
are elements of the Lönne configuration and so are already vanishing cycles. The curve
$c_{12}$
are elements of the Lönne configuration and so are already vanishing cycles. The curve
![]() $c_3$
is obtained as
$c_3$
is obtained as
similarly,
Curve
![]() $c_{10}$
is obtained as
$c_{10}$
is obtained as
![]() $c_6$
is obtained from
$c_6$
is obtained from
![]() $a_{14}$
and
$a_{14}$
and
![]() $a_{16}$
analogously.
$a_{16}$
analogously.
The curve
![]() $c_9$
is obtained as
$c_9$
is obtained as
![]() $c_7$
is obtained from
$c_7$
is obtained from
![]() $a_{10}, a_{12},$
and
$a_{10}, a_{12},$
and
![]() $c_6$
analogously.
$c_6$
analogously.
To obtain
![]() $c_5$
, twist
$c_5$
, twist
![]() $a_{13}$
along the chain
$a_{13}$
along the chain
![]() $c_6, \dots, c_{10}$
:
$c_6, \dots, c_{10}$
:
![]() $c_{11}$
is obtained by an analogous procedure on
$c_{11}$
is obtained by an analogous procedure on
![]() $a_{14}$
.
$a_{14}$
.
The sequence of twists used to exhibit
![]() $x$
as a vanishing cycle is illustrated in Figure 10. Symbolically,
$x$
as a vanishing cycle is illustrated in Figure 10. Symbolically,
![]() $y$
is produced in an analogous fashion, starting with
$y$
is produced in an analogous fashion, starting with
![]() $a_{8}$
in place of
$a_{8}$
in place of
![]() $a_6$
.
$a_6$
.
To produce
![]() $z$
, we appeal to the genus-
$z$
, we appeal to the genus-
![]() $2$
star relation. Applied to the surface bounded by
$2$
star relation. Applied to the surface bounded by
![]() $b,y,z$
, it shows that
$b,y,z$
, it shows that
![]() $T_b^2 T_y T_z \in \mathrm{Im}(\rho _5)$
, and hence
$T_b^2 T_y T_z \in \mathrm{Im}(\rho _5)$
, and hence
![]() $T_{b}^2 T_z \in \mathrm{Im}(\rho _5)$
since
$T_{b}^2 T_z \in \mathrm{Im}(\rho _5)$
since
![]() $T_y \in \mathrm{Im}(\rho _5)$
by above. Observe that
$T_y \in \mathrm{Im}(\rho _5)$
by above. Observe that
![]() $i(c_{10}, z) = 1$
, and that
$i(c_{10}, z) = 1$
, and that
![]() $T_{c_{10}} \in \mathrm{Im}(\rho _5)$
. Making use of the fact that
$T_{c_{10}} \in \mathrm{Im}(\rho _5)$
. Making use of the fact that
![]() $b$
is disjoint from both
$b$
is disjoint from both
![]() $z$
and
$z$
and
![]() $c_{10}$
, the braid relation gives
$c_{10}$
, the braid relation gives
This exhibits
![]() $z$
as a vanishing cycle, establishing claim (1) of Lemma 6.1. As
$z$
as a vanishing cycle, establishing claim (1) of Lemma 6.1. As
![]() $T_b^2 T_z$
and
$T_b^2 T_z$
and
![]() $T_z$
are now both known to be elements of
$T_z$
are now both known to be elements of
![]() $\mathrm{Im}(\rho _5)$
, it follows that
$\mathrm{Im}(\rho _5)$
, it follows that
![]() $T_b^2 \in \mathrm{Im}(\rho _5)$
as well, completing claim (2).
$T_b^2 \in \mathrm{Im}(\rho _5)$
as well, completing claim (2).

Figure 10. The sequence of twists used to obtain
![]() $x$
.
$x$
.
7. Proof of Theorem 1.2
In this final section, we assemble the work we have done so far in order to prove Theorem 1.2.
7.1. Step 1: Reduction to the Torelli group
The first step is to reduce the problem of determining
![]() $\mathrm{Im}(\rho _5)$
to the determination of
$\mathrm{Im}(\rho _5)$
to the determination of
![]() $\mathrm{Im}(\rho _5) \cap \mathcal{I}_6$
. This will follow from [Reference Beauville4]. Recall that Beauville establishes that
$\mathrm{Im}(\rho _5) \cap \mathcal{I}_6$
. This will follow from [Reference Beauville4]. Recall that Beauville establishes that
![]() $\mathrm{Im}(\Psi \circ \rho _5)$
is the entire stabilizer of an odd-parity spin structure on
$\mathrm{Im}(\Psi \circ \rho _5)$
is the entire stabilizer of an odd-parity spin structure on
![]() $H_1(\Sigma _6;{\mathbb{Z}})$
. This spin structure was identified as
$H_1(\Sigma _6;{\mathbb{Z}})$
. This spin structure was identified as
![]() $\phi _5$
in Section 2. Therefore,
$\phi _5$
in Section 2. Therefore,
![]() $\mathrm{Im}(\Psi \circ \rho _5) = \mathrm{Im}(\Psi \circ \operatorname{Mod}(\Sigma _6)[\phi _5])$
. It, therefore, suffices to show that
$\mathrm{Im}(\Psi \circ \rho _5) = \mathrm{Im}(\Psi \circ \operatorname{Mod}(\Sigma _6)[\phi _5])$
. It, therefore, suffices to show that

Figure 11. The cases of step 2.
7.2. Step 2: Enumeration of cases
Equation (7) will be derived as a consequence of Theorem4.6. Lemma 6.1.1 asserts that the curves
![]() $c_1, \dots, c_{12}$
in the Johnson generating set are contained in
$c_1, \dots, c_{12}$
in the Johnson generating set are contained in
![]() $\mathrm{Im}(\rho _5)$
, so that the first hypothesis of Theorem4.6 is satisfied. There are then eight cases to check: the four straight chain maps of the form
$\mathrm{Im}(\rho _5)$
, so that the first hypothesis of Theorem4.6 is satisfied. There are then eight cases to check: the four straight chain maps of the form
![]() $(c_1, \dots, c_k)$
for
$(c_1, \dots, c_k)$
for
![]() $k = 3,5,7,9$
and the four
$k = 3,5,7,9$
and the four
![]() $\beta$
-chain maps of the form
$\beta$
-chain maps of the form
![]() $(\beta, c_5, \dots, c_k)$
for
$(\beta, c_5, \dots, c_k)$
for
![]() $k = 6, 8, 10, 12$
. See Figure 11.
$k = 6, 8, 10, 12$
. See Figure 11.
The verification of the
![]() $\beta$
-chain cases will be easier to accomplish after conjugating by the class
$\beta$
-chain cases will be easier to accomplish after conjugating by the class
![]() $g = T_x T_{c_5}^{-1} T_{c_4}^{-1} \in \mathrm{Im}(\rho _5)$
. This has the following effect on the curves in the
$g = T_x T_{c_5}^{-1} T_{c_4}^{-1} \in \mathrm{Im}(\rho _5)$
. This has the following effect on the curves in the
![]() $\beta$
-chains (the curve
$\beta$
-chains (the curve
![]() $\gamma$
is indicated in Figure 11 in the picture for
$\gamma$
is indicated in Figure 11 in the picture for
![]() $k = 6$
):
$k = 6$
):
7.3. Step 3: Producing bounding-pair maps
In this step, we explain the method by which we will obtain the necessary bounding-pair maps. This is an easy consequence of the chain relation.
Lemma 7.1.
Let
![]() $C = (c_1, \dots, c_k)$
be a chain of odd length
$C = (c_1, \dots, c_k)$
be a chain of odd length
![]() $k$
and boundary
$k$
and boundary
![]() $\partial C = d_1 \cup d_2$
. Suppose that the mapping classes
$\partial C = d_1 \cup d_2$
. Suppose that the mapping classes
are all contained in some subgroup
![]() $\Gamma \le \textrm{Mod}(\Sigma _g)$
. Then the chain map associated to
$\Gamma \le \textrm{Mod}(\Sigma _g)$
. Then the chain map associated to
![]() $C$
(i.e., the bounding pair map
$C$
(i.e., the bounding pair map
![]() $T_{d_1} T_{d_2}^{-1}$
) is also contained in
$T_{d_1} T_{d_2}^{-1}$
) is also contained in
![]() $\Gamma$
.
$\Gamma$
.
Proof. The chain relation (Proposition 4.4) implies that
![]() $T_{d_1} T_{d_2} \in \Gamma$
. By hypothesis,
$T_{d_1} T_{d_2} \in \Gamma$
. By hypothesis,
![]() $T_{d_1}^2 \in \Gamma$
, so the bounding pair map
$T_{d_1}^2 \in \Gamma$
, so the bounding pair map
![]() $T_{d_1}T_{d_2}^{-1} \in \Gamma$
as well.
$T_{d_1}T_{d_2}^{-1} \in \Gamma$
as well.
7.4. Step 4: Verification of cases
Lemma 6.1 asserts that the classes
![]() $T_{c_i}, 1 \le i \le 12$
, as well as
$T_{c_i}, 1 \le i \le 12$
, as well as
![]() $T_b^2$
are all contained in
$T_b^2$
are all contained in
![]() $\mathrm{Im}(\rho _5)$
. The class
$\mathrm{Im}(\rho _5)$
. The class
![]() $\gamma$
is obtained from
$\gamma$
is obtained from
![]() $c_6$
by the element
$c_6$
by the element
![]() $g \in \mathrm{Im}(\rho _5)$
, so
$g \in \mathrm{Im}(\rho _5)$
, so
![]() $\gamma$
is a vanishing cycle as well. Via Lemma 7.1, it remains only to show that in each of the cases in Step 2, one of the boundary components
$\gamma$
is a vanishing cycle as well. Via Lemma 7.1, it remains only to show that in each of the cases in Step 2, one of the boundary components
![]() $d_1$
satisfies
$d_1$
satisfies
![]() $T_{d_1}^2 \in \mathrm{Im}(\rho _5)$
.
$T_{d_1}^2 \in \mathrm{Im}(\rho _5)$
.
The straight chain maps are depicted in the left-hand column of Figure 11. For
![]() $k = 3$
, one boundary component is
$k = 3$
, one boundary component is
![]() $b$
; we have already remarked how
$b$
; we have already remarked how
![]() $T_b^2 \in \mathrm{Im}(\rho _5)$
. For
$T_b^2 \in \mathrm{Im}(\rho _5)$
. For
![]() $k = 5$
, one of the boundary components is
$k = 5$
, one of the boundary components is
![]() $x$
. For
$x$
. For
![]() $k = 7$
, one uses the methods of Lemma 6.1 to show that the right-hand boundary component
$k = 7$
, one uses the methods of Lemma 6.1 to show that the right-hand boundary component
![]() $c$
satisfies
$c$
satisfies
![]() $T_c^2 \in \mathrm{Im}(\rho _5)$
(the proof is identical to that for
$T_c^2 \in \mathrm{Im}(\rho _5)$
(the proof is identical to that for
![]() $b$
). Finally, for
$b$
). Finally, for
![]() $k = 9$
, one of the boundary components is
$k = 9$
, one of the boundary components is
![]() $y$
.
$y$
.
We turn to the
![]() $\beta$
-chains. The images of the
$\beta$
-chains. The images of the
![]() $\beta$
-chains under the map
$\beta$
-chains under the map
![]() $g$
are depicted in the right-hand column of Figure 11. For
$g$
are depicted in the right-hand column of Figure 11. For
![]() $k = 6,8,10,12$
, let
$k = 6,8,10,12$
, let
![]() $d_k$
denote the boundary component depicted there for the chain
$d_k$
denote the boundary component depicted there for the chain
![]() $(b, c_4, \gamma, c_7, \dots, c_k)$
. Observe that
$(b, c_4, \gamma, c_7, \dots, c_k)$
. Observe that
![]() $d_k$
is also a boundary component of the chain map for
$d_k$
is also a boundary component of the chain map for
![]() $(c_6, \dots, c_k)$
(in the case
$(c_6, \dots, c_k)$
(in the case
![]() $k=6$
, the boundary component
$k=6$
, the boundary component
![]() $d_6$
is just
$d_6$
is just
![]() $c_6$
). Moreover, the chain map for
$c_6$
). Moreover, the chain map for
![]() $(c_6, \dots, c_k)$
is conjugate to the chain map for
$(c_6, \dots, c_k)$
is conjugate to the chain map for
![]() $(c_1, \dots, c_{k-5})$
by an element of
$(c_1, \dots, c_{k-5})$
by an element of
![]() $\mathrm{Im}(\rho _5)$
(this is easy to see using the isomorphism between the group generated by
$\mathrm{Im}(\rho _5)$
(this is easy to see using the isomorphism between the group generated by
![]() $c_1, \dots, c_{12}$
and the braid group
$c_1, \dots, c_{12}$
and the braid group
![]() $B_{13}$
on
$B_{13}$
on
![]() $13$
strands). Via the verification of the straight-chain cases, it follows that
$13$
strands). Via the verification of the straight-chain cases, it follows that
![]() $T_{d_k}^2 \in \mathrm{Im}(\rho _5)$
, and so by Lemma 7.1, the
$T_{d_k}^2 \in \mathrm{Im}(\rho _5)$
, and so by Lemma 7.1, the
![]() $\beta$
-chain maps are also contained in
$\beta$
-chain maps are also contained in
![]() $\mathrm{Im}(\rho _5)$
.
$\mathrm{Im}(\rho _5)$
.
Acknowledgments
The author would like to thank Dan Margalit for a series of valuable discussions concerning this work. He would also like to thank Benson Farb for alerting him to Lönne’s work and for extensive comments on drafts of this paper, as well as ongoing support in his role as advisor. He is also indebted to several anonymous referees whose comments have improved the paper.
Competing interests declaration
The author declares no competing interests.