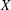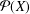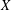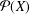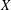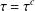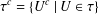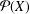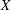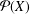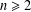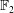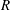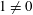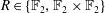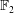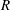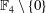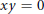Refine search
Actions for selected content:
4 results
FROM TOPOLOGIES OF A SET TO SUBRINGS OF ITS POWER SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 15-20
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Spectra of Boolean Graphs Over Finite Fields of Characteristic Two
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 58-65
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
The Metric Dimension of the Total Graph of a Finite Commutative Ring
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 748-759
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
Characterizations of Three Classes of Zero-Divisor Graphs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 127-137
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation