Refine search
Actions for selected content:
11 results
An analogue of the Milnor conjecture for the de Rham-Witt complex in characteristic 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bökstedt periodicity and quotients of DVRs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 27 September 2022, pp. 1683-1712
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Witt vectors with coefficients and characteristic polynomials over non-commutative rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 366-408
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
De Rham–Witt sheaves via algebraic cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 2089-2132
- Print publication:
- October 2021
-
- Article
- Export citation
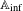 $\mathbb{A}_{\text{inf}}$ IS INFINITE DIMENSIONAL
$\mathbb{A}_{\text{inf}}$ IS INFINITE DIMENSIONAL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 11 May 2020, pp. 1983-1989
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
BREUIL–KISIN–FARGUES MODULES WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 21 January 2020, pp. 1855-1904
- Print publication:
- November 2021
-
- Article
- Export citation
CANONICAL LIFTS OF FAMILIES OFELLIPTIC CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 02 November 2017, pp. 193-213
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
Zero cycles with modulus and zero cycles on singular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 120-187
- Print publication:
- January 2018
-
- Article
- Export citation
ON THE WEAK GROTHENDIECK GROUP OF A BEZOUT RING
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 617-635
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
L-functions of p-adic characters
-
- Journal:
- Nagoya Mathematical Journal / Volume 213 / March 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 77-104
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Nonarchimedean geometry of Witt vectors
-
- Journal:
- Nagoya Mathematical Journal / Volume 209 / March 2013
- Published online by Cambridge University Press:
- 11 January 2016, pp. 111-165
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
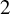
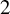
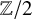
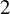
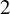
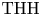
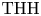
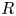
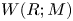
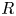
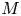
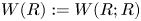
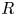
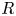
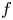
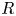
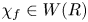
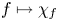
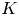
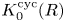
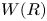
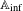
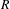
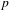
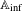
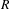
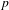
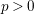
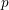
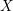
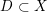
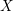
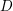
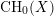
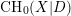
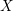
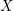
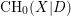
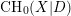
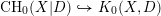
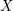
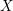
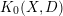
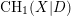
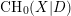
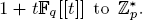 For
For  to exhibit a bijection between
to exhibit a bijection between  indexed by natural numbers relatively prime to
indexed by natural numbers relatively prime to 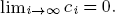 . To such a
. To such a 