Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-12T00:51:42.287Z Has data issue: false hasContentIssue false
  • English
  • Français

L-functions of p-adic characters

Published online by Cambridge University Press:  11 January 2016

Christopher Davis  and
Daqing Wan
Christopher Davis*
Affiliation:
Department of Mathematics University of California, Irvine, Irvine, California 92697, USA
Daqing Wan
Affiliation:
Department of Mathematics University of California, Irvine, Irvine, California 92697, USA, dwan@math.uci.edu
*
University of Copenhagen Department of Mathematical Sciences, Universitetsparken 5 2100 København Ø, Denmark, davis@math.ku.dk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define a p-adic character to be a continuous homomorphism from 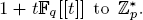For p > 2, we use the ring of big Witt vectors over 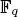to exhibit a bijection between p-adic characters and sequences (ci)(i,p)=1 of elements in indexed by natural numbers relatively prime to p, and for which 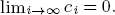. To such a p-adic character we associate an L-function, and we prove that this L-function is p-adic meromorphic if the corresponding sequence (ci) is overconvergent. If more generally the sequence is C log-convergent, we show that the associated L-function is meromorphic in the open disk of radius qC. Finally, we exhibit examples of C log-convergent sequences with associated L-functions which are not meromorphic in the disk of radius qC+∊ for any ∊ > 0.

Keywords

11G4013F35
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 213 , March 2014 , pp. 77 - 104
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2014

References

[1] Bourbaki, N., Éléments de mathématique: Algèbre commutative, chapitres 8 et 9, reprint of the 1983 original, Springer, Berlin, 2006. MR 2284892.Google Scholar
[2] Coleman, R. F., p-adic Banach spaces and families of modular forms, Invent. Math. 127 (1997), 417–479. MR 1431135. DOI 10.1007/s002220050127.CrossRefGoogle Scholar
[3] Coleman, R. and Mazur, B., “The eigencurve” in Galois Representations in Arithmetic Algebraic Geometry (Durham, England, 1996), London Math. Soc. Lecture Note Ser. 254, Cambridge University Press, Cambridge, 1998, 1–113. MR 1696469. DOI 10. 1017/CBO9780511662010.003.Google Scholar
[4] Crew, R., L-functions of p-adic characters and geometric Iwasawa theory, Invent. Math. 88 (1987), 395-403. MR 0880957. DOI 10.1007/BF01388914.CrossRefGoogle Scholar
[5] Dwork, B., Normalized period matrices, I: Plane curves, Ann. of Math. (2) 94 (1971), 337–388. MR 0396579.CrossRefGoogle Scholar
[6] Dwork, B., Normalized period matrices, II, Ann. of Math. (2) 98 (1973), 1-57. MR 0396580.CrossRefGoogle Scholar
[7] Emerton, M. and Kisin, M., Unit L-functions and a conjecture of Katz, Ann. of Math. (2) 153 (2001), 329-354. MR 1829753. DOI 10.2307/2661344.CrossRefGoogle Scholar
[8] Hazewinkel, M., Formal Groups and Applications, Pure Appl. Math. 78, Academic Press, New York, 1978. MR 0506881.Google Scholar
[9] Hesselholt, L., The big de Rham-Witt complex, preprint, http://www.math.nagoya-u.ac.jp/~larsh/papers/028/ (accessed 27 August 2013 ).Google Scholar
[10] Katz, N., “Travaux de Dwork” in Séminaire Bourbaki, 24ème année (1971/1972), Exp. No. 409, Lecture Notes in Math. 317, Springer, Berlin, 1973, 167-200. MR 0498577.Google Scholar
[11] Kedlaya, K. S., Pottharst, J., and Xiao, L., Cohomology of arithmetic families of (φ,Γ)- modules, preprint, arXiv:1203.5718 [math.NT].CrossRefGoogle Scholar
[12] Koblitz, N., p-Adic Numbers, p-Adic Analysis, and zeta-Functions, 2nd ed., Grad. Texts in Math. 58, Springer, New York, 1984. MR 0754003. DOI 10.1007/ 978-1-4612-1112-9.Google Scholar
[13] Lenstra, H., Construction of the ring of Witt vectors, preprint, http://www.math. leidenuniv.nl/~hwl (accessed 27 August 2013 ).Google Scholar
[14] Liu, C. and Wan, D., T-adic exponential sums over finite fields, Algebra Number Theory 3 (2009), 489-509. MR 2578886. DOI 10.2140/ant.2009.3.489.CrossRefGoogle Scholar
[15] Rabinoff, J., The theory of Witt vectors, preprint, http://www.math.harvard.edu/~rabinoff/misc/witt.pdf (accessed 27 August 2013 ).Google Scholar
[16] Serre, J.-P., Local Fields, Grad. Texts in Math. 67, Springer, New York, 1979. MR 0554237.Google Scholar
[17] Wan, D., Meromorphic continuation of L-functions of p-adic representations, Ann. of Math. (2) 143 (1996), 469–498. MR 1394966. DOI 10.2307/2118533.CrossRefGoogle Scholar
[18] Wan, D., Dwork’s conjecture on unit root zeta functions, Ann. of Math. (2) 150 (1999), 867–927. MR 1740990. DOI 10.2307/121058.CrossRefGoogle Scholar
[19] Wan, D., Higher rank case of Dwork’s conjecture, J. Amer. Math. Soc. 13 (2000), 807–852. MR 1775738. DOI 10.1090/S0894-0347-00-00339-8.CrossRefGoogle Scholar
[20] Wan, D., Rank one case of Dwork’s conjecture, J. Amer. Math. Soc. 13 (2000), 853–908. MR 1775761. DOI 10.1090/S0894-0347-00-00340-4.CrossRefGoogle Scholar
[21] Wan, D., Variation of p-adic Newton polygons for L-functions of exponential sums, Asian J. Math. 8 (2004), 427–471. MR 2129244.Google Scholar