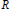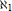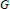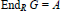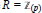Refine search
Actions for selected content:
14 results
Free summands of stably free modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 May 2025, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projective freeness and stable rank of algebras of complex-valued BV functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 844-853
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A FREENESS CRITERION WITHOUT PATCHING FOR MODULES OVER LOCAL RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 2117-2129
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Benson's cofibrants, Gorenstein projectives and a related conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 23 September 2021, pp. 779-799
-
- Article
- Export citation
A Module-theoretic Characterization of Algebraic Hypersurfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 166-173
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
Proof of de Smit’s conjecture: a freeness criterion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 2310-2317
- Print publication:
- November 2017
-
- Article
- Export citation
Quillen's solution of Serre's Problem
-
- Journal:
- Journal of K-Theory / Volume 11 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 11 March 2013, pp. 549-552
- Print publication:
- June 2013
-
- Article
- Export citation
DECOMPOSITION OF JORDAN AUTOMORPHISMS OF TRIANGULAR MATRIX ALGEBRA OVER COMMUTATIVE RINGS
-
- Journal:
- Glasgow Mathematical Journal / Volume 52 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 25 August 2010, pp. 529-536
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Acyclicity of Complexes of Flat Modules
-
- Journal:
- Nagoya Mathematical Journal / Volume 192 / 2008
- Published online by Cambridge University Press:
- 11 January 2016, pp. 111-118
- Print publication:
- 2008
-
- Article
-
- You have access
- Export citation
THE UNIT SUM NUMBER OF SOME PROJECTIVE MODULES
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 71-74
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
Indecomposable Almost Free Modules—The Local Case
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 4 / 01 August 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 719-738
- Print publication:
- 01 August 1998
-
- Article
-
- You have access
- Export citation
A Problem on Relative Projectivity for Abelian Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 1 / 01 March 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 114-122
- Print publication:
- 01 March 1986
-
- Article
-
- You have access
- Export citation
Free Summands of Stably Free Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 3 / 01 September 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 361-362
- Print publication:
- 01 September 1982
-
- Article
-
- You have access
- Export citation
On the Smoothness of Generic Rings for Stably Free Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 1 / 01 March 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 64-70
- Print publication:
- 01 March 1982
-
- Article
-
- You have access
- Export citation













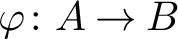
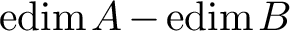
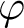
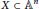

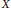
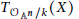
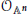

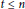
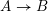
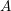
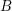
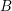
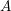
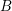
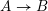
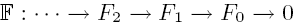
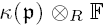 is acyclic for every ρ ϵ Spec
is acyclic for every ρ ϵ Spec 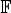 is acyclic, and H
is acyclic, and H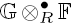 is exact for every
is exact for every 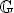 . If, moreover,
. If, moreover, 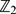 is not a factor of
is not a factor of