Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hashimoto, Mitsuyasu
2015.
Equivariant Total Ring of Fractions and Factoriality of Rings Generated by Semi-Invariants.
Communications in Algebra,
Vol. 43,
Issue. 4,
p.
1524.

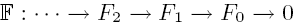
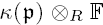 is acyclic for every ρ ϵ Spec
is acyclic for every ρ ϵ Spec 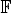 is acyclic, and H
is acyclic, and H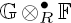 is exact for every
is exact for every 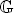 . If, moreover,
. If, moreover, 