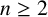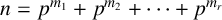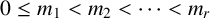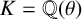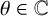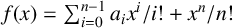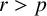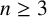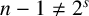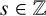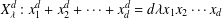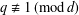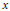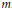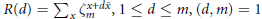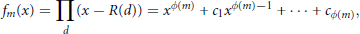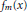Refine search
Actions for selected content:
12 results
NONMONOGENITY OF NUMBER FIELDS DEFINED BY TRUNCATED EXPONENTIAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 497-504
- Print publication:
- June 2025
-
- Article
- Export citation
A CONJECTURE OF ZHI-WEI SUN ON MATRICES CONCERNING MULTIPLICATIVE SUBGROUPS OF FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 490-496
- Print publication:
- June 2025
-
- Article
- Export citation
GENERATORS OF FINITE FIELDS WITH PRESCRIBED TRACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 355-366
- Print publication:
- June 2022
-
- Article
- Export citation
THE HOLOMORPHY CONJECTURE FOR NONDEGENERATE SURFACE SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 28 October 2016, pp. 160-188
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
COUNTING POINTS ON DWORK HYPERSURFACES AND
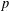 $p$ -ADIC HYPERGEOMETRIC FUNCTIONS
$p$ -ADIC HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 208-216
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Character Sums Over Bohr Sets
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 4 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 774-786
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Harmonic Analysis Related to Homogeneous Varieties in Three Dimensional Vector Spaces over Finite Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 5 / 01 October 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1036-1057
- Print publication:
- 01 October 2012
-
- Article
-
- You have access
- Export citation
NOTE ON A PAPER OF J. HOFFSTEIN
-
- Journal:
- Glasgow Mathematical Journal / Volume 49 / Issue 2 / May 2007
- Published online by Cambridge University Press:
- 09 August 2007, pp. 243-255
- Print publication:
- May 2007
-
- Article
-
- You have access
- Export citation
Polynomials for Kloosterman Sums
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 1 / 01 March 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 71-84
- Print publication:
- 01 March 2007
-
- Article
-
- You have access
- Export citation
PRIMITIVE POLYNOMIALS WITH PRESCRIBED SECOND COEFFICIENT
-
- Journal:
- Glasgow Mathematical Journal / Volume 48 / Issue 2 / May 2006
- Published online by Cambridge University Press:
- 23 August 2006, pp. 281-307
- Print publication:
- May 2006
-
- Article
-
- You have access
- Export citation
Gauss and Eisenstein Sums of Order Twelve
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 3 / 01 September 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-355
- Print publication:
- 01 September 2003
-
- Article
-
- You have access
- Export citation
Gauss Sums of Orders Six and Twelve
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 1 / 01 March 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 22-26
- Print publication:
- 01 March 2001
-
- Article
-
- You have access
- Export citation