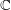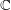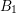1 Introduction
Let
![]() $K$
be a finite extension of the field of
$K$
be a finite extension of the field of
![]() $p$
-adic numbers
$p$
-adic numbers
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
![]() $R$
be the valuation ring of
$R$
be the valuation ring of
![]() $K$
, and let
$K$
, and let
![]() $P$
be its maximal ideal. Suppose that the residue field
$P$
be its maximal ideal. Suppose that the residue field
![]() $R/P$
has cardinality
$R/P$
has cardinality
![]() $q$
. For
$q$
. For
![]() $z\in K$
, let
$z\in K$
, let
![]() $\text{ord}(z)\in \mathbb{Z}\cup \left\{\infty \right\}$
denote its valuation, let
$\text{ord}(z)\in \mathbb{Z}\cup \left\{\infty \right\}$
denote its valuation, let
![]() $|z|=q^{-\text{ord}(z)}$
be its absolute value, and let
$|z|=q^{-\text{ord}(z)}$
be its absolute value, and let
![]() $ac(z)=z\unicode[STIX]{x1D70B}^{-\text{ord}(z)}$
be its angular component, where
$ac(z)=z\unicode[STIX]{x1D70B}^{-\text{ord}(z)}$
be its angular component, where
![]() $\unicode[STIX]{x1D70B}$
is a fixed uniformizing parameter for
$\unicode[STIX]{x1D70B}$
is a fixed uniformizing parameter for
![]() $R$
.
$R$
.
Let
![]() $f(\text{}\underline{x})$
,
$f(\text{}\underline{x})$
,
![]() $\text{}\underline{x}:=(x_{1},\ldots ,x_{n})$
, be a nonconstant polynomial over
$\text{}\underline{x}:=(x_{1},\ldots ,x_{n})$
, be a nonconstant polynomial over
![]() $K$
, and let
$K$
, and let
![]() $\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
be a multiplicative character of
$\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
be a multiplicative character of
![]() $R^{\times }$
; that is, a homomorphism with finite image. We formally put
$R^{\times }$
; that is, a homomorphism with finite image. We formally put
![]() $\unicode[STIX]{x1D712}(0)=0$
. Let
$\unicode[STIX]{x1D712}(0)=0$
. Let
![]() $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
, respectively
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
, respectively
![]() $Z_{f}(\unicode[STIX]{x1D712},K,s)$
, be the corresponding local Igusa zeta function, respectively global Igusa zeta function; that is, the meromorphic continuation to
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
, be the corresponding local Igusa zeta function, respectively global Igusa zeta function; that is, the meromorphic continuation to
![]() $\mathbb{C}$
of the integral function
$\mathbb{C}$
of the integral function
 $$\begin{eqnarray}\displaystyle & \displaystyle Z_{0}(s)=\int _{P^{n}}\unicode[STIX]{x1D712}\left(ac(f(\text{}\underline{x}))\right)|f(\text{}\underline{x})|^{s}|d(\text{}\underline{x})|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{respectively }Z(s)=\int _{R^{n}}\unicode[STIX]{x1D712}\left(ac(f(\text{}\underline{x}))\right)|f(\text{}\underline{x})|^{s}|d(\text{}\underline{x})|, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Z_{0}(s)=\int _{P^{n}}\unicode[STIX]{x1D712}\left(ac(f(\text{}\underline{x}))\right)|f(\text{}\underline{x})|^{s}|d(\text{}\underline{x})|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{respectively }Z(s)=\int _{R^{n}}\unicode[STIX]{x1D712}\left(ac(f(\text{}\underline{x}))\right)|f(\text{}\underline{x})|^{s}|d(\text{}\underline{x})|, & \displaystyle \nonumber\end{eqnarray}$$
for
![]() $s\in \mathbb{C}$
, with
$s\in \mathbb{C}$
, with
![]() $Re(s)>0$
, where
$Re(s)>0$
, where
![]() $|d(\text{}\underline{x})|=|dx_{1}\wedge \cdots \wedge dx_{n}|$
denotes the Haar measure on
$|d(\text{}\underline{x})|=|dx_{1}\wedge \cdots \wedge dx_{n}|$
denotes the Haar measure on
![]() $K^{n}$
normalized such that the measure of
$K^{n}$
normalized such that the measure of
![]() $R^{n}$
is
$R^{n}$
is
![]() $1$
.
$1$
.
For
![]() $f$
a polynomial over
$f$
a polynomial over
![]() $R$
, the local and global Igusa zeta function can be described in terms of solutions of congruences. For
$R$
, the local and global Igusa zeta function can be described in terms of solutions of congruences. For
![]() $i\in \mathbb{N}_{{>}0}$
and
$i\in \mathbb{N}_{{>}0}$
and
![]() $u\in R/P^{i}$
, let
$u\in R/P^{i}$
, let
![]() $M_{0,i}(u)$
and
$M_{0,i}(u)$
and
![]() $M_{i}(u)$
be the number of solutions of
$M_{i}(u)$
be the number of solutions of
![]() $f(\text{}\underline{x})\equiv u\text{ mod }P^{i}$
in
$f(\text{}\underline{x})\equiv u\text{ mod }P^{i}$
in
![]() $(P/P^{i})^{n}$
and
$(P/P^{i})^{n}$
and
![]() $(R/P^{i})^{n}$
respectively. Let
$(R/P^{i})^{n}$
respectively. Let
![]() $c$
be the conductor of
$c$
be the conductor of
![]() $\unicode[STIX]{x1D712}$
; that is, the smallest
$\unicode[STIX]{x1D712}$
; that is, the smallest
![]() $a\in \mathbb{N}_{{>}0}$
such that
$a\in \mathbb{N}_{{>}0}$
such that
![]() $\unicode[STIX]{x1D712}$
is trivial on
$\unicode[STIX]{x1D712}$
is trivial on
![]() $1+P^{a}$
. Then,
$1+P^{a}$
. Then,
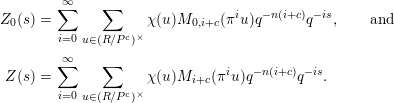 $$\begin{eqnarray}\displaystyle Z_{0}(s) & = & \displaystyle \mathop{\sum }_{i=0}^{\infty }\mathop{\sum }_{u\in (R/P^{c})^{\times }}\unicode[STIX]{x1D712}(u)M_{0,i+c}(\unicode[STIX]{x1D70B}^{i}u)q^{-n(i+c)}q^{-is},\qquad \text{and}\qquad \nonumber\\ \displaystyle Z(s) & = & \displaystyle \mathop{\sum }_{i=0}^{\infty }\mathop{\sum }_{u\in (R/P^{c})^{\times }}\unicode[STIX]{x1D712}(u)M_{i+c}(\unicode[STIX]{x1D70B}^{i}u)q^{-n(i+c)}q^{-is}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{0}(s) & = & \displaystyle \mathop{\sum }_{i=0}^{\infty }\mathop{\sum }_{u\in (R/P^{c})^{\times }}\unicode[STIX]{x1D712}(u)M_{0,i+c}(\unicode[STIX]{x1D70B}^{i}u)q^{-n(i+c)}q^{-is},\qquad \text{and}\qquad \nonumber\\ \displaystyle Z(s) & = & \displaystyle \mathop{\sum }_{i=0}^{\infty }\mathop{\sum }_{u\in (R/P^{c})^{\times }}\unicode[STIX]{x1D712}(u)M_{i+c}(\unicode[STIX]{x1D70B}^{i}u)q^{-n(i+c)}q^{-is}.\nonumber\end{eqnarray}$$
Igusa showed that these functions are rational functions in
![]() $q^{-s}$
, and he gave a formula for
$q^{-s}$
, and he gave a formula for
![]() $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},K,s)$
in terms of an embedded resolution
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
in terms of an embedded resolution
![]() $(Y,h)$
of
$(Y,h)$
of
![]() $f^{-1}\{0\}$
over
$f^{-1}\{0\}$
over
![]() $K$
(see [Reference IgusaI]). Let
$K$
(see [Reference IgusaI]). Let
![]() $E_{j}$
,
$E_{j}$
,
![]() $j\in T$
, be the (reduced) irreducible components of
$j\in T$
, be the (reduced) irreducible components of
![]() $h^{-1}(f^{-1}\left\{0\right\})$
, and let
$h^{-1}(f^{-1}\left\{0\right\})$
, and let
![]() $N_{j}$
, respectively
$N_{j}$
, respectively
![]() $\unicode[STIX]{x1D708}_{j}-1$
, be the multiplicity of
$\unicode[STIX]{x1D708}_{j}-1$
, be the multiplicity of
![]() $E_{j}$
in the divisor of
$E_{j}$
in the divisor of
![]() $f\circ h$
, respectively
$f\circ h$
, respectively
![]() $h^{\ast }(dx_{1}\wedge \cdots \wedge dx_{n})$
on
$h^{\ast }(dx_{1}\wedge \cdots \wedge dx_{n})$
on
![]() $Y$
. Then, the poles of
$Y$
. Then, the poles of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},K,s)$
are among the values
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
are among the values
for which the order of
![]() $\unicode[STIX]{x1D712}$
divides
$\unicode[STIX]{x1D712}$
divides
![]() $N_{j}$
.
$N_{j}$
.
Let now
![]() $f\in F[\text{}\underline{x}]$
, with
$f\in F[\text{}\underline{x}]$
, with
![]() $F\subset \mathbb{C}$
a number field, and let
$F\subset \mathbb{C}$
a number field, and let
![]() $K$
be a nonarchimedean completion of
$K$
be a nonarchimedean completion of
![]() $F$
; that is, a completion with respect to a finite prime. Let
$F$
; that is, a completion with respect to a finite prime. Let
![]() $R$
be its valuation ring, and let
$R$
be its valuation ring, and let
![]() $\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
be a multiplicative character. Then, the poles of
$\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
be a multiplicative character. Then, the poles of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},K,s)$
seem to be related to various invariants in singularity theory, such as the eigenvalues of monodromy and the roots of the Bernstein–Sato polynomial (see, for example, [Reference DenefD2]) and such as the jumping numbers (see, for example, [Reference Smith and ThompsonST]). In this article, we explore another connection conjectured by Denef, called the holomorphy conjecture. It follows from (1) that when the order of
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
seem to be related to various invariants in singularity theory, such as the eigenvalues of monodromy and the roots of the Bernstein–Sato polynomial (see, for example, [Reference DenefD2]) and such as the jumping numbers (see, for example, [Reference Smith and ThompsonST]). In this article, we explore another connection conjectured by Denef, called the holomorphy conjecture. It follows from (1) that when the order of
![]() $\unicode[STIX]{x1D712}$
divides no
$\unicode[STIX]{x1D712}$
divides no
![]() $N_{j}$
at all, then the zeta functions
$N_{j}$
at all, then the zeta functions
![]() $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},K,s)$
are holomorphic on
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
are holomorphic on
![]() $\mathbb{C}$
. Now, the
$\mathbb{C}$
. Now, the
![]() $N_{j}$
are not intrinsically associated to
$N_{j}$
are not intrinsically associated to
![]() $f^{-1}\left\{0\right\}$
; however, the order (as root of unity) of any eigenvalue of the local monodromy on
$f^{-1}\left\{0\right\}$
; however, the order (as root of unity) of any eigenvalue of the local monodromy on
![]() $f^{-1}\left\{0\right\}$
divides some
$f^{-1}\left\{0\right\}$
divides some
![]() $N_{j}$
, and those eigenvalues are intrinsic invariants of
$N_{j}$
, and those eigenvalues are intrinsic invariants of
![]() $f^{-1}\left\{0\right\}$
. This observation inspired Denef to propose the following [Reference DenefD2, Conjecture 4.4.2].
$f^{-1}\left\{0\right\}$
. This observation inspired Denef to propose the following [Reference DenefD2, Conjecture 4.4.2].
Conjecture 1. (Holomorphy conjecture)
For almost all nonarchimedean completions
![]() $K$
of
$K$
of
![]() $F$
(i.e., for all except a finite number) and all characters
$F$
(i.e., for all except a finite number) and all characters
![]() $\unicode[STIX]{x1D712}$
, the local (resp. global) Igusa zeta function
$\unicode[STIX]{x1D712}$
, the local (resp. global) Igusa zeta function
![]() $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
(resp.
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
(resp.
![]() $Z_{f}(\unicode[STIX]{x1D712},K,s)$
) is holomorphic, unless the order of
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
) is holomorphic, unless the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of the local monodromy of
$\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of the local monodromy of
![]() $f$
at some complex point of
$f$
at some complex point of
![]() $f^{-1}\left\{0\right\}$
.
$f^{-1}\left\{0\right\}$
.
This conjecture was proved by Veys in [Reference VeysVe, Theorem 3.1] for plane curves, and in [Reference Denef and VeysDV], Denef and Veys obtained a Thom–Sebastiani-type result. In [Reference Rodrigues and VeysRV], Rodrigues and Veys make progress on the holomorphy conjecture for homogeneous polynomials. Veys and Lemahieu confirmed the conjecture for surfaces that are general for a toric idealistic cluster (see [Reference Lemahieu and VeysLV, Theorem 24]). In [Reference Lemahieu and Van ProeyenLVP1], the holomorphy conjecture was introduced for ideals and was proved for ideals in dimension two.
In this article, we prove the holomorphy conjecture for surface singularities that are nondegenerate over
![]() $\mathbb{C}$
with respect to their Newton polyhedron at the origin. In Section 2, we recall this notion, along with explicit formulas for the zeta functions in this context. By a formula of Varchenko, the normalized volume of a face gets a key role in the search for eigenvalues of monodromy for nondegenerate singularities. In Section 3, we prove some properties on the normalized volume of faces in a simplex of arbitrary dimension. These properties might be of independent interest. We can use them in Section 5.1 to obtain a set of eigenvalues that is relevant for the holomorphy conjecture. Furthermore, we prove that some candidate poles of
$\mathbb{C}$
with respect to their Newton polyhedron at the origin. In Section 2, we recall this notion, along with explicit formulas for the zeta functions in this context. By a formula of Varchenko, the normalized volume of a face gets a key role in the search for eigenvalues of monodromy for nondegenerate singularities. In Section 3, we prove some properties on the normalized volume of faces in a simplex of arbitrary dimension. These properties might be of independent interest. We can use them in Section 5.1 to obtain a set of eigenvalues that is relevant for the holomorphy conjecture. Furthermore, we prove that some candidate poles of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
, respectively
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
, respectively
![]() $Z_{f}(\unicode[STIX]{x1D712},K,s)$
, are not actual poles. This mainly concerns candidate poles contributed by so-called
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
, are not actual poles. This mainly concerns candidate poles contributed by so-called
![]() $B_{1}$
-facets, which were formally introduced in [Reference Lemahieu and Van ProeyenLVP2] in the context of the topological zeta function. In our context of the Igusa zeta function associated to a nontrivial character, some configurations of
$B_{1}$
-facets, which were formally introduced in [Reference Lemahieu and Van ProeyenLVP2] in the context of the topological zeta function. In our context of the Igusa zeta function associated to a nontrivial character, some configurations of
![]() $B_{1}$
-facets that give rise to false poles have been treated in [Reference Bories and VeysBV, Section 9]. It actually turns out that almost all configurations of
$B_{1}$
-facets that give rise to false poles have been treated in [Reference Bories and VeysBV, Section 9]. It actually turns out that almost all configurations of
![]() $B_{1}$
-facets give rise to fake poles (see Section 5.2.3 for the exact statement). We also find a configuration without
$B_{1}$
-facets give rise to fake poles (see Section 5.2.3 for the exact statement). We also find a configuration without
![]() $B_{1}$
-facets where we need to show that the candidate pole is a false pole. Our computations rely on the study of some specific character sums (see Section 4). We can then complete our proof using a nondegeneracy argument (see Lemma 2), which was used for the first time in [Reference Lemahieu and Van ProeyenLVP2].
$B_{1}$
-facets where we need to show that the candidate pole is a false pole. Our computations rely on the study of some specific character sums (see Section 4). We can then complete our proof using a nondegeneracy argument (see Lemma 2), which was used for the first time in [Reference Lemahieu and Van ProeyenLVP2].
As a preliminary remark, we note that for the purpose of proving the holomorphy conjecture one can assume the following.
-
∙
 $f$
has coefficients in the ring of integers
$f$
has coefficients in the ring of integers
 ${\mathcal{O}}_{F}$
of
${\mathcal{O}}_{F}$
of
 $F$
. Indeed, multiplying
$F$
. Indeed, multiplying
 $f$
by a constant
$f$
by a constant
 $a\in F$
affects
$a\in F$
affects
 $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
 $Z_{f}(\unicode[STIX]{x1D712},K,s)$
only for the completions
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
only for the completions
 $K$
in which
$K$
in which
 $\text{ord}(a)\neq 0$
, of which there are finitely many.
$\text{ord}(a)\neq 0$
, of which there are finitely many. -
∙
 $\unicode[STIX]{x1D712}$
is a nontrivial character with conductor equal to
$\unicode[STIX]{x1D712}$
is a nontrivial character with conductor equal to
 $1$
. Indeed, Denef proved that for almost all nonarchimedean completions
$1$
. Indeed, Denef proved that for almost all nonarchimedean completions
 $K$
of
$K$
of
 $F$
, if
$F$
, if
 $\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
is a multiplicative character that is nontrivial on
$\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
is a multiplicative character that is nontrivial on
 $1+P$
, then
$1+P$
, then
 $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
and
 $Z_{f}(\unicode[STIX]{x1D712},K,s)$
are constant on
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
are constant on
 $\mathbb{C}$
(see [Reference DenefD2, Theorem 3.3]).
$\mathbb{C}$
(see [Reference DenefD2, Theorem 3.3]).
From now on we just write
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
) for
$Z_{f}(\unicode[STIX]{x1D712},s)$
) for
![]() $Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
(resp.
$Z_{f,0}(\unicode[STIX]{x1D712},K,s)$
(resp.
![]() $Z_{f}(\unicode[STIX]{x1D712},K,s)$
).
$Z_{f}(\unicode[STIX]{x1D712},K,s)$
).
2 Nondegenerate singularities and their zeta functions
2.1 Nondegenerate singularities
Assume that
![]() $f(\text{}\underline{x})\in {\mathcal{O}}_{F}[\text{}\underline{x}]$
is a nonconstant polynomial satisfying
$f(\text{}\underline{x})\in {\mathcal{O}}_{F}[\text{}\underline{x}]$
is a nonconstant polynomial satisfying
![]() $f(\text{}\underline{0})=0$
. Write
$f(\text{}\underline{0})=0$
. Write
where
![]() $\text{}\underline{k}=(k_{1},\ldots ,k_{n})$
and
$\text{}\underline{k}=(k_{1},\ldots ,k_{n})$
and
![]() $\text{}\underline{x}^{\text{}\underline{k}}=x_{1}^{k_{1}}\cdot \ldots \cdot x_{n}^{k_{n}}$
. The support of
$\text{}\underline{x}^{\text{}\underline{k}}=x_{1}^{k_{1}}\cdot \ldots \cdot x_{n}^{k_{n}}$
. The support of
![]() $f$
is
$f$
is
The Newton polyhedron
![]() $\unicode[STIX]{x1D6E4}_{0}$
of
$\unicode[STIX]{x1D6E4}_{0}$
of
![]() $f$
at the origin is the convex hull in
$f$
at the origin is the convex hull in
![]() $\mathbb{R}_{{\geqslant}0}^{n}$
of
$\mathbb{R}_{{\geqslant}0}^{n}$
of
A facet of the Newton polyhedron is a face of dimension
![]() $n-1$
. For a face
$n-1$
. For a face
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D6E4}_{0}$
, one defines the polynomial
$\unicode[STIX]{x1D6E4}_{0}$
, one defines the polynomial
![]() $f_{\unicode[STIX]{x1D70F}}(\text{}\underline{x}):=\sum _{\text{}\underline{k}\in \mathbb{Z}^{n}\cap \unicode[STIX]{x1D70F}}c_{\text{}\underline{k}}\text{}\underline{x}^{\text{}\underline{k}}$
.
$f_{\unicode[STIX]{x1D70F}}(\text{}\underline{x}):=\sum _{\text{}\underline{k}\in \mathbb{Z}^{n}\cap \unicode[STIX]{x1D70F}}c_{\text{}\underline{k}}\text{}\underline{x}^{\text{}\underline{k}}$
.
We say that the polynomial
![]() $f$
is nondegenerate over
$f$
is nondegenerate over
![]() $\mathbb{C}$
with respect to the compact faces of
$\mathbb{C}$
with respect to the compact faces of
![]() $\unicode[STIX]{x1D6E4}_{0}$
(resp. nondegenerate over
$\unicode[STIX]{x1D6E4}_{0}$
(resp. nondegenerate over
![]() $\mathbb{C}$
with respect to the faces of
$\mathbb{C}$
with respect to the faces of
![]() $\unicode[STIX]{x1D6E4}_{0}$
), if for every compact face
$\unicode[STIX]{x1D6E4}_{0}$
), if for every compact face
![]() $\unicode[STIX]{x1D70F}$
(resp. for every face
$\unicode[STIX]{x1D70F}$
(resp. for every face
![]() $\unicode[STIX]{x1D70F}$
) of
$\unicode[STIX]{x1D70F}$
) of
![]() $\unicode[STIX]{x1D6E4}_{0}$
, the zero locus of
$\unicode[STIX]{x1D6E4}_{0}$
, the zero locus of
![]() $f_{\unicode[STIX]{x1D70F}}$
has no singularities in
$f_{\unicode[STIX]{x1D70F}}$
has no singularities in
![]() $(\mathbb{C}^{\times })^{n}$
. For a fixed Newton polyhedron
$(\mathbb{C}^{\times })^{n}$
. For a fixed Newton polyhedron
![]() $\unicode[STIX]{x1D6E4}$
, almost all polynomials having
$\unicode[STIX]{x1D6E4}$
, almost all polynomials having
![]() $\unicode[STIX]{x1D6E4}$
as their Newton polyhedron are nondegenerate with respect to the faces of
$\unicode[STIX]{x1D6E4}$
as their Newton polyhedron are nondegenerate with respect to the faces of
![]() $\unicode[STIX]{x1D6E4}$
(see [Reference Arnold, Varchenko and Goussein-ZadéAVG, page 157]).
$\unicode[STIX]{x1D6E4}$
(see [Reference Arnold, Varchenko and Goussein-ZadéAVG, page 157]).
Let
![]() $K$
be a nonarchimedean completion of
$K$
be a nonarchimedean completion of
![]() $F$
with valuation ring
$F$
with valuation ring
![]() $R$
and maximal ideal
$R$
and maximal ideal
![]() $P$
, whose residue field we denote by
$P$
, whose residue field we denote by
![]() $\mathbb{F}_{q}$
. Note that
$\mathbb{F}_{q}$
. Note that
![]() ${\mathcal{O}}_{F}\subset R$
, so it makes sense to consider
${\mathcal{O}}_{F}\subset R$
, so it makes sense to consider
![]() $\bar{f}$
, the polynomial over
$\bar{f}$
, the polynomial over
![]() $\mathbb{F}_{q}$
obtained from
$\mathbb{F}_{q}$
obtained from
![]() $f$
by reducing each of its coefficients modulo
$f$
by reducing each of its coefficients modulo
![]() $P$
. We say that
$P$
. We say that
![]() $\bar{f}$
is nondegenerate over
$\bar{f}$
is nondegenerate over
![]() $\mathbb{F}_{q}$
with respect to the compact faces of
$\mathbb{F}_{q}$
with respect to the compact faces of
![]() $\unicode[STIX]{x1D6E4}_{0}$
(resp. nondegenerate over
$\unicode[STIX]{x1D6E4}_{0}$
(resp. nondegenerate over
![]() $\mathbb{F}_{q}$
with respect to the faces of
$\mathbb{F}_{q}$
with respect to the faces of
![]() $\unicode[STIX]{x1D6E4}_{0}$
) if for every compact face
$\unicode[STIX]{x1D6E4}_{0}$
) if for every compact face
![]() $\unicode[STIX]{x1D70F}$
(resp. for every face
$\unicode[STIX]{x1D70F}$
(resp. for every face
![]() $\unicode[STIX]{x1D70F}$
) of
$\unicode[STIX]{x1D70F}$
) of
![]() $\unicode[STIX]{x1D6E4}_{0}$
, the zero locus of
$\unicode[STIX]{x1D6E4}_{0}$
, the zero locus of
![]() $\bar{f_{\unicode[STIX]{x1D70F}}}$
has no singularities in
$\bar{f_{\unicode[STIX]{x1D70F}}}$
has no singularities in
![]() $(\mathbb{F}_{q}^{\times })^{n}$
. If
$(\mathbb{F}_{q}^{\times })^{n}$
. If
![]() $f$
is nondegenerate over
$f$
is nondegenerate over
![]() $\mathbb{C}$
with respect to the compact faces (resp. the faces) of its Newton polyhedron
$\mathbb{C}$
with respect to the compact faces (resp. the faces) of its Newton polyhedron
![]() $\unicode[STIX]{x1D6E4}_{0}$
, then recall that
$\unicode[STIX]{x1D6E4}_{0}$
, then recall that
![]() $\bar{f}$
is nondegenerate over
$\bar{f}$
is nondegenerate over
![]() $\mathbb{F}_{q}$
with respect to the compact faces (resp. the faces) of
$\mathbb{F}_{q}$
with respect to the compact faces (resp. the faces) of
![]() $\unicode[STIX]{x1D6E4}_{0}$
for almost all choices of
$\unicode[STIX]{x1D6E4}_{0}$
for almost all choices of
![]() $K$
. Thus, in order to prove the holomorphy conjecture for polynomials that are nondegenerate over
$K$
. Thus, in order to prove the holomorphy conjecture for polynomials that are nondegenerate over
![]() $\mathbb{C}$
, it suffices to restrict to completions
$\mathbb{C}$
, it suffices to restrict to completions
![]() $K$
for which, moreover,
$K$
for which, moreover,
![]() $\bar{f}$
is nondegenerate over the residue field
$\bar{f}$
is nondegenerate over the residue field
![]() $\mathbb{F}_{q}$
.
$\mathbb{F}_{q}$
.
Further on, we use the following property of nondegeneracy [Reference Lemahieu and Van ProeyenLVP2, Lemma 9].
Lemma 2. If a complex polynomial
![]() $f(x,y,z)$
is nondegenerate with respect to the compact faces of its Newton polyhedron at the origin, then for almost all
$f(x,y,z)$
is nondegenerate with respect to the compact faces of its Newton polyhedron at the origin, then for almost all
![]() $k\in \mathbb{C}$
, the polynomial
$k\in \mathbb{C}$
, the polynomial
![]() $f(x,y,z-k)$
is nondegenerate with respect to the compact faces of its Newton polyhedron at the origin. (Analogously for the variables
$f(x,y,z-k)$
is nondegenerate with respect to the compact faces of its Newton polyhedron at the origin. (Analogously for the variables
![]() $x$
and
$x$
and
![]() $y$
.)
$y$
.)
2.2 Some combinatorial data associated to the Newton polyhedron
Let
![]() $\unicode[STIX]{x1D6E4}_{0}$
be as above. For
$\unicode[STIX]{x1D6E4}_{0}$
be as above. For
![]() $\text{}\underline{a}=(a_{1},\ldots ,a_{n})\in \mathbb{R}_{{\geqslant}0}^{n}$
, we put
$\text{}\underline{a}=(a_{1},\ldots ,a_{n})\in \mathbb{R}_{{\geqslant}0}^{n}$
, we put
All
![]() $F(\text{}\underline{a}),\text{}\underline{a}\neq \text{}\underline{0}$
, are faces of
$F(\text{}\underline{a}),\text{}\underline{a}\neq \text{}\underline{0}$
, are faces of
![]() $\unicode[STIX]{x1D6E4}_{0}$
. To a face
$\unicode[STIX]{x1D6E4}_{0}$
. To a face
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D6E4}_{0}$
we associate its dual cone
$\unicode[STIX]{x1D6E4}_{0}$
we associate its dual cone
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}=\{\text{}\underline{a}\in \mathbb{R}_{{\geqslant}0}^{n}\,\big|\,F(\text{}\underline{a})=\unicode[STIX]{x1D70F}\}$
. It is a rational polyhedral cone of dimension
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}=\{\text{}\underline{a}\in \mathbb{R}_{{\geqslant}0}^{n}\,\big|\,F(\text{}\underline{a})=\unicode[STIX]{x1D70F}\}$
. It is a rational polyhedral cone of dimension
![]() $n-\dim \unicode[STIX]{x1D70F}$
. In particular, if
$n-\dim \unicode[STIX]{x1D70F}$
. In particular, if
![]() $\unicode[STIX]{x1D70F}$
is a facet then
$\unicode[STIX]{x1D70F}$
is a facet then
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
is a ray, say
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
is a ray, say
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}=\text{}\underline{a}\mathbb{R}_{{>}0}$
for some nonzero
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}=\text{}\underline{a}\mathbb{R}_{{>}0}$
for some nonzero
![]() $\text{}\underline{a}\in \mathbb{Z}_{{\geqslant}0}^{n}$
, and then the equation of the hyperplane through
$\text{}\underline{a}\in \mathbb{Z}_{{\geqslant}0}^{n}$
, and then the equation of the hyperplane through
![]() $\unicode[STIX]{x1D70F}$
is
$\unicode[STIX]{x1D70F}$
is
![]() $\text{}\underline{a}\cdot \text{}\underline{x}=N(\text{}\underline{a})$
. If we demand that
$\text{}\underline{a}\cdot \text{}\underline{x}=N(\text{}\underline{a})$
. If we demand that
![]() $\text{}\underline{a}$
is primitive, that is, that
$\text{}\underline{a}$
is primitive, that is, that
![]() $\text{gcd}(a_{1},\ldots ,a_{n})=1$
, then this
$\text{gcd}(a_{1},\ldots ,a_{n})=1$
, then this
![]() $\text{}\underline{a}$
is uniquely defined. For a facet
$\text{}\underline{a}$
is uniquely defined. For a facet
![]() $\unicode[STIX]{x1D70F}$
, we also use the notation
$\unicode[STIX]{x1D70F}$
, we also use the notation
![]() $N(\unicode[STIX]{x1D70F})$
, called the lattice distance of
$N(\unicode[STIX]{x1D70F})$
, called the lattice distance of
![]() $\unicode[STIX]{x1D70F}$
, and
$\unicode[STIX]{x1D70F}$
, and
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})$
, meaning respectively
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})$
, meaning respectively
![]() $N(\text{}\underline{a})$
and
$N(\text{}\underline{a})$
and
![]() $\unicode[STIX]{x1D708}(\text{}\underline{a})$
for this associated
$\unicode[STIX]{x1D708}(\text{}\underline{a})$
for this associated
![]() $\text{}\underline{a}\in \mathbb{Z}_{{\geqslant}0}^{n}$
. For a general proper face
$\text{}\underline{a}\in \mathbb{Z}_{{\geqslant}0}^{n}$
. For a general proper face
![]() $\unicode[STIX]{x1D70F}$
, the dual cone
$\unicode[STIX]{x1D70F}$
, the dual cone
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
is strictly positively spanned by the dual cones of the facets containing
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
is strictly positively spanned by the dual cones of the facets containing
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
For a set of linearly independent vectors
![]() $\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}}\in \mathbb{Z}^{n}$
, we define the multiplicity
$\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}}\in \mathbb{Z}^{n}$
, we define the multiplicity
![]() $\text{mult}(\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}})$
as the index of the lattice
$\text{mult}(\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}})$
as the index of the lattice
![]() $\mathbb{Z}\text{}\underline{a_{1}}+\cdots +\mathbb{Z}\text{}\underline{a_{r}}$
in the group of the points with integral coordinates of the subspace of
$\mathbb{Z}\text{}\underline{a_{1}}+\cdots +\mathbb{Z}\text{}\underline{a_{r}}$
in the group of the points with integral coordinates of the subspace of
![]() $\mathbb{R}^{n}$
generated by
$\mathbb{R}^{n}$
generated by
![]() $\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}}$
. Alternatively,
$\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}}$
. Alternatively,
![]() $\text{mult}(\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}})$
is equal to the greatest common divisor of the determinants of the
$\text{mult}(\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}})$
is equal to the greatest common divisor of the determinants of the
![]() $(r\times r)$
-matrixes obtained by omitting columns from the matrix with rows
$(r\times r)$
-matrixes obtained by omitting columns from the matrix with rows
![]() $\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}}$
. If
$\text{}\underline{a_{1}},\ldots ,\text{}\underline{a_{r}}$
. If
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
is a simplicial cone, then by
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
is a simplicial cone, then by
![]() $\text{mult}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})$
we mean the multiplicity of its set of primitive generators. For a simplicial face
$\text{mult}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})$
we mean the multiplicity of its set of primitive generators. For a simplicial face
![]() $\unicode[STIX]{x1D70F}$
, we write
$\unicode[STIX]{x1D70F}$
, we write
![]() $\text{mult}(\unicode[STIX]{x1D70F})$
for the multiplicity of its set of vertexes.
$\text{mult}(\unicode[STIX]{x1D70F})$
for the multiplicity of its set of vertexes.
2.3 The Igusa zeta function with character for nondegenerate singularities
In the case where
![]() $f\in R[\text{}\underline{x}]$
is nondegenerate over
$f\in R[\text{}\underline{x}]$
is nondegenerate over
![]() $\mathbb{F}_{q}$
with respect to the compact faces (resp. the faces) of its Newton polyhedron at the origin
$\mathbb{F}_{q}$
with respect to the compact faces (resp. the faces) of its Newton polyhedron at the origin
![]() $\unicode[STIX]{x1D6E4}_{0}$
, Hoornaert gave a formula [Reference HoornaertH, Theorem 3.4] for the local (resp. global) Igusa zeta function associated to
$\unicode[STIX]{x1D6E4}_{0}$
, Hoornaert gave a formula [Reference HoornaertH, Theorem 3.4] for the local (resp. global) Igusa zeta function associated to
![]() $f$
and
$f$
and
![]() $\unicode[STIX]{x1D712}$
in terms of
$\unicode[STIX]{x1D712}$
in terms of
![]() $\unicode[STIX]{x1D6E4}_{0}$
, which we recall. Hoornaert states the formula for
$\unicode[STIX]{x1D6E4}_{0}$
, which we recall. Hoornaert states the formula for
![]() $R=\mathbb{Z}_{p}$
only, but her proof generalizes word by word to our more general setting.
$R=\mathbb{Z}_{p}$
only, but her proof generalizes word by word to our more general setting.
Recall that we assume
![]() $\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
to be nontrivial of conductor
$\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
to be nontrivial of conductor
![]() $1$
. Let
$1$
. Let
![]() $pr:R^{\times }\rightarrow \mathbb{F}_{q}^{\times }\cong R^{\times }/(1+P)$
be the natural surjective homomorphism. As
$pr:R^{\times }\rightarrow \mathbb{F}_{q}^{\times }\cong R^{\times }/(1+P)$
be the natural surjective homomorphism. As
![]() $\unicode[STIX]{x1D712}$
is trivial on
$\unicode[STIX]{x1D712}$
is trivial on
![]() $1+P$
, there exists a unique homomorphism
$1+P$
, there exists a unique homomorphism
![]() $\bar{\unicode[STIX]{x1D712}}:\mathbb{F}_{q}^{\times }\rightarrow \mathbb{C}^{\times }$
such that
$\bar{\unicode[STIX]{x1D712}}:\mathbb{F}_{q}^{\times }\rightarrow \mathbb{C}^{\times }$
such that
![]() $\unicode[STIX]{x1D712}=\bar{\unicode[STIX]{x1D712}}\circ pr$
. One formally puts
$\unicode[STIX]{x1D712}=\bar{\unicode[STIX]{x1D712}}\circ pr$
. One formally puts
![]() $\bar{\unicode[STIX]{x1D712}}(0)=0$
. Note that the order of
$\bar{\unicode[STIX]{x1D712}}(0)=0$
. Note that the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of
$\unicode[STIX]{x1D712}$
divides the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
. Let
$\bar{\unicode[STIX]{x1D712}}$
. Let
![]() $f$
be a nonzero polynomial over
$f$
be a nonzero polynomial over
![]() $R$
satisfying
$R$
satisfying
![]() $f(\text{}\underline{0})=0$
, and let
$f(\text{}\underline{0})=0$
, and let
![]() $\bar{f}$
be nondegenerate over
$\bar{f}$
be nondegenerate over
![]() $\mathbb{F}_{q}$
with respect to all the compact faces (resp. all the faces) of its Newton polyhedron
$\mathbb{F}_{q}$
with respect to all the compact faces (resp. all the faces) of its Newton polyhedron
![]() $\unicode[STIX]{x1D6E4}_{0}$
. Let
$\unicode[STIX]{x1D6E4}_{0}$
. Let
Then, Hoornaert proved that the local, respectively global, Igusa zeta function associated to
![]() $f$
and the nontrivial character
$f$
and the nontrivial character
![]() $\unicode[STIX]{x1D712}$
can be computed as
$\unicode[STIX]{x1D712}$
can be computed as
 $$\begin{eqnarray}\displaystyle Z_{f,0}(\unicode[STIX]{x1D712},s) & = & \displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70F}~\text{compact} \\ \text{face of }\unicode[STIX]{x1D6E4}_{0}}}\!L_{\unicode[STIX]{x1D70F}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})(s),\qquad \text{respectively}\qquad \nonumber\\ \displaystyle Z_{f}(\unicode[STIX]{x1D712},s) & = & \displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70F}~\text{face} \\ \text{of }\unicode[STIX]{x1D6E4}_{0}}}\!L_{\unicode[STIX]{x1D70F}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})(s).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{f,0}(\unicode[STIX]{x1D712},s) & = & \displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70F}~\text{compact} \\ \text{face of }\unicode[STIX]{x1D6E4}_{0}}}\!L_{\unicode[STIX]{x1D70F}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})(s),\qquad \text{respectively}\qquad \nonumber\\ \displaystyle Z_{f}(\unicode[STIX]{x1D712},s) & = & \displaystyle \mathop{\sum }_{\substack{ \unicode[STIX]{x1D70F}~\text{face} \\ \text{of }\unicode[STIX]{x1D6E4}_{0}}}\!L_{\unicode[STIX]{x1D70F}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})(s).\nonumber\end{eqnarray}$$
In the last summation, also the face
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6E4}_{0}$
is included, and
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6E4}_{0}$
is included, and
![]() $S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6E4}_{0}})=1$
.
$S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6E4}_{0}})=1$
.
If
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
is simplicial, say (strictly positively) spanned by primitive linearly independent vectors
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
is simplicial, say (strictly positively) spanned by primitive linearly independent vectors
![]() $\text{}\underline{a}_{1},\ldots ,\text{}\underline{a}_{r}\in \mathbb{Z}_{{\geqslant}0}^{n}$
, then
$\text{}\underline{a}_{1},\ldots ,\text{}\underline{a}_{r}\in \mathbb{Z}_{{\geqslant}0}^{n}$
, then
where the sum runs over
![]() $\mathbb{Z}^{n}\cap \{\unicode[STIX]{x1D706}_{1}\text{}\underline{a}_{1}+\cdots +\unicode[STIX]{x1D706}_{r}\text{}\underline{a}_{r}\,\big|\,0\leqslant \unicode[STIX]{x1D706}_{i}<1\}$
. In particular, if
$\mathbb{Z}^{n}\cap \{\unicode[STIX]{x1D706}_{1}\text{}\underline{a}_{1}+\cdots +\unicode[STIX]{x1D706}_{r}\text{}\underline{a}_{r}\,\big|\,0\leqslant \unicode[STIX]{x1D706}_{i}<1\}$
. In particular, if
![]() $\text{mult}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})=1$
, then the numerator is
$\text{mult}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})=1$
, then the numerator is
![]() $1$
. In the nonsimplicial case,
$1$
. In the nonsimplicial case,
![]() $S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})(s)$
is a sum of such expressions (obtained by subdividing
$S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})(s)$
is a sum of such expressions (obtained by subdividing
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
into simplicial cones).
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}}$
into simplicial cones).
We clearly see that the real parts of a set of candidate poles (containing all poles) of the local and global Igusa zeta function are given by the rational numbers
![]() $-\unicode[STIX]{x1D708}(\text{}\underline{a})/N(\text{}\underline{a})$
for
$-\unicode[STIX]{x1D708}(\text{}\underline{a})/N(\text{}\underline{a})$
for
![]() $\text{}\underline{a}$
orthogonal to a facet of the Newton polyhedron at the origin. Moreover, we can restrict to the facets
$\text{}\underline{a}$
orthogonal to a facet of the Newton polyhedron at the origin. Moreover, we can restrict to the facets
![]() $\unicode[STIX]{x1D70F}$
for which the order of
$\unicode[STIX]{x1D70F}$
for which the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
divides
$\bar{\unicode[STIX]{x1D712}}$
divides
![]() $N(\text{}\underline{a})$
, because otherwise
$N(\text{}\underline{a})$
, because otherwise
![]() $L_{\unicode[STIX]{x1D70F}}=0$
. This follows from Lemma 7 below. A fortiori we can restrict to those for which the order of
$L_{\unicode[STIX]{x1D70F}}=0$
. This follows from Lemma 7 below. A fortiori we can restrict to those for which the order of
![]() $\unicode[STIX]{x1D712}$
divides
$\unicode[STIX]{x1D712}$
divides
![]() $N(\text{}\underline{a})$
. We say that such a facet contributes a candidate pole to
$N(\text{}\underline{a})$
. We say that such a facet contributes a candidate pole to
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
, respectively
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
, respectively
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
.
$Z_{f}(\unicode[STIX]{x1D712},s)$
.
We finally remark that if
![]() $f$
is nondegenerate over
$f$
is nondegenerate over
![]() $\mathbb{C}$
with respect to the compact faces of
$\mathbb{C}$
with respect to the compact faces of
![]() $\unicode[STIX]{x1D6E4}_{0}$
, then the couples
$\unicode[STIX]{x1D6E4}_{0}$
, then the couples
![]() $(\unicode[STIX]{x1D708}(\text{}\underline{a}),N(\text{}\underline{a}))$
are part of the numerical data
$(\unicode[STIX]{x1D708}(\text{}\underline{a}),N(\text{}\underline{a}))$
are part of the numerical data
![]() $(\unicode[STIX]{x1D708}_{j},N_{j})$
associated to a very explicit (namely, toric) embedded resolution of
$(\unicode[STIX]{x1D708}_{j},N_{j})$
associated to a very explicit (namely, toric) embedded resolution of
![]() $f^{-1}\{0\}$
over
$f^{-1}\{0\}$
over
![]() $F$
, which was first described by Varchenko in [Reference VarchenkoVa]. Thus, the fact that we can restrict to the case where the order of
$F$
, which was first described by Varchenko in [Reference VarchenkoVa]. Thus, the fact that we can restrict to the case where the order of
![]() $\unicode[STIX]{x1D712}$
divides
$\unicode[STIX]{x1D712}$
divides
![]() $N(\text{}\underline{a})$
also follows from Igusa’s seminal work.
$N(\text{}\underline{a})$
also follows from Igusa’s seminal work.
2.4 The formula of Varchenko for the zeta function of monodromy of
 $f$
in the origin
$f$
in the origin
Let
![]() $f:(\mathbb{C}^{n},0)\rightarrow (\mathbb{C},0)$
be a germ of a holomorphic function. Let
$f:(\mathbb{C}^{n},0)\rightarrow (\mathbb{C},0)$
be a germ of a holomorphic function. Let
![]() ${\mathcal{F}}$
be the Milnor fiber of the Milnor fibration at the origin associated with
${\mathcal{F}}$
be the Milnor fiber of the Milnor fibration at the origin associated with
![]() $f$
, and write
$f$
, and write
![]() $h_{\ast }^{i}:H^{i}({\mathcal{F}},\mathbb{C})\rightarrow H^{i}({\mathcal{F}},\mathbb{C})$
,
$h_{\ast }^{i}:H^{i}({\mathcal{F}},\mathbb{C})\rightarrow H^{i}({\mathcal{F}},\mathbb{C})$
,
![]() $i\geqslant 0$
, for the monodromy transformations.
$i\geqslant 0$
, for the monodromy transformations.
The zeta function of monodromy at the origin associated to
![]() $f$
is
$f$
is
where
![]() $\text{id}^{i}$
is the identical transformation on
$\text{id}^{i}$
is the identical transformation on
![]() $H^{i}({\mathcal{F}},\mathbb{C})$
. One calls
$H^{i}({\mathcal{F}},\mathbb{C})$
. One calls
![]() $\unicode[STIX]{x1D6FC}$
an eigenvalue of monodromy of
$\unicode[STIX]{x1D6FC}$
an eigenvalue of monodromy of
![]() $f$
at the origin if
$f$
at the origin if
![]() $\unicode[STIX]{x1D6FC}$
is an eigenvalue for some
$\unicode[STIX]{x1D6FC}$
is an eigenvalue for some
![]() $h_{\ast }^{i}:H^{i}({\mathcal{F}},\mathbb{C})\rightarrow H^{i}({\mathcal{F}},\mathbb{C})$
. Denef proved that every eigenvalue of monodromy of
$h_{\ast }^{i}:H^{i}({\mathcal{F}},\mathbb{C})\rightarrow H^{i}({\mathcal{F}},\mathbb{C})$
. Denef proved that every eigenvalue of monodromy of
![]() $f$
is a zero or a pole of the zeta function of monodromy at some point of
$f$
is a zero or a pole of the zeta function of monodromy at some point of
![]() $\{f=0\}$
(see [Reference DenefD3]). Varchenko gave in [Reference VarchenkoVa] a formula for
$\{f=0\}$
(see [Reference DenefD3]). Varchenko gave in [Reference VarchenkoVa] a formula for
![]() $\unicode[STIX]{x1D701}_{f,0}$
in terms of
$\unicode[STIX]{x1D701}_{f,0}$
in terms of
![]() $\unicode[STIX]{x1D6E4}_{0}$
if
$\unicode[STIX]{x1D6E4}_{0}$
if
![]() $f$
is nondegenerate with respect to the compact faces of its Newton polyhedron at the origin
$f$
is nondegenerate with respect to the compact faces of its Newton polyhedron at the origin
![]() $\unicode[STIX]{x1D6E4}_{0}$
. He defines a function
$\unicode[STIX]{x1D6E4}_{0}$
. He defines a function
![]() $\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70F}}(t)$
for every compact face
$\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70F}}(t)$
for every compact face
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D6E4}_{0}$
for which there exists a subset
$\unicode[STIX]{x1D6E4}_{0}$
for which there exists a subset
![]() $I\subset \{1,\ldots ,n\}$
with
$I\subset \{1,\ldots ,n\}$
with
![]() $\#I=\text{dim}(\unicode[STIX]{x1D70F})+1$
such that
$\#I=\text{dim}(\unicode[STIX]{x1D70F})+1$
such that
![]() $\unicode[STIX]{x1D70F}\subset L_{I}:=\{x\in \mathbb{R}^{n}\,\big|\,\forall i\not \in I:x_{i}=0\}$
. We call such faces V-faces, and we denote the index set (resp. linear space) corresponding to a V-face
$\unicode[STIX]{x1D70F}\subset L_{I}:=\{x\in \mathbb{R}^{n}\,\big|\,\forall i\not \in I:x_{i}=0\}$
. We call such faces V-faces, and we denote the index set (resp. linear space) corresponding to a V-face
![]() $\unicode[STIX]{x1D70F}$
by
$\unicode[STIX]{x1D70F}$
by
![]() $I_{\unicode[STIX]{x1D70F}}$
(resp.
$I_{\unicode[STIX]{x1D70F}}$
(resp.
![]() $L_{I_{\unicode[STIX]{x1D70F}}}$
). If a V-face is a simplex, then we call it a V-simplex.
$L_{I_{\unicode[STIX]{x1D70F}}}$
). If a V-face is a simplex, then we call it a V-simplex.
For a face
![]() $\unicode[STIX]{x1D70F}$
of dimension 0, we put
$\unicode[STIX]{x1D70F}$
of dimension 0, we put
![]() $\text{Vol}(\unicode[STIX]{x1D70F})=1$
. For every other compact face
$\text{Vol}(\unicode[STIX]{x1D70F})=1$
. For every other compact face
![]() $\unicode[STIX]{x1D70F}$
,
$\unicode[STIX]{x1D70F}$
,
![]() $\text{Vol}(\unicode[STIX]{x1D70F})$
is defined as the volume of
$\text{Vol}(\unicode[STIX]{x1D70F})$
is defined as the volume of
![]() $\unicode[STIX]{x1D70F}$
for the volume form
$\unicode[STIX]{x1D70F}$
for the volume form
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}$
. This is a volume form on
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}$
. This is a volume form on
![]() $\text{Aff}(\unicode[STIX]{x1D70F})$
, the affine space spanned by
$\text{Aff}(\unicode[STIX]{x1D70F})$
, the affine space spanned by
![]() $\unicode[STIX]{x1D70F}$
, such that the parallelepiped spanned by a lattice basis of
$\unicode[STIX]{x1D70F}$
, such that the parallelepiped spanned by a lattice basis of
![]() $\mathbb{Z}^{n}\cap \text{Aff}(\unicode[STIX]{x1D70F})$
has volume 1. The product
$\mathbb{Z}^{n}\cap \text{Aff}(\unicode[STIX]{x1D70F})$
has volume 1. The product
![]() $(\text{dim}\,\unicode[STIX]{x1D70F})!\text{Vol}(\unicode[STIX]{x1D70F})$
is also called the normalized volume of the face
$(\text{dim}\,\unicode[STIX]{x1D70F})!\text{Vol}(\unicode[STIX]{x1D70F})$
is also called the normalized volume of the face
![]() $\unicode[STIX]{x1D70F}$
and is denoted by
$\unicode[STIX]{x1D70F}$
and is denoted by
![]() $\text{NV}(\unicode[STIX]{x1D70F})$
.
$\text{NV}(\unicode[STIX]{x1D70F})$
.
For a V-face
![]() $\unicode[STIX]{x1D70F}$
, let
$\unicode[STIX]{x1D70F}$
, let
![]() $\sum _{i\in I_{\unicode[STIX]{x1D70F}}}a_{i}x_{i}=N(\unicode[STIX]{x1D70F})$
be the equation of
$\sum _{i\in I_{\unicode[STIX]{x1D70F}}}a_{i}x_{i}=N(\unicode[STIX]{x1D70F})$
be the equation of
![]() $\text{Aff}(\unicode[STIX]{x1D70F})$
in
$\text{Aff}(\unicode[STIX]{x1D70F})$
in
![]() $L_{I_{\unicode[STIX]{x1D70F}}}$
, where
$L_{I_{\unicode[STIX]{x1D70F}}}$
, where
![]() $N(\unicode[STIX]{x1D70F})$
and all
$N(\unicode[STIX]{x1D70F})$
and all
![]() $a_{i}$
(for
$a_{i}$
(for
![]() $i\in I_{\unicode[STIX]{x1D70F}}$
) are positive integers, and their greatest common divisor is equal to 1. We put
$i\in I_{\unicode[STIX]{x1D70F}}$
) are positive integers, and their greatest common divisor is equal to 1. We put
In [Reference VarchenkoVa], Varchenko showed that the zeta function of monodromy of
![]() $f$
in the origin is equal to
$f$
in the origin is equal to
where the product runs over all V-faces
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D6E4}_{0}$
.
$\unicode[STIX]{x1D6E4}_{0}$
.
For a fixed facet
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D6E4}_{0}$
, we say that a V-face
$\unicode[STIX]{x1D6E4}_{0}$
, we say that a V-face
![]() $\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D70E}$
in
![]() $\unicode[STIX]{x1D6E4}_{0}$
contributes with respect to
$\unicode[STIX]{x1D6E4}_{0}$
contributes with respect to
![]() $\unicode[STIX]{x1D70F}$
if
$\unicode[STIX]{x1D70F}$
if
![]() $e^{-2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})}$
is a zero of
$e^{-2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})}$
is a zero of
![]() $\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}}(t)$
.
$\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}}(t)$
.
If
![]() $n=3$
, the formula of Varchenko for the zeta function of monodromy at the origin has a specific form which we describe below. We first partition every compact facet into simplices. For each such simplex
$n=3$
, the formula of Varchenko for the zeta function of monodromy at the origin has a specific form which we describe below. We first partition every compact facet into simplices. For each such simplex
![]() $\unicode[STIX]{x1D70F}$
, we define the factor
$\unicode[STIX]{x1D70F}$
, we define the factor
![]() $F_{\unicode[STIX]{x1D70F}}$
as in [Reference Lemahieu and Van ProeyenLVP2]:
$F_{\unicode[STIX]{x1D70F}}$
as in [Reference Lemahieu and Van ProeyenLVP2]:
where the first product runs over the
![]() $1$
-dimensional V-faces
$1$
-dimensional V-faces
![]() $\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D70E}$
in
![]() $\unicode[STIX]{x1D70F}$
and the second product runs over the
$\unicode[STIX]{x1D70F}$
and the second product runs over the
![]() $0$
-dimensional V-faces
$0$
-dimensional V-faces
![]() $p$
of
$p$
of
![]() $\unicode[STIX]{x1D70F}$
that are intersection points of two
$\unicode[STIX]{x1D70F}$
that are intersection points of two
![]() $1$
-dimensional V-faces in
$1$
-dimensional V-faces in
![]() $\unicode[STIX]{x1D70F}$
. In [Reference Lemahieu and Van ProeyenLVP2, Proposition 8], it is shown that
$\unicode[STIX]{x1D70F}$
. In [Reference Lemahieu and Van ProeyenLVP2, Proposition 8], it is shown that
![]() $F_{\unicode[STIX]{x1D70F}}$
is a polynomial. Following the formula of Varchenko, the zeta function of monodromy in the origin can be written as
$F_{\unicode[STIX]{x1D70F}}$
is a polynomial. Following the formula of Varchenko, the zeta function of monodromy in the origin can be written as
where the first product runs over all
![]() $2$
-dimensional simplices
$2$
-dimensional simplices
![]() $\unicode[STIX]{x1D70F}$
obtained after subdividing the compact facets, and the other products run over
$\unicode[STIX]{x1D70F}$
obtained after subdividing the compact facets, and the other products run over
![]() $1$
-dimensional V-faces
$1$
-dimensional V-faces
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $0$
-dimensional V-faces
$0$
-dimensional V-faces
![]() $p$
for which
$p$
for which
![]() $\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}}$
, respectively
$\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}}$
, respectively
![]() $\unicode[STIX]{x1D701}_{p}$
, was not used in any
$\unicode[STIX]{x1D701}_{p}$
, was not used in any
![]() $F_{\unicode[STIX]{x1D70F}}$
.
$F_{\unicode[STIX]{x1D70F}}$
.
3 Preliminary results on the normalized volume
When searching for eigenvalues of monodromy using the formula of Varchenko, one has to compare normalized volumes of compact faces in a facet. This is the motivation for this section. For two faces
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}^{\prime }$
in a simplicial facet
$\unicode[STIX]{x1D70E}^{\prime }$
in a simplicial facet
![]() $\unicode[STIX]{x1D70F}$
, we denote the smallest face containing
$\unicode[STIX]{x1D70F}$
, we denote the smallest face containing
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}^{\prime }$
by
$\unicode[STIX]{x1D70E}^{\prime }$
by
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
.
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
.
Lemma 3. Let
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}^{\prime }$
be two nondisjoint V-faces in a simplicial facet
$\unicode[STIX]{x1D70E}^{\prime }$
be two nondisjoint V-faces in a simplicial facet
![]() $\unicode[STIX]{x1D70F}$
. Then,
$\unicode[STIX]{x1D70F}$
. Then,
![]() $\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }$
and
$\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }$
and
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
are also V-faces.
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
are also V-faces.
Proof. Let
![]() $\unicode[STIX]{x1D70E}$
be a
$\unicode[STIX]{x1D70E}$
be a
![]() $d_{1}$
-dimensional V-simplex, and let
$d_{1}$
-dimensional V-simplex, and let
![]() $\unicode[STIX]{x1D70E}^{\prime }$
be a
$\unicode[STIX]{x1D70E}^{\prime }$
be a
![]() $d_{2}$
-dimensional V-simplex, having
$d_{2}$
-dimensional V-simplex, having
![]() $k$
vertexes in common. Suppose that the vertexes of
$k$
vertexes in common. Suppose that the vertexes of
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
have exactly
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
have exactly
![]() $s$
zero entries in common. Then, one has
$s$
zero entries in common. Then, one has
where (abusing notation)
![]() $\#(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })$
denotes the number of vertexes of
$\#(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })$
denotes the number of vertexes of
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
. On the other hand, the vertexes of
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
. On the other hand, the vertexes of
![]() $\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }$
have at most
$\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }$
have at most
![]() $n-k$
zero entries in common, and so
$n-k$
zero entries in common, and so
Combining these two inequalities, one finds that they are actually equalities, and so
![]() $\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }$
and
$\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }$
and
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
are V-simplices.◻
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
are V-simplices.◻
Recall that for a V-simplex
![]() $\unicode[STIX]{x1D70F}$
, the normalized volume
$\unicode[STIX]{x1D70F}$
, the normalized volume
![]() $\text{NV}(\unicode[STIX]{x1D70F})$
is equal to its multiplicity mult
$\text{NV}(\unicode[STIX]{x1D70F})$
is equal to its multiplicity mult
![]() $(\unicode[STIX]{x1D70F})$
divided by its lattice distance
$(\unicode[STIX]{x1D70F})$
divided by its lattice distance
![]() $N(\unicode[STIX]{x1D70F})$
. Let
$N(\unicode[STIX]{x1D70F})$
. Let
be the vertexes of
![]() $\unicode[STIX]{x1D70F}$
, and let
$\unicode[STIX]{x1D70F}$
, and let
![]() $\unicode[STIX]{x1D70E}$
be a V-face in
$\unicode[STIX]{x1D70E}$
be a V-face in
![]() $\unicode[STIX]{x1D70F}$
with vertexes
$\unicode[STIX]{x1D70F}$
with vertexes
![]() $B^{1},\ldots ,B^{k}$
and
$B^{1},\ldots ,B^{k}$
and
![]() $I_{\unicode[STIX]{x1D70E}}=\{1,\ldots ,k\}$
. Then,
$I_{\unicode[STIX]{x1D70E}}=\{1,\ldots ,k\}$
. Then,
![]() $\text{mult}(\unicode[STIX]{x1D70F})$
is the absolute value of the determinant of the matrix
$\text{mult}(\unicode[STIX]{x1D70F})$
is the absolute value of the determinant of the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}cccccc@{}}B_{1}^{1} & \ldots & B_{k}^{1} & 0 & \ldots & 0\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ B_{1}^{k} & \ldots & B_{k}^{k} & 0 & \ldots & 0\\ \ast & \ldots & \ast & B_{k+1}^{k+1} & \ldots & B_{n}^{k+1}\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ \ast & \ldots & \ast & B_{k+1}^{n} & \ldots & B_{n}^{n}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccccc@{}}B_{1}^{1} & \ldots & B_{k}^{1} & 0 & \ldots & 0\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ B_{1}^{k} & \ldots & B_{k}^{k} & 0 & \ldots & 0\\ \ast & \ldots & \ast & B_{k+1}^{k+1} & \ldots & B_{n}^{k+1}\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ \ast & \ldots & \ast & B_{k+1}^{n} & \ldots & B_{n}^{n}\end{array}\right).\end{eqnarray}$$
We denote the matrix
 $$\begin{eqnarray}M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}:=\left(\begin{array}{@{}ccc@{}}B_{k+1}^{k+1} & \ldots & B_{n}^{k+1}\\ \vdots & \ldots & \vdots \\ B_{k+1}^{n} & \ldots & B_{n}^{n}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}:=\left(\begin{array}{@{}ccc@{}}B_{k+1}^{k+1} & \ldots & B_{n}^{k+1}\\ \vdots & \ldots & \vdots \\ B_{k+1}^{n} & \ldots & B_{n}^{n}\end{array}\right).\end{eqnarray}$$
Then, we have that
![]() $\text{mult}(\unicode[STIX]{x1D70F})=\text{mult}(\unicode[STIX]{x1D70E})\left|\det (M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}})\right|$
.
$\text{mult}(\unicode[STIX]{x1D70F})=\text{mult}(\unicode[STIX]{x1D70E})\left|\det (M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}})\right|$
.
Proposition 4. Let
![]() $\unicode[STIX]{x1D70F}$
be a simplicial facet of a Newton polyhedron in
$\unicode[STIX]{x1D70F}$
be a simplicial facet of a Newton polyhedron in
![]() $\mathbb{R}^{n}$
. If
$\mathbb{R}^{n}$
. If
![]() $\unicode[STIX]{x1D70E}$
is a V-face in
$\unicode[STIX]{x1D70E}$
is a V-face in
![]() $\unicode[STIX]{x1D70F}$
, then
$\unicode[STIX]{x1D70F}$
, then
![]() $\text{NV}(\unicode[STIX]{x1D70E})\mid \text{NV}(\unicode[STIX]{x1D70F})$
.
$\text{NV}(\unicode[STIX]{x1D70E})\mid \text{NV}(\unicode[STIX]{x1D70F})$
.
Proof. Let us denote the equation of the affine space through
![]() $\unicode[STIX]{x1D70F}$
, respectively through
$\unicode[STIX]{x1D70F}$
, respectively through
![]() $\unicode[STIX]{x1D70E}$
, by
$\unicode[STIX]{x1D70E}$
, by
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{Aff}(\unicode[STIX]{x1D70F})\leftrightarrow a_{1}x_{1}+\cdots +a_{n}x_{n}=N(\unicode[STIX]{x1D70F}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{Aff}(\unicode[STIX]{x1D70E})\leftrightarrow \frac{a_{1}x_{1}+\cdots +a_{k}x_{k}}{\gcd (a_{1},\ldots ,a_{k})}=N(\unicode[STIX]{x1D70E}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{Aff}(\unicode[STIX]{x1D70F})\leftrightarrow a_{1}x_{1}+\cdots +a_{n}x_{n}=N(\unicode[STIX]{x1D70F}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{Aff}(\unicode[STIX]{x1D70E})\leftrightarrow \frac{a_{1}x_{1}+\cdots +a_{k}x_{k}}{\gcd (a_{1},\ldots ,a_{k})}=N(\unicode[STIX]{x1D70E}), & \displaystyle \nonumber\end{eqnarray}$$
with
![]() $\gcd (a_{1},\ldots ,a_{n})=1$
and
$\gcd (a_{1},\ldots ,a_{n})=1$
and
![]() $N(\unicode[STIX]{x1D70E})=N(\unicode[STIX]{x1D70F})/\gcd (a_{1},\ldots ,a_{k})$
. Let
$N(\unicode[STIX]{x1D70E})=N(\unicode[STIX]{x1D70F})/\gcd (a_{1},\ldots ,a_{k})$
. Let
be the vertexes of
![]() $\unicode[STIX]{x1D70F}$
, and let
$\unicode[STIX]{x1D70F}$
, and let
![]() $B^{k+1},\ldots ,B^{n}$
be the vertexes of
$B^{k+1},\ldots ,B^{n}$
be the vertexes of
![]() $\unicode[STIX]{x1D70F}$
that are not contained in
$\unicode[STIX]{x1D70F}$
that are not contained in
![]() $\unicode[STIX]{x1D70E}$
. Then, we find that
$\unicode[STIX]{x1D70E}$
. Then, we find that
Let
![]() $v_{j}=(B_{j}^{k+1},\ldots ,B_{j}^{n})^{T},k+1\leqslant j\leqslant n$
, be the
$v_{j}=(B_{j}^{k+1},\ldots ,B_{j}^{n})^{T},k+1\leqslant j\leqslant n$
, be the
![]() $j$
th column of the matrix
$j$
th column of the matrix
![]() $M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}$
, and let
$M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}$
, and let
![]() $\tilde{M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}}$
be the matrix obtained from
$\tilde{M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}}$
be the matrix obtained from
![]() $M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}$
by replacing the first column by
$M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}$
by replacing the first column by
![]() $a_{k+1}v_{k+1}+\cdots +a_{n}v_{n}$
. For every vertex
$a_{k+1}v_{k+1}+\cdots +a_{n}v_{n}$
. For every vertex
![]() $B^{j}$
of
$B^{j}$
of
![]() $\unicode[STIX]{x1D70F}$
, we have that
$\unicode[STIX]{x1D70F}$
, we have that
![]() $\gcd (a_{1},\ldots ,a_{k})\mid a_{k+1}B_{k+1}^{j}+\cdots +a_{n}B_{n}^{j}$
, and hence we find that
$\gcd (a_{1},\ldots ,a_{k})\mid a_{k+1}B_{k+1}^{j}+\cdots +a_{n}B_{n}^{j}$
, and hence we find that
![]() $\gcd (a_{1},\ldots ,a_{k})\mid \det (\tilde{M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}})=a_{k+1}\det (M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}})$
. Analogously, we obtain that
$\gcd (a_{1},\ldots ,a_{k})\mid \det (\tilde{M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}}})=a_{k+1}\det (M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}})$
. Analogously, we obtain that
![]() $\gcd (a_{1},\ldots ,a_{k})\mid a_{j}\det (M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}})$
, for
$\gcd (a_{1},\ldots ,a_{k})\mid a_{j}\det (M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}})$
, for
![]() $k+1\leqslant j\leqslant n$
. As we suppose that
$k+1\leqslant j\leqslant n$
. As we suppose that
![]() $\gcd (a_{1},\ldots ,a_{n})=1$
, we get that
$\gcd (a_{1},\ldots ,a_{n})=1$
, we get that
![]() $\gcd (a_{1},\ldots ,a_{k})\mid \text{det}(M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}})$
, which implies that
$\gcd (a_{1},\ldots ,a_{k})\mid \text{det}(M_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}})$
, which implies that
![]() $\text{NV}(\unicode[STIX]{x1D70E})\mid \text{NV}(\unicode[STIX]{x1D70F})$
.◻
$\text{NV}(\unicode[STIX]{x1D70E})\mid \text{NV}(\unicode[STIX]{x1D70F})$
.◻
Proposition 5. Let
![]() $\unicode[STIX]{x1D70F}$
be a simplicial facet of a Newton polyhedron in
$\unicode[STIX]{x1D70F}$
be a simplicial facet of a Newton polyhedron in
![]() $\mathbb{R}^{n}$
. If
$\mathbb{R}^{n}$
. If
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}^{\prime }$
are V-faces in
$\unicode[STIX]{x1D70E}^{\prime }$
are V-faces in
![]() $\unicode[STIX]{x1D70F}$
such that
$\unicode[STIX]{x1D70F}$
such that
![]() $\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }\neq \emptyset$
, then
$\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }\neq \emptyset$
, then
Moreover, if
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }=\unicode[STIX]{x1D70F}$
, then
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }=\unicode[STIX]{x1D70F}$
, then
![]() $M=1$
if and only if
$M=1$
if and only if
Proof. As
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
is also a V-face (see Lemma 3), it follows by Proposition 4 that it is sufficient to prove that
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }$
is also a V-face (see Lemma 3), it follows by Proposition 4 that it is sufficient to prove that
Let
![]() $B^{1},\ldots ,B^{k},B^{k+1},\ldots ,B^{r}$
be the vertexes of
$B^{1},\ldots ,B^{k},B^{k+1},\ldots ,B^{r}$
be the vertexes of
![]() $\unicode[STIX]{x1D70E}$
, and let
$\unicode[STIX]{x1D70E}$
, and let
![]() $B^{1},\ldots ,B^{k},B^{r+1},\ldots ,B^{s}$
be the vertexes of
$B^{1},\ldots ,B^{k},B^{r+1},\ldots ,B^{s}$
be the vertexes of
![]() $\unicode[STIX]{x1D70E}^{\prime }$
. Then,
$\unicode[STIX]{x1D70E}^{\prime }$
. Then,
![]() $\text{mult}(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })$
is the absolute value of the determinant of the matrix
$\text{mult}(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })$
is the absolute value of the determinant of the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccccccc@{}}B_{1}^{1} & \ldots & B_{k}^{1} & 0 & \ldots & 0 & 0 & \ldots & 0\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ B_{1}^{k} & \ldots & B_{k}^{k} & 0 & \ldots & 0 & 0 & \ldots & 0\\ \ast & \ldots & \ast & B_{k+1}^{k+1} & \ldots & B_{r}^{k+1} & 0 & \ldots & 0\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ \ast & \ldots & \ast & B_{k+1}^{r} & \ldots & B_{r}^{r} & 0 & \ldots & 0\\ \ast & \ldots & \ast & 0 & \ldots & 0 & B_{r+1}^{r+1} & \ldots & B_{s}^{r+1}\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ \ast & \ldots & \ast & 0 & \ldots & 0 & B_{r+1}^{s} & \ldots & B_{s}^{s}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccccccc@{}}B_{1}^{1} & \ldots & B_{k}^{1} & 0 & \ldots & 0 & 0 & \ldots & 0\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ B_{1}^{k} & \ldots & B_{k}^{k} & 0 & \ldots & 0 & 0 & \ldots & 0\\ \ast & \ldots & \ast & B_{k+1}^{k+1} & \ldots & B_{r}^{k+1} & 0 & \ldots & 0\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ \ast & \ldots & \ast & B_{k+1}^{r} & \ldots & B_{r}^{r} & 0 & \ldots & 0\\ \ast & \ldots & \ast & 0 & \ldots & 0 & B_{r+1}^{r+1} & \ldots & B_{s}^{r+1}\\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ \ast & \ldots & \ast & 0 & \ldots & 0 & B_{r+1}^{s} & \ldots & B_{s}^{s}\end{array}\right).\end{eqnarray}$$
We write
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{Aff}(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })\leftrightarrow a_{1}x_{1}+\cdots +a_{s}x_{s}=N(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }),\quad \text{with }\gcd (a_{1},\ldots ,a_{s})=1, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FC}:=\gcd (a_{1},\ldots ,a_{k}),\qquad & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}:=\gcd (a_{k+1},\ldots ,a_{r})\qquad \text{and}\qquad \unicode[STIX]{x1D6FE}:=\gcd (a_{r+1},\ldots ,a_{s}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{Aff}(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })\leftrightarrow a_{1}x_{1}+\cdots +a_{s}x_{s}=N(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }),\quad \text{with }\gcd (a_{1},\ldots ,a_{s})=1, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FC}:=\gcd (a_{1},\ldots ,a_{k}),\qquad & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}:=\gcd (a_{k+1},\ldots ,a_{r})\qquad \text{and}\qquad \unicode[STIX]{x1D6FE}:=\gcd (a_{r+1},\ldots ,a_{s}). & \displaystyle \nonumber\end{eqnarray}$$
Then, we have
 $$\begin{eqnarray}\displaystyle \text{Aff}(\unicode[STIX]{x1D70E}) & \leftrightarrow & \displaystyle \frac{a_{1}x_{1}+\cdots +a_{k}x_{k}+a_{k+1}x_{k+1}+\cdots +a_{r}x_{r}}{\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}\nonumber\\ \displaystyle & = & \displaystyle \frac{N(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })}{\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}=N(\unicode[STIX]{x1D70E}),\nonumber\\ \displaystyle \text{Aff}(\unicode[STIX]{x1D70E}^{\prime }) & \leftrightarrow & \displaystyle \frac{a_{1}x_{1}+\cdots +a_{k}x_{k}+a_{r+1}x_{r+1}+\cdots +a_{s}x_{s}}{\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE})}\nonumber\\ \displaystyle & = & \displaystyle \frac{N(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })}{\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE})}=N(\unicode[STIX]{x1D70E}^{\prime }),\nonumber\\ \displaystyle \text{Aff}(\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }) & \leftrightarrow & \displaystyle \frac{a_{1}x_{1}+\cdots +a_{k}x_{k}}{\unicode[STIX]{x1D6FC}}=\frac{N(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })}{\unicode[STIX]{x1D6FC}}=N(\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Aff}(\unicode[STIX]{x1D70E}) & \leftrightarrow & \displaystyle \frac{a_{1}x_{1}+\cdots +a_{k}x_{k}+a_{k+1}x_{k+1}+\cdots +a_{r}x_{r}}{\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}\nonumber\\ \displaystyle & = & \displaystyle \frac{N(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })}{\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})}=N(\unicode[STIX]{x1D70E}),\nonumber\\ \displaystyle \text{Aff}(\unicode[STIX]{x1D70E}^{\prime }) & \leftrightarrow & \displaystyle \frac{a_{1}x_{1}+\cdots +a_{k}x_{k}+a_{r+1}x_{r+1}+\cdots +a_{s}x_{s}}{\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE})}\nonumber\\ \displaystyle & = & \displaystyle \frac{N(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })}{\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE})}=N(\unicode[STIX]{x1D70E}^{\prime }),\nonumber\\ \displaystyle \text{Aff}(\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }) & \leftrightarrow & \displaystyle \frac{a_{1}x_{1}+\cdots +a_{k}x_{k}}{\unicode[STIX]{x1D6FC}}=\frac{N(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime })}{\unicode[STIX]{x1D6FC}}=N(\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }).\nonumber\end{eqnarray}$$
By using Proposition 4, we get
As
![]() $\text{gcd}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=1$
, the quotient
$\text{gcd}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=1$
, the quotient
![]() $\unicode[STIX]{x1D6FC}/(\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}))$
is an integer.
$\unicode[STIX]{x1D6FC}/(\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\gcd (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}))$
is an integer.
To prove the second statement, let
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}^{\prime }$
be two V-faces in a simplicial facet
$\unicode[STIX]{x1D70E}^{\prime }$
be two V-faces in a simplicial facet
![]() $\unicode[STIX]{x1D70F}$
such that
$\unicode[STIX]{x1D70F}$
such that
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }=\unicode[STIX]{x1D70F}$
. Then, one easily shows that
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{\prime }=\unicode[STIX]{x1D70F}$
. Then, one easily shows that
![]() $N(\unicode[STIX]{x1D70F})=\text{lcm}(N(\unicode[STIX]{x1D70E}),N(\unicode[STIX]{x1D70E}^{\prime }))$
, and one can then write
$N(\unicode[STIX]{x1D70F})=\text{lcm}(N(\unicode[STIX]{x1D70E}),N(\unicode[STIX]{x1D70E}^{\prime }))$
, and one can then write
Corollary 6. Let
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}^{\prime }$
be two V-faces in a simplicial facet
$\unicode[STIX]{x1D70E}^{\prime }$
be two V-faces in a simplicial facet
![]() $\unicode[STIX]{x1D70F}$
. If
$\unicode[STIX]{x1D70F}$
. If
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}^{\prime }$
contribute with respect to
$\unicode[STIX]{x1D70E}^{\prime }$
contribute with respect to
![]() $\unicode[STIX]{x1D70F}$
, and if
$\unicode[STIX]{x1D70F}$
, and if
![]() $\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }$
does not, then
$\unicode[STIX]{x1D70E}\cap \unicode[STIX]{x1D70E}^{\prime }$
does not, then
![]() $M\geqslant 2$
in Equation (4).
$M\geqslant 2$
in Equation (4).
4 Some character sums
In order to prove the holomorphy conjecture, we have to show that some candidate poles of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
) are false poles. These proofs rely on the computation of certain character sums. We first recall some well-known properties of character sums over finite fields which we need when treating
$Z_{f}(\unicode[STIX]{x1D712},s)$
) are false poles. These proofs rely on the computation of certain character sums. We first recall some well-known properties of character sums over finite fields which we need when treating
![]() $B_{1}$
-facets. We then study a specific character sum (see Proposition 10), which shows up when proving fakeness of some other candidate pole.
$B_{1}$
-facets. We then study a specific character sum (see Proposition 10), which shows up when proving fakeness of some other candidate pole.
Lemma 7. Let
![]() $a_{1},\ldots ,a_{n},N\in \mathbb{Z}$
, and let
$a_{1},\ldots ,a_{n},N\in \mathbb{Z}$
, and let
![]() $\unicode[STIX]{x1D712}$
be a multiplicative character of
$\unicode[STIX]{x1D712}$
be a multiplicative character of
![]() $\mathbb{F}_{q}^{\times }$
whose order is not a divisor of
$\mathbb{F}_{q}^{\times }$
whose order is not a divisor of
![]() $N$
. Let
$N$
. Let
![]() $f\in \mathbb{F}_{q}[x_{1},\ldots ,x_{n}]$
be such that each exponent
$f\in \mathbb{F}_{q}[x_{1},\ldots ,x_{n}]$
be such that each exponent
![]() $(k_{1},\ldots ,k_{n})$
appearing in
$(k_{1},\ldots ,k_{n})$
appearing in
![]() $f$
satisfies
$f$
satisfies
![]() $a_{1}k_{1}+\cdots +a_{n}k_{n}=N$
. Then,
$a_{1}k_{1}+\cdots +a_{n}k_{n}=N$
. Then,
Proof. Pick
![]() $u\in \mathbb{F}_{q}^{\times }$
such that
$u\in \mathbb{F}_{q}^{\times }$
such that
![]() $\unicode[STIX]{x1D712}(u^{N})\neq 1$
. Then, the left-hand side equals
$\unicode[STIX]{x1D712}(u^{N})\neq 1$
. Then, the left-hand side equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{(x_{1},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n}}\unicode[STIX]{x1D712}(f(u^{a_{1}}x_{1},\ldots ,u^{a_{n}}x_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D712}\left(u^{N}\right)\mathop{\sum }_{(x_{1},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n}}\unicode[STIX]{x1D712}(f(x_{1},\ldots ,x_{n})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{(x_{1},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n}}\unicode[STIX]{x1D712}(f(u^{a_{1}}x_{1},\ldots ,u^{a_{n}}x_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D712}\left(u^{N}\right)\mathop{\sum }_{(x_{1},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n}}\unicode[STIX]{x1D712}(f(x_{1},\ldots ,x_{n})),\nonumber\end{eqnarray}$$
from which the property follows. ◻
Lemma 8. Let
![]() $a\in \mathbb{N}$
, and let
$a\in \mathbb{N}$
, and let
![]() $\unicode[STIX]{x1D712}$
be a multiplicative character of
$\unicode[STIX]{x1D712}$
be a multiplicative character of
![]() $\mathbb{F}_{q}^{\times }$
whose order is not a divisor of
$\mathbb{F}_{q}^{\times }$
whose order is not a divisor of
![]() $a$
, then
$a$
, then
![]() $\sum _{x\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(x^{a})=0$
.
$\sum _{x\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(x^{a})=0$
.
Proof. Take
![]() $f(x)=x^{a}$
in the previous lemma.◻
$f(x)=x^{a}$
in the previous lemma.◻
Lemma 9. Let
![]() $f$
be a polynomial, let
$f$
be a polynomial, let
![]() $g$
be a monomial (possibly equipped with a nonzero coefficient) over
$g$
be a monomial (possibly equipped with a nonzero coefficient) over
![]() $\mathbb{F}_{q}$
in the variables
$\mathbb{F}_{q}$
in the variables
![]() $x_{2},\ldots ,x_{n}$
, and let
$x_{2},\ldots ,x_{n}$
, and let
![]() $\unicode[STIX]{x1D712}$
be a nontrivial multiplicative character of
$\unicode[STIX]{x1D712}$
be a nontrivial multiplicative character of
![]() $\mathbb{F}_{q}^{\times }$
. Then,
$\mathbb{F}_{q}^{\times }$
. Then,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{(x_{1},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n}}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})+x_{1}g(x_{2},\ldots ,x_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad =-\mathop{\sum }_{(x_{2},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n-1}}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{(x_{1},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n}}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})+x_{1}g(x_{2},\ldots ,x_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad =-\mathop{\sum }_{(x_{2},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n-1}}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})).\nonumber\end{eqnarray}$$
Proof. One can write
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{(x_{1},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n}}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})+x_{1}g(x_{2},\ldots ,x_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{(x_{2},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n-1}}\mathop{\sum }_{x_{1}\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})+x_{1}g(x_{2},\ldots ,x_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{(x_{2},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n-1}}\left(\mathop{\sum }_{u\in \mathbb{F}_{q}}\unicode[STIX]{x1D712}(u)-\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n}))\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-\mathop{\sum }_{(x_{2},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n-1}}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{(x_{1},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n}}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})+x_{1}g(x_{2},\ldots ,x_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{(x_{2},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n-1}}\mathop{\sum }_{x_{1}\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})+x_{1}g(x_{2},\ldots ,x_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{(x_{2},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n-1}}\left(\mathop{\sum }_{u\in \mathbb{F}_{q}}\unicode[STIX]{x1D712}(u)-\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n}))\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-\mathop{\sum }_{(x_{2},\ldots ,x_{n})\in (\mathbb{F}_{q}^{\times })^{n-1}}\unicode[STIX]{x1D712}(f(x_{2},\ldots ,x_{n})),\nonumber\end{eqnarray}$$
where we use Lemma 8 in the last step. ◻
Proposition 10. Let
![]() $\unicode[STIX]{x1D712}$
be a multiplicative character of
$\unicode[STIX]{x1D712}$
be a multiplicative character of
![]() $\mathbb{F}_{q}^{\times }$
such that its order does not divide
$\mathbb{F}_{q}^{\times }$
such that its order does not divide
![]() $a\in \mathbb{N}$
. Let
$a\in \mathbb{N}$
. Let
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}\in \mathbb{F}_{q}$
, and let
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}\in \mathbb{F}_{q}$
, and let
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}\in \mathbb{F}_{q}^{\times }$
be such that
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}\in \mathbb{F}_{q}^{\times }$
be such that
![]() $\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\neq 0$
. Then,
$\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\neq 0$
. Then,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{(x,y,z)\in (\mathbb{F}_{q}^{\times })^{3}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2}+\unicode[STIX]{x1D6FE}x^{(x_{1}+x_{2})/2}yz+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2})\nonumber\\ \displaystyle & & \displaystyle \qquad =-\,\mathop{\sum }_{(x,y)\in (\mathbb{F}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2})-\mathop{\sum }_{(x,z)\in (\mathbb{F}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{(x,y,z)\in (\mathbb{F}_{q}^{\times })^{3}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2}+\unicode[STIX]{x1D6FE}x^{(x_{1}+x_{2})/2}yz+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2})\nonumber\\ \displaystyle & & \displaystyle \qquad =-\,\mathop{\sum }_{(x,y)\in (\mathbb{F}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2})-\mathop{\sum }_{(x,z)\in (\mathbb{F}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2}),\nonumber\end{eqnarray}$$
with
![]() $x_{1},x_{2}\in \mathbb{N}$
such that
$x_{1},x_{2}\in \mathbb{N}$
such that
![]() $x_{1}\equiv x_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}2$
.
$x_{1}\equiv x_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}2$
.
Proof. First assume that
![]() $q$
is odd, and write
$q$
is odd, and write
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}$
. Let
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}$
. Let
For each
![]() $c\in \mathbb{F}_{q}^{\times }$
, define
$c\in \mathbb{F}_{q}^{\times }$
, define
 $$\begin{eqnarray}\displaystyle & \displaystyle L_{c}:=\#\{(x,y,z)\in (\mathbb{F}_{q}^{\times })^{3}\,\big|\,\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2}+\unicode[STIX]{x1D6FE}x^{(x_{1}+x_{2})/2}yz+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2}=c\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle N_{y,c}:=\#\{(x,y)\in (\mathbb{F}_{q}^{\times })^{2}\,\big|\,\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2}=c\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle N_{z,c}:=\#\{(x,z)\in (\mathbb{F}_{q}^{\times })^{2}\,\big|\,\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2}=c\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{c}:=\#\{x\in \mathbb{F}_{q}^{\times }\,\big|\,\unicode[STIX]{x1D6FC}x^{a}=c\}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle L_{c}:=\#\{(x,y,z)\in (\mathbb{F}_{q}^{\times })^{3}\,\big|\,\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2}+\unicode[STIX]{x1D6FE}x^{(x_{1}+x_{2})/2}yz+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2}=c\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle N_{y,c}:=\#\{(x,y)\in (\mathbb{F}_{q}^{\times })^{2}\,\big|\,\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2}=c\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle N_{z,c}:=\#\{(x,z)\in (\mathbb{F}_{q}^{\times })^{2}\,\big|\,\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2}=c\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{c}:=\#\{x\in \mathbb{F}_{q}^{\times }\,\big|\,\unicode[STIX]{x1D6FC}x^{a}=c\}. & \displaystyle \nonumber\end{eqnarray}$$
We rewrite the first equation as
For each value of
![]() $x\in \mathbb{F}_{q}^{\times }$
, this defines a conic in the variables
$x\in \mathbb{F}_{q}^{\times }$
, this defines a conic in the variables
![]() $y$
and
$y$
and
![]() $z$
. The discriminant of the quadratic part equals
$z$
. The discriminant of the quadratic part equals
![]() $\unicode[STIX]{x1D6E5}\cdot x^{x_{1}+x_{2}}\neq 0$
. As we suppose
$\unicode[STIX]{x1D6E5}\cdot x^{x_{1}+x_{2}}\neq 0$
. As we suppose
![]() $x_{1}\equiv x_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}2$
, we have that
$x_{1}\equiv x_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}2$
, we have that
![]() $\unicode[STIX]{x1D6E5}\cdot x^{x_{1}+x_{2}}$
is a square if and only if
$\unicode[STIX]{x1D6E5}\cdot x^{x_{1}+x_{2}}$
is a square if and only if
![]() $\unicode[STIX]{x1D6E5}$
is a square. In the
$\unicode[STIX]{x1D6E5}$
is a square. In the
![]() $M_{c}$
cases where
$M_{c}$
cases where
![]() $c-\unicode[STIX]{x1D6FC}x^{a}=0$
, the conic degenerates either into two lines over
$c-\unicode[STIX]{x1D6FC}x^{a}=0$
, the conic degenerates either into two lines over
![]() $\mathbb{F}_{q}$
(if
$\mathbb{F}_{q}$
(if
![]() $\unicode[STIX]{x1D6E5}$
is a square), or into two conjugate lines over
$\unicode[STIX]{x1D6E5}$
is a square), or into two conjugate lines over
![]() $\mathbb{F}_{q^{2}}$
(if
$\mathbb{F}_{q^{2}}$
(if
![]() $\unicode[STIX]{x1D6E5}$
is a nonsquare). Thus, in this case it carries
$\unicode[STIX]{x1D6E5}$
is a nonsquare). Thus, in this case it carries
![]() $\unicode[STIX]{x1D700}(q-1)+1$
points
$\unicode[STIX]{x1D700}(q-1)+1$
points
![]() $(y,z)\in \mathbb{F}_{q}^{2}$
. If
$(y,z)\in \mathbb{F}_{q}^{2}$
. If
![]() $c-\unicode[STIX]{x1D6FC}x^{a}\neq 0$
, then one verifies using
$c-\unicode[STIX]{x1D6FC}x^{a}\neq 0$
, then one verifies using
![]() $\unicode[STIX]{x1D6E5}\neq 0$
that Equation (5) defines an absolutely irreducible conic. It has
$\unicode[STIX]{x1D6E5}\neq 0$
that Equation (5) defines an absolutely irreducible conic. It has
![]() $\unicode[STIX]{x1D700}$
rational points at infinity, so we conclude that the conic carries
$\unicode[STIX]{x1D700}$
rational points at infinity, so we conclude that the conic carries
![]() $q+1-\unicode[STIX]{x1D700}$
points in
$q+1-\unicode[STIX]{x1D700}$
points in
![]() $\mathbb{F}_{q}^{2}$
, because every projective nonsingular curve of genus
$\mathbb{F}_{q}^{2}$
, because every projective nonsingular curve of genus
![]() $0$
over a finite field
$0$
over a finite field
![]() $\mathbb{F}_{q}$
has
$\mathbb{F}_{q}$
has
![]() $q+1$
rational points (see [Reference Fried and JardenFJ]). Overall, we count
$q+1$
rational points (see [Reference Fried and JardenFJ]). Overall, we count
solutions
![]() $(x,y,z)\in \mathbb{F}_{q}^{\times }\times \mathbb{F}_{q}^{2}$
to Equation (5). This includes
$(x,y,z)\in \mathbb{F}_{q}^{\times }\times \mathbb{F}_{q}^{2}$
to Equation (5). This includes
![]() $M_{c}$
points of the form
$M_{c}$
points of the form
![]() $(x,0,0)$
,
$(x,0,0)$
,
![]() $N_{y,c}$
points of the form
$N_{y,c}$
points of the form
![]() $(x,y,0)$
with
$(x,y,0)$
with
![]() $y\neq 0$
, and
$y\neq 0$
, and
![]() $N_{z,c}$
points of the form
$N_{z,c}$
points of the form
![]() $(x,0,z)$
with
$(x,0,z)$
with
![]() $z\neq 0$
. Therefore,
$z\neq 0$
. Therefore,
Summing up, for some constants
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D707}$
that do not depend on
$\unicode[STIX]{x1D707}$
that do not depend on
![]() $c$
, it holds that
$c$
, it holds that
![]() $L_{c}=-N_{y,c}-N_{z,c}+\unicode[STIX]{x1D706}M_{c}+\unicode[STIX]{x1D707}$
. Now note that
$L_{c}=-N_{y,c}-N_{z,c}+\unicode[STIX]{x1D706}M_{c}+\unicode[STIX]{x1D707}$
. Now note that
 $$\begin{eqnarray}\displaystyle & \displaystyle S_{1}:=\mathop{\sum }_{(x,y,z)\in (\mathbb{F}_{q}^{\times })^{3}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2}+\unicode[STIX]{x1D6FE}x^{(x_{1}+x_{2})/2}yz+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2})=\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}L_{c}\unicode[STIX]{x1D712}(c), & \displaystyle \nonumber\\ \displaystyle & \displaystyle S_{y}:=\mathop{\sum }_{(x,y)\in (\mathbb{F}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2})=\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}N_{y,c}\unicode[STIX]{x1D712}(c), & \displaystyle \nonumber\\ \displaystyle & \displaystyle S_{z}:=\mathop{\sum }_{(x,z)\in (\mathbb{F}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2})=\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}N_{z,c}\unicode[STIX]{x1D712}(c), & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC})\mathop{\sum }_{x\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(x^{a})=\mathop{\sum }_{x\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a})=\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}M_{c}\unicode[STIX]{x1D712}(c). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle S_{1}:=\mathop{\sum }_{(x,y,z)\in (\mathbb{F}_{q}^{\times })^{3}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2}+\unicode[STIX]{x1D6FE}x^{(x_{1}+x_{2})/2}yz+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2})=\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}L_{c}\unicode[STIX]{x1D712}(c), & \displaystyle \nonumber\\ \displaystyle & \displaystyle S_{y}:=\mathop{\sum }_{(x,y)\in (\mathbb{F}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FD}x^{x_{2}}y^{2})=\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}N_{y,c}\unicode[STIX]{x1D712}(c), & \displaystyle \nonumber\\ \displaystyle & \displaystyle S_{z}:=\mathop{\sum }_{(x,z)\in (\mathbb{F}_{q}^{\times })^{2}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a}+\unicode[STIX]{x1D6FF}x^{x_{1}}z^{2})=\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}N_{z,c}\unicode[STIX]{x1D712}(c), & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC})\mathop{\sum }_{x\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(x^{a})=\mathop{\sum }_{x\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}x^{a})=\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}M_{c}\unicode[STIX]{x1D712}(c). & \displaystyle \nonumber\end{eqnarray}$$
As for the last line, the first equality follows by Lemma 8. Plugging in the expression for
![]() $L_{c}$
in
$L_{c}$
in
![]() $S_{1}$
, we find
$S_{1}$
, we find
 $$\begin{eqnarray}\displaystyle S_{1} & = & \displaystyle -\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}N_{y,c}\unicode[STIX]{x1D712}(c)-\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}N_{z,c}\unicode[STIX]{x1D712}(c)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}M_{c}\unicode[STIX]{x1D712}(c)+\unicode[STIX]{x1D707}\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(c)=-S_{y}-S_{z},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{1} & = & \displaystyle -\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}N_{y,c}\unicode[STIX]{x1D712}(c)-\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}N_{z,c}\unicode[STIX]{x1D712}(c)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}M_{c}\unicode[STIX]{x1D712}(c)+\unicode[STIX]{x1D707}\mathop{\sum }_{c\in \mathbb{F}_{q}^{\times }}\unicode[STIX]{x1D712}(c)=-S_{y}-S_{z},\nonumber\end{eqnarray}$$
as wanted.
If
![]() $q$
is even, then our condition
$q$
is even, then our condition
![]() $\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\neq 0$
amounts to
$\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\neq 0$
amounts to
![]() $\unicode[STIX]{x1D6FE}\neq 0$
. The above proof still applies, except that one should now work with
$\unicode[STIX]{x1D6FE}\neq 0$
. The above proof still applies, except that one should now work with
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FE}^{2}$
, and the definition of
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FE}^{2}$
, and the definition of
![]() $\unicode[STIX]{x1D700}$
should be modified to
$\unicode[STIX]{x1D700}$
should be modified to
For this definition of
![]() $\unicode[STIX]{x1D700}$
, one verifies that Equation (6) still holds (see [Reference Berlekamp, Rumsey and SolomonBRS, Theorem 1]), and the remainder of the proof is exactly the same.◻
$\unicode[STIX]{x1D700}$
, one verifies that Equation (6) still holds (see [Reference Berlekamp, Rumsey and SolomonBRS, Theorem 1]), and the remainder of the proof is exactly the same.◻
Note that the exponents
![]() $(a,0,0)$
,
$(a,0,0)$
,
![]() $(x_{1},0,2)$
,
$(x_{1},0,2)$
,
![]() $((x_{1}+x_{2})/2,1,1)$
,
$((x_{1}+x_{2})/2,1,1)$
,
![]() $(x_{2},2,0)$
are all contained in the hyperplane
$(x_{2},2,0)$
are all contained in the hyperplane
![]() $2k_{1}+(a-x_{2})k_{2}+(a-x_{1})k_{3}=2a$
, so under the stronger assumption that the order of
$2k_{1}+(a-x_{2})k_{2}+(a-x_{1})k_{3}=2a$
, so under the stronger assumption that the order of
![]() $\unicode[STIX]{x1D712}$
does not divide
$\unicode[STIX]{x1D712}$
does not divide
![]() $2a$
, or under the additional assumption that
$2a$
, or under the additional assumption that
![]() $a-x_{1}$
is even (which holds if and only if
$a-x_{1}$
is even (which holds if and only if
![]() $a-x_{2}$
is even), we see from Lemma 7 that all sums in the statement of the proposition are actually zero.
$a-x_{2}$
is even), we see from Lemma 7 that all sums in the statement of the proposition are actually zero.
5 A proof of the holomorphy conjecture for nondegenerate surface singularities
Let
![]() $f(\text{}\underline{x})$
be as in Section 2.1, and assume that it is nondegenerate over
$f(\text{}\underline{x})$
be as in Section 2.1, and assume that it is nondegenerate over
![]() $\mathbb{C}$
with respect to the compact faces (resp. the faces) of its Newton polyhedron at the origin
$\mathbb{C}$
with respect to the compact faces (resp. the faces) of its Newton polyhedron at the origin
![]() $\unicode[STIX]{x1D6E4}_{0}$
. Let
$\unicode[STIX]{x1D6E4}_{0}$
. Let
![]() $K$
be a nonarchimedean completion with valuation ring
$K$
be a nonarchimedean completion with valuation ring
![]() $R$
and residue field
$R$
and residue field
![]() $\mathbb{F}_{q}$
, such that
$\mathbb{F}_{q}$
, such that
![]() $\bar{f}$
is nondegenerate over
$\bar{f}$
is nondegenerate over
![]() $\mathbb{F}_{q}$
with respect to the compact faces (resp. the faces) of
$\mathbb{F}_{q}$
with respect to the compact faces (resp. the faces) of
![]() $\unicode[STIX]{x1D6E4}_{0}$
. Let
$\unicode[STIX]{x1D6E4}_{0}$
. Let
![]() $\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
be a nontrivial character of conductor
$\unicode[STIX]{x1D712}:R^{\times }\rightarrow \mathbb{C}^{\times }$
be a nontrivial character of conductor
![]() $1$
. If
$1$
. If
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
) is not holomorphic on
$Z_{f}(\unicode[STIX]{x1D712},s)$
) is not holomorphic on
![]() $\mathbb{C}$
, then by the material from Section 2.3 it has a pole with real part equal to
$\mathbb{C}$
, then by the material from Section 2.3 it has a pole with real part equal to
![]() $-\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})$
for some facet
$-\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})$
for some facet
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D6E4}_{0}$
for which the order of
$\unicode[STIX]{x1D6E4}_{0}$
for which the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
divides
$\bar{\unicode[STIX]{x1D712}}$
divides
![]() $N(\unicode[STIX]{x1D70F})$
. Here, as before,
$N(\unicode[STIX]{x1D70F})$
. Here, as before,
![]() $\bar{\unicode[STIX]{x1D712}}$
denotes the unique character of
$\bar{\unicode[STIX]{x1D712}}$
denotes the unique character of
![]() $\mathbb{F}_{q}^{\times }$
associated to
$\mathbb{F}_{q}^{\times }$
associated to
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
For some facets
![]() $\unicode[STIX]{x1D70F}$
, in particular the
$\unicode[STIX]{x1D70F}$
, in particular the
![]() $B_{1}$
-facets and the
$B_{1}$
-facets and the
![]() $X_{2}$
-facets which we introduce below, we typically have to prove that
$X_{2}$
-facets which we introduce below, we typically have to prove that
![]() $-\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})$
can not be the real part of a pole of
$-\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})$
can not be the real part of a pole of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
). For the other facets, we prove that
$Z_{f}(\unicode[STIX]{x1D712},s)$
). For the other facets, we prove that
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is an eigenvalue of monodromy of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is an eigenvalue of monodromy of
![]() $f$
at some point of
$f$
at some point of
![]() $f^{-1}\{0\}$
, and we thus obtain that the order of
$f^{-1}\{0\}$
, and we thus obtain that the order of
![]() $\unicode[STIX]{x1D712}$
(which, as we recall, divides the order of
$\unicode[STIX]{x1D712}$
(which, as we recall, divides the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
) divides the order of some eigenvalue of monodromy at some point of
$\bar{\unicode[STIX]{x1D712}}$
) divides the order of some eigenvalue of monodromy at some point of
![]() $f^{-1}\{0\}$
.
$f^{-1}\{0\}$
.
Let us first recall the notion of
![]() $B_{1}$
-facets, introduced in [Reference Lemahieu and Van ProeyenLVP2]. A simplicial facet of an
$B_{1}$
-facets, introduced in [Reference Lemahieu and Van ProeyenLVP2]. A simplicial facet of an
![]() $n$
-dimensional Newton polyhedron (
$n$
-dimensional Newton polyhedron (
![]() $n\geqslant 2$
) is a
$n\geqslant 2$
) is a
![]() $B_{1}$
-simplex with respect to the variable
$B_{1}$
-simplex with respect to the variable
![]() $x_{i}$
if it is a simplex with
$x_{i}$
if it is a simplex with
![]() $n-1$
vertexes in the coordinate hyperplane
$n-1$
vertexes in the coordinate hyperplane
![]() $x_{i}=0$
and one vertex at distance 1 of this hyperplane. We say that a facet
$x_{i}=0$
and one vertex at distance 1 of this hyperplane. We say that a facet
![]() $\unicode[STIX]{x1D70F}$
of an
$\unicode[STIX]{x1D70F}$
of an
![]() $n$
-dimensional Newton polyhedron is noncompact for the variable
$n$
-dimensional Newton polyhedron is noncompact for the variable
![]() $x_{j}$
(
$x_{j}$
(
![]() $1\leqslant j\leqslant n$
) if for every point
$1\leqslant j\leqslant n$
) if for every point
![]() $p\in \unicode[STIX]{x1D70F}$
, the point
$p\in \unicode[STIX]{x1D70F}$
, the point
![]() $p+(0,\ldots ,0,1,0,\ldots ,0)\in \unicode[STIX]{x1D70F}$
, where
$p+(0,\ldots ,0,1,0,\ldots ,0)\in \unicode[STIX]{x1D70F}$
, where
![]() $(0,\ldots ,0,1,0,\ldots ,0)$
is an
$(0,\ldots ,0,1,0,\ldots ,0)$
is an
![]() $n$
-tuple with 1 at place
$n$
-tuple with 1 at place
![]() $j$
and 0 everywhere else. We define the maps
$j$
and 0 everywhere else. We define the maps
A noncompact facet
![]() $\unicode[STIX]{x1D70F}$
of an
$\unicode[STIX]{x1D70F}$
of an
![]() $n$
-dimensional Newton polyhedron (
$n$
-dimensional Newton polyhedron (
![]() $n\geqslant 3$
) is a (noncompact)
$n\geqslant 3$
) is a (noncompact)
![]() $B_{1}$
-facet with respect to the variable
$B_{1}$
-facet with respect to the variable
![]() $x_{i}$
if
$x_{i}$
if
![]() $\unicode[STIX]{x1D70F}$
is noncompact for exactly one variable
$\unicode[STIX]{x1D70F}$
is noncompact for exactly one variable
![]() $x_{j}$
and if
$x_{j}$
and if
![]() $\unicode[STIX]{x1D70B}_{j}(\unicode[STIX]{x1D70F})$
is a
$\unicode[STIX]{x1D70B}_{j}(\unicode[STIX]{x1D70F})$
is a
![]() $B_{1}$
-simplex in
$B_{1}$
-simplex in
![]() $\mathbb{R}^{n-1}$
with respect to
$\mathbb{R}^{n-1}$
with respect to
![]() $x_{i}$
. A
$x_{i}$
. A
![]() $B_{1}$
-facet is a
$B_{1}$
-facet is a
![]() $B_{1}$
-simplex or a noncompact
$B_{1}$
-simplex or a noncompact
![]() $B_{1}$
-facet with respect to some variable.
$B_{1}$
-facet with respect to some variable.
Here, in addition, we introduce the following.
Definition 11. A facet of type
![]() $X_{2}$
in a
$X_{2}$
in a
![]() $3$
-dimensional Newton polyhedron is a facet whose vertexes (up to permutation of the coordinates) are of the form
$3$
-dimensional Newton polyhedron is a facet whose vertexes (up to permutation of the coordinates) are of the form
![]() $p=(a,0,0),q=(x_{1},0,2)$
,
$p=(a,0,0),q=(x_{1},0,2)$
,
![]() $r=(x_{2},2,0)$
, with
$r=(x_{2},2,0)$
, with
![]() $a-x_{2}$
and
$a-x_{2}$
and
![]() $a-x_{1}$
both odd.
$a-x_{1}$
both odd.
Remark that an
![]() $X_{2}$
-facet has four lattice points: besides its three vertexes, we have the point
$X_{2}$
-facet has four lattice points: besides its three vertexes, we have the point
![]() $((x_{1}+x_{2})/2,1,1)$
. Also notice that a simplex cannot be simultaneously
$((x_{1}+x_{2})/2,1,1)$
. Also notice that a simplex cannot be simultaneously
![]() $B_{1}$
and
$B_{1}$
and
![]() $X_{2}$
, except when it is spanned by
$X_{2}$
, except when it is spanned by
![]() $(1,0,0)$
,
$(1,0,0)$
,
![]() $(0,0,2)$
,
$(0,0,2)$
,
![]() $(0,2,0)$
(up to permutation of the coordinates); that is, it is the only compact facet of
$(0,2,0)$
(up to permutation of the coordinates); that is, it is the only compact facet of
![]() $\unicode[STIX]{x1D6E4}_{0}$
. By Lemma 14 below, this facet does not give rise to an actual pole of
$\unicode[STIX]{x1D6E4}_{0}$
. By Lemma 14 below, this facet does not give rise to an actual pole of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
or
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
or
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
.
$Z_{f}(\unicode[STIX]{x1D712},s)$
.
5.1 Determination of a set of eigenvalues
As in Section 2.4, we subdivide the compact facets of
![]() $\unicode[STIX]{x1D6E4}_{0}$
into simplices
$\unicode[STIX]{x1D6E4}_{0}$
into simplices
![]() $\unicode[STIX]{x1D70F}$
. In [Reference Lemahieu and Van ProeyenLVP2, Proposition 8], Van Proeyen and Lemahieu proved that whenever
$\unicode[STIX]{x1D70F}$
. In [Reference Lemahieu and Van ProeyenLVP2, Proposition 8], Van Proeyen and Lemahieu proved that whenever
![]() $\unicode[STIX]{x1D70F}$
is not a
$\unicode[STIX]{x1D70F}$
is not a
![]() $B_{1}$
-facet, then the value
$B_{1}$
-facet, then the value
![]() $e^{-2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})}$
is a root of
$e^{-2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})}$
is a root of
![]() $F_{\unicode[STIX]{x1D70F}}$
. In this section, we show that
$F_{\unicode[STIX]{x1D70F}}$
. In this section, we show that
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is also a root of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is also a root of
![]() $F_{\unicode[STIX]{x1D70F}}$
, except possibly if
$F_{\unicode[STIX]{x1D70F}}$
, except possibly if
![]() $\unicode[STIX]{x1D70F}$
is a
$\unicode[STIX]{x1D70F}$
is a
![]() $B_{1}$
-facet or an
$B_{1}$
-facet or an
![]() $X_{2}$
-facet. Contrary to [Reference Lemahieu and Van ProeyenLVP2, Proposition 8], we here rely on Proposition 5 to get a more conceptual proof.
$X_{2}$
-facet. Contrary to [Reference Lemahieu and Van ProeyenLVP2, Proposition 8], we here rely on Proposition 5 to get a more conceptual proof.
Proposition 12. Let
![]() $\unicode[STIX]{x1D70F}$
be a simplex in a subdivision of a compact facet of some 3-dimensional Newton polyhedron. Suppose that
$\unicode[STIX]{x1D70F}$
be a simplex in a subdivision of a compact facet of some 3-dimensional Newton polyhedron. Suppose that
![]() $\unicode[STIX]{x1D70F}$
is not of type
$\unicode[STIX]{x1D70F}$
is not of type
![]() $B_{1}$
or of type
$B_{1}$
or of type
![]() $X_{2}$
, then
$X_{2}$
, then
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
![]() $F_{\unicode[STIX]{x1D70F}}$
.
$F_{\unicode[STIX]{x1D70F}}$
.
Proof.
Case 1.
![]() $\unicode[STIX]{x1D70F}$
does not contain a segment in a coordinate plane.
$\unicode[STIX]{x1D70F}$
does not contain a segment in a coordinate plane.
By formula (2),
![]() $F_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70F}}=\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70F})}$
, and
$F_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70F}}=\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70F})}$
, and
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
clearly is a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
clearly is a zero of
![]() $F_{\unicode[STIX]{x1D70F}}$
.
$F_{\unicode[STIX]{x1D70F}}$
.
Case 2.
![]() $\unicode[STIX]{x1D70F}$
contains exactly one
$\unicode[STIX]{x1D70F}$
contains exactly one
![]() $1$
-dimensional V-face
$1$
-dimensional V-face
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
In this case, we have
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D70F}}=\frac{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}}}=\frac{\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70F})}}{\left(1-t^{N(\unicode[STIX]{x1D70E})}\right)^{\text{NV}(\unicode[STIX]{x1D70E})}}.\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D70F}}=\frac{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}}}=\frac{\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70F})}}{\left(1-t^{N(\unicode[STIX]{x1D70E})}\right)^{\text{NV}(\unicode[STIX]{x1D70E})}}.\end{eqnarray}$$
Then,
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
![]() $F_{\unicode[STIX]{x1D70F}}$
unless
$F_{\unicode[STIX]{x1D70F}}$
unless
![]() $N(\unicode[STIX]{x1D70E})=N(\unicode[STIX]{x1D70F})$
and
$N(\unicode[STIX]{x1D70E})=N(\unicode[STIX]{x1D70F})$
and
![]() $\text{NV}(\unicode[STIX]{x1D70E})=\text{NV}(\unicode[STIX]{x1D70F})$
. One easily checks that then
$\text{NV}(\unicode[STIX]{x1D70E})=\text{NV}(\unicode[STIX]{x1D70F})$
. One easily checks that then
![]() $\unicode[STIX]{x1D70F}$
would be a
$\unicode[STIX]{x1D70F}$
would be a
![]() $B_{1}$
-facet.
$B_{1}$
-facet.
Case 3.
![]() $\unicode[STIX]{x1D70F}$
contains exactly two
$\unicode[STIX]{x1D70F}$
contains exactly two
![]() $1$
-dimensional V-faces
$1$
-dimensional V-faces
![]() $\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
.
$\unicode[STIX]{x1D70E}_{2}$
.
In this situation,
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D70F}}=\frac{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}_{p}}{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}_{1}}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}_{2}}}=\frac{(1-t^{l})\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70F})}}{\left(1-t^{N(\unicode[STIX]{x1D70E}_{1})}\right)^{\text{NV}(\unicode[STIX]{x1D70E}_{1})}\left(1-t^{N(\unicode[STIX]{x1D70E}_{2})}\right)^{\text{NV}(\unicode[STIX]{x1D70E}_{2})}},\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D70F}}=\frac{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}_{p}}{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}_{1}}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D70E}_{2}}}=\frac{(1-t^{l})\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70F})}}{\left(1-t^{N(\unicode[STIX]{x1D70E}_{1})}\right)^{\text{NV}(\unicode[STIX]{x1D70E}_{1})}\left(1-t^{N(\unicode[STIX]{x1D70E}_{2})}\right)^{\text{NV}(\unicode[STIX]{x1D70E}_{2})}},\end{eqnarray}$$
where, without loss of generality,
![]() $\left\{p=\left(l,0,0\right)\right\}=\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2}$
.
$\left\{p=\left(l,0,0\right)\right\}=\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2}$
.
If
![]() $N(\unicode[STIX]{x1D70E}_{1})\neq N(\unicode[STIX]{x1D70F})$
or
$N(\unicode[STIX]{x1D70E}_{1})\neq N(\unicode[STIX]{x1D70F})$
or
![]() $N(\unicode[STIX]{x1D70E}_{2})\neq N(\unicode[STIX]{x1D70F})$
, then see Cases 1 and 2. If
$N(\unicode[STIX]{x1D70E}_{2})\neq N(\unicode[STIX]{x1D70F})$
, then see Cases 1 and 2. If
![]() $N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})$
, then
$N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})$
, then
![]() $F_{\unicode[STIX]{x1D70F}}=(1-t^{l})\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70F})-\text{NV}(\unicode[STIX]{x1D70E}_{1})-\text{NV}(\unicode[STIX]{x1D70E}_{2})}$
.
$F_{\unicode[STIX]{x1D70F}}=(1-t^{l})\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70F})-\text{NV}(\unicode[STIX]{x1D70E}_{1})-\text{NV}(\unicode[STIX]{x1D70E}_{2})}$
.
Case 3.1. If
![]() $N(p)=N(\unicode[STIX]{x1D70F})$
, then by Proposition 5,
$N(p)=N(\unicode[STIX]{x1D70F})$
, then by Proposition 5,
![]() $\text{NV}(\unicode[STIX]{x1D70F})=\text{NV}(\unicode[STIX]{x1D70E}_{1})\text{NV}(\unicode[STIX]{x1D70E}_{2})$
and hence
$\text{NV}(\unicode[STIX]{x1D70F})=\text{NV}(\unicode[STIX]{x1D70E}_{1})\text{NV}(\unicode[STIX]{x1D70E}_{2})$
and hence
![]() $F_{\unicode[STIX]{x1D70F}}=\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\left(\text{NV}(\unicode[STIX]{x1D70E}_{1})-1\right)\left(\text{NV}(\unicode[STIX]{x1D70E}_{2})-1\right)}$
. If
$F_{\unicode[STIX]{x1D70F}}=\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\left(\text{NV}(\unicode[STIX]{x1D70E}_{1})-1\right)\left(\text{NV}(\unicode[STIX]{x1D70E}_{2})-1\right)}$
. If
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})$
or
$\text{NV}(\unicode[STIX]{x1D70E}_{1})$
or
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{2})$
would be equal to
$\text{NV}(\unicode[STIX]{x1D70E}_{2})$
would be equal to
![]() $1$
, then it would result that
$1$
, then it would result that
![]() $\text{NV}(\unicode[STIX]{x1D70F})=\text{NV}(\unicode[STIX]{x1D70E}_{i})$
, for some
$\text{NV}(\unicode[STIX]{x1D70F})=\text{NV}(\unicode[STIX]{x1D70E}_{i})$
, for some
![]() $i\in \{1,2\}$
, and again
$i\in \{1,2\}$
, and again
![]() $\unicode[STIX]{x1D70F}$
would be a
$\unicode[STIX]{x1D70F}$
would be a
![]() $B_{1}$
-facet. Consequently,
$B_{1}$
-facet. Consequently,
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
![]() $F_{\unicode[STIX]{x1D70F}}$
.
$F_{\unicode[STIX]{x1D70F}}$
.
Case 3.2. Suppose that
![]() $N(p)\neq N(\unicode[STIX]{x1D70F})$
. By Proposition 5, we have
$N(p)\neq N(\unicode[STIX]{x1D70F})$
. By Proposition 5, we have
![]() $\text{NV}(\unicode[STIX]{x1D70F})=M\text{NV}(\unicode[STIX]{x1D70E}_{1})\text{NV}(\unicode[STIX]{x1D70E}_{2})$
, with
$\text{NV}(\unicode[STIX]{x1D70F})=M\text{NV}(\unicode[STIX]{x1D70E}_{1})\text{NV}(\unicode[STIX]{x1D70E}_{2})$
, with
![]() $M\geqslant 2$
. One easily deduces that
$M\geqslant 2$
. One easily deduces that
![]() $\text{NV}(\unicode[STIX]{x1D70F})-\text{NV}(\unicode[STIX]{x1D70E}_{1})-\text{NV}(\unicode[STIX]{x1D70E}_{2})>0$
, unless
$\text{NV}(\unicode[STIX]{x1D70F})-\text{NV}(\unicode[STIX]{x1D70E}_{1})-\text{NV}(\unicode[STIX]{x1D70E}_{2})>0$
, unless
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})=\text{NV}(\unicode[STIX]{x1D70E}_{2})=1$
. If
$\text{NV}(\unicode[STIX]{x1D70E}_{1})=\text{NV}(\unicode[STIX]{x1D70E}_{2})=1$
. If
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})=\text{NV}(\unicode[STIX]{x1D70E}_{2})=1$
, then
$\text{NV}(\unicode[STIX]{x1D70E}_{1})=\text{NV}(\unicode[STIX]{x1D70E}_{2})=1$
, then
![]() $\text{NV}(\unicode[STIX]{x1D70F})-\text{NV}(\unicode[STIX]{x1D70E}_{1})-\text{NV}(\unicode[STIX]{x1D70E}_{2})>0$
if and only if
$\text{NV}(\unicode[STIX]{x1D70F})-\text{NV}(\unicode[STIX]{x1D70E}_{1})-\text{NV}(\unicode[STIX]{x1D70E}_{2})>0$
if and only if
![]() $M>2$
. It remains thus to study the case
$M>2$
. It remains thus to study the case
![]() $\text{NV}(\unicode[STIX]{x1D70F})=M=2$
,
$\text{NV}(\unicode[STIX]{x1D70F})=M=2$
,
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})=\text{NV}(\unicode[STIX]{x1D70E}_{2})=1$
. As we supposed that
$\text{NV}(\unicode[STIX]{x1D70E}_{1})=\text{NV}(\unicode[STIX]{x1D70E}_{2})=1$
. As we supposed that
![]() $N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})$
, the vertexes of
$N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})$
, the vertexes of
![]() $\unicode[STIX]{x1D70F}$
are then
$\unicode[STIX]{x1D70F}$
are then
![]() $p=(N(\unicode[STIX]{x1D70F})/2,0,0),q=(x_{1},0,2),r=(x_{2},2,0)$
, and
$p=(N(\unicode[STIX]{x1D70F})/2,0,0),q=(x_{1},0,2),r=(x_{2},2,0)$
, and
From
![]() $N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70F})$
, it follows that
$N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70F})$
, it follows that
![]() $N(\unicode[STIX]{x1D70F})/2-x_{2}$
and
$N(\unicode[STIX]{x1D70F})/2-x_{2}$
and
![]() $N(\unicode[STIX]{x1D70F})/2-x_{1}$
are odd, and hence
$N(\unicode[STIX]{x1D70F})/2-x_{1}$
are odd, and hence
![]() $\unicode[STIX]{x1D70F}$
is of type
$\unicode[STIX]{x1D70F}$
is of type
![]() $X_{2}$
.
$X_{2}$
.
Case 4.
![]() $\unicode[STIX]{x1D70F}$
contains three
$\unicode[STIX]{x1D70F}$
contains three
![]() $1$
-dimensional V-faces
$1$
-dimensional V-faces
![]() $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}$
and
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}$
and
![]() $\unicode[STIX]{x1D70E}_{3}$
.
$\unicode[STIX]{x1D70E}_{3}$
.
In this situation,
with
![]() $p=\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2}$
,
$p=\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2}$
,
![]() $q=\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3}$
and
$q=\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3}$
and
![]() $r=\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3}$
. We suppose that
$r=\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3}$
. We suppose that
![]() $N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70E}_{3})$
; if not, then we fall back on one of the previous cases.
$N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70E}_{3})$
; if not, then we fall back on one of the previous cases.
Case 4.1. If
![]() $N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3})=N(\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3})$
, then, by Proposition 5,
$N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3})=N(\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3})$
, then, by Proposition 5,
![]() $\text{NV}(\unicode[STIX]{x1D70F})=\text{NV}(\unicode[STIX]{x1D70E}_{1})\text{NV}(\unicode[STIX]{x1D70E}_{2})=\text{NV}(\unicode[STIX]{x1D70E}_{1})\text{NV}(\unicode[STIX]{x1D70E}_{3})=\text{NV}(\unicode[STIX]{x1D70E}_{2})\text{NV}(\unicode[STIX]{x1D70E}_{3})$
, and thus
$\text{NV}(\unicode[STIX]{x1D70F})=\text{NV}(\unicode[STIX]{x1D70E}_{1})\text{NV}(\unicode[STIX]{x1D70E}_{2})=\text{NV}(\unicode[STIX]{x1D70E}_{1})\text{NV}(\unicode[STIX]{x1D70E}_{3})=\text{NV}(\unicode[STIX]{x1D70E}_{2})\text{NV}(\unicode[STIX]{x1D70E}_{3})$
, and thus
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})=\text{NV}(\unicode[STIX]{x1D70E}_{2})=\text{NV}(\unicode[STIX]{x1D70E}_{3})$
. Then,
$\text{NV}(\unicode[STIX]{x1D70E}_{1})=\text{NV}(\unicode[STIX]{x1D70E}_{2})=\text{NV}(\unicode[STIX]{x1D70E}_{3})$
. Then,
![]() $F_{\unicode[STIX]{x1D70F}}$
becomes
$F_{\unicode[STIX]{x1D70F}}$
becomes
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D70F}}=\frac{\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70E}_{1})^{2}+3}}{\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{3\text{NV}(\unicode[STIX]{x1D70E}_{1})}}.\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D70F}}=\frac{\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{\text{NV}(\unicode[STIX]{x1D70E}_{1})^{2}+3}}{\left(1-t^{N(\unicode[STIX]{x1D70F})}\right)^{3\text{NV}(\unicode[STIX]{x1D70E}_{1})}}.\end{eqnarray}$$
Since
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})^{2}+3>3\text{NV}(\unicode[STIX]{x1D70E}_{1})$
, it follows that
$\text{NV}(\unicode[STIX]{x1D70E}_{1})^{2}+3>3\text{NV}(\unicode[STIX]{x1D70E}_{1})$
, it follows that
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
![]() $F_{\unicode[STIX]{x1D70F}}$
.
$F_{\unicode[STIX]{x1D70F}}$
.
Case 4.2. If
![]() $N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3})\neq N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3})$
, then Proposition 5 yields
$N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3})\neq N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3})$
, then Proposition 5 yields
We thus get
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{3})=\text{NV}(\unicode[STIX]{x1D70E}_{1})$
and
$\text{NV}(\unicode[STIX]{x1D70E}_{3})=\text{NV}(\unicode[STIX]{x1D70E}_{1})$
and
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{2})=M\text{NV}(\unicode[STIX]{x1D70E}_{1})$
, and we find then
$\text{NV}(\unicode[STIX]{x1D70E}_{2})=M\text{NV}(\unicode[STIX]{x1D70E}_{1})$
, and we find then
with
![]() $p=(N(\unicode[STIX]{x1D70F}),0,0),q=(0,N(\unicode[STIX]{x1D70F})/M,0)$
and
$p=(N(\unicode[STIX]{x1D70F}),0,0),q=(0,N(\unicode[STIX]{x1D70F})/M,0)$
and
![]() $r=(0,0,N(\unicode[STIX]{x1D70F}))$
. In this case,
$r=(0,0,N(\unicode[STIX]{x1D70F}))$
. In this case,
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
![]() $F_{\unicode[STIX]{x1D70F}}$
if and only if
$F_{\unicode[STIX]{x1D70F}}$
if and only if
![]() $\text{NV}(\unicode[STIX]{x1D70F})+2>\text{NV}(\unicode[STIX]{x1D70E}_{1})+\text{NV}(\unicode[STIX]{x1D70E}_{2})+\text{NV}(\unicode[STIX]{x1D70E}_{3})$
, or, equivalently, if
$\text{NV}(\unicode[STIX]{x1D70F})+2>\text{NV}(\unicode[STIX]{x1D70E}_{1})+\text{NV}(\unicode[STIX]{x1D70E}_{2})+\text{NV}(\unicode[STIX]{x1D70E}_{3})$
, or, equivalently, if
![]() $\left(M\text{NV}(\unicode[STIX]{x1D70E}_{1})-2\right)\left(\text{NV}(\unicode[STIX]{x1D70E}_{1})-1\right)>0$
. This is always the case, as
$\left(M\text{NV}(\unicode[STIX]{x1D70E}_{1})-2\right)\left(\text{NV}(\unicode[STIX]{x1D70E}_{1})-1\right)>0$
. This is always the case, as
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70F})/M=1$
would imply that
$\text{NV}(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70F})/M=1$
would imply that
![]() $\unicode[STIX]{x1D70F}$
is a
$\unicode[STIX]{x1D70F}$
is a
![]() $B_{1}$
-facet.
$B_{1}$
-facet.
Case 4.3. If
![]() $N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2})$
,
$N(\unicode[STIX]{x1D70F})=N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2})$
,
![]() $N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3})$
and
$N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3})$
and
![]() $N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3})$
, then, by Proposition 5, one has
$N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3})$
, then, by Proposition 5, one has
with
![]() $M_{1}\geqslant 2$
and
$M_{1}\geqslant 2$
and
![]() $M_{2}\geqslant 2$
. In this configuration, we have
$M_{2}\geqslant 2$
. In this configuration, we have
![]() $p=(N(\unicode[STIX]{x1D70F}),0,0),q=(0,N(\unicode[STIX]{x1D70F})/k,0)$
and
$p=(N(\unicode[STIX]{x1D70F}),0,0),q=(0,N(\unicode[STIX]{x1D70F})/k,0)$
and
![]() $r=(0,0,N(\unicode[STIX]{x1D70F})/l)$
, with
$r=(0,0,N(\unicode[STIX]{x1D70F})/l)$
, with
![]() $\gcd (k,l)=1$
. Then, we find that
$\gcd (k,l)=1$
. Then, we find that
![]() $M_{1}=k$
,
$M_{1}=k$
,
![]() $M_{2}=l$
, and hence
$M_{2}=l$
, and hence
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{2})=k\text{NV}(\unicode[STIX]{x1D70E}_{1})/l$
and
$\text{NV}(\unicode[STIX]{x1D70E}_{2})=k\text{NV}(\unicode[STIX]{x1D70E}_{1})/l$
and
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{3})=\text{NV}(\unicode[STIX]{x1D70E}_{1})/l$
. In this case,
$\text{NV}(\unicode[STIX]{x1D70E}_{3})=\text{NV}(\unicode[STIX]{x1D70E}_{1})/l$
. In this case,
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
would be a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
would be a zero of
![]() $F_{\unicode[STIX]{x1D70F}}$
if and only if
$F_{\unicode[STIX]{x1D70F}}$
if and only if
![]() $\text{NV}(\unicode[STIX]{x1D70F})+1>\text{NV}(\unicode[STIX]{x1D70E}_{1})+\text{NV}(\unicode[STIX]{x1D70E}_{2})+\text{NV}(\unicode[STIX]{x1D70E}_{3})$
, or, equivalently,
$\text{NV}(\unicode[STIX]{x1D70F})+1>\text{NV}(\unicode[STIX]{x1D70E}_{1})+\text{NV}(\unicode[STIX]{x1D70E}_{2})+\text{NV}(\unicode[STIX]{x1D70E}_{3})$
, or, equivalently,
This is true because
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})\geqslant l$
, while the largest real root of the polynomial on the left-hand side is
$\text{NV}(\unicode[STIX]{x1D70E}_{1})\geqslant l$
, while the largest real root of the polynomial on the left-hand side is
The latter inequality holds because one easily rewrites it as
![]() $kl>k+l$
, which holds since
$kl>k+l$
, which holds since
![]() $k,l\geqslant 2$
, and
$k,l\geqslant 2$
, and
![]() $k=l=2$
is excluded by coprimality.
$k=l=2$
is excluded by coprimality.
Case 4.4. If
![]() $N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2})$
,
$N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{2})$
,
![]() $N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3})$
and
$N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{1}\cap \unicode[STIX]{x1D70E}_{3})$
and
![]() $N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3})$
, then, by Proposition 5, one has
$N(\unicode[STIX]{x1D70F})\neq N(\unicode[STIX]{x1D70E}_{2}\cap \unicode[STIX]{x1D70E}_{3})$
, then, by Proposition 5, one has
with
![]() $M_{1}\geqslant 2$
,
$M_{1}\geqslant 2$
,
![]() $M_{2}\geqslant 2$
and
$M_{2}\geqslant 2$
and
![]() $M_{3}\geqslant 2$
. In this configuration, we have
$M_{3}\geqslant 2$
. In this configuration, we have
![]() $p=(N(\unicode[STIX]{x1D70F})/k,0,0),q=(0,N(\unicode[STIX]{x1D70F})/l,0)$
and
$p=(N(\unicode[STIX]{x1D70F})/k,0,0),q=(0,N(\unicode[STIX]{x1D70F})/l,0)$
and
![]() $r=(0,0,N(\unicode[STIX]{x1D70F})/m)$
, with
$r=(0,0,N(\unicode[STIX]{x1D70F})/m)$
, with
![]() $k,l,m$
pairwise coprime. Then, we find that
$k,l,m$
pairwise coprime. Then, we find that
![]() $M_{1}=k$
,
$M_{1}=k$
,
![]() $M_{2}=l$
,
$M_{2}=l$
,
![]() $M_{3}=m$
, and hence
$M_{3}=m$
, and hence
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{2})=l\text{NV}(\unicode[STIX]{x1D70E}_{1})/m$
and
$\text{NV}(\unicode[STIX]{x1D70E}_{2})=l\text{NV}(\unicode[STIX]{x1D70E}_{1})/m$
and
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{3})=k\text{NV}(\unicode[STIX]{x1D70E}_{1})/m$
. In this case, we want to establish that
$\text{NV}(\unicode[STIX]{x1D70E}_{3})=k\text{NV}(\unicode[STIX]{x1D70E}_{1})/m$
. In this case, we want to establish that
![]() $\text{NV}(\unicode[STIX]{x1D70F})>\text{NV}(\unicode[STIX]{x1D70E}_{1})+\text{NV}(\unicode[STIX]{x1D70E}_{2})+\text{NV}(\unicode[STIX]{x1D70E}_{3})$
, or equivalently that
$\text{NV}(\unicode[STIX]{x1D70F})>\text{NV}(\unicode[STIX]{x1D70E}_{1})+\text{NV}(\unicode[STIX]{x1D70E}_{2})+\text{NV}(\unicode[STIX]{x1D70E}_{3})$
, or equivalently that
![]() $klm\text{NV}(\unicode[STIX]{x1D70E}_{1})>k+l+m$
. This follows from
$klm\text{NV}(\unicode[STIX]{x1D70E}_{1})>k+l+m$
. This follows from
![]() $\text{NV}(\unicode[STIX]{x1D70E}_{1})\geqslant 1$
and
$\text{NV}(\unicode[STIX]{x1D70E}_{1})\geqslant 1$
and
![]() $klm\geqslant 4\max \{k,l,m\}>3\max \{k,l,m\}\geqslant k+l+m$
.◻
$klm\geqslant 4\max \{k,l,m\}>3\max \{k,l,m\}\geqslant k+l+m$
.◻
The above result reduces our analysis to the study of compact facets of
![]() $\unicode[STIX]{x1D6E4}_{0}$
, all of whose subdivisions into simplices consist purely of
$\unicode[STIX]{x1D6E4}_{0}$
, all of whose subdivisions into simplices consist purely of
![]() $B_{1}$
-facets or
$B_{1}$
-facets or
![]() $X_{2}$
-facets. In fact, these types cannot appear within the same such facet of
$X_{2}$
-facets. In fact, these types cannot appear within the same such facet of
![]() $\unicode[STIX]{x1D6E4}_{0}$
, because one easily verifies that a
$\unicode[STIX]{x1D6E4}_{0}$
, because one easily verifies that a
![]() $B_{1}$
-facet and an
$B_{1}$
-facet and an
![]() $X_{2}$
-facet can never share an edge.
$X_{2}$
-facet can never share an edge.
For now, we restrict our attention to simplicial facets of
![]() $\unicode[STIX]{x1D6E4}_{0}$
that are of type
$\unicode[STIX]{x1D6E4}_{0}$
that are of type
![]() $B_{1}$
or
$B_{1}$
or
![]() $X_{2}$
. More precisely, in the next section, we prove the fakeness of most candidate poles contributed by such facets. Notice that if two facets only have a vertex in common, then one can subdivide the cone dual to that vertex in such a way that the contributions of these facets to the Igusa zeta function can be analyzed separately. This reduces our analysis to ‘clusters’ or ‘configurations’ of
$X_{2}$
. More precisely, in the next section, we prove the fakeness of most candidate poles contributed by such facets. Notice that if two facets only have a vertex in common, then one can subdivide the cone dual to that vertex in such a way that the contributions of these facets to the Igusa zeta function can be analyzed separately. This reduces our analysis to ‘clusters’ or ‘configurations’ of
![]() $B_{1}$
-facets or
$B_{1}$
-facets or
![]() $X_{2}$
-facets contributing the same candidate pole, by which we mean a collection of facets of which each member has at least one edge in common with another member.
$X_{2}$
-facets contributing the same candidate pole, by which we mean a collection of facets of which each member has at least one edge in common with another member.
5.2 On false poles
5.2.1 Preliminary facts
We first make the following observations, which hold up to permutation of the coordinates.
Fact 1. A vertex
![]() $P=(1,\cdot ,\cdot )$
does not contribute. Indeed, as
$P=(1,\cdot ,\cdot )$
does not contribute. Indeed, as
![]() $\unicode[STIX]{x1D712}$
is not the trivial character (and so neither is
$\unicode[STIX]{x1D712}$
is not the trivial character (and so neither is
![]() $\bar{\unicode[STIX]{x1D712}}$
trivial), one immediately deduces from Lemma 8 that the contribution of
$\bar{\unicode[STIX]{x1D712}}$
trivial), one immediately deduces from Lemma 8 that the contribution of
![]() $P$
is equal to
$P$
is equal to
![]() $0$
.
$0$
.
Fact 2. A vertex
![]() $P=(a,0,0)$
does not contribute if the order of
$P=(a,0,0)$
does not contribute if the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
$\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
![]() $a$
(again by Lemma 8).
$a$
(again by Lemma 8).
Fact 3. A segment
![]() $\unicode[STIX]{x1D70E}:=PQ$
with
$\unicode[STIX]{x1D70E}:=PQ$
with
![]() $P=(1,1,b)$
and
$P=(1,1,b)$
and
![]() $Q=(0,0,a)$
does not contribute if the order of
$Q=(0,0,a)$
does not contribute if the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
$\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
![]() $a$
. To compute the contribution of
$a$
. To compute the contribution of
![]() $\unicode[STIX]{x1D70E}$
, we consider
$\unicode[STIX]{x1D70E}$
, we consider
By using Lemma 9, this expression simplifies to
If the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
$\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
![]() $a$
, then it follows from Lemma 8 that the contribution of
$a$
, then it follows from Lemma 8 that the contribution of
![]() $\unicode[STIX]{x1D70E}$
is equal to
$\unicode[STIX]{x1D70E}$
is equal to
![]() $0$
.
$0$
.
Fact 4. Let
![]() $\unicode[STIX]{x1D70E}:=PQ$
, with
$\unicode[STIX]{x1D70E}:=PQ$
, with
![]() $P=(\cdot ,\cdot ,0)$
and
$P=(\cdot ,\cdot ,0)$
and
![]() $Q=(\cdot ,\cdot ,0)$
, and let
$Q=(\cdot ,\cdot ,0)$
, and let
![]() $\unicode[STIX]{x1D70F}:=PQR$
with
$\unicode[STIX]{x1D70F}:=PQR$
with
![]() $R=(\cdot ,\cdot ,1)$
be the facet not contained in
$R=(\cdot ,\cdot ,1)$
be the facet not contained in
![]() $\{z=0\}$
that contains
$\{z=0\}$
that contains
![]() $\unicode[STIX]{x1D70E}$
, then
$\unicode[STIX]{x1D70E}$
, then
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70F}$
cancel each other out. Indeed, by Lemma 9 with
$\unicode[STIX]{x1D70F}$
cancel each other out. Indeed, by Lemma 9 with
![]() $f=f_{\unicode[STIX]{x1D70E}}$
, it follows that
$f=f_{\unicode[STIX]{x1D70E}}$
, it follows that
![]() $L_{\unicode[STIX]{x1D70E}}=(1-q)L_{\unicode[STIX]{x1D70F}}$
. As mult
$L_{\unicode[STIX]{x1D70E}}=(1-q)L_{\unicode[STIX]{x1D70F}}$
. As mult
![]() $(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}})=1$
, we find that
$(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}})=1$
, we find that
![]() $L_{\unicode[STIX]{x1D70E}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}})+L_{\unicode[STIX]{x1D70F}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})=0$
.
$L_{\unicode[STIX]{x1D70E}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}})+L_{\unicode[STIX]{x1D70F}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})=0$
.
Fact 5. Let
![]() $\unicode[STIX]{x1D70E}:=PQ$
, with
$\unicode[STIX]{x1D70E}:=PQ$
, with
![]() $P=(\cdot ,\cdot ,0)$
and
$P=(\cdot ,\cdot ,0)$
and
![]() $Q=(\cdot ,\cdot ,1)$
, then, again by Lemma 9, one finds
$Q=(\cdot ,\cdot ,1)$
, then, again by Lemma 9, one finds
![]() $L_{P}=(1-q)L_{\unicode[STIX]{x1D70E}}$
. Now, let
$L_{P}=(1-q)L_{\unicode[STIX]{x1D70E}}$
. Now, let
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70F}_{2}$
be the facets containing
$\unicode[STIX]{x1D70F}_{2}$
be the facets containing
![]() $\unicode[STIX]{x1D70E}$
, and let
$\unicode[STIX]{x1D70E}$
, and let
![]() $\unicode[STIX]{x1D70F}_{0}$
be the facet in
$\unicode[STIX]{x1D70F}_{0}$
be the facet in
![]() $\{z=0\}$
containing the vertex
$\{z=0\}$
containing the vertex
![]() $P$
. With
$P$
. With
![]() $\unicode[STIX]{x1D6FF}_{P}$
the cone (strictly positively) spanned by
$\unicode[STIX]{x1D6FF}_{P}$
the cone (strictly positively) spanned by
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}_{0}},\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}_{1}}$
and
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}_{0}},\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}_{1}}$
and
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}_{2}}$
, we then find that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}_{2}}$
, we then find that
![]() $L_{\unicode[STIX]{x1D70E}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}})+L_{P}S(\unicode[STIX]{x1D6FF}_{P})=0$
.
$L_{\unicode[STIX]{x1D70E}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}})+L_{P}S(\unicode[STIX]{x1D6FF}_{P})=0$
.
Fact 6. Let
![]() $\unicode[STIX]{x1D70E}:=PQ$
, with
$\unicode[STIX]{x1D70E}:=PQ$
, with
![]() $P=(\cdot ,\cdot ,0)$
and
$P=(\cdot ,\cdot ,0)$
and
![]() $Q=(\cdot ,\cdot ,1)$
, and let
$Q=(\cdot ,\cdot ,1)$
, and let
![]() $\unicode[STIX]{x1D70F}_{1}$
be a noncompact
$\unicode[STIX]{x1D70F}_{1}$
be a noncompact
![]() $B_{1}$
-facet containing
$B_{1}$
-facet containing
![]() $\unicode[STIX]{x1D70E}$
. Let
$\unicode[STIX]{x1D70E}$
. Let
![]() $\unicode[STIX]{x1D70F}_{2}$
be the noncompact facet containing the vertex
$\unicode[STIX]{x1D70F}_{2}$
be the noncompact facet containing the vertex
![]() $Q$
and sharing a half line with
$Q$
and sharing a half line with
![]() $\unicode[STIX]{x1D70F}_{1}$
. Lemma 8 implies that
$\unicode[STIX]{x1D70F}_{1}$
. Lemma 8 implies that
![]() $\unicode[STIX]{x1D70F}_{1}\cap \unicode[STIX]{x1D70F}_{2}$
does not contribute in the formula for
$\unicode[STIX]{x1D70F}_{1}\cap \unicode[STIX]{x1D70F}_{2}$
does not contribute in the formula for
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
.
$Z_{f}(\unicode[STIX]{x1D712},s)$
.
Fact 7. Let
![]() $\unicode[STIX]{x1D70E}:=PQ$
, with
$\unicode[STIX]{x1D70E}:=PQ$
, with
![]() $P=(\cdot ,\cdot ,0)$
and
$P=(\cdot ,\cdot ,0)$
and
![]() $Q=(\cdot ,\cdot ,1)$
, and let
$Q=(\cdot ,\cdot ,1)$
, and let
![]() $\unicode[STIX]{x1D70F}_{1}$
be a noncompact
$\unicode[STIX]{x1D70F}_{1}$
be a noncompact
![]() $B_{1}$
-facet containing
$B_{1}$
-facet containing
![]() $\unicode[STIX]{x1D70E}$
. Let
$\unicode[STIX]{x1D70E}$
. Let
![]() $\unicode[STIX]{x1D70F}_{0}$
be the noncompact facet containing the vertex
$\unicode[STIX]{x1D70F}_{0}$
be the noncompact facet containing the vertex
![]() $P$
and sharing a half line
$P$
and sharing a half line
![]() $\unicode[STIX]{x1D70E}_{1}$
with
$\unicode[STIX]{x1D70E}_{1}$
with
![]() $\unicode[STIX]{x1D70F}_{1}$
. As
$\unicode[STIX]{x1D70F}_{1}$
. As
![]() $L_{\unicode[STIX]{x1D70E}_{1}}=(1-q)L_{\unicode[STIX]{x1D70F}_{1}}$
and mult
$L_{\unicode[STIX]{x1D70E}_{1}}=(1-q)L_{\unicode[STIX]{x1D70F}_{1}}$
and mult
![]() $(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{1}})=1$
, it follows that the contributions of
$(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{1}})=1$
, it follows that the contributions of
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{1}$
cancel each other out.
$\unicode[STIX]{x1D70E}_{1}$
cancel each other out.
5.2.2 On false poles contributed by
 $X_{2}$
-facets
$X_{2}$
-facets
Case 1. The candidate pole is contributed by an isolated
![]() $X_{2}$
-facet.
$X_{2}$
-facet.
Lemma 13. Let
![]() $\unicode[STIX]{x1D70F}$
be a facet with vertexes
$\unicode[STIX]{x1D70F}$
be a facet with vertexes
![]() $p=(N(\unicode[STIX]{x1D70F})/2,0,0),q=(x_{1},0,2)$
and
$p=(N(\unicode[STIX]{x1D70F})/2,0,0),q=(x_{1},0,2)$
and
![]() $r=(x_{2},2,0)$
, where
$r=(x_{2},2,0)$
, where
![]() $N(\unicode[STIX]{x1D70F})/2-x_{1}$
and
$N(\unicode[STIX]{x1D70F})/2-x_{1}$
and
![]() $N(\unicode[STIX]{x1D70F})/2-x_{2}$
are odd. If the order of
$N(\unicode[STIX]{x1D70F})/2-x_{2}$
are odd. If the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
does not divide
$\bar{\unicode[STIX]{x1D712}}$
does not divide
![]() $N(\unicode[STIX]{x1D70F})/2$
and is different from
$N(\unicode[STIX]{x1D70F})/2$
and is different from
![]() $2$
, then
$2$
, then
![]() $\unicode[STIX]{x1D70F}$
does not contribute an actual pole to
$\unicode[STIX]{x1D70F}$
does not contribute an actual pole to
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
.
$Z_{f}(\unicode[STIX]{x1D712},s)$
.
Proof. It follows immediately from Fact 2 that the vertexes
![]() $p$
,
$p$
,
![]() $q$
and
$q$
and
![]() $r$
do not contribute. Using Lemma 7, one also verifies that the edge
$r$
do not contribute. Using Lemma 7, one also verifies that the edge
![]() $qr$
does not contribute. We now show that the contributions of
$qr$
does not contribute. We now show that the contributions of
![]() $\unicode[STIX]{x1D70E}_{1}:=pq$
,
$\unicode[STIX]{x1D70E}_{1}:=pq$
,
![]() $\unicode[STIX]{x1D70E}_{2}:=pr$
and the facet
$\unicode[STIX]{x1D70E}_{2}:=pr$
and the facet
![]() $\unicode[STIX]{x1D70F}$
cancel each other. As
$\unicode[STIX]{x1D70F}$
cancel each other. As
![]() $N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70F})$
, we have that mult
$N(\unicode[STIX]{x1D70E}_{1})=N(\unicode[STIX]{x1D70E}_{2})=N(\unicode[STIX]{x1D70F})$
, we have that mult
![]() $(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{1}})=\text{mult}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{2}})=1$
, and thus
$(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{1}})=\text{mult}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{2}})=1$
, and thus
One gets
 $$\begin{eqnarray}\displaystyle & \displaystyle L_{\unicode[STIX]{x1D70E}_{1}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{1}})+L_{\unicode[STIX]{x1D70E}_{2}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{2}})+L_{\unicode[STIX]{x1D70F}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Updownarrow & \displaystyle \nonumber\\ \displaystyle & \displaystyle (q-1)L_{\unicode[STIX]{x1D70F}}=-L_{\unicode[STIX]{x1D70E}_{1}}-L_{\unicode[STIX]{x1D70E}_{2}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle L_{\unicode[STIX]{x1D70E}_{1}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{1}})+L_{\unicode[STIX]{x1D70E}_{2}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{2}})+L_{\unicode[STIX]{x1D70F}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70F}})=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Updownarrow & \displaystyle \nonumber\\ \displaystyle & \displaystyle (q-1)L_{\unicode[STIX]{x1D70F}}=-L_{\unicode[STIX]{x1D70E}_{1}}-L_{\unicode[STIX]{x1D70E}_{2}}. & \displaystyle \nonumber\end{eqnarray}$$
The equality between these character sums is proved in Proposition 10. There,
![]() $\unicode[STIX]{x1D6FE}=0$
if the point
$\unicode[STIX]{x1D6FE}=0$
if the point
![]() $((x_{1}+x_{2})/2,1,1)$
is not in the support of
$((x_{1}+x_{2})/2,1,1)$
is not in the support of
![]() $f$
. Note that the condition
$f$
. Note that the condition
![]() $\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\neq 0$
in the statement of Proposition 10 follows from the nondegeneracy of
$\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FF}\neq 0$
in the statement of Proposition 10 follows from the nondegeneracy of
![]() $\overline{f}$
with respect to the edge
$\overline{f}$
with respect to the edge
![]() $qr$
.◻
$qr$
.◻
If
![]() $x_{1}=x_{2}=0$
(in which case the
$x_{1}=x_{2}=0$
(in which case the
![]() $X_{2}$
-facet is the only compact facet of
$X_{2}$
-facet is the only compact facet of
![]() $\unicode[STIX]{x1D6E4}_{0}$
), then we can prove something slightly stronger.
$\unicode[STIX]{x1D6E4}_{0}$
), then we can prove something slightly stronger.
Lemma 14. Let
![]() $\unicode[STIX]{x1D70F}$
be a facet with vertexes
$\unicode[STIX]{x1D70F}$
be a facet with vertexes
![]() $p=(N(\unicode[STIX]{x1D70F})/2,0,0),q=(0,0,2)$
and
$p=(N(\unicode[STIX]{x1D70F})/2,0,0),q=(0,0,2)$
and
![]() $r=(0,2,0)$
, where
$r=(0,2,0)$
, where
![]() $N(\unicode[STIX]{x1D70F})/2$
is odd. If the order of
$N(\unicode[STIX]{x1D70F})/2$
is odd. If the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
does not divide
$\bar{\unicode[STIX]{x1D712}}$
does not divide
![]() $N(\unicode[STIX]{x1D70F})/2$
, then
$N(\unicode[STIX]{x1D70F})/2$
, then
![]() $\unicode[STIX]{x1D70F}$
does not contribute an actual pole to
$\unicode[STIX]{x1D70F}$
does not contribute an actual pole to
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
.
$Z_{f}(\unicode[STIX]{x1D712},s)$
.
Proof. The previous proof remains valid, except for the conclusions that
![]() $q$
,
$q$
,
![]() $r$
and
$r$
and
![]() $\unicode[STIX]{x1D70E}_{3}:=qr$
do not contribute, where we used that the order of
$\unicode[STIX]{x1D70E}_{3}:=qr$
do not contribute, where we used that the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
is not
$\bar{\unicode[STIX]{x1D712}}$
is not
![]() $2$
. We show that the contributions cancel. Indeed, since
$2$
. We show that the contributions cancel. Indeed, since
![]() $\text{mult}(\unicode[STIX]{x1D6E5}_{q})=\text{mult}(\unicode[STIX]{x1D6E5}_{r})=\text{mult}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{3}})=N(\unicode[STIX]{x1D70F})/2$
, we have
$\text{mult}(\unicode[STIX]{x1D6E5}_{q})=\text{mult}(\unicode[STIX]{x1D6E5}_{r})=\text{mult}(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{3}})=N(\unicode[STIX]{x1D70F})/2$
, we have
 $$\begin{eqnarray}\displaystyle & \displaystyle S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{3}})=\frac{N}{(q-1)(q^{N(\unicode[STIX]{x1D70F})s+\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})}-1)}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle S(\unicode[STIX]{x1D6E5}_{q})=S(\unicode[STIX]{x1D6E5}_{r})=\frac{N}{(q-1)^{2}(q^{N(\unicode[STIX]{x1D70F})s+\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})}-1)}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{3}})=\frac{N}{(q-1)(q^{N(\unicode[STIX]{x1D70F})s+\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})}-1)}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle S(\unicode[STIX]{x1D6E5}_{q})=S(\unicode[STIX]{x1D6E5}_{r})=\frac{N}{(q-1)^{2}(q^{N(\unicode[STIX]{x1D70F})s+\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})}-1)}, & \displaystyle \nonumber\end{eqnarray}$$
for some common numerator
![]() $N$
. One gets
$N$
. One gets
 $$\begin{eqnarray}\displaystyle & \displaystyle L_{q}S(\unicode[STIX]{x1D6E5}_{q})+L_{r}S(\unicode[STIX]{x1D6E5}_{r})+L_{\unicode[STIX]{x1D70E}_{3}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{3}})=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Updownarrow & \displaystyle \nonumber\\ \displaystyle & \displaystyle (q-1)L_{\unicode[STIX]{x1D70E}_{3}}=-L_{q}-L_{r}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle L_{q}S(\unicode[STIX]{x1D6E5}_{q})+L_{r}S(\unicode[STIX]{x1D6E5}_{r})+L_{\unicode[STIX]{x1D70E}_{3}}S(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70E}_{3}})=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Updownarrow & \displaystyle \nonumber\\ \displaystyle & \displaystyle (q-1)L_{\unicode[STIX]{x1D70E}_{3}}=-L_{q}-L_{r}. & \displaystyle \nonumber\end{eqnarray}$$
This again follows from Proposition 10 (with
![]() $\unicode[STIX]{x1D6FC}=0$
).◻
$\unicode[STIX]{x1D6FC}=0$
).◻
Case 2. The candidate pole is contributed by two
![]() $X_{2}$
-facets sharing a
$X_{2}$
-facets sharing a
![]() $1$
-dimensional face.
$1$
-dimensional face.
Two different
![]() $X_{2}$
-facets
$X_{2}$
-facets
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D70F}^{\prime }$
can appear in a cluster in one way only, and this determines the entire Newton polyhedron, as shown in Figure 1. As in the proof of Lemma 13, we see that
$\unicode[STIX]{x1D70F}^{\prime }$
can appear in a cluster in one way only, and this determines the entire Newton polyhedron, as shown in Figure 1. As in the proof of Lemma 13, we see that
![]() $q$
,
$q$
,
![]() $r$
,
$r$
,
![]() $qr$
do not contribute. Therefore, the lemma also applies to this joint configuration.
$qr$
do not contribute. Therefore, the lemma also applies to this joint configuration.

Figure 1. Two
![]() $X_{2}$
-facets with 1-dimensional common face.
$X_{2}$
-facets with 1-dimensional common face.
5.2.3 On false poles contributed by
 $B_{1}$
-facets
$B_{1}$
-facets
In [Reference Bories and VeysBV, Proposition 9.6], it is shown that if a candidate pole contributed only by
![]() $B_{1}$
-facets is an actual pole of
$B_{1}$
-facets is an actual pole of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
, then it is contributed by two
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
, then it is contributed by two
![]() $B_{1}$
-facets with respect to different variables having a
$B_{1}$
-facets with respect to different variables having a
![]() $1$
-dimensional intersection. We revisit and extend this analysis, and show that even in that situation the candidate pole is almost always a false pole of
$1$
-dimensional intersection. We revisit and extend this analysis, and show that even in that situation the candidate pole is almost always a false pole of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
. We need this strengthening here, because for the holomorphy conjecture we want to verify whether or not
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
. We need this strengthening here, because for the holomorphy conjecture we want to verify whether or not
![]() $1/N_{j}$
gives rise to an eigenvalue of monodromy, rather than the quotient
$1/N_{j}$
gives rise to an eigenvalue of monodromy, rather than the quotient
![]() $\unicode[STIX]{x1D708}_{j}/N_{j}$
(which is potentially simplifiable). We also study when candidate poles of the global Igusa zeta function
$\unicode[STIX]{x1D708}_{j}/N_{j}$
(which is potentially simplifiable). We also study when candidate poles of the global Igusa zeta function
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
corresponding to
$Z_{f}(\unicode[STIX]{x1D712},s)$
corresponding to
![]() $B_{1}$
-facets are false poles.
$B_{1}$
-facets are false poles.
From the preliminary work in Section 5.2.1, one can derive the contributions of all possible clusters of
![]() $B_{1}$
-facets. We begin with the configuration studied (in the local case over
$B_{1}$
-facets. We begin with the configuration studied (in the local case over
![]() $\mathbb{Q}_{p}$
) in [Reference Bories and VeysBV, Proposition 9.6], which we mentioned at the beginning of this section.
$\mathbb{Q}_{p}$
) in [Reference Bories and VeysBV, Proposition 9.6], which we mentioned at the beginning of this section.
Case 1. The candidate pole is contributed by a configuration of
![]() $B_{1}$
-facets in which no two facets that share a
$B_{1}$
-facets in which no two facets that share a
![]() $1$
-dimensional face are
$1$
-dimensional face are
![]() $B_{1}$
only for different variables.
$B_{1}$
only for different variables.
For the contributions to the local Igusa zeta function, one can derive from Facts 1, 4 and 5 that the candidate pole is a false pole. For the global Igusa zeta function, one in addition uses Facts 6 and 7.

Figure 2. Two compact
![]() $B_{1}$
-facets with respect to different variables, sharing a line segment.
$B_{1}$
-facets with respect to different variables, sharing a line segment.
Case 2. The candidate pole is contributed by exactly two compact
![]() $B_{1}$
-facets with respect to different variables, having a line segment in common.
$B_{1}$
-facets with respect to different variables, having a line segment in common.
If the common line segment is compact, then the configuration is as in Figure 2, with
![]() $A=(.\,,0,.),B=(1,1,b),C=(0,.\,,.)$
and
$A=(.\,,0,.),B=(1,1,b),C=(0,.\,,.)$
and
![]() $D=(0,0,a)$
. If the order of
$D=(0,0,a)$
. If the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
$\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
![]() $a$
, then it follows from Facts 1–5 that the candidate pole is a false pole of
$a$
, then it follows from Facts 1–5 that the candidate pole is a false pole of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
.
$Z_{f}(\unicode[STIX]{x1D712},s)$
.

Figure 3. Two noncompact
![]() $B_{1}$
-facets with respect to different variables, sharing a noncompact line segment.
$B_{1}$
-facets with respect to different variables, sharing a noncompact line segment.
Case 3. The candidate pole is contributed by two noncompact
![]() $B_{1}$
-facets with respect to different variables, having a line segment in common.
$B_{1}$
-facets with respect to different variables, having a line segment in common.
If the common line segment is noncompact, then the configuration is as in Figure 3, with
![]() $A=(.\,,0,.),B=(0,.\,,.)$
and
$A=(.\,,0,.),B=(0,.\,,.)$
and
![]() $C=(1,1,.)$
. For the contributions to the local Igusa zeta function, one deduces from Facts 1, 4 and 5 that the candidate pole is a false pole. For the global Igusa zeta function, one also has to use Facts 6 and 7.
$C=(1,1,.)$
. For the contributions to the local Igusa zeta function, one deduces from Facts 1, 4 and 5 that the candidate pole is a false pole. For the global Igusa zeta function, one also has to use Facts 6 and 7.
If the common line segment is compact, then its vertexes are given by
![]() $A=(0,0,a)$
and
$A=(0,0,a)$
and
![]() $B=(1,1,b)$
. If the order of
$B=(1,1,b)$
. If the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
$\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
![]() $a$
, then by Facts 1–7, it follows again that the candidate pole is not an actual pole of
$a$
, then by Facts 1–7, it follows again that the candidate pole is not an actual pole of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
.
$Z_{f}(\unicode[STIX]{x1D712},s)$
.
Case 4. The candidate pole is contributed by one compact
![]() $B_{1}$
-facet and one noncompact
$B_{1}$
-facet and one noncompact
![]() $B_{1}$
-facet with respect to different variables, having a line segment in common.
$B_{1}$
-facet with respect to different variables, having a line segment in common.
Again, using Facts 1–7, one finds that the candidate pole is a false pole of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
and
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
when the order of
$Z_{f}(\unicode[STIX]{x1D712},s)$
when the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
$\bar{\unicode[STIX]{x1D712}}$
is not a divisor of
![]() $a$
.
$a$
.
Case 5. The candidate pole is contributed by at least two
![]() $B_{1}$
-facets with respect to different variables, having a line segment in common.
$B_{1}$
-facets with respect to different variables, having a line segment in common.
As in Case 2 the contributions of
![]() $\unicode[STIX]{x1D70F}_{1}:=ABD$
,
$\unicode[STIX]{x1D70F}_{1}:=ABD$
,
![]() $\unicode[STIX]{x1D70F}_{2}:=BCD$
and
$\unicode[STIX]{x1D70F}_{2}:=BCD$
and
![]() $\unicode[STIX]{x1D70F}_{1}\cap \unicode[STIX]{x1D70F}_{2}:=BD$
are all equal to
$\unicode[STIX]{x1D70F}_{1}\cap \unicode[STIX]{x1D70F}_{2}:=BD$
are all equal to
![]() $0$
, one can deduce the fakeness of the candidate pole also when there are other
$0$
, one can deduce the fakeness of the candidate pole also when there are other
![]() $B_{1}$
-facets having a
$B_{1}$
-facets having a
![]() $1$
-dimensional intersection with
$1$
-dimensional intersection with
![]() $\unicode[STIX]{x1D70F}_{1}$
or
$\unicode[STIX]{x1D70F}_{1}$
or
![]() $\unicode[STIX]{x1D70F}_{2}$
.◻
$\unicode[STIX]{x1D70F}_{2}$
.◻
5.3 Holomorphy conjecture for nondegenerate surface singularities
We are now ready to prove the main result of this article.
Theorem 15. Let
![]() $F$
be a number field, and let
$F$
be a number field, and let
![]() $f(x,y,z)\in {\mathcal{O}}_{F}[x,y,z]$
be a polynomial that is nondegenerate over
$f(x,y,z)\in {\mathcal{O}}_{F}[x,y,z]$
be a polynomial that is nondegenerate over
![]() $\mathbb{C}$
with respect to the compact faces (resp. the faces) of its Newton polyhedron at the origin
$\mathbb{C}$
with respect to the compact faces (resp. the faces) of its Newton polyhedron at the origin
![]() $\unicode[STIX]{x1D6E4}_{0}$
. Let
$\unicode[STIX]{x1D6E4}_{0}$
. Let
![]() $K$
be a nonarchimedean completion of
$K$
be a nonarchimedean completion of
![]() $F$
with valuation ring
$F$
with valuation ring
![]() $R$
(with maximal ideal
$R$
(with maximal ideal
![]() $P$
) and residue field
$P$
) and residue field
![]() $\mathbb{F}_{q}$
, and suppose that
$\mathbb{F}_{q}$
, and suppose that
![]() $\bar{f}:=f\text{ mod }P$
is nondegenerate over
$\bar{f}:=f\text{ mod }P$
is nondegenerate over
![]() $\mathbb{F}_{q}$
with respect to the compact faces (resp. the faces) of
$\mathbb{F}_{q}$
with respect to the compact faces (resp. the faces) of
![]() $\unicode[STIX]{x1D6E4}_{0}$
. Let
$\unicode[STIX]{x1D6E4}_{0}$
. Let
![]() $\unicode[STIX]{x1D712}$
be a nontrivial character of
$\unicode[STIX]{x1D712}$
be a nontrivial character of
![]() $R^{\times }$
which is trivial on
$R^{\times }$
which is trivial on
![]() $1+P$
. Let
$1+P$
. Let
![]() $\unicode[STIX]{x1D70F}$
be a facet of
$\unicode[STIX]{x1D70F}$
be a facet of
![]() $\unicode[STIX]{x1D6E4}_{0}$
. If
$\unicode[STIX]{x1D6E4}_{0}$
. If
![]() $-\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})$
is the real part of a pole of
$-\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})/N(\unicode[STIX]{x1D70F})$
is the real part of a pole of
![]() $Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
$Z_{f,0}(\unicode[STIX]{x1D712},s)$
(resp.
![]() $Z_{f}(\unicode[STIX]{x1D712},s)$
), then the order of
$Z_{f}(\unicode[STIX]{x1D712},s)$
), then the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of an eigenvalue of monodromy at some point of
$\unicode[STIX]{x1D712}$
divides the order of an eigenvalue of monodromy at some point of
![]() $f^{-1}\{0\}$
.
$f^{-1}\{0\}$
.
Proof. We first suppose that
![]() $\unicode[STIX]{x1D70F}$
is a compact facet. If every
$\unicode[STIX]{x1D70F}$
is a compact facet. If every
![]() $1$
-dimensional V-face of
$1$
-dimensional V-face of
![]() $\unicode[STIX]{x1D6E4}_{0}$
is contained in a compact facet, then we know from Formula (3) that the zeta function of monodromy at the origin is a product of polynomials. If
$\unicode[STIX]{x1D6E4}_{0}$
is contained in a compact facet, then we know from Formula (3) that the zeta function of monodromy at the origin is a product of polynomials. If
![]() $\unicode[STIX]{x1D70F}$
is not a union of simplices of type
$\unicode[STIX]{x1D70F}$
is not a union of simplices of type
![]() $B_{1}$
or
$B_{1}$
or
![]() $X_{2}$
, then Proposition 12 implies that the order of
$X_{2}$
, then Proposition 12 implies that the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of an eigenvalue of monodromy of
$\unicode[STIX]{x1D712}$
divides the order of an eigenvalue of monodromy of
![]() $f^{-1}\{0\}$
at the origin.
$f^{-1}\{0\}$
at the origin.
If
![]() $\unicode[STIX]{x1D70F}$
is of type
$\unicode[STIX]{x1D70F}$
is of type
![]() $B_{1}$
, then we found in Section 5.2.3 that there is a point
$B_{1}$
, then we found in Section 5.2.3 that there is a point
![]() $p=(0,0,a)$
in the configuration that is not the intersection of two
$p=(0,0,a)$
in the configuration that is not the intersection of two
![]() $1$
-dimensional V-faces in the same compact facet, and second that the order of
$1$
-dimensional V-faces in the same compact facet, and second that the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
divides this
$\bar{\unicode[STIX]{x1D712}}$
divides this
![]() $a$
. This means that the factor
$a$
. This means that the factor
![]() $1-t^{a}$
appears in
$1-t^{a}$
appears in
![]() $\unicode[STIX]{x1D701}_{f,0}(t)$
, and so one finds that the order of
$\unicode[STIX]{x1D701}_{f,0}(t)$
, and so one finds that the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
$\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
![]() $f^{-1}\{0\}$
at the origin.
$f^{-1}\{0\}$
at the origin.
If
![]() $\unicode[STIX]{x1D70F}$
is not a simplicial facet but a union of simplices of type
$\unicode[STIX]{x1D70F}$
is not a simplicial facet but a union of simplices of type
![]() $B_{1}$
, then, up to permutation of the coordinates, the facet
$B_{1}$
, then, up to permutation of the coordinates, the facet
![]() $\unicode[STIX]{x1D70F}$
should have as vertexes
$\unicode[STIX]{x1D70F}$
should have as vertexes
![]() $A=(a,0,0),B=(c,d,0),C=(b,1,1)$
and
$A=(a,0,0),B=(c,d,0),C=(b,1,1)$
and
![]() $D=(e,0,f)$
for
$D=(e,0,f)$
for
![]() $a,\ldots ,f\in \mathbb{Z}_{{\geqslant}0}$
, and so one has
$a,\ldots ,f\in \mathbb{Z}_{{\geqslant}0}$
, and so one has
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{1}\cup \unicode[STIX]{x1D70F}_{2}$
, with
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{1}\cup \unicode[STIX]{x1D70F}_{2}$
, with
![]() $\unicode[STIX]{x1D70F}_{1}:=ABD$
and
$\unicode[STIX]{x1D70F}_{1}:=ABD$
and
![]() $\unicode[STIX]{x1D70F}_{2}:=ACD$
two
$\unicode[STIX]{x1D70F}_{2}:=ACD$
two
![]() $B_{1}$
-simplices. Notice that the factor
$B_{1}$
-simplices. Notice that the factor
![]() $1-t^{a}$
appears in
$1-t^{a}$
appears in
![]() $\unicode[STIX]{x1D701}_{f,0}(t)$
. If the order of
$\unicode[STIX]{x1D701}_{f,0}(t)$
. If the order of
![]() $\unicode[STIX]{x1D712}$
divides
$\unicode[STIX]{x1D712}$
divides
![]() $a$
, then one finds indeed that the order of
$a$
, then one finds indeed that the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
$\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
![]() $f^{-1}\{0\}$
at the origin.
$f^{-1}\{0\}$
at the origin.
Therefore, suppose now that the order of
![]() $\unicode[STIX]{x1D712}$
does not divide
$\unicode[STIX]{x1D712}$
does not divide
![]() $a$
. The facet
$a$
. The facet
![]() $\unicode[STIX]{x1D70F}$
is also the union of the simplices
$\unicode[STIX]{x1D70F}$
is also the union of the simplices
![]() $ABC$
and
$ABC$
and
![]() $BCD$
. The simplex
$BCD$
. The simplex
![]() $BCD$
is never of type
$BCD$
is never of type
![]() $X_{2}$
. If one of these simplices is not of type
$X_{2}$
. If one of these simplices is not of type
![]() $B_{1}$
, then it follows by Proposition 12 that the order of
$B_{1}$
, then it follows by Proposition 12 that the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
$\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
![]() $f^{-1}\{0\}$
at the origin. If
$f^{-1}\{0\}$
at the origin. If
![]() $ABC$
and
$ABC$
and
![]() $BCD$
are both of type
$BCD$
are both of type
![]() $B_{1}$
, then one then easily checks that
$B_{1}$
, then one then easily checks that
![]() $d$
or
$d$
or
![]() $f$
should be equal to
$f$
should be equal to
![]() $1$
; hence,
$1$
; hence,
![]() $\text{gcd}(d,f)=1$
. We have
$\text{gcd}(d,f)=1$
. We have
As
![]() $\text{Aff}(\unicode[STIX]{x1D70F}_{1})=\text{Aff}(\unicode[STIX]{x1D70F}_{2})$
, we have that
$\text{Aff}(\unicode[STIX]{x1D70F}_{1})=\text{Aff}(\unicode[STIX]{x1D70F}_{2})$
, we have that
![]() $N(\unicode[STIX]{x1D70F})$
divides
$N(\unicode[STIX]{x1D70F})$
divides
![]() $a\cdot \text{gcd}(d,f)=a$
. As we suppose that
$a\cdot \text{gcd}(d,f)=a$
. As we suppose that
![]() $\unicode[STIX]{x1D70F}$
contributes a pole, it follows that the order of
$\unicode[STIX]{x1D70F}$
contributes a pole, it follows that the order of
![]() $\unicode[STIX]{x1D712}$
divides
$\unicode[STIX]{x1D712}$
divides
![]() $N(\unicode[STIX]{x1D70F})$
, and so again the order of
$N(\unicode[STIX]{x1D70F})$
, and so again the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
$\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
![]() $f^{-1}\{0\}$
at the origin.
$f^{-1}\{0\}$
at the origin.
If
![]() $\unicode[STIX]{x1D70F}$
is of type
$\unicode[STIX]{x1D70F}$
is of type
![]() $X_{2}$
, say with vertexes
$X_{2}$
, say with vertexes
![]() $p=(N(\unicode[STIX]{x1D70F})/2,0,0),q=(x_{1},0,2)$
and
$p=(N(\unicode[STIX]{x1D70F})/2,0,0),q=(x_{1},0,2)$
and
![]() $r=(x_{2},2,0)$
, then
$r=(x_{2},2,0)$
, then
![]() $F_{\unicode[STIX]{x1D70F}}=1-t^{N(\unicode[STIX]{x1D70F})/2}$
, and hence
$F_{\unicode[STIX]{x1D70F}}=1-t^{N(\unicode[STIX]{x1D70F})/2}$
, and hence
![]() $e^{-2\unicode[STIX]{x1D70B}i/(N(\unicode[STIX]{x1D70F})/2)}$
is an eigenvalue of monodromy of
$e^{-2\unicode[STIX]{x1D70B}i/(N(\unicode[STIX]{x1D70F})/2)}$
is an eigenvalue of monodromy of
![]() $f^{-1}\{0\}$
at the origin. Thus, if the order of
$f^{-1}\{0\}$
at the origin. Thus, if the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
divides
$\bar{\unicode[STIX]{x1D712}}$
divides
![]() $N(\unicode[STIX]{x1D70F})/2$
, then we are done. If the order of
$N(\unicode[STIX]{x1D70F})/2$
, then we are done. If the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
does not divide
$\bar{\unicode[STIX]{x1D712}}$
does not divide
![]() $N(\unicode[STIX]{x1D70F})/2$
, then by Lemma 13, the order of
$N(\unicode[STIX]{x1D70F})/2$
, then by Lemma 13, the order of
![]() $\bar{\unicode[STIX]{x1D712}}$
should be equal to
$\bar{\unicode[STIX]{x1D712}}$
should be equal to
![]() $2$
. In this situation,
$2$
. In this situation,
![]() $N(\unicode[STIX]{x1D70F})/2$
is odd and
$N(\unicode[STIX]{x1D70F})/2$
is odd and
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
are even, while by Lemma 14, we can assume that
$x_{2}$
are even, while by Lemma 14, we can assume that
![]() $0\neq x_{1}\geqslant x_{2}$
. Let
$0\neq x_{1}\geqslant x_{2}$
. Let
![]() $\unicode[STIX]{x1D70F}^{\prime }$
be the other facet that contains the segment
$\unicode[STIX]{x1D70F}^{\prime }$
be the other facet that contains the segment
![]() $qr$
. Notice that
$qr$
. Notice that
![]() $\unicode[STIX]{x1D70F}^{\prime }$
is not of type
$\unicode[STIX]{x1D70F}^{\prime }$
is not of type
![]() $B_{1}$
and that
$B_{1}$
and that
![]() $N(\unicode[STIX]{x1D70F}^{\prime })$
is even.
$N(\unicode[STIX]{x1D70F}^{\prime })$
is even.
We first suppose that
![]() $\unicode[STIX]{x1D70F}^{\prime }$
is compact. If
$\unicode[STIX]{x1D70F}^{\prime }$
is compact. If
![]() $\unicode[STIX]{x1D70F}^{\prime }$
is not of type
$\unicode[STIX]{x1D70F}^{\prime }$
is not of type
![]() $X_{2}$
, then it follows from Proposition 12 that
$X_{2}$
, then it follows from Proposition 12 that
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F}^{\prime })}$
is a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F}^{\prime })}$
is a zero of
![]() $F_{\unicode[STIX]{x1D70F}^{\prime }}$
, and so the order of
$F_{\unicode[STIX]{x1D70F}^{\prime }}$
, and so the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
$\unicode[STIX]{x1D712}$
divides the order of some eigenvalue of monodromy of
![]() $f^{-1}\{0\}$
at the origin. If
$f^{-1}\{0\}$
at the origin. If
![]() $\unicode[STIX]{x1D70F}^{\prime }$
is of type
$\unicode[STIX]{x1D70F}^{\prime }$
is of type
![]() $X_{2}$
, then the configuration is as in Figure 1. In this situation, we get
$X_{2}$
, then the configuration is as in Figure 1. In this situation, we get
and so again the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of an eigenvalue of monodromy of
$\unicode[STIX]{x1D712}$
divides the order of an eigenvalue of monodromy of
![]() $f^{-1}\{0\}$
at the origin.
$f^{-1}\{0\}$
at the origin.
Suppose now that
![]() $\unicode[STIX]{x1D70F}^{\prime }$
is not compact. Then, necessarily,
$\unicode[STIX]{x1D70F}^{\prime }$
is not compact. Then, necessarily,
![]() $x_{1}>x_{2}$
, and
$x_{1}>x_{2}$
, and
At a generic point
![]() $(0,0,c)$
of the hypersurface, the polynomial
$(0,0,c)$
of the hypersurface, the polynomial
![]() $g(x,y,z):=f(x,y,z-c)$
is still nondegenerate with respect to the compact faces of its Newton polyhedron at the origin (see Lemma 2), and its Newton polyhedron is the projection onto
$g(x,y,z):=f(x,y,z-c)$
is still nondegenerate with respect to the compact faces of its Newton polyhedron at the origin (see Lemma 2), and its Newton polyhedron is the projection onto
![]() $\{z=0\}$
of the Newton polyhedron of
$\{z=0\}$
of the Newton polyhedron of
![]() $f$
times
$f$
times
![]() $\mathbb{R}_{+}$
. From Varchenko’s formula, one sees that this projected polyhedron fully determines
$\mathbb{R}_{+}$
. From Varchenko’s formula, one sees that this projected polyhedron fully determines
![]() $\unicode[STIX]{x1D701}_{g,0}(t)$
. Using [Reference Lemahieu and Van ProeyenLVP2, Proposition 5], it follows that
$\unicode[STIX]{x1D701}_{g,0}(t)$
. Using [Reference Lemahieu and Van ProeyenLVP2, Proposition 5], it follows that
![]() $\unicode[STIX]{x1D701}_{g,0}(t)$
contains the factor
$\unicode[STIX]{x1D701}_{g,0}(t)$
contains the factor
![]() $1/(1-t^{x_{1}})$
. We thus have that the order of
$1/(1-t^{x_{1}})$
. We thus have that the order of
![]() $\unicode[STIX]{x1D712}$
divides the order of an eigenvalue of monodromy at a point of the hypersurface in the neighborhood of the origin.
$\unicode[STIX]{x1D712}$
divides the order of an eigenvalue of monodromy at a point of the hypersurface in the neighborhood of the origin.
It is easy to check that a nonsimplicial facet cannot decompose into a union of
![]() $X_{2}$
-facets.
$X_{2}$
-facets.
Suppose now that there is a
![]() $1$
-dimensional V-face
$1$
-dimensional V-face
![]() $\unicode[STIX]{x1D70E}$
, say in the coordinate plane
$\unicode[STIX]{x1D70E}$
, say in the coordinate plane
![]() $z=0$
, which is not contained in a compact facet. If
$z=0$
, which is not contained in a compact facet. If
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is a zero of
![]() $F_{\unicode[STIX]{x1D70E}}$
(we use the notation
$F_{\unicode[STIX]{x1D70E}}$
(we use the notation
![]() $F_{\unicode[STIX]{x1D70E}}$
as if
$F_{\unicode[STIX]{x1D70E}}$
as if
![]() $\unicode[STIX]{x1D70E}$
was a facet of a two-dimensional Newton polyhedron in the plane
$\unicode[STIX]{x1D70E}$
was a facet of a two-dimensional Newton polyhedron in the plane
![]() $z=0$
), then we choose
$z=0$
), then we choose
![]() $c\in \mathbb{C}$
close to zero such that
$c\in \mathbb{C}$
close to zero such that
![]() $g(x,y,z):=f(x,y,z-c)$
is still nondegenerate with respect to its Newton polyhedron at the origin (see Lemma 2). Then, we have
$g(x,y,z):=f(x,y,z-c)$
is still nondegenerate with respect to its Newton polyhedron at the origin (see Lemma 2). Then, we have
with
![]() $F_{\unicode[STIX]{x1D70E}}=1/\text{polynomial}$
(except in the case where
$F_{\unicode[STIX]{x1D70E}}=1/\text{polynomial}$
(except in the case where
![]() $\unicode[STIX]{x1D70E}$
contains two vertexes on coordinate axes, but in this case the same conclusion holds), and so we find that
$\unicode[STIX]{x1D70E}$
contains two vertexes on coordinate axes, but in this case the same conclusion holds), and so we find that
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is an eigenvalue of monodromy of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is an eigenvalue of monodromy of
![]() $f$
at
$f$
at
![]() $(0,0,c)$
.
$(0,0,c)$
.
Finally, let
![]() $\unicode[STIX]{x1D70F}$
be noncompact. Again, by the nondegeneracy argument (Lemma 2), we can reduce the dimension and conclude that
$\unicode[STIX]{x1D70F}$
be noncompact. Again, by the nondegeneracy argument (Lemma 2), we can reduce the dimension and conclude that
![]() $e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is an eigenvalue of monodromy of
$e^{-2\unicode[STIX]{x1D70B}i/N(\unicode[STIX]{x1D70F})}$
is an eigenvalue of monodromy of
![]() $f$
at a point in the neighborhood of the origin.◻
$f$
at a point in the neighborhood of the origin.◻