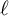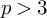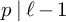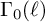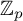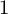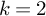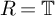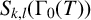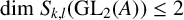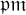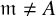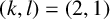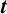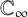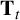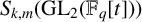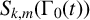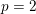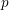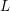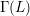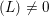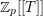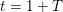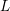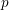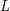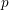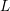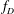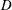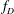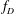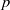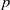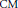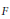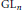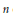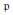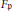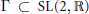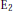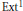Refine search
Actions for selected content:
14 results
Asymptotics and sign patterns of Hecke polynomial coefficients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 914-926
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE EISENSTEIN IDEAL OF WEIGHT k AND RANKS OF HECKE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 31 March 2023, pp. 983-1017
- Print publication:
- March 2024
-
- Article
- Export citation
NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 50-68
- Print publication:
- August 2023
-
- Article
- Export citation
HECKE OPERATORS AND DRINFELD CUSP FORMS OF LEVEL
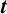 $\boldsymbol {t}$
$\boldsymbol {t}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 June 2022, pp. 184-195
- Print publication:
- April 2023
-
- Article
- Export citation
A TRACE FORMULA FOR HECKE OPERATORS ON VECTOR-VALUED MODULAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 143-165
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
Level 1 Hecke algebras of modular forms modulo
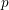 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 397-415
- Print publication:
- March 2015
-
- Article
- Export citation
Big Galois representations and
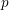 $p$-adic
$p$-adic 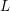 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 13 November 2014, pp. 603-664
- Print publication:
- April 2015
-
- Article
- Export citation
On a completed generating function of locally harmonic Maass forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 749-762
- Print publication:
- May 2014
-
- Article
- Export citation
Computing level one Hecke eigensystems (mod
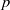 $p$ )
$p$ )
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 246-270
-
- Article
-
- You have access
- Export citation
QUASIMODULAR FORMS AND COHOMOLOGY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 15 December 2011, pp. 150-163
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
A Remark on a Modular Analogue of the Sato–Tate Conjecture
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 2 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 234-242
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation
A Hypergraph with Commuting Partial Laplacians
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 4 / 01 December 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-397
- Print publication:
- 01 December 2001
-
- Article
-
- You have access
- Export citation
Hecke Operators on Jacobi-like Forms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 3 / 01 September 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 282-291
- Print publication:
- 01 September 2001
-
- Article
-
- You have access
- Export citation
Hecke Operations and the Adams E2 -Term Based on Elliptic Cohomology
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 2 / 01 June 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-138
- Print publication:
- 01 June 1999
-
- Article
-
- You have access
- Export citation