Refine search
Actions for selected content:
7 results
Ramanujan-type series for
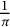 $\frac {1}{\pi }$, revisited
$\frac {1}{\pi }$, revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 350-368
- Print publication:
- June 2024
-
- Article
- Export citation
Exact formulae and Turán inequalities for Vafa–Witten invariants of
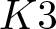 $K3$ surfaces
$K3$ surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. 845-861
-
- Article
- Export citation
THE SHIMURA CURVE OF DISCRIMINANT 15 AND TOPOLOGICAL AUTOMORPHIC FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 05 February 2015, e3
-
- Article
-
- You have access
- Open access
- Export citation
A twisted topological trace formula for Hecke operators and liftings from symplectic to general linear groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 65-120
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
A Modular Quintic Calabi–Yau Threefold of Level 55
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 3 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 616-633
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation
On the Modularity of Three Calabi–Yau Threefolds With Bad Reduction at 11
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 2 / 01 June 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 296-312
- Print publication:
- 01 June 2006
-
- Article
-
- You have access
- Export citation
On modularity of rigid and nonrigid Calabi-Yau varieties associated to the Root Lattice A 4
-
- Journal:
- Nagoya Mathematical Journal / Volume 179 / 2005
- Published online by Cambridge University Press:
- 11 January 2016, pp. 103-146
- Print publication:
- 2005
-
- Article
-
- You have access
- Export citation
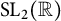
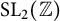
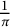
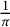
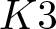
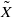 by gluing together 2
by gluing together 2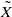 and get formulas for the traces of Hecke operators ℋ acting on the cohomology of
and get formulas for the traces of Hecke operators ℋ acting on the cohomology of 

