Refine search
Actions for selected content:
21 results
VORONOI COMPLEXES IN HIGHER DIMENSIONS, COHOMOLOGY OF
 $GL_N(\mathbb{Z} )$ FOR
$GL_N(\mathbb{Z} )$ FOR  $N\geqslant 8$ AND THE TRIVIALITY OF
$N\geqslant 8$ AND THE TRIVIALITY OF  $K_8(\mathbb{Z} )$
$K_8(\mathbb{Z} )$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-26
-
- Article
- Export citation
Explicit spectral gap for Hecke congruence covers of arithmetic Schottky surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 September 2025, pp. 1-41
-
- Article
- Export citation
Packable hyperbolic surfaces with symmetries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 103-113
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
Directions in orbits of geometrically finite hyperbolic subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 23 November 2020, pp. 277-316
- Print publication:
- September 2021
-
- Article
- Export citation
Arithmeticity of discrete subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2561-2590
- Print publication:
- September 2021
-
- Article
- Export citation
Ideal Uniform Polyhedra in
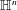 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 465-492
- Print publication:
- April 2021
-
- Article
- Export citation
Arithmeticity of the monodromy of some Kodaira fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 114-157
- Print publication:
- January 2020
-
- Article
- Export citation
Computing fundamental domains for the Bruhat–Tits tree for
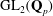 ${\rm GL}_2(\mathbf{Q}_p)$ ,
${\rm GL}_2(\mathbf{Q}_p)$ , 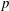 $p$ -adic automorphic forms, and the canonical embedding of Shimura curves
$p$ -adic automorphic forms, and the canonical embedding of Shimura curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 1-23
-
- Article
-
- You have access
- Export citation
Conjugacy Classes and Binary Quadratic Forms for the Hecke Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 570-583
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
Modular subgroups, dessins d’enfants and elliptic K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 271-318
-
- Article
-
- You have access
- Export citation
Products of pairs of Dehn twists and maximal real Lefschetz fibrations
-
- Journal:
- Nagoya Mathematical Journal / Volume 210 / June 2013
- Published online by Cambridge University Press:
- 11 January 2016, pp. 83-132
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Quantifying residual finiteness of arithmetic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 907-920
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
TORSION IN ARITHMETIC FUCHSIAN GROUPS
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 22 February 2006, pp. 14-30
- Print publication:
- February 2006
-
- Article
- Export citation
THE MINIMUM INDEX OF A NON-CONGRUENCE SUBGROUP OF SL2 OVER AN ARITHMETIC DOMAIN. II: THE RANK ZERO CASES
-
- Journal:
- Journal of the London Mathematical Society / Volume 71 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 04 February 2005, pp. 53-68
- Print publication:
- February 2005
-
- Article
- Export citation
HOLOMORPHIC ALMOST MODULAR FORMS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 5 / September 2004
- Published online by Cambridge University Press:
- 24 August 2004, pp. 647-655
- Print publication:
- September 2004
-
- Article
- Export citation
Perfect Non-Extremal Riemann Surfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 1 / 01 March 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-125
- Print publication:
- 01 March 2000
-
- Article
-
- You have access
- Export citation
Quadratic Integers and Coxeter Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 6 / 01 December 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1307-1336
- Print publication:
- 01 December 1999
-
- Article
-
- You have access
- Export citation
Trace Classes and Quadratic Forms in the Modular Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 2 / 01 June 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 202-212
- Print publication:
- 01 June 1994
-
- Article
-
- You have access
- Export citation
Classification of Maximal Fuchsian Subsgroups of Some Bianchi Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 3 / 01 September 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-422
- Print publication:
- 01 September 1991
-
- Article
-
- You have access
- Export citation
















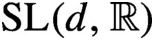
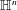
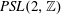
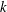
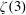
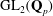
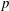
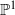
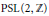
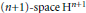
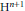
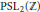
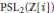
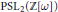
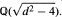 The algorithm mentioned above then provides a new straightforward computational procedure for determining
The algorithm mentioned above then provides a new straightforward computational procedure for determining 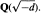 A complete classification of conjugacy classes of maximal non-elementary Fuchsian subgroups of PSL(2,
A complete classification of conjugacy classes of maximal non-elementary Fuchsian subgroups of PSL(2, 