Hostname: page-component-cb9f654ff-plnhv Total loading time: 0.001 Render date: 2025-08-28T22:49:49.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugacy Classes and Binary Quadratic Forms for the Hecke Groups

Published online by Cambridge University Press:  20 November 2018

Giabao Hoang  and
Wendell Ressler
Giabao Hoang
Affiliation:
Department of Mathematics, Franklin & Marshall College, Lancaster, PA 17604 e-mail: giabao.hoang@fandm.edu wendell.ressler@fandm.edu
Wendell Ressler
Affiliation:
Department of Mathematics, Franklin & Marshall College, Lancaster, PA 17604 e-mail: giabao.hoang@fandm.edu wendell.ressler@fandm.edu
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give a lower bound with respect to block length for the trace of non-elliptic conjugacy classes of the Hecke groups. One consequence of our bound is that there are finitely many conjugacy classes of a given trace in anyHecke group. We show that another consequence of our bound is that class numbers are finite for related hyperbolic 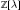$\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$ -binary quadratic forms. We give canonical class representatives and calculate class numbers for some classes of hyperbolic 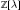$\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$ -binary quadratic forms.

Keywords

11F0611E1611A55Hecke groupsconjugacy classquadratic forms

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 570 - 583
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Choie, Yj. and Zagier, D., Rational period functions for PSL(2; Z). Contemp. Math. 143, Amer. Math. Soc., Providence, RI, 1993, 89–108.Google Scholar
[2] Culp-Ressler, Wendell, Rational period functions on the Hecke groups. Ramanujan J. 5 (2001, 281–294. http://dx.doi.org/10.1023/A:1012926712079 Google Scholar
[3] Fine, Benjamin, Trace classes and quadratic forms in the modular group. Canad. Math. Bull. 37 (1994, 202–212. http://dx.doi.org/10.4153/CMB-1994-030-1 Google Scholar
[4] Hecke, E., U¨ber die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung. Math. Ann. 112 (1936, 664–699. http://dx.doi.org/10.1007/BF01565437 Google Scholar
[5] Lehner, Joseph, A short course in automorphic functions. Holt, Rinehart andWinston, New York, 1966.Google Scholar
[6] Magnus, Wilhelm, Karrass, Abraham, and Solitar, Donald, Combinatorial group theory: Presentations of groups in terms of generators and relations. Interscience Publishers [JohnWiley & Sons, Inc.], New York–London–Sydney, 1966.Google Scholar
[7] Meier, Holger and Rosenberger, Gerhard, Hecke-Integrale mit rationalen periodischen Funktionen und Dirichlet–Reihen mit Funktionalgleichung. Results Math. 7 (1984, 209–233.Google Scholar
[8] Parson, L. Alayne, Rational period functions and indefinite binary quadratic forms. III. Contemp. Math. 143, Amer. Math. Soc., Providence, RI, 1993, 109–116.Google Scholar
[9] Ressler, Wendell, On binary quadratic forms and the Hecke groups. Int. J. Number Theory 5 (2009, 1401–1418. http://dx.doi.org/10.1142/S1793042109002730 Google Scholar
[10] Ressler, Wendell, A Hecke correspondence theorem for automorphic integrals with symmetric rational period functions on the Hecke groups. J. Number Theory 130 (2010, 2732–2744. http://dx.doi.org/10.1016/j.jnt.2010.06.009 Google Scholar
[11] Rosen, David, A class of continued fractions associated with certain properly discontinuous groups. Duke Math. J. 21 (1954, 549–563. http://dx.doi.org/10.1215/S0012-7094-54-02154-7 Google Scholar
[12] Schmidt, Thomas A., Remarks on the Rosen _-continued fractions. In: Number theory with an emphasis on the Markoff spectrum (Provo, UT, 1991), Lecture Notes Pure Appl. Math. 147, Dekker, New York, 1993, 227–238.Google Scholar
[13] Schmidt, Thomas A. and Sheingorn, Mark, Length spectra of the Hecke triangle groups. Math. Z. 220 (1995, 369–397. http://dx.doi.org/10.1007/BF02572621 Google Scholar
[14] Zagier, D. B., Zetafunktionen und quadratische Körper. Springer-Verlag, Berlin, 1981.Google Scholar