Refine search
Actions for selected content:
3 results
The Values of Modular Functions and Modular Forms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 4 / 01 December 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 526-535
- Print publication:
- 01 December 2006
-
- Article
-
- You have access
- Export citation
Modular Parametrizations of Elliptic Curves
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 3 / 01 September 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 372-384
- Print publication:
- 01 September 1985
-
- Article
-
- You have access
- Export citation
The Construction of Automorphic Forms From the Derivatives of a Given Form II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 3 / 01 September 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 306-316
- Print publication:
- 01 September 1985
-
- Article
-
- You have access
- Export citation
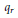
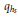
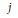
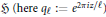
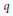
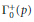
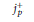
 have a "modular parametrization," i.e. for some
have a "modular parametrization," i.e. for some 