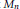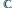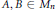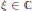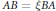Refine search
Actions for selected content:
4 results
ON MAXIMAL SUBGROUPS OF IDEMPOTENT-GENERATED SEMIGROUPS ASSOCIATED WITH BIORDERED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 January 2022, pp. 341-343
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
SHEAF RECURSION AND A SEPARATION THEOREM
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 18 August 2014, pp. 882-907
- Print publication:
- September 2014
-
- Article
- Export citation
General Preservers of Quasi-Commutativity
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 4 / 01 August 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 758-786
- Print publication:
- 01 August 2010
-
- Article
-
- You have access
- Export citation
Strongly Projective Graphs
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 4 / 01 August 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 757-768
- Print publication:
- 01 August 2002
-
- Article
-
- You have access
- Export citation