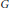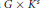Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Okrasa, Karolina
and
Rzaͅżewski, Paweł
2021.
Fine-Grained Complexity of the Graph Homomorphism Problem for Bounded-Treewidth Graphs.
SIAM Journal on Computing,
Vol. 50,
Issue. 2,
p.
487.