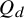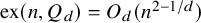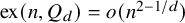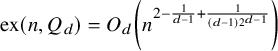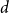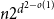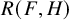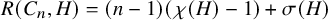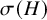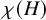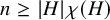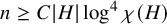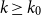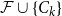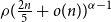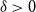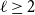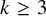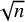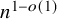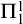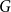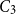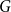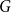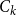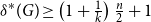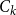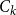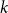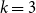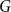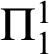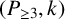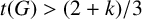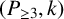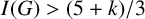Refine search
Actions for selected content:
48 results
Chi-Boundedness of graphs containing no cycles with k chords
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 November 2025, e189
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graph operations and a unified method for Turán-type problems on paths, cycles, and matchings
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-27
-
- Article
- Export citation
LONGEST CYCLES AND LONGEST CHORDLESS CYCLES IN
 $2$-CONNECTED GRAPHS
$2$-CONNECTED GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 27 February 2025, pp. 401-409
- Print publication:
- December 2025
-
- Article
- Export citation
A SUFFICIENT CONDITION FOR PANCYCLIC GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 220-226
- Print publication:
- October 2025
-
- Article
- Export citation
Long induced paths in expanders
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 276-282
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTREMAL GRAPHS FOR DEGREE SUMS AND DOMINATING CYCLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 205-211
- Print publication:
- April 2025
-
- Article
- Export citation
Strong digraph groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 991-1000
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalization of Bondy’s pancyclicity theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 554-563
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Turán number of the hypercube
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Many Hamiltonian subsets in large graphs with given density
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 110-120
-
- Article
- Export citation
Disparity-persistence and the multistep friendship paradox
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 290-298
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramsey numbers of cycles versus general graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 February 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bipartite-ness under smooth conditions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 546-558
-
- Article
- Export citation
Cycles of many lengths in Hamiltonian graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 31 August 2022, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALMOST THEOREMS OF HYPERARITHMETIC ANALYSIS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 664-696
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transversal Ck-factors in subgraphs of the balanced blow-up of Ck
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1031-1047
-
- Article
- Export citation
THEOREMS OF HYPERARITHMETIC ANALYSIS AND ALMOST THEOREMS OF HYPERARITHMETIC ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 31 March 2022, pp. 133-149
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Short proofs for long induced paths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 870-878
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper Lie automorphisms of incidence algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 07 February 2022, pp. 702-715
- Print publication:
- September 2022
-
- Article
- Export citation
TOUGHNESS, ISOLATED TOUGHNESS AND PATH FACTORS IN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 03 December 2021, pp. 195-202
- Print publication:
- October 2022
-
- Article
- Export citation