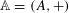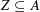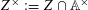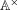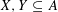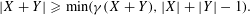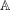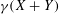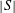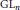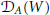Refine search
Actions for selected content:
25 results
A note on weight systems which are quantum states
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 1109-1121
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariants for metabelian groups of prime power exponent, colorings, and stairs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 December 2021, pp. 267-297
- Print publication:
- February 2023
-
- Article
- Export citation
A proof of the linear Arithmetic Fundamental Lemma for
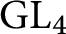 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 381-427
- Print publication:
- April 2022
-
- Article
- Export citation
A METRIC VERSION OF SCHLICHTING’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1607-1613
- Print publication:
- December 2020
-
- Article
- Export citation
FRIEZE PATTERNS WITH COEFFICIENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 March 2020, e17
-
- Article
-
- You have access
- Open access
- Export citation
Tropical friezes and the index in higher homological algebra
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 23-49
- Print publication:
- July 2021
-
- Article
- Export citation
DEGREE OF THE
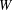 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 186-200
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Boardman–Vogt tensor products of absolutely free operads
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 367-385
- Print publication:
- February 2020
-
- Article
- Export citation
Twisted Brauer monoids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 731-750
- Print publication:
- August 2018
-
- Article
- Export citation
Co-maximal Graphs of Subgroups of Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 12-25
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
THE IDEMPOTENT-GENERATED SUBSEMIGROUP OF THE KAUFFMAN MONOID
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 673-683
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Irreducible decomposition of binomial ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1319-1332
- Print publication:
- June 2016
-
- Article
- Export citation
CAUCHY–DAVENPORT TYPE THEOREMS FOR SEMIGROUPS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 May 2015, pp. 1-12
- Print publication:
- 2016
-
- Article
- Export citation
ESTIMATION AND COMPUTATION WITH MATRICES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 175-176
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Eigenvalues of Hermitian matrices and equivariant cohomology of Grassmannians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 1569-1582
- Print publication:
- September 2013
-
- Article
- Export citation
DESCRIPTION OF SIMPLE MODULES FOR SCHUR SUPERALGEBRA S(2|2)
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 695-719
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
A GRAPHICAL DESCRIPTION OF (Dn,An−1) KAZHDAN–LUSZTIG POLYNOMIALS
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 313-340
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation
Groups acting simply transitively on vertex sets of hyperbolic triangular buildings
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 101-112
-
- Article
-
- You have access
- Export citation
Interval Pattern Avoidance for Arbitrary Root Systems
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 4 / 01 December 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 757-762
- Print publication:
- 01 December 2010
-
- Article
-
- You have access
- Export citation
Generalized Descent Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 4 / 01 December 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 535-546
- Print publication:
- 01 December 2007
-
- Article
-
- You have access
- Export citation
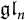
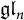
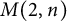
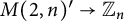
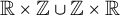
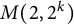
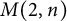
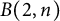
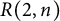
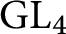
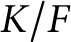
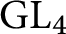
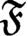
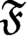
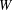
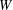
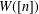
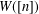
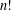
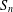
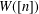
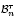 , comparing and contrasting it with the structure of the (untwisted) Brauer monoid
, comparing and contrasting it with the structure of the (untwisted) Brauer monoid 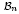 . We characterize Green's relations and pre-orders on
. We characterize Green's relations and pre-orders on