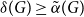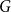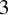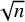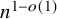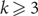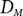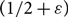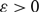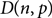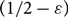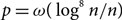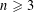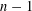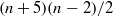Refine search
Actions for selected content:
22 results
Tight Hamilton cycles with high discrepancy
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 30 May 2025, pp. 565-584
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cycle Partitions in Dense Regular Digraphs and Oriented Graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hamiltonicity of sparse pseudorandom graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 25 March 2025, pp. 596-620
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SUFFICIENT CONDITION FOR PANCYCLIC GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 220-226
- Print publication:
- October 2025
-
- Article
- Export citation
Rainbow Hamiltonicity in uniformly coloured perturbed digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 624-642
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalization of Bondy’s pancyclicity theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 554-563
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On oriented cycles in randomly perturbed digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 157-178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cycles of many lengths in Hamiltonian graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 31 August 2022, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A proof of a conjecture of Gyárfás, Lehel, Sárközy and Schelp on Berge-cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 654-669
-
- Article
- Export citation
Counting Hamilton cycles in Dirac hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 17 December 2020, pp. 631-653
-
- Article
- Export citation
Hamiltonian Berge cycles in random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 08 September 2020, pp. 228-238
-
- Article
- Export citation
Dirac’s theorem for random regular graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 17-36
-
- Article
- Export citation
Hamiltonicity in random directed graphs is born resilient
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 24 June 2020, pp. 900-942
-
- Article
- Export citation
CHARACTER GRAPHS WITH NONBIPARTITE HAMILTONIAN COMPLEMENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 25 November 2019, pp. 91-95
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
ALTERNATING AND SYMMETRIC GROUPS WITH EULERIAN GENERATING GRAPH
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 10 November 2017, e24
-
- Article
-
- You have access
- Open access
- Export citation
On the Maximum Number of Spanning Copies of an Orientation in a Tournament
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 06 June 2017, pp. 775-796
-
- Article
- Export citation
On the Swap-Distances of Different Realizations of a Graphical Degree Sequence
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 3 / May 2013
- Published online by Cambridge University Press:
- 05 April 2013, pp. 366-383
-
- Article
- Export citation
WIENER INDEX AND TRACEABLE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 December 2012, pp. 380-383
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Getting a Directed Hamilton Cycle Two Times Faster
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 04 May 2012, pp. 773-801
-
- Article
- Export citation
Proof of the Hamiltonicity-Trace Conjecture for Singularly Perturbed Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 901-910
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation