Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-26T04:00:19.453Z Has data issue: false hasContentIssue false
  • English
  • Français

ALTERNATING AND SYMMETRIC GROUPS WITH EULERIAN GENERATING GRAPH

Part of: Permutation groups Graph theory

Published online by Cambridge University Press:  10 November 2017

ANDREA LUCCHINI  and
CLAUDE MARION
ANDREA LUCCHINI
Affiliation:
Dipartimento di Matematica Tullio Levi-Civita, Università degli Studi di Padova, 35121-I Padova, Italy; lucchini@math.unipd.it
CLAUDE MARION
Affiliation:
Dipartimento di Matematica Tullio Levi-Civita, Università degli Studi di Padova, 35121-I Padova, Italy; marion@math.unipd.it

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a finite group 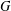$G$, the generating graph 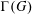$\unicode[STIX]{x1D6E4}(G)$ of 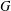$G$ has as vertices the (nontrivial) elements of 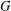$G$ and two vertices are adjacent if and only if they are distinct and generate 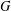$G$ as group elements. In this paper we investigate properties about the degrees of the vertices of 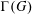$\unicode[STIX]{x1D6E4}(G)$ when 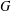$G$ is an alternating group or a symmetric group of degree $n$. In particular, we determine the vertices of 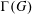$\unicode[STIX]{x1D6E4}(G)$ having even degree and show that 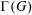$\unicode[STIX]{x1D6E4}(G)$ is Eulerian if and only if 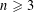$n\geqslant 3$ and $n$ and 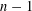$n-1$ are not equal to a prime number congruent to 3 modulo 4.

MSC classification

Primary: 20B35: Subgroups of symmetric groups
Secondary: 05C45: Eulerian and Hamiltonian graphs 20B10: Characterization theorems 05C07: Vertex degrees
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e24
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Aschbacher, M. and Guralnick, R., ‘Some applications of the first cohomology group’, J. Algebra 90 (1984), 446–460.CrossRefGoogle Scholar
Basile, A., ‘Second maximal subgroups of the finite alternating and symmetric groups’, PhD Thesis, The Australian National University, 2001.Google Scholar
Binder, G., ‘The bases of the symmetric group’, Izv. Vyssh. Uchebn. Zaved. Mat. 78 (1968), 19–25.Google Scholar
Breuer, T., Guralnick, R. and Kantor, W., ‘Probabilistic generation of finite simple groups II’, J. Algebra 320 (2008), 443–494.Google Scholar
Breuer, T., Guralnick, R., Lucchini, A., Maróti, A. and Nagy, G., ‘Hamiltonian cycles in the generating graphs of finite groups’, Bull. Lond. Math. Soc. 42 (2010), 621–633.CrossRefGoogle Scholar
Conway, J., Curtis, R., Norton, S., Parker, R. and Wilson, R., Atlas of Finite Groups (Oxford University Press, Eynsham, 1985).Google Scholar
Detomi, E. and Lucchini, A., ‘Profinite groups with multiplicative probabilistic zeta function’, J. Lond. Math. Soc. 70 (2004), 165–181.CrossRefGoogle Scholar
Dixon, J. and Mortimer, B., Permutation Groups, Graduate Texts in Mathematics, 163 (Springer, New York, 1996).Google Scholar
Guest, S., Morris, J., Praeger, C. and Spiga, P., ‘Affine transformations of finite vector spaces with large orders or few cycles’, J. Pure Appl. Algebra 219 (2015), 308–330.CrossRefGoogle Scholar
Guest, S., Morris, J., Praeger, C. and Spiga, P., ‘On the maximum orders of elements of finite almost simple groups and primitive permutation groups’, Trans. Amer. Math. Soc. 367 (2015), 7665–7694.Google Scholar
Guralnick, R. and Kantor, W., ‘Probabilistic generation of finite simple groups’, J. Algebra 234 (2000), 743–792.CrossRefGoogle Scholar
Hall, P., ‘The Eulerian functions of a group’, J. Math. Oxford Ser. 7 (1936), 134–151.Google Scholar
Hawkes, T., Isaacs, I. and Özaydin, M., ‘On the Möbius function of a finite group’, Rocky Mountain J. Math. 19 (1989), 1003–1034.CrossRefGoogle Scholar
Kantor, W., ‘Linear groups containing a Singer cycle’, J. Algebra 62 (1980), 232–234.Google Scholar
Liebeck, M., Praeger, C. and Saxl, J., ‘A classification of the maximal subgroups of the finite alternating and symmetric groups’, J. Algebra 111 (1987), 365–383.CrossRefGoogle Scholar
Liebeck, M., Praeger, C. and Saxl, J., ‘On the O’Nan–Scott theorem for finite primitive permutation groups’, J. Aust. Math. Soc. 44 (1988), 389–396.Google Scholar
Lucchini, A., ‘The X-Dirichlet polynomial of a finite group’, J. Group Theory 8 (2005), 171–188.CrossRefGoogle Scholar
Miller, G., ‘On the groups generated by two operators’, Bull. Amer. Math. Soc. 7 (1901), 424–426.CrossRefGoogle Scholar
Praeger, C., ‘An O’Nan–Scott theorem for finite quasiprimitive permutation groups and an application to 2-arc transitive graphs’, J. Lond. Math. Soc. 47 (1993), 227–239.CrossRefGoogle Scholar
Praeger, C., ‘Finite quasiprimitive graphs’, inSurvey in Combinatorics, 1997 (London), London Mathematical Society Lecture Note Series, 241 (Cambridge University Press, Cambridge, 1997), 65–85.Google Scholar
Steinberg, R., ‘Generators for simple groups’, Canad. J. Math. 14 (1962), 277–283.Google Scholar