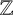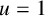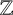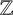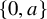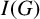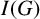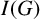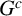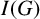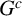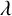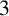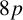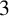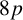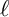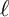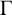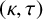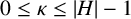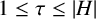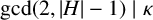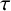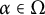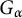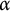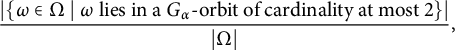Refine search
Actions for selected content:
77 results
On the gcd-graphs over polynomial rings
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-28
-
- Article
- Export citation
The Ceresa period from tropical homology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Splines on Cayley graphs of the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 June 2025, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AUTOMORPHISM GROUPS OF BICOSET DIGRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 30-46
- Print publication:
- August 2025
-
- Article
- Export citation
ELEMENTARY PROOFS OF THE DIAMETER BOUNDS FOR POWER GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 505-508
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Restricted sumsets in multiplicative subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON NEIGHBOURHOODS IN THE ENHANCED POWER GRAPH ASSOCIATED WITH A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 149-154
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cubical setting for discrete homotopy theory, revisited
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 21 March 2025, pp. 2856-2903
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPANNING TREES IN
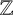 $\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
$\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 108-144
- Print publication:
- February 2025
-
- Article
- Export citation
Strong digraph groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 991-1000
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Undecidability of polynomial inequalities in weighted graph homomorphism densities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOMOLOGICAL LINEAR QUOTIENTS AND EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 291-302
- Print publication:
- October 2024
-
- Article
- Export citation
NOWHERE-ZERO
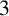 $3$-FLOWS IN CAYLEY GRAPHS OF ORDER
$3$-FLOWS IN CAYLEY GRAPHS OF ORDER 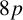 $8p$
$8p$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1-11
- Print publication:
- August 2024
-
- Article
- Export citation
CORRECTION TO ‘ON THE COMPLEMENT OF THE ZERO-DIVISOR GRAPH OF A PARTIALLY ORDERED SET’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 170-173
- Print publication:
- February 2024
-
- Article
- Export citation
CAYLEY GRAPHS AND GRAPHICAL REGULAR REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 161-162
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON THE DISTRIBUTION OF IWASAWA INVARIANTS ASSOCIATED TO MULTIGRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 48-90
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantum symmetries of Cayley graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. 655-686
- Print publication:
- September 2023
-
- Article
- Export citation
Erdős–Ko–Rado theorem in Peisert-type graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 176-187
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON REGULAR SETS IN CAYLEY GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 1-5
- Print publication:
- February 2024
-
- Article
- Export citation
Finite transitive groups having many suborbits of cardinality at most 2 and an application to the enumeration of Cayley graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 30 January 2023, pp. 345-366
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation