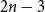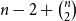1. Introduction
Consider a group of agents that initially each know a unique secret. The agents then make one-to-one telephone calls during which they always share all the secrets they know. So-called gossip protocols in this simple model provide an efficient way to spread information using peer-to-peer communication (Hedetniemi et al. Reference Hedetniemi, Hedetniemi and Liestman1988).
Even when the gossiping agents only exchange secrets and no knowledge about secrets, they can obtain higher-order knowledge: they can get to know what other agents know, or even what other agents know about yet other agents (van Ditmarsch et al. Reference van Ditmarsch, Gattinger and Ramezanian2023). It is known that without synchronization via a global clock one cannot obtain common knowledge by peer-to-peer communication (Halpern and Moses Reference Halpern and Moses1990). Therefore, we also cannot obtain common knowledge in gossiping. It is folklore that in gossiping only first-order shared knowledge can be achieved when only exchanging secrets. In this article, we make this result precise using epistemic logic. Footnote 1
We start with some examples that illustrate how agents can obtain higher-order knowledge.
Example 1. Suppose we have a set of four agents
![]() $\{a,b,c,d\}$
. Consider the sequence of calls
$\{a,b,c,d\}$
. Consider the sequence of calls
![]() $ab.cd.ac.bd.ad.bc.ab.cd$
and the results shown in Table 1. After the fourth call bd everyone is an expert, that is, they know all secrets. In both of the last two calls ab and cd, the two agents involved become so-called super experts, that is, they know that everyone knows all secrets. In this example, two agents become super experts in the same call. This is not always the case.
$ab.cd.ac.bd.ad.bc.ab.cd$
and the results shown in Table 1. After the fourth call bd everyone is an expert, that is, they know all secrets. In both of the last two calls ab and cd, the two agents involved become so-called super experts, that is, they know that everyone knows all secrets. In this example, two agents become super experts in the same call. This is not always the case.
Table 1. Results of
![]() $ab.cd.ac.bd.ad.bc.ab.cd$
. A lower case y in column x means x knows the secret of y; an upper case Y means x knows that y is an expert. Therefore, “abcd” denotes an expert and “ABCD” denotes a super expert
$ab.cd.ac.bd.ad.bc.ab.cd$
. A lower case y in column x means x knows the secret of y; an upper case Y means x knows that y is an expert. Therefore, “abcd” denotes an expert and “ABCD” denotes a super expert
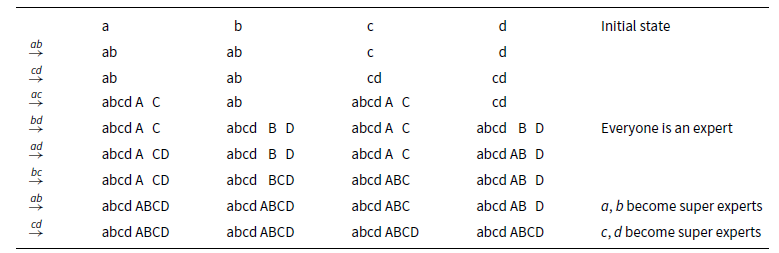
More interestingly, an agent may learn that another agent is an expert without calling that agent, both in a call wherein she becomes an expert but also when she already is an expert. We will call this a lucky call, and this notion plays a key role in our contribution.
Example 2. Again suppose we have a set of four agents
![]() $\{a,b,c,d\}$
and consider the call sequence
$\{a,b,c,d\}$
and consider the call sequence
![]() $ac.ad.ac.bc.ac$
, with results shown in Table 2. Here, agent a learns in the final call ac that a, b, and c are experts. Because b is not involved in this call we say that this is a lucky call and say that a is lucky about b. We will show that this sequence is typical for a non-expert to be lucky. We will show that multiple non-expert agents can be lucky in a call sequence, but each of them can be lucky at most once.
$ac.ad.ac.bc.ac$
, with results shown in Table 2. Here, agent a learns in the final call ac that a, b, and c are experts. Because b is not involved in this call we say that this is a lucky call and say that a is lucky about b. We will show that this sequence is typical for a non-expert to be lucky. We will show that multiple non-expert agents can be lucky in a call sequence, but each of them can be lucky at most once.
Table 2. Results of
![]() $ac.ad.ac.bc.ac$
including a lucky call
$ac.ad.ac.bc.ac$
including a lucky call

Example 3. Once more consider four agents
![]() $\{a,b,c,d\}$
and now call sequence
$\{a,b,c,d\}$
and now call sequence
![]() $ab.cd.bd.ad.ac$
, of which the results are shown in Table 3. Agent d becomes an expert in the call bd. Agent a becomes an expert in the call ad after that. In that call, she learns that d already was an expert so that there must be yet another agent who is an expert. But she is uncertain whether this is agent b or agent c. In final call ac, expert agent a calls the non-expert c, so she also learns in that call that from b and c, agent b must have been the one who made d an expert. Therefore, agent a is lucky about b in that call. Agent a also becomes a super expert in her lucky call. We will see that this rules out that any other agent is subsequently lucky.
$ab.cd.bd.ad.ac$
, of which the results are shown in Table 3. Agent d becomes an expert in the call bd. Agent a becomes an expert in the call ad after that. In that call, she learns that d already was an expert so that there must be yet another agent who is an expert. But she is uncertain whether this is agent b or agent c. In final call ac, expert agent a calls the non-expert c, so she also learns in that call that from b and c, agent b must have been the one who made d an expert. Therefore, agent a is lucky about b in that call. Agent a also becomes a super expert in her lucky call. We will see that this rules out that any other agent is subsequently lucky.
Table 3. Results of
![]() $ab.cd.bd.ad.ac$
$ab.cd.bd.ad.ac$

In a synchronous setting where agents are aware when calls happen that do not involve them, lucky calls are not a surprising phenomenon. A typical example is found in van Ditmarsch et al. (Reference van Ditmarsch, Gattinger and Ramezanian2023, Example 12): given call sequence
![]() $ab.ac.cd.ab.bc.ab$
, in the fourth call, ab agent a learns that agent b was not involved in the third call that also did not involve her. Therefore, a learns that the third call must have been cd, after which c and d became experts. Agent a is lucky twice in a single call!
$ab.ac.cd.ab.bc.ab$
, in the fourth call, ab agent a learns that agent b was not involved in the third call that also did not involve her. Therefore, a learns that the third call must have been cd, after which c and d became experts. Agent a is lucky twice in a single call!
In the asynchronous setting, we consider here, where agents only observe their own calls, we find the existence of lucky calls more surprising.
The existence of lucky calls makes it harder to get results for reaching higher-order epistemic goals and to get results for optimality. If an agent is lucky in a call, she learns more than intuitively expected from that call. There is information leakage. But is it leaking enough to reach higher-order knowledge, if a sufficient number of agents are lucky often enough? Also, a lucky agent can be saved by the effort of an additional call to the agent she is lucky about in order to get to know that all agents are experts. Does this allow shorter call sequences for everybody to get to know that all agents are experts, if a sufficient number of agents are lucky often enough? In this contribution, we show that the answer to both questions is negative. Informally, we can say: being lucky does not help.
This article is structured as follows. We discuss related work in Section 2 and provide the syntax and semantics of our epistemic logic and other basic definitions, in Section 3. In Section 4, we introduce notions describing how the calls in a given call sequence are causally related. In Section 5, we then define and characterize lucky calls. This section is more structured than other sections as it is longer. In particular, a great deal of effort goes into characterizing when expert agents can be lucky. Using all these results, in Section 6, we show that “everyone knows that everyone knows that everyone knows all secrets” is unsatisfiable, and finally in Section 7 that
![]() $2n-3$
calls are optimal to reach the epistemic goal “someone knows that everyone knows all secrets” and that
$2n-3$
calls are optimal to reach the epistemic goal “someone knows that everyone knows all secrets” and that
![]() $n - 2 + \binom{n}{2}$
calls are optimal to reach the epistemic goal “everyone knows that everyone knows all secrets.”
$n - 2 + \binom{n}{2}$
calls are optimal to reach the epistemic goal “everyone knows that everyone knows all secrets.”
2. Related Work
The “gossip problem” as introduced above is also known as the “telephone problem” and goes back (at least) to the article (Tijdeman Reference Tijdeman1971) from 1971. The main classical result is that only a linear amount of calls, namely
![]() $2n-4$
if we have
$2n-4$
if we have
![]() $n \geq 4$
agents, is needed to ensure that everyone knows all secrets. We refer to Hedetniemi et al. (Reference Hedetniemi, Hedetniemi and Liestman1988) for a survey of variants of the gossip problem, for example, over different graphs or using broadcasting.
$n \geq 4$
agents, is needed to ensure that everyone knows all secrets. We refer to Hedetniemi et al. (Reference Hedetniemi, Hedetniemi and Liestman1988) for a survey of variants of the gossip problem, for example, over different graphs or using broadcasting.
Most of the classical results assume a central scheduler, that is, an authority that decides in which order calls should be made. More recently, decentralized gossip has been studied, where agents decide on their own whom they should call next. Moreover, multiple logics have been developed to analyze the gossip problem and protocols (Apt et al. Reference Apt, Grossi and van der Hoek2015; Apt and Wojtczak Reference Apt, Wojtczak and Lang2017, Reference Apt and Wojtczak2018; Attamah et al. Reference Attamah, van Ditmarsch, Grossi, van der Hoek, Moss and Ramanujam2017; van Ditmarsch et al. Reference van Ditmarsch, Gattinger, Kuijer and Pardo2019, Reference van Ditmarsch, van der Hoek and Kuijer2020). Some of these logics include not only statements to say that agents know a secret, but they also provide general “an agent knows that
![]() $\varphi$
” modalities common in epistemic logics and thereby allow us to discuss the higher-order knowledge effects of gossip.
$\varphi$
” modalities common in epistemic logics and thereby allow us to discuss the higher-order knowledge effects of gossip.
The logics available for the analysis of gossip differ in their semantics, and many of them come with parameters to obtain different variants. For example, we need to decide whether callers only know what set of secrets they hold after a call (merge-then-inspect) or whether they also know what the other caller contributed to that output (inspect-then-merge), which is more informative (Apt et al. Reference Apt, Grossi and van der Hoek2015, Reference Apt, Grossi, van der Hoek, Barthe, Sutcliffe and Veanes2018; Attamah et al. Reference Attamah, van Ditmarsch, Grossi and van der Hoek2014; van Ditmarsch et al. Reference van Ditmarsch, van Eijck, Pardo, Ramezanian and Schwarzentruber2017). Here, we always assume inspect-then-merge. Besides individual and shared knowledge, one can also consider common knowledge in gossip (Apt and Wojtczak Reference Apt, Wojtczak and Lang2017, Reference Apt, Wojtczak and Moss2019), which we will not use here. Another crucial parameter is the presence of a global clock: in synchronous gossip, agents know a lot more than in asynchronous, truly distributed systems (Apt et al. Reference Apt, Grossi and van der Hoek2015; Apt and Wojtczak Reference Apt and Wojtczak2018; van Ditmarsch et al. Reference van Ditmarsch, van Eijck, Pardo, Ramezanian and Schwarzentruber2017). Here, we only consider the asynchronous case. Compared to related work, our focus here is not the study of different protocols, but we still use epistemic logic to determine what agents know, by reasoning about indistinguishable call sequences.
The question which higher-order knowledge can be achieved by communication between agents goes back to the classic problem of the Byzantine Generals (Lamport et al. Reference Lamport, Shostak and Pease1982). In general, it is impossible to achieve common knowledge in an asynchronous distributed system, as shown in Halpern and Moses (Reference Halpern and Moses1990). However, shared knowledge can be achieved by messages of the form “I know that this other agent knows that ”. This has been studied in Herzig and Maffre (Reference Herzig and Maffre2017) and Cooper et al. (Reference Cooper, Herzig, Maffre, Maris and Régnier2019), wherein agents inform each other what secrets other agents know and who knows that, etc. Concretely, among n agents shared knowledge of level (depth) k can be achieved by
![]() $(k + 1)(n - 2)$
many calls. It should be mentioned here that “agent a knows the secret of agent b” is level 1 in their representation (as in some other works, such as Attamah et al. Reference Attamah, van Ditmarsch, Grossi, van der Hoek, Moss and Ramanujam2017), whereas in our setting “agent a knows the secret of agent b” is represented as atomic information of epistemic level/depth 0 (as in most other works on epistemic gossip, e.g., also in Apt et al. Reference Apt, Grossi, van der Hoek, Barthe, Sutcliffe and Veanes2018, Apt and Wojtczak Reference Apt, Wojtczak and Lang2017, and van Ditmarsch et al. Reference van Ditmarsch, van Eijck, Pardo, Ramezanian and Schwarzentruber2017).
$(k + 1)(n - 2)$
many calls. It should be mentioned here that “agent a knows the secret of agent b” is level 1 in their representation (as in some other works, such as Attamah et al. Reference Attamah, van Ditmarsch, Grossi, van der Hoek, Moss and Ramanujam2017), whereas in our setting “agent a knows the secret of agent b” is represented as atomic information of epistemic level/depth 0 (as in most other works on epistemic gossip, e.g., also in Apt et al. Reference Apt, Grossi, van der Hoek, Barthe, Sutcliffe and Veanes2018, Apt and Wojtczak Reference Apt, Wojtczak and Lang2017, and van Ditmarsch et al. Reference van Ditmarsch, van Eijck, Pardo, Ramezanian and Schwarzentruber2017).
In our contribution, we only allow agents to exchange secrets and do not allow them to exchange any other kind of information.
Our result is most related to Apt and Wojtczak (Reference Apt and Wojtczak2018) and van Ditmarsch et al. (Reference van Ditmarsch, van der Hoek and Kuijer2020) who both investigate when the truth of formulas stabilizes during gossip protocol execution, including the case of the most general gossip protocol where any call can be made at any time and where agents only observe their own calls (setting
![]() $\langle\bullet,\Diamond,\beta\rangle$
in van Ditmarsch et al. Reference van Ditmarsch, van der Hoek and Kuijer2020, also called asynchronous
$\langle\bullet,\Diamond,\beta\rangle$
in van Ditmarsch et al. Reference van Ditmarsch, van der Hoek and Kuijer2020, also called asynchronous
![]() $\mathsf{ANY}$
in van Ditmarsch et al. Reference van Ditmarsch, Gattinger and Ramezanian2023). That case is the same setting as ours.
$\mathsf{ANY}$
in van Ditmarsch et al. Reference van Ditmarsch, Gattinger and Ramezanian2023). That case is the same setting as ours.
By different methods, the authors of Apt and Wojtczak (Reference Apt and Wojtczak2018) and those of van Ditmarsch et al. (Reference van Ditmarsch, van der Hoek and Kuijer2020) demonstrate that making new calls no longer affects the truth of epistemic formulas at some stage. Although the objectives of these publications were different, namely decidability of logics for gossip or correctness of gossip protocols, there is some overlap in methods. They show that in any (fairly scheduled) call sequence, with the standard call semantics that only secrets are exchanged in a call, at some stage further calls have no informational effect – such calls are redundant. This was relevant to observe for gossip protocols where the goal was that all agents became experts, because it showed that, in principle, even if one were to consider epistemic goals such as knowing that others are experts, things would eventually come to a stop. But they did not consider any specific epistemic goals.
In Apt and Wojtczak (Reference Apt and Wojtczak2018), only epistemic formulas of depth 1 were considered (the crucial result is Apt and Wojtczak Reference Apt and Wojtczak2018, Lemma 21), but here we focus on depth 2 and higher which in Apt and Wojtczak (Reference Apt and Wojtczak2018) is mentioned as a generalization for future work.
The authors of vanDitmarsch et al. (2020) considered epistemic formulas of arbitrary epistemic depth. However, there the comparison to our result stops: van Ditmarsch et al. (Reference van Ditmarsch, van der Hoek and Kuijer2020) (Prop. 5.5, Cor. 5.6) shows that formulas of any epistemic depth remain true forever or false forever after call sequences of certain length (bounded by a polynomial in terms of the number of agents). Hence, in particular, the formula
![]() $E\!E\!\mathit{Exp}_A$
which says “everyone knows that everyone knows that everyone knows all secrets” must remain true forever or false forever after further extending call sequences. But the authors of Ditmarsch et al. (2020) did not investigate specific formulas. In particular, they did not focus on the formula
$E\!E\!\mathit{Exp}_A$
which says “everyone knows that everyone knows that everyone knows all secrets” must remain true forever or false forever after further extending call sequences. But the authors of Ditmarsch et al. (2020) did not investigate specific formulas. In particular, they did not focus on the formula
![]() $E\!E\!\mathit{Exp}_A$
. Here, we show that
$E\!E\!\mathit{Exp}_A$
. Here, we show that
![]() $E\!E\!\mathit{Exp}_A$
remains false forever.
$E\!E\!\mathit{Exp}_A$
remains false forever.
3. Syntax and Semantics
We assume a finite set of at least four agents
![]() $A = \{a,b,c,d,\dots\}$
throughout this article. This assumption is needed for our main results. Some lemmas may also hold for fewer than four agents. Arbitrary agents are also denoted a, b, etc. We write
$A = \{a,b,c,d,\dots\}$
throughout this article. This assumption is needed for our main results. Some lemmas may also hold for fewer than four agents. Arbitrary agents are also denoted a, b, etc. We write
![]() $A{-}a$
for
$A{-}a$
for
![]() $A{\setminus}\{a\}$
and
$A{\setminus}\{a\}$
and
![]() $A{-}ab$
for
$A{-}ab$
for
![]() $A{\setminus}\{a,b\}$
. We also write
$A{\setminus}\{a,b\}$
. We also write
![]() $A{+}a$
for
$A{+}a$
for
![]() $A \cup\{a\}$
and
$A \cup\{a\}$
and
![]() $A{+}ab$
for
$A{+}ab$
for
![]() $A \cup\{a,b\}$
, and so on.
$A \cup\{a,b\}$
, and so on.
Each agent holds a single secret. The agents communicate with each other through telephone calls. During a call between two agents x and y, they exchange all the secrets that they knew before the call.
A call is a pair of agents
![]() $(a,b) \in A \times A$
, where
$(a,b) \in A \times A$
, where
![]() $a \neq b$
, for which we write ab. Agent a is the caller and agent b is the callee. Given call ab, call ba is the dual call. An agent a is involved in a call bc iff
$a \neq b$
, for which we write ab. Agent a is the caller and agent b is the callee. Given call ab, call ba is the dual call. An agent a is involved in a call bc iff
![]() $a=b$
or
$a=b$
or
![]() $a=c$
. In this contribution, the direction of the call does not matter, so it only matters if an agent is involved in a call. We will therefore arbitrarily write ab or ba for the call between a and b, where we often prefer the lexicographic order of agents. A call sequence is defined by induction: the empty sequence
$a=c$
. In this contribution, the direction of the call does not matter, so it only matters if an agent is involved in a call. We will therefore arbitrarily write ab or ba for the call between a and b, where we often prefer the lexicographic order of agents. A call sequence is defined by induction: the empty sequence
![]() $\epsilon$
is a call sequence. If
$\epsilon$
is a call sequence. If
![]() $\sigma$
is a call sequence and ab is a call, then
$\sigma$
is a call sequence and ab is a call, then
![]() $\sigma\kern-0.8pt{.}ab$
is a call sequence. We write
$\sigma\kern-0.8pt{.}ab$
is a call sequence. We write
![]() $|\sigma|$
to denote the length of a call sequence.
$|\sigma|$
to denote the length of a call sequence.
If
![]() $\sigma = \rho.\tau$
, then
$\sigma = \rho.\tau$
, then
![]() $\rho$
is a prefix of
$\rho$
is a prefix of
![]() $\sigma$
, denoted as
$\sigma$
, denoted as
![]() $\rho\sqsubseteq\sigma$
, and
$\rho\sqsubseteq\sigma$
, and
![]() $\tau$
is the complement of
$\tau$
is the complement of
![]() $\rho$
in
$\rho$
in
![]() $\sigma$
, where
$\sigma$
, where
![]() $\tau$
is also denoted
$\tau$
is also denoted
![]() $\sigma{\setminus}\rho$
.
$\sigma{\setminus}\rho$
.
Given call sequences
![]() $\tau$
and
$\tau$
and
![]() $\sigma$
, by induction on the length of
$\sigma$
, by induction on the length of
![]() $\sigma$
, we further define that
$\sigma$
, we further define that
![]() $\tau$
is a subsequence of
$\tau$
is a subsequence of
![]() $\sigma$
. This is the inductive definition:
$\sigma$
. This is the inductive definition:
![]() $\epsilon \subseteq \epsilon$
, and if
$\epsilon \subseteq \epsilon$
, and if
![]() $\tau \subseteq \sigma$
then
$\tau \subseteq \sigma$
then
![]() $\tau,\tau.ab \subseteq \sigma\kern-0.8pt{.}ab$
and
$\tau,\tau.ab \subseteq \sigma\kern-0.8pt{.}ab$
and
![]() $\tau,ab.\tau \subseteq ab.\sigma$
.
$\tau,ab.\tau \subseteq ab.\sigma$
.
Let
![]() $\sigma,\tau \subseteq \rho$
. Then,
$\sigma,\tau \subseteq \rho$
. Then,
![]() $\sigma \cup_\rho \tau \subseteq \rho$
, the union of
$\sigma \cup_\rho \tau \subseteq \rho$
, the union of
![]() $\sigma$
and
$\sigma$
and
![]() $\tau$
with respect to
$\tau$
with respect to
![]() $\rho$
, is the subsequence of
$\rho$
, is the subsequence of
![]() $\rho$
consisting of the calls occurring in
$\rho$
consisting of the calls occurring in
![]() $\sigma$
or in
$\sigma$
or in
![]() $\tau$
; and
$\tau$
; and
![]() $\sigma \setminus_\rho \tau$
, the difference of
$\sigma \setminus_\rho \tau$
, the difference of
![]() $\sigma$
and
$\sigma$
and
![]() $\tau$
with respect to
$\tau$
with respect to
![]() $\rho$
, is the subsequence of
$\rho$
, is the subsequence of
![]() $\rho$
consisting of the calls occurring in
$\rho$
consisting of the calls occurring in
![]() $\sigma$
and not occurring in
$\sigma$
and not occurring in
![]() $\tau$
. We similarly define
$\tau$
. We similarly define
![]() $\sigma_1 \cup_\rho \dots \cup_\rho \sigma_n$
for
$\sigma_1 \cup_\rho \dots \cup_\rho \sigma_n$
for
![]() $\sigma_1,\dots,\sigma_n \subseteq \rho$
.
$\sigma_1,\dots,\sigma_n \subseteq \rho$
.
A given call sequence may contain multiple identical subsequences. So it does not suffice to say “merge subsequences
![]() $ac.ac$
and
$ac.ac$
and
![]() $ad.bc$
of call sequence
$ad.bc$
of call sequence
![]() $ac.ad.ac.bc.ac$
,” as the latter contains three subsequences
$ac.ad.ac.bc.ac$
,” as the latter contains three subsequences
![]() $ac.ac$
. The definition above requires to select one of those three.
$ac.ac$
. The definition above requires to select one of those three.
Definition 1. Language. For a finite set of agents A, the language
![]() $\mathcal{L}$
is given by
$\mathcal{L}$
is given by
![]() $\varphi \ ::= \ b_a \mid \neg \varphi \mid \varphi \wedge \varphi \mid K_a \varphi$
where
$\varphi \ ::= \ b_a \mid \neg \varphi \mid \varphi \wedge \varphi \mid K_a \varphi$
where
![]() $a,b \in A$
. Let
$a,b \in A$
. Let
![]() $\to$
and
$\to$
and
![]() $\vee$
be defined as usual, and let
$\vee$
be defined as usual, and let
![]() $\hat{K}_a\varphi := \lnot K_a \lnot \varphi$
.
$\hat{K}_a\varphi := \lnot K_a \lnot \varphi$
.
The
![]() $\varphi$
are called formulas. The atomic formula
$\varphi$
are called formulas. The atomic formula
![]() $b_a$
reads as “agent a has the secret of b” or “agent a knows the secret of b.” The formula
$b_a$
reads as “agent a has the secret of b” or “agent a knows the secret of b.” The formula
![]() $K_a \varphi$
reads “agent a knows that
$K_a \varphi$
reads “agent a knows that
![]() $\varphi$
is true.”
$\varphi$
is true.”
Although we write “know” in “agent a knows the secret of b” and in “agent a knows that
![]() $\varphi$
is true”, the former is an atomic formula and only the second is an epistemic formula. In the former, we follow the convention in work on gossip.
$\varphi$
is true”, the former is an atomic formula and only the second is an epistemic formula. In the former, we follow the convention in work on gossip.
For
![]() $B \subseteq A$
, we define
$B \subseteq A$
, we define
![]() $E_B \varphi := \bigwedge_{a \in B} K_a \varphi$
and read it as “everyone in B knows that
$E_B \varphi := \bigwedge_{a \in B} K_a \varphi$
and read it as “everyone in B knows that
![]() $\varphi$
.” For
$\varphi$
.” For
![]() $E_A\varphi$
, we write
$E_A\varphi$
, we write
![]() $E \varphi$
. This is also known as shared or mutual knowledge (for B, for all) of
$E \varphi$
. This is also known as shared or mutual knowledge (for B, for all) of
![]() $\varphi$
.
$\varphi$
.
Agent a is an expert if she knows all the secrets, formally
![]() $\bigwedge_{b \in A} b_a$
, abbreviated as
$\bigwedge_{b \in A} b_a$
, abbreviated as
![]() $\mathit{Exp}_a$
. For
$\mathit{Exp}_a$
. For
![]() $B \subseteq A$
,
$B \subseteq A$
,
![]() $\mathit{Exp}_B := \bigwedge_{a\in B} \mathit{Exp}_a$
, for everyone in B is an expert, where
$\mathit{Exp}_B := \bigwedge_{a\in B} \mathit{Exp}_a$
, for everyone in B is an expert, where
![]() $\mathit{Exp}_A$
means that everyone is an expert. (We let
$\mathit{Exp}_A$
means that everyone is an expert. (We let
![]() $\mathit{Exp}_\emptyset$
mean
$\mathit{Exp}_\emptyset$
mean
![]() $\top$
.) Furthermore,
$\top$
.) Furthermore,
![]() $\mathit{NExp}_B := \bigwedge_{a \in B} \neg \mathit{Exp}_a$
, for everyone is B is a non-expert. Agent a is a super expert if she knows that everyone is an expert, formally
$\mathit{NExp}_B := \bigwedge_{a \in B} \neg \mathit{Exp}_a$
, for everyone is B is a non-expert. Agent a is a super expert if she knows that everyone is an expert, formally
![]() $K_a \mathit{Exp}_A$
. Therefore,
$K_a \mathit{Exp}_A$
. Therefore,
![]() $E\!\mathit{Exp}_A$
means that everyone is a super expert and
$E\!\mathit{Exp}_A$
means that everyone is a super expert and
![]() $E\!E\!\mathit{Exp}_A$
means that everyone knows that everyone is a super expert.
$E\!E\!\mathit{Exp}_A$
means that everyone knows that everyone is a super expert.
We slightly further generalize notation. Let non-empty
![]() $B,C \subseteq A$
. If all
$B,C \subseteq A$
. If all
![]() $a \in B$
know the secrets of all the agents in C, then we say that all B are C experts, denoted
$a \in B$
know the secrets of all the agents in C, then we say that all B are C experts, denoted
![]() $\mathit{Exp}_B(C)$
, where if
$\mathit{Exp}_B(C)$
, where if
![]() $C=A$
we omit the parameter C. If a knows that all the agents in B know the secrets of all the agents in B, a is a B super expert so that
$C=A$
we omit the parameter C. If a knows that all the agents in B know the secrets of all the agents in B, a is a B super expert so that
![]() $E_B\mathit{Exp}_B(B)$
denotes that all agents in B are B super experts.
$E_B\mathit{Exp}_B(B)$
denotes that all agents in B are B super experts.
The epistemic relation defined below models that agents only observe the calls they are involved in. In particular, there is no global clock and the conditions are asynchronous, meaning agents do not know how many calls have taken place.
Definitions Definition 2 and 3 are done by simultaneous induction on call sequences.
Definition 2. Epistemic relation. Let
![]() $a \in A$
. The epistemic relation
$a \in A$
. The epistemic relation
![]() $\sim_a$
is the smallest equivalence relation between call sequences such that:
$\sim_a$
is the smallest equivalence relation between call sequences such that:
-
 $\epsilon \sim_a \epsilon$
$\epsilon \sim_a \epsilon$
-
if
 $\sigma \sim_a \tau$
and
$\sigma \sim_a \tau$
and
 $a \notin \{b,c\}$
, then
$a \notin \{b,c\}$
, then
 $\sigma\kern-0.8pt{.}bc \sim_a \tau$
$\sigma\kern-0.8pt{.}bc \sim_a \tau$
-
if
 $\sigma \sim_a \tau$
, and for all c,
$\sigma \sim_a \tau$
, and for all c,
 $\sigma \models c_b$
iff
$\sigma \models c_b$
iff
 $\tau \models c_b$
, then
$\tau \models c_b$
, then
 $\sigma\kern-0.8pt{.}ab \sim_a \tau.ab$
$\sigma\kern-0.8pt{.}ab \sim_a \tau.ab$
As we assume the asynchronous cases, in the last clause of Definition 2, there are infinitely many such
![]() $\tau$
. This is not a problem for the formal semantics and our results here, but of course an issue for practical implementations – see also van Ditmarsch et al. (Reference van Ditmarsch, van der Hoek and Kuijer2020), Gattinger (Reference Gattinger2023).
$\tau$
. This is not a problem for the formal semantics and our results here, but of course an issue for practical implementations – see also van Ditmarsch et al. (Reference van Ditmarsch, van der Hoek and Kuijer2020), Gattinger (Reference Gattinger2023).
Definition 3. Semantics. Let call sequence
![]() $\sigma$
and formula
$\sigma$
and formula
![]() $\varphi \in \mathcal{L}$
be given. We define
$\varphi \in \mathcal{L}$
be given. We define
![]() $\sigma\models\varphi$
by induction on the structure of
$\sigma\models\varphi$
by induction on the structure of
![]() $\varphi$
. Moreover, we define the valuation of atoms by induction on
$\varphi$
. Moreover, we define the valuation of atoms by induction on
![]() $\sigma$
, for any
$\sigma$
, for any
![]() $a,b \in A$
:
$a,b \in A$
:

A formula
![]() $\varphi$
is valid, notation
$\varphi$
is valid, notation
![]() $\models\varphi$
, iff for all call sequences
$\models\varphi$
, iff for all call sequences
![]() $\sigma$
we have
$\sigma$
we have
![]() $\sigma\models\varphi$
. We abbreviate the set of secrets known by a after
$\sigma\models\varphi$
. We abbreviate the set of secrets known by a after
![]() $\sigma$
with
$\sigma$
with
![]() $a(\sigma) := \{c \in A \mid \sigma \models c_a\}$
.
$a(\sigma) := \{c \in A \mid \sigma \models c_a\}$
.
If in call ab agent a or b becomes an expert, then the other agent must also be an expert after this call. In contrast, if in a call ab agent a or b becomes a super expert, then the other agent does not have to become a super expert in this call.
4. Causal Relation and Causal Cone
We now introduce additional notation for specific subsequences of calls. The goal is to make it easy to select and reason about those calls that are relevant for a specific subset of agents.
Definition 4. Causal relation. For any sequence
![]() $\sigma$
and calls
$\sigma$
and calls
![]() $ab,cd \in \sigma$
, we write
$ab,cd \in \sigma$
, we write
![]() $ab < cd$
iff
$ab < cd$
iff
![]() $\sigma$
has shape
$\sigma$
has shape
![]() $\sigma_1.ab.\sigma_2.cd.\sigma_3$
(i.e., this occurrence of the call ab in
$\sigma_1.ab.\sigma_2.cd.\sigma_3$
(i.e., this occurrence of the call ab in
![]() $\sigma$
is before this occurrence of the call cd in
$\sigma$
is before this occurrence of the call cd in
![]() $\sigma$
). We define the relation
$\sigma$
). We define the relation
![]() $\ll_0$
over call occurrences in
$\ll_0$
over call occurrences in
![]() $\sigma$
by
$\sigma$
by
![]() $ab \ll_0 cd \ :\Leftrightarrow \ ab < cd \text{ and } \{a,b\} \cap \{c,d\} \neq \varnothing$
. Let
$ab \ll_0 cd \ :\Leftrightarrow \ ab < cd \text{ and } \{a,b\} \cap \{c,d\} \neq \varnothing$
. Let
![]() $\ll$
be the reflexive transitive closure of
$\ll$
be the reflexive transitive closure of
![]() $\ll_0$
. Calls ab and cd are causally related iff
$\ll_0$
. Calls ab and cd are causally related iff
![]() $ab \ll cd$
.
$ab \ll cd$
.
Definition 5. Causal cone. Given a call sequence
![]() $\sigma$
and a set of agents
$\sigma$
and a set of agents
![]() $B \subseteq A$
, the causal cone of
$B \subseteq A$
, the causal cone of
![]() $\sigma$
for the agents in B, denoted
$\sigma$
for the agents in B, denoted
![]() $\sigma_\ll^B$
, is defined by induction.
$\sigma_\ll^B$
, is defined by induction.
 \[ \begin{array}{lll} \epsilon_\ll^B &:= & \epsilon \\ \end{array} \hspace{4em} \begin{array}{lll} {(\sigma\kern-0.8pt{.}ab)}_\ll^B & := & \left\{ \begin{array}{ll} \sigma_\ll^{B \cup \{a,b\}}.ab & \text{if } a \in B \text{ or }b \in B \\ \sigma_\ll^B & \text{otherwise} \\ \end{array} \right. \end{array} \]
\[ \begin{array}{lll} \epsilon_\ll^B &:= & \epsilon \\ \end{array} \hspace{4em} \begin{array}{lll} {(\sigma\kern-0.8pt{.}ab)}_\ll^B & := & \left\{ \begin{array}{ll} \sigma_\ll^{B \cup \{a,b\}}.ab & \text{if } a \in B \text{ or }b \in B \\ \sigma_\ll^B & \text{otherwise} \\ \end{array} \right. \end{array} \]
For
![]() $\sigma_\ll^{\{a,b\}}$
we write
$\sigma_\ll^{\{a,b\}}$
we write
![]() $\sigma_\ll^{ab}$
, etc. Furthermore, we let
$\sigma_\ll^{ab}$
, etc. Furthermore, we let
![]() $\sigma_{\not\ll}^B$
be the complement of
$\sigma_{\not\ll}^B$
be the complement of
![]() $\sigma_\ll^B$
in
$\sigma_\ll^B$
in
![]() $\sigma$
.
$\sigma$
.
Intuitively, given a call sequence
![]() $\sigma\kern-0.8pt{.}ab$
, the sequence
$\sigma\kern-0.8pt{.}ab$
, the sequence
![]() $\sigma_\ll^{ab}$
is the subsequence of
$\sigma_\ll^{ab}$
is the subsequence of
![]() $\sigma$
of which all calls are causally related to the final call ab (it is the causal cone of agents a and b); in other words,
$\sigma$
of which all calls are causally related to the final call ab (it is the causal cone of agents a and b); in other words,
![]() $\sigma_\ll^{ab}$
is the subsequence consisting of all
$\sigma_\ll^{ab}$
is the subsequence consisting of all
![]() $cd \in \sigma$
such that
$cd \in \sigma$
such that
![]() $cd \ll ab$
in
$cd \ll ab$
in
![]() $\sigma\kern-0.8pt{.}ab$
. Also note that we can identify
$\sigma\kern-0.8pt{.}ab$
. Also note that we can identify
![]() $\sigma^a_\ll$
with the causal cone of the last call in
$\sigma^a_\ll$
with the causal cone of the last call in
![]() $\sigma$
involving a. In other words,
$\sigma$
involving a. In other words,
![]() $\sigma^a_\ll$
determines what a knows after
$\sigma^a_\ll$
determines what a knows after
![]() $\sigma$
.
$\sigma$
.
The complement
![]() $\sigma_{\not\ll}^B$
are the calls that do not determine what a knows after
$\sigma_{\not\ll}^B$
are the calls that do not determine what a knows after
![]() $\sigma$
. Sequence
$\sigma$
. Sequence
![]() $\sigma_{\not\ll}^B$
consists of all
$\sigma_{\not\ll}^B$
consists of all
![]() $cd \in \sigma$
that do not determine what any agent in B knows after
$cd \in \sigma$
that do not determine what any agent in B knows after
![]() $\sigma$
.
$\sigma$
.
Observe that
![]() $\sigma^\emptyset_\ll = \epsilon$
for all
$\sigma^\emptyset_\ll = \epsilon$
for all
![]() $\sigma$
.
$\sigma$
.
If there are two or three agents, all calls in a call sequence are causally related.
Lemma 6. Let call sequence
![]() $\sigma$
, group
$\sigma$
, group
![]() $B \subseteq A$
of agents, and agent
$B \subseteq A$
of agents, and agent
![]() $a \in B$
be given. Then (i)
$a \in B$
be given. Then (i)
![]() $\sigma \sim_a \sigma_\ll^B$
and also (ii)
$\sigma \sim_a \sigma_\ll^B$
and also (ii)
![]() $\sigma \sim_a \sigma_\ll^B.\sigma_{\not{\ll}}^B$
.
$\sigma \sim_a \sigma_\ll^B.\sigma_{\not{\ll}}^B$
.
Proof. We prove (i) by induction on the length of
![]() $\sigma$
. Note that we declared B and
$\sigma$
. Note that we declared B and
![]() $a \in B$
after
$a \in B$
after
![]() $\sigma$
; hence, these may occur differently in our inductive assumption.
$\sigma$
; hence, these may occur differently in our inductive assumption.
Case
![]() $\sigma=\epsilon$
. This is by definition as
$\sigma=\epsilon$
. This is by definition as
![]() $\epsilon_\ll^B = \epsilon$
.
$\epsilon_\ll^B = \epsilon$
.
Case
![]() $\sigma=\tau.ab$
. By the definition of
$\sigma=\tau.ab$
. By the definition of
![]() $\ll$
, we have
$\ll$
, we have
![]() ${(\tau.ab)}_\ll^B = \tau_\ll^{B+b}.ab$
(we recall that
${(\tau.ab)}_\ll^B = \tau_\ll^{B+b}.ab$
(we recall that
![]() $a \in B$
). By inductive assumption, we have
$a \in B$
). By inductive assumption, we have
![]() $\tau \sim_a \tau_\ll^{B+b}$
and also
$\tau \sim_a \tau_\ll^{B+b}$
and also
![]() $\tau \sim_b \tau_\ll^{B+b}$
so that agent b holds the same secrets after both. Therefore, by definition of
$\tau \sim_b \tau_\ll^{B+b}$
so that agent b holds the same secrets after both. Therefore, by definition of
![]() $\sim_a$
, we have
$\sim_a$
, we have
![]() $\tau.ab \sim_a \tau_\ll^{B+b}.ab$
. Combining this, we obtain
$\tau.ab \sim_a \tau_\ll^{B+b}.ab$
. Combining this, we obtain
![]() $\tau.ab \sim_a {(\tau.ab)}_\ll^B$
.
$\tau.ab \sim_a {(\tau.ab)}_\ll^B$
.
Case
![]() $\sigma=\tau.bc$
with
$\sigma=\tau.bc$
with
![]() $b,c \neq a$
and
$b,c \neq a$
and
![]() $b \in B$
or
$b \in B$
or
![]() $c \in B$
. By the definition of
$c \in B$
. By the definition of
![]() $\ll$
and because b or c is in B,
$\ll$
and because b or c is in B,
![]() ${(\tau.bc)}_\ll^B = \tau_\ll^{B+bc}.bc$
. By induction,
${(\tau.bc)}_\ll^B = \tau_\ll^{B+bc}.bc$
. By induction,
![]() $\tau \sim_a \tau^{B+bc}_\ll$
, and from that, the fact that
$\tau \sim_a \tau^{B+bc}_\ll$
, and from that, the fact that
![]() $b,c \neq a$
, and the definition of
$b,c \neq a$
, and the definition of
![]() $\sim_a$
, we also obtain
$\sim_a$
, we also obtain
![]() $\tau.bc \sim_a \tau^{B+bc}_\ll.bc$
and therefore
$\tau.bc \sim_a \tau^{B+bc}_\ll.bc$
and therefore
![]() $\tau.bc \sim_a {(\tau.bc)}_\ll^B$
.
$\tau.bc \sim_a {(\tau.bc)}_\ll^B$
.
Case
![]() $\sigma=\tau.bc$
with
$\sigma=\tau.bc$
with
![]() $b,c \notin B$
. We have that
$b,c \notin B$
. We have that
![]() $\tau.bc \sim_a \tau$
by the definition of
$\tau.bc \sim_a \tau$
by the definition of
![]() $\sim_a$
, because
$\sim_a$
, because
![]() $b,c \neq a$
. By inductive assumption,
$b,c \neq a$
. By inductive assumption,
![]() $\tau \sim_a \tau_\ll^B$
. By the definition of
$\tau \sim_a \tau_\ll^B$
. By the definition of
![]() $\ll$
and because
$\ll$
and because
![]() $b,c \neq a$
,
$b,c \neq a$
,
![]() $\tau_\ll^B = {(\tau.bc)}_\ll^B$
. Combining all this, we obtain
$\tau_\ll^B = {(\tau.bc)}_\ll^B$
. Combining all this, we obtain
![]() $\tau.bc \sim_a {(\tau.bc)}_\ll^B$
.
$\tau.bc \sim_a {(\tau.bc)}_\ll^B$
.
We now prove (ii). From
![]() $\sigma \sim_a \sigma_\ll^B$
, it follows that
$\sigma \sim_a \sigma_\ll^B$
, it follows that
![]() $\sigma \sim_a \sigma_\ll^B.\sigma_{\not\ll}^B$
by the definition of
$\sigma \sim_a \sigma_\ll^B.\sigma_{\not\ll}^B$
by the definition of
![]() $\sim_a$
and the observation that a does not occur in any call in
$\sim_a$
and the observation that a does not occur in any call in
![]() $\sigma_{\not\ll}^B$
.
$\sigma_{\not\ll}^B$
.
An instantiation of Lemma 6 is that
![]() $\sigma \sim_a \sigma_\ll^a.\sigma_{\not{\ll}}^a$
and
$\sigma \sim_a \sigma_\ll^a.\sigma_{\not{\ll}}^a$
and
![]() $\sigma \sim_a \sigma_\ll^a$
: a considers it possible that all not causally related calls, if any, take place after her last call.
$\sigma \sim_a \sigma_\ll^a$
: a considers it possible that all not causally related calls, if any, take place after her last call.
Moreover, note that we have
![]() ${(\sigma\kern-0.8pt{.}ab)}^{ab}_\ll = \sigma^{ab}_\ll.ab$
and
${(\sigma\kern-0.8pt{.}ab)}^{ab}_\ll = \sigma^{ab}_\ll.ab$
and
![]() ${(\sigma\kern-0.8pt{.}ab)}^{ab}_{\not\ll} = \sigma^{ab}_{\not\ll}$
by Definition 5. Hence, Lemma 6 also implies the following corollary.
${(\sigma\kern-0.8pt{.}ab)}^{ab}_{\not\ll} = \sigma^{ab}_{\not\ll}$
by Definition 5. Hence, Lemma 6 also implies the following corollary.
Corollary 7. Let call sequence
![]() $\sigma$
and call ab be given. Then
$\sigma$
and call ab be given. Then
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma_\ll^{ab}.ab.\sigma_{\not\ll}^{ab}$
and also
$\sigma\kern-0.8pt{.}ab \sim_a \sigma_\ll^{ab}.ab.\sigma_{\not\ll}^{ab}$
and also
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma_\ll^{ab}.ab$
.
$\sigma\kern-0.8pt{.}ab \sim_a \sigma_\ll^{ab}.ab$
.
Using the causal cone, we can show an elementary result about the limits of the knowledge of a non-expert. The result is obvious, but it it shown to dispel any doubt
Lemma 8. An agent who is not an expert cannot know that another agent is an expert.
Proof. Let
![]() $a \in A$
and call sequence
$a \in A$
and call sequence
![]() $\sigma$
be given and assume
$\sigma$
be given and assume
![]() $\sigma \not \models \mathit{Exp}_a$
. From Lemma 6, it follows that
$\sigma \not \models \mathit{Exp}_a$
. From Lemma 6, it follows that
![]() $\sigma \sim_a \sigma_\ll^a$
. Observe that for all agents
$\sigma \sim_a \sigma_\ll^a$
. Observe that for all agents
![]() $b \in A$
, if b occurs in a call in
$b \in A$
, if b occurs in a call in
![]() $\sigma_\ll$
, then
$\sigma_\ll$
, then
![]() $b(\sigma_\ll^a) \subseteq a(\sigma_\ll^a)$
, and if b does not occur in
$b(\sigma_\ll^a) \subseteq a(\sigma_\ll^a)$
, and if b does not occur in
![]() $\sigma_\ll^a$
, then
$\sigma_\ll^a$
, then
![]() $b(\sigma_\ll^a) = \{b\}$
: a considers it possible that b has not yet been involved in a call. Therefore, in the first case, given
$b(\sigma_\ll^a) = \{b\}$
: a considers it possible that b has not yet been involved in a call. Therefore, in the first case, given
![]() $a(\sigma_\ll^a) \subsetneq A$
also
$a(\sigma_\ll^a) \subsetneq A$
also
![]() $b(\sigma_\ll^a) \subsetneq A$
, whereas in the second case,
$b(\sigma_\ll^a) \subsetneq A$
, whereas in the second case,
![]() $\{b\} \subsetneq A$
. Either way
$\{b\} \subsetneq A$
. Either way
![]() $\sigma_\ll^a \not \models \mathit{Exp}_b$
. Therefore,
$\sigma_\ll^a \not \models \mathit{Exp}_b$
. Therefore,
![]() $\sigma \not \models K_a \mathit{Exp}_b$
.
$\sigma \not \models K_a \mathit{Exp}_b$
.
Slightly more general than Lemma 8, a non-expert cannot know that another agent holds more secrets than herself (even if that other agent is not an expert).
Somewhat related to causality, the following Lemma 9 shows that if agent a considers it possible that all agents in B are non-experts, then she considers a call sequence possible wherein all agents in B hold the same secrets as in the actual call sequence right before they became experts. In particular, for any agent in B that is not yet an expert, this means a considers their actual set of secrets possible.
For any call sequence
![]() $\sigma$
and agent b, let
$\sigma$
and agent b, let
![]() $\sigma^{<b}= \sigma$
whenever b is not an expert after
$\sigma^{<b}= \sigma$
whenever b is not an expert after
![]() $\sigma$
, and otherwise let
$\sigma$
, and otherwise let
![]() $\sigma^{<b}$
be the prefix of
$\sigma^{<b}$
be the prefix of
![]() $\sigma$
up to (and excluding) the call wherein b becomes an expert.
$\sigma$
up to (and excluding) the call wherein b becomes an expert.
Lemma 9. Let call sequence
![]() $\sigma$
,
$\sigma$
,
![]() $B \subseteq A$
and
$B \subseteq A$
and
![]() $a \in A$
be given. If
$a \in A$
be given. If
![]() $\sigma\models \hat{K}_a \mathit{NExp}_B$
, then there is a
$\sigma\models \hat{K}_a \mathit{NExp}_B$
, then there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
and for all
$\sigma\sim_a\tau$
and for all
![]() $b \in B$
,
$b \in B$
,
![]() $b(\sigma^{<b}) = b(\tau)$
.
$b(\sigma^{<b}) = b(\tau)$
.
Proof. The proof is by induction on the number of calls in
![]() $\sigma$
involving agent a. Note that if
$\sigma$
involving agent a. Note that if
![]() $b(\sigma^{<b}) = b(\tau)$
for all
$b(\sigma^{<b}) = b(\tau)$
for all
![]() $b \in B$
, then
$b \in B$
, then
![]() $\tau \models \mathit{NExp}_B$
.
$\tau \models \mathit{NExp}_B$
.
Basis Suppose agent a was not involved in any call in
![]() $\sigma$
. Let
$\sigma$
. Let
![]() $\tau = \bigcup_\sigma \{ b \in A \mid \sigma^{<b} \}$
. As agent a is not an expert, we have that
$\tau = \bigcup_\sigma \{ b \in A \mid \sigma^{<b} \}$
. As agent a is not an expert, we have that
![]() $\sigma\models \hat{K}_a \mathit{NExp}_A$
. As agent a does not occur in
$\sigma\models \hat{K}_a \mathit{NExp}_A$
. As agent a does not occur in
![]() $\sigma$
nor in
$\sigma$
nor in
![]() $\tau$
,
$\tau$
,
![]() $\sigma\sim_a\tau$
. By the definition of
$\sigma\sim_a\tau$
. By the definition of
![]() $\tau$
, for all
$\tau$
, for all
![]() $b \in A$
,
$b \in A$
,
![]() $b(\sigma^{<b}) = b(\tau)$
. In particular, this holds for all
$b(\sigma^{<b}) = b(\tau)$
. In particular, this holds for all
![]() $b \in B\subseteq A$
.
$b \in B\subseteq A$
.
Induction Let us now assume the property holds for
![]() $\sigma$
and let ac be the next call involving a. We distinguish cases by whether a and c were non-experts or experts before and after call ac.
$\sigma$
and let ac be the next call involving a. We distinguish cases by whether a and c were non-experts or experts before and after call ac.
Case agent a non-expert after call ac Let
![]() $\sigma\kern-0.8pt{.}ac\models\hat{K}_a\mathit{NExp}_B$
. In this case, we even have that
$\sigma\kern-0.8pt{.}ac\models\hat{K}_a\mathit{NExp}_B$
. In this case, we even have that
![]() $\sigma\kern-0.8pt{.}ac\models \hat{K}_a\mathit{NExp}_A$
and
$\sigma\kern-0.8pt{.}ac\models \hat{K}_a\mathit{NExp}_A$
and
![]() $\sigma\models \hat{K}_a\mathit{NExp}_A$
. By induction, there is a
$\sigma\models \hat{K}_a\mathit{NExp}_A$
. By induction, there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
and for all
$\sigma\sim_a\tau$
and for all
![]() $b \in A$
,
$b \in A$
,
![]() $b(\sigma^{<b}) = b(\tau)$
. From
$b(\sigma^{<b}) = b(\tau)$
. From
![]() $\sigma\sim_a\tau$
and
$\sigma\sim_a\tau$
and
![]() $c(\sigma^{<c})=c(\sigma)=c(\tau)$
, we obtain that
$c(\sigma^{<c})=c(\sigma)=c(\tau)$
, we obtain that
![]() $\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. After call ac,
$\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. After call ac,
![]() $a(\sigma\kern-0.8pt{.}ac)=c(\sigma\kern-0.8pt{.}ac)=c(\sigma)\cup a(\sigma)$
, and because
$a(\sigma\kern-0.8pt{.}ac)=c(\sigma\kern-0.8pt{.}ac)=c(\sigma)\cup a(\sigma)$
, and because
![]() $a(\sigma)=a(\tau)$
and
$a(\sigma)=a(\tau)$
and
![]() $c(\sigma)=c(\tau)$
, from that we also obtain
$c(\sigma)=c(\tau)$
, from that we also obtain
![]() $a(\sigma\kern-0.8pt{.}ac) = a(\tau.ac)$
and
$a(\sigma\kern-0.8pt{.}ac) = a(\tau.ac)$
and
![]() $c(\sigma\kern-0.8pt{.}ac) = c(\tau.ac)$
. Furthermore, for all
$c(\sigma\kern-0.8pt{.}ac) = c(\tau.ac)$
. Furthermore, for all
![]() $b \in A{-}ac$
, it follows from
$b \in A{-}ac$
, it follows from
![]() $b(\sigma^{<b}) = b(\tau)$
that
$b(\sigma^{<b}) = b(\tau)$
that
![]() $b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
. The requirement is therefore met for all agents in A and in particular for
$b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
. The requirement is therefore met for all agents in A and in particular for
![]() $B \subseteq A$
(it does not matter whether a or c are in B).
$B \subseteq A$
(it does not matter whether a or c are in B).
Case agent a expert before call ac Let
![]() $\sigma\kern-0.8pt{.}ac\models\hat{K}_a\mathit{NExp}_B$
. We distinguish the subcases where before call ac agent c was a non-expert, an expert known by a, and an expert unknown by a. In the latter two cases, we also refer to agent c as a known expert or unknown expert, respectively.
$\sigma\kern-0.8pt{.}ac\models\hat{K}_a\mathit{NExp}_B$
. We distinguish the subcases where before call ac agent c was a non-expert, an expert known by a, and an expert unknown by a. In the latter two cases, we also refer to agent c as a known expert or unknown expert, respectively.
If c was a non-expert, then
![]() $\sigma\models\hat{K}_a\mathit{NExp}_{B{+}c}$
, and therefore by induction there is a
$\sigma\models\hat{K}_a\mathit{NExp}_{B{+}c}$
, and therefore by induction there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
and for all
$\sigma\sim_a\tau$
and for all
![]() $b \in B{+}c$
,
$b \in B{+}c$
,
![]() $b(\sigma^{<b}) = b(\tau)$
. In particular,
$b(\sigma^{<b}) = b(\tau)$
. In particular,
![]() $c(\sigma^{<c}) = c(\sigma) = c(\tau)$
so that we also have
$c(\sigma^{<c}) = c(\sigma) = c(\tau)$
so that we also have
![]() $\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. As no
$\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. As no
![]() $b\in B$
is involved in the call ac, for all
$b\in B$
is involved in the call ac, for all
![]() $b \in B$
it remains the case that
$b \in B$
it remains the case that
![]() $b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
, as required.
Footnote 2
$b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
, as required.
Footnote 2
If c was a known expert (by a), the set B of agents that a considers possible to be non-experts need not change before and after call ac. Also,
![]() $\sigma\models\hat{K}_a\mathit{NExp}_B$
. From that, it follows by induction that there is a
$\sigma\models\hat{K}_a\mathit{NExp}_B$
. From that, it follows by induction that there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
and for all
$\sigma\sim_a\tau$
and for all
![]() $b \in B$
,
$b \in B$
,
![]() $b(\sigma^{<b}) = b(\tau)$
. As
$b(\sigma^{<b}) = b(\tau)$
. As
![]() $\sigma\sim_a\tau$
and
$\sigma\sim_a\tau$
and
![]() $c(\sigma) = c(\tau) = A$
, and also
$c(\sigma) = c(\tau) = A$
, and also
![]() $\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. As no
$\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. As no
![]() $b\in B$
is involved in the call ac, for all
$b\in B$
is involved in the call ac, for all
![]() $b \in B$
it remains the case that
$b \in B$
it remains the case that
![]() $b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
.
$b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
.
If c was an unknown expert (by a),
![]() $\sigma\models\hat{K}_a\mathit{NExp}_{B+c}$
, by induction there is a
$\sigma\models\hat{K}_a\mathit{NExp}_{B+c}$
, by induction there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
and for all
$\sigma\sim_a\tau$
and for all
![]() $b \in B{+}c$
,
$b \in B{+}c$
,
![]() $b(\sigma^{<b}) = b(\tau)$
so that
$b(\sigma^{<b}) = b(\tau)$
so that
![]() $c(\sigma^{<c}) \neq c(\sigma)$
. As a was already an expert after
$c(\sigma^{<c}) \neq c(\sigma)$
. As a was already an expert after
![]() $\sigma$
, there is a
$\sigma$
, there is a
![]() $d \neq a,c$
that a knows to be an expert. We now have that
$d \neq a,c$
that a knows to be an expert. We now have that
![]() $\sigma\kern-0.8pt{.}ac \sim_a \tau.cd.ac$
(from
$\sigma\kern-0.8pt{.}ac \sim_a \tau.cd.ac$
(from
![]() $\sigma\sim_a\tau$
and
$\sigma\sim_a\tau$
and
![]() $a\neq c,d$
we obtain
$a\neq c,d$
we obtain
![]() $\sigma\sim_a\tau.cd$
, and from that and
$\sigma\sim_a\tau.cd$
, and from that and
![]() $c(\sigma)=c(\tau.cd)=A$
we obtain
$c(\sigma)=c(\tau.cd)=A$
we obtain
![]() $\sigma\kern-0.8pt{.}ac \sim_a \tau.cd.ac$
). As no
$\sigma\kern-0.8pt{.}ac \sim_a \tau.cd.ac$
). As no
![]() $b\in B$
is involved in the calls cd and ac, for all
$b\in B$
is involved in the calls cd and ac, for all
![]() $b \in B$
, it remains the case that
$b \in B$
, it remains the case that
![]() $b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.cd.ac)$
.
$b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.cd.ac)$
.
Case agent a becomes expert in call ac Let
![]() $\sigma\kern-0.8pt{.}ac\models\hat{K}_a\mathit{NExp}_B$
. As
$\sigma\kern-0.8pt{.}ac\models\hat{K}_a\mathit{NExp}_B$
. As
![]() $\sigma\not\models \mathit{Exp}_a$
,
$\sigma\not\models \mathit{Exp}_a$
,
![]() $\sigma\models \hat{K}_a \mathit{NExp}_A$
. We distinguish the subcases where before call ac agent c was a non-expert, and an unknown expert (as a was not an expert after
$\sigma\models \hat{K}_a \mathit{NExp}_A$
. We distinguish the subcases where before call ac agent c was a non-expert, and an unknown expert (as a was not an expert after
![]() $\sigma$
, there is no case where c is known by a to be an expert).
$\sigma$
, there is no case where c is known by a to be an expert).
Let
![]() $\sigma\models \neg\mathit{Exp}_c$
. From
$\sigma\models \neg\mathit{Exp}_c$
. From
![]() $\sigma\models \hat{K}_a \mathit{NExp}_A$
, it follows by induction that there is a
$\sigma\models \hat{K}_a \mathit{NExp}_A$
, it follows by induction that there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
and for all
$\sigma\sim_a\tau$
and for all
![]() $b \in A$
,
$b \in A$
,
![]() $b(\sigma^{<b}) = b(\tau)$
. In particular,
$b(\sigma^{<b}) = b(\tau)$
. In particular,
![]() $c(\sigma^{<c}) = c(\sigma) = c(\tau)$
so that with
$c(\sigma^{<c}) = c(\sigma) = c(\tau)$
so that with
![]() $\sigma\sim_a\tau$
we also have
$\sigma\sim_a\tau$
we also have
![]() $\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. As no
$\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. As no
![]() $b\in B$
is involved in the call ac, for all
$b\in B$
is involved in the call ac, for all
![]() $b \in B$
it remains the case that
$b \in B$
it remains the case that
![]() $b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
.
$b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
.
Let now
![]() $\sigma\models \mathit{Exp}_c$
. As
$\sigma\models \mathit{Exp}_c$
. As
![]() $\sigma\models \hat{K}_a \mathit{NExp}_A$
, also
$\sigma\models \hat{K}_a \mathit{NExp}_A$
, also
![]() $\sigma\models \hat{K}_a \mathit{NExp}_B$
. It follows by induction that there is a
$\sigma\models \hat{K}_a \mathit{NExp}_B$
. It follows by induction that there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
and for all
$\sigma\sim_a\tau$
and for all
![]() $b \in B$
,
$b \in B$
,
![]() $b(\sigma^{<b}) = b(\tau)$
. From
$b(\sigma^{<b}) = b(\tau)$
. From
![]() $\sigma\sim_a\tau$
and
$\sigma\sim_a\tau$
and
![]() $c(\sigma) = c(\tau) = A$
, we obtain
$c(\sigma) = c(\tau) = A$
, we obtain
![]() $\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. As no
$\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. As no
![]() $b\in B$
is involved in the call ac, for all
$b\in B$
is involved in the call ac, for all
![]() $b \in B$
it remains the case that
$b \in B$
it remains the case that
![]() $b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
.
Footnote 3
$b({(\sigma\kern-0.8pt{.}ac)}^{<b}) = b(\tau.ac)$
.
Footnote 3
5. Lucky Calls
5.1 Introduction
In the introduction, we informally introduced the notion of a lucky call. We now make this notion precise. The goal of this section is to characterize when lucky calls can happen.
Definition 10. An agent a is lucky in a call ab if she learns in that call that another agent c is an expert. Formally, given all different agents
![]() $a,b,c \in A$
and a call sequence
$a,b,c \in A$
and a call sequence
![]() $\sigma$
, agent a is lucky about c in call ab iff
$\sigma$
, agent a is lucky about c in call ab iff
![]() $\sigma \not\models K_a \mathit{Exp}_c$
and
$\sigma \not\models K_a \mathit{Exp}_c$
and
![]() $\sigma\kern-0.8pt{.}ab \models K_a \mathit{Exp}_c$
.
$\sigma\kern-0.8pt{.}ab \models K_a \mathit{Exp}_c$
.
The characterization results in this section are obtained with combinatorial rather than logical means. Because the proofs are fairly long and the case distinctions multiple and even further refined, the section consists of different subsections in order to make it more accessible to the reader. Let us first provide an overview of these results.
In order to determine when an agent can be lucky in a call, we distinguish four cases: whether the caller is an expert and whether the callee is an expert. The case where the caller is an expert and the callee is a non-expert is the most complex case and is therefore distinguished in two subcases. Altogether the cases are exhaustive and mutually exclusive. Additionally, we provide several lemmas in order to show these cases. Having characterized all cases, we then show that an agent can only be lucky once. An overview of cases and results is in Table 4.
Table 4. Characterizing luck by mutually exclusive cases, given all different
![]() $a,b,c \in A$
, and call sequence
$a,b,c \in A$
, and call sequence
![]() $\sigma$
. Property
$\sigma$
. Property
![]() ${K_a\mathsf{magic}}$
is the formula
${K_a\mathsf{magic}}$
is the formula
![]() $K_a \bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a \mathit{Exp}_d)$
. Note that
$K_a \bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a \mathit{Exp}_d)$
. Note that
![]() $\sigma\not\models\mathit{Exp}_b$
already implies
$\sigma\not\models\mathit{Exp}_b$
already implies
![]() $\sigma\not\models K_a \mathit{Exp}_b$
. Technical condition
$\sigma\not\models K_a \mathit{Exp}_b$
. Technical condition
![]() $(*)$
is made explicit in Proposition 29
$(*)$
is made explicit in Proposition 29

In the cases where a is not an expert,
![]() $\sigma\not\models\mathit{Exp}_a$
, this already implies that
$\sigma\not\models\mathit{Exp}_a$
, this already implies that
![]() $\sigma\not\models K_a\mathit{Exp}_b$
by way of Lemma 8. We found it more elegant to keep both assumptions explicitly. The case where a and c are both experts comes logically last in the table but has results that are used in the case where a is an expert but not c. The former is therefore presented before the latter (the reader may have observed that 13
$\sigma\not\models K_a\mathit{Exp}_b$
by way of Lemma 8. We found it more elegant to keep both assumptions explicitly. The case where a and c are both experts comes logically last in the table but has results that are used in the case where a is an expert but not c. The former is therefore presented before the latter (the reader may have observed that 13
![]() $<$
29).
$<$
29).
5.2 Non-expert to non-expert
It is easy to show that when two non-experts call they cannot be lucky.
Proposition 11. Non-expert to non-expert. An agent who is not an expert and calling another non-expert is not lucky:
Let all different
![]() $a,b,c \in A$
and
$a,b,c \in A$
and
![]() $\sigma$
be given and suppose
$\sigma$
be given and suppose
![]() $\sigma \not\models \mathit{Exp}_a$
and
$\sigma \not\models \mathit{Exp}_a$
and
![]() $\sigma \not\models \mathit{Exp}_c$
. Then
$\sigma \not\models \mathit{Exp}_c$
. Then
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
Proof. From Corollary 7, it follows that
![]() $\sigma\kern-0.8pt{.}ac \sim_a \sigma_\ll^{ac}.ac$
. No call in
$\sigma\kern-0.8pt{.}ac \sim_a \sigma_\ll^{ac}.ac$
. No call in
![]() $\sigma_\ll^{ac}$
may contain an agent who is an expert, as the causal relation would then have made a or c an expert before call ac. Therefore,
$\sigma_\ll^{ac}$
may contain an agent who is an expert, as the causal relation would then have made a or c an expert before call ac. Therefore,
![]() $\sigma_\ll^{ac} \not\models \mathit{Exp}_b$
for all
$\sigma_\ll^{ac} \not\models \mathit{Exp}_b$
for all
![]() $b \in A$
other than a or c, and because of that and the semantics of calls also
$b \in A$
other than a or c, and because of that and the semantics of calls also
![]() $\sigma_\ll^{ac}.ac \not\models \mathit{Exp}_b$
. From that and
$\sigma_\ll^{ac}.ac \not\models \mathit{Exp}_b$
. From that and
![]() $\sigma\kern-0.8pt{.}ac \sim_a \sigma_\ll^{ac}.ac$
, it follows that
$\sigma\kern-0.8pt{.}ac \sim_a \sigma_\ll^{ac}.ac$
, it follows that
![]() $\sigma\kern-0.8pt{.}ac \models \neg K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \models \neg K_a \mathit{Exp}_b$
.
From Proposition 11, it follows in particular that when two agents both become experts in a call, they cannot be lucky. And as there are at least four agents, from that it then follows that neither agent becomes a super expert in that call. They both remain uncertain whether the two or more agents not involved in the call are experts.
5.3 Non-expert to expert
We now characterize the case where a non-expert is lucky when calling an expert.
Example 4. We recall the call sequence
![]() $ac.ad.ac.bc.ac$
from Example 2 (Table 2) wherein a’s final call ac is lucky: a learns that b and c are experts in that call.
$ac.ad.ac.bc.ac$
from Example 2 (Table 2) wherein a’s final call ac is lucky: a learns that b and c are experts in that call.
After the prefix
![]() $ac.ad.ac$
, a is a super expert for all agents but one (for
$ac.ad.ac$
, a is a super expert for all agents but one (for
![]() $\{a,c,d\}$
but not b): a knows that a,c,d know all the secrets of a,c,d. This allows a to learn in the final call ac that one of a,c,d must have called agent b and as it was not herself, c or d must have called b. Note that a does not learn that in fact c called b.
$\{a,c,d\}$
but not b): a knows that a,c,d know all the secrets of a,c,d. This allows a to learn in the final call ac that one of a,c,d must have called agent b and as it was not herself, c or d must have called b. Note that a does not learn that in fact c called b.
We now show that this typical case is also the only way for a non-expert to be lucky.
Proposition 12. Non-expert to expert. An agent who is not an expert is lucky iff she is a super expert for all agents but one and calls an expert among those:
Let all different
![]() $a,b,c \in A$
and
$a,b,c \in A$
and
![]() $\sigma$
be given and suppose
$\sigma$
be given and suppose
![]() $\sigma \not\models \mathit{Exp}_a$
and
$\sigma \not\models \mathit{Exp}_a$
and
![]() $\sigma \models \mathit{Exp}_c$
. Then
$\sigma \models \mathit{Exp}_c$
. Then
![]() $\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
iff
$\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
iff
![]() $\sigma \models K_a \mathit{Exp}_{A{-}b}(A{-}b)$
.
$\sigma \models K_a \mathit{Exp}_{A{-}b}(A{-}b)$
.
Proof. First note that
![]() $\sigma \not\models \mathit{Exp}_a$
implies
$\sigma \not\models \mathit{Exp}_a$
implies
![]() $\sigma \not\models K_a\mathit{Exp}_b$
(Lemma 8). Second, observe that
$\sigma \not\models K_a\mathit{Exp}_b$
(Lemma 8). Second, observe that
![]() $\sigma \models \mathit{Exp}_c$
implies
$\sigma \models \mathit{Exp}_c$
implies
![]() $\sigma\kern-0.8pt{.}ac \models \mathit{Exp}_a$
.
$\sigma\kern-0.8pt{.}ac \models \mathit{Exp}_a$
.
We now show the two directions.
![]() $(\Rightarrow)$
: We show the contrapositive: if a is not a
$(\Rightarrow)$
: We show the contrapositive: if a is not a
![]() $A{-}b$
super expert (
$A{-}b$
super expert (
![]() $\sigma \not\models K_a \mathit{Exp}_{A{-}b}(A{-}b)$
), then a cannot be lucky about b (i.e.,
$\sigma \not\models K_a \mathit{Exp}_{A{-}b}(A{-}b)$
), then a cannot be lucky about b (i.e.,
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
).
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
).
Intuitively, there are two ways in which non-expert a can be not a
![]() $A{-}b$
super expert: when she does not know enough or when she knows too much. In the first case, a does not know the secret of b but she is not a
$A{-}b$
super expert: when she does not know enough or when she knows too much. In the first case, a does not know the secret of b but she is not a
![]() $A{-}b$
super expert. In the second case, a knows the secret of b, as this is, in a way, “more” than being an
$A{-}b$
super expert. In the second case, a knows the secret of b, as this is, in a way, “more” than being an
![]() $A{-}b$
super expert who is not an expert, which implies ignorance of b.
$A{-}b$
super expert who is not an expert, which implies ignorance of b.
Case a does not know b. If
![]() $\sigma \models \lnot b_a$
, then a considers it possible that b has not yet made a call and thus only knows its own secret. In that case, as a is not a
$\sigma \models \lnot b_a$
, then a considers it possible that b has not yet made a call and thus only knows its own secret. In that case, as a is not a
![]() $A{-}b$
super expert, then a considers it possible that there is an agent
$A{-}b$
super expert, then a considers it possible that there is an agent
![]() $d \in A{-}b$
such that d does not know all of
$d \in A{-}b$
such that d does not know all of
![]() $A{-}b$
’s secrets, that is, then there is a
$A{-}b$
’s secrets, that is, then there is a
![]() $e \in A{-}b$
(where e may be a or c) such that d does not know the secret of e. Agent a thus considers it possible that the next two calls are
$e \in A{-}b$
(where e may be a or c) such that d does not know the secret of e. Agent a thus considers it possible that the next two calls are
![]() $db.dc$
and that b is not involved in further calls. After db, agent b is not an expert because neither b nor d know the secret of e. In dc, agent d informs c of the secret of b. This can still be followed by any call sequence
$db.dc$
and that b is not involved in further calls. After db, agent b is not an expert because neither b nor d know the secret of e. In dc, agent d informs c of the secret of b. This can still be followed by any call sequence
![]() $\tau$
of calls between the agents of
$\tau$
of calls between the agents of
![]() $A{-}ba$
making c expert before call ac. Altogether we get
$A{-}ba$
making c expert before call ac. Altogether we get
![]() $\sigma\kern-0.8pt{.}ac \sim_a \sigma\kern-0.8pt{.}db.dc.\tau.ac$
and
$\sigma\kern-0.8pt{.}ac \sim_a \sigma\kern-0.8pt{.}db.dc.\tau.ac$
and
![]() $\sigma\kern-0.8pt{.}db.dc.\tau.ac \not\models \mathit{Exp}_b$
. Therefore,
$\sigma\kern-0.8pt{.}db.dc.\tau.ac \not\models \mathit{Exp}_b$
. Therefore,
![]() $\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
.
Case a knows b. If
![]() $\sigma \models b_a$
, then a cannot also be a
$\sigma \models b_a$
, then a cannot also be a
![]() $A{-}b$
super expert as this implies that a also knows all other secrets and therefore is an expert, which contradicts our assumption. It remains to show that
$A{-}b$
super expert as this implies that a also knows all other secrets and therefore is an expert, which contradicts our assumption. It remains to show that
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
As non-expert a became expert in call ac, a learns a secret of some agent d in that call. As a already knew the secret of b, we must have
![]() $d \neq b$
.
$d \neq b$
.
First assume there is a last call in
![]() $\sigma$
between a and b. In that call ab, a therefore did not learn the secret of d. So after this call, a still considers it possible that d only knows its own secret.
$\sigma$
between a and b. In that call ab, a therefore did not learn the secret of d. So after this call, a still considers it possible that d only knows its own secret.
-
If after call ab agent a also knows the secret of c, then a considers it possible that c does not know d. If then the subsequent calls are
 $bc.cd$
and b was not involved in further calls, then after call bc agent b still does not know d, so b is not an expert. The part
$bc.cd$
and b was not involved in further calls, then after call bc agent b still does not know d, so b is not an expert. The part
 $bc.cd$
can still be followed by any sequence
$bc.cd$
can still be followed by any sequence
 $\tau$
of calls between the agents of
$\tau$
of calls between the agents of
 $A{-}ba$
making c expert before call ac. Altogether we get
$A{-}ba$
making c expert before call ac. Altogether we get
 $\sigma\kern-0.8pt{.}ac \sim_a \sigma\kern-0.8pt{.}bc.cd.\tau.ac$
and
$\sigma\kern-0.8pt{.}ac \sim_a \sigma\kern-0.8pt{.}bc.cd.\tau.ac$
and
 $\sigma\kern-0.8pt{.}bc.cd.\tau.ac \not\models \mathit{Exp}_b$
. Therefore,
$\sigma\kern-0.8pt{.}bc.cd.\tau.ac \not\models \mathit{Exp}_b$
. Therefore,
 $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
. -
If after call ab agent a does not know the secret of c, then b also does not know c, and a considers it possible that subsequently
 $bd.cd$
took place. After bd agent b is not an expert (because b still does not know c). Call cd informs c of the secret of b. This can still be followed by any number of calls between the agents of
$bd.cd$
took place. After bd agent b is not an expert (because b still does not know c). Call cd informs c of the secret of b. This can still be followed by any number of calls between the agents of
 $A{-}ba$
making c expert before call ac. Therefore,
$A{-}ba$
making c expert before call ac. Therefore,
 $\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
.
Second, assume there was no call in
![]() $\sigma$
between a and b. Then, given that a knows b and thus knows that a call took place between b and some agent e (where e may be c) in
$\sigma$
between a and b. Then, given that a knows b and thus knows that a call took place between b and some agent e (where e may be c) in
![]() $A{-}ba$
, we again conclude that b did not know d after that call nor after any call before the last call by a in
$A{-}ba$
, we again conclude that b did not know d after that call nor after any call before the last call by a in
![]() $\sigma$
(which happens to be the final call in
$\sigma$
(which happens to be the final call in
![]() $\sigma^a_\ll$
). Agent a considers a call sequence possible (with prefix
$\sigma^a_\ll$
). Agent a considers a call sequence possible (with prefix
![]() $\sigma^a_\ll$
) wherein after her last call b did not make further calls and that b’s secret was instead initially spread by agent e among the
$\sigma^a_\ll$
) wherein after her last call b did not make further calls and that b’s secret was instead initially spread by agent e among the
![]() $A{-}ba$
, and so on until c became expert. Therefore, also in this case,
$A{-}ba$
, and so on until c became expert. Therefore, also in this case,
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
![]() $(\Leftarrow)$
: Suppose
$(\Leftarrow)$
: Suppose
![]() $\sigma \models K_a\mathit{Exp}_{A{-}b}(A{-}b)$
. Note that we not only have
$\sigma \models K_a\mathit{Exp}_{A{-}b}(A{-}b)$
. Note that we not only have
![]() $\sigma\not\models\mathit{Exp}_a$
but also
$\sigma\not\models\mathit{Exp}_a$
but also
![]() $\sigma \models K_a \neg\mathit{Exp}_a$
. Moreover, we claim that
$\sigma \models K_a \neg\mathit{Exp}_a$
. Moreover, we claim that
![]() $\sigma \models \mathit{Exp}_c$
. To see this, note that after
$\sigma \models \mathit{Exp}_c$
. To see this, note that after
![]() $\sigma$
agent a is an
$\sigma$
agent a is an
![]() $A{-}b$
super expert, so a knows that c knows all secrets except b. Therefore, if a becomes expert in the last a call with c, then c must have learnt another secret. This can only be the secret of b. Therefore, a learnt that c was an expert after any
$A{-}b$
super expert, so a knows that c knows all secrets except b. Therefore, if a becomes expert in the last a call with c, then c must have learnt another secret. This can only be the secret of b. Therefore, a learnt that c was an expert after any
![]() $\tau \sim_a \sigma$
.
$\tau \sim_a \sigma$
.
In order to show
![]() $\sigma\kern-0.8pt{.}ac\models K_a \mathit{Exp}_b$
, let
$\sigma\kern-0.8pt{.}ac\models K_a \mathit{Exp}_b$
, let
![]() $\tau$
be arbitrary such that
$\tau$
be arbitrary such that
![]() $\tau.ac \sim_a \sigma\kern-0.8pt{.}ac$
. By definition of
$\tau.ac \sim_a \sigma\kern-0.8pt{.}ac$
. By definition of
![]() $\sim_a$
, we have
$\sim_a$
, we have
![]() $\tau\sim_a\sigma$
. From
$\tau\sim_a\sigma$
. From
![]() $\sigma \models\mathit{Exp}_c$
, we get
$\sigma \models\mathit{Exp}_c$
, we get
![]() $c(\tau) = c(\sigma) = A$
. It remains to show that
$c(\tau) = c(\sigma) = A$
. It remains to show that
![]() $\tau \models \mathit{Exp}_b$
. Also note that
$\tau \models \mathit{Exp}_b$
. Also note that
![]() $c(\tau) = A$
implies
$c(\tau) = A$
implies
![]() $\tau \models b_c$
.
$\tau \models b_c$
.
From
![]() $\tau\sim_a\sigma$
as well as
$\tau\sim_a\sigma$
as well as
![]() $\sigma \models K_a\mathit{Exp}_{A{-}b}(A{-}b)$
and
$\sigma \models K_a\mathit{Exp}_{A{-}b}(A{-}b)$
and
![]() $\sigma \models K_a\neg\mathit{Exp}_a$
, we get
$\sigma \models K_a\neg\mathit{Exp}_a$
, we get
![]() $\tau \models \mathit{Exp}_{A{-}b}(A{-}b)$
and
$\tau \models \mathit{Exp}_{A{-}b}(A{-}b)$
and
![]() $\tau\models \neg \mathit{Exp}_a$
.
$\tau\models \neg \mathit{Exp}_a$
.
These two imply that
![]() $\tau^a_\ll \models \neg b_d$
for any
$\tau^a_\ll \models \neg b_d$
for any
![]() $d \neq b$
(b does not occur in
$d \neq b$
(b does not occur in
![]() $\tau^a_\ll$
) and therefore in particular that
$\tau^a_\ll$
) and therefore in particular that
![]() $\tau^a_\ll \models \neg b_c$
.
$\tau^a_\ll \models \neg b_c$
.
From
![]() $\tau^a_\ll \models \neg b_c$
whereas
$\tau^a_\ll \models \neg b_c$
whereas
![]() $\tau\models b_c$
, it follows that
$\tau\models b_c$
, it follows that
![]() $\tau^a_{\not\ll}$
must contain a call bd involving b and some agent d where either
$\tau^a_{\not\ll}$
must contain a call bd involving b and some agent d where either
![]() $d=c$
or there is a subsequent call ce involving c (where
$d=c$
or there is a subsequent call ce involving c (where
![]() $d,e \neq a$
). Because
$d,e \neq a$
). Because
![]() $d({\tau^a_\ll}) = A{-}b$
for any such d, in the call bd agent b becomes an expert. (Also, ce explains how agent c became an expert.)
$d({\tau^a_\ll}) = A{-}b$
for any such d, in the call bd agent b becomes an expert. (Also, ce explains how agent c became an expert.)
Therefore,
![]() $\tau\models \mathit{Exp}_b$
, and as
$\tau\models \mathit{Exp}_b$
, and as
![]() $\tau$
was arbitrary such that
$\tau$
was arbitrary such that
![]() $\tau.ac\sim_a\sigma\kern-0.8pt{.}ac$
this shows that
$\tau.ac\sim_a\sigma\kern-0.8pt{.}ac$
this shows that
![]() $\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
.
Although we assume in Lemma 12 that there are at least four agents, it also holds for three agents.
Example 5. Consider three agents a, b, and c. In call sequence
![]() $ac.bc.ac$
, the third call is lucky and a then learns that c and b are experts. In the first call, a becomes a
$ac.bc.ac$
, the third call is lucky and a then learns that c and b are experts. In the first call, a becomes a
![]() $\{a,c\}$
super expert. In the second call ac, agent a learns that c must have called b and thus learns that b and c are experts and thus becomes a
$\{a,c\}$
super expert. In the second call ac, agent a learns that c must have called b and thus learns that b and c are experts and thus becomes a
![]() $\{a,b,c\}$
super expert.
$\{a,b,c\}$
super expert.
We can conclude from Lemma 12 that if
![]() $\sigma \models E_{A{-}b}\mathit{Exp}_{A{-}b}(A{-}b)$
, so when all agents in
$\sigma \models E_{A{-}b}\mathit{Exp}_{A{-}b}(A{-}b)$
, so when all agents in
![]() $A{-}b$
are
$A{-}b$
are
![]() $A{-}b$
super experts, and if also no agent in
$A{-}b$
super experts, and if also no agent in
![]() $A{-}b$
is an expert, all but one of those can be lucky in the same call sequence. To see this, after
$A{-}b$
is an expert, all but one of those can be lucky in the same call sequence. To see this, after
![]() $\sigma$
let some agent c call b. Let now all agents in
$\sigma$
let some agent c call b. Let now all agents in
![]() $A{-}bc$
call c. Then they all also learn in that call that b is an expert. Given
$A{-}bc$
call c. Then they all also learn in that call that b is an expert. Given
![]() $|A|=n$
agents, we therefore get
$|A|=n$
agents, we therefore get
![]() $n-2$
many lucky calls.
$n-2$
many lucky calls.
Example 6. With four agents we can have two lucky calls by non-experts. Recall
![]() $ac.ad.ac.bc.ac$
from Example 2 wherein a learns that b and c are experts in the final call ac. Now consider the expanded sequence
$ac.ad.ac.bc.ac$
from Example 2 wherein a learns that b and c are experts in the final call ac. Now consider the expanded sequence
![]() $ac.ad.ac.cd.bc.ac.cd$
: after
$ac.ad.ac.cd.bc.ac.cd$
: after
![]() $ac.ad.ac.cd$
, all of a,c,d know that all of a,c,d know all secrets of a,c,d. In penultimate call ac, a learns that b and c are experts, and in final call cd, d learns that b and c are experts.
$ac.ad.ac.cd$
, all of a,c,d know that all of a,c,d know all secrets of a,c,d. In penultimate call ac, a learns that b and c are experts, and in final call cd, d learns that b and c are experts.
Similarly, with 1000 agents we can have 998 lucky calls by non-experts.
5.4 Expert to expert
We now deal with calls between two experts and will show that they cannot be lucky. In the later Sections 5.5–5.7, we then consider calls between experts and non-experts, where we will show that the expert can be lucky. We investigate expert-to-expert calls first because they are easier and because we use results about them to prove our results for expert-to-non-expert calls.
Proposition 13. Expert to expert. An agent who is an expert and who calls another expert is not lucky:
Let all different
![]() $a,b,c \in A$
and
$a,b,c \in A$
and
![]() $\sigma$
be given and suppose
$\sigma$
be given and suppose
![]() $\sigma \models \mathit{Exp}_a$
,
$\sigma \models \mathit{Exp}_a$
,
![]() $\sigma \models \mathit{Exp}_c$
, and
$\sigma \models \mathit{Exp}_c$
, and
![]() $\sigma \not \models K_a\mathit{Exp}_b$
. Then
$\sigma \not \models K_a\mathit{Exp}_b$
. Then
![]() $\sigma\kern-0.8pt{.}ac \not \models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \not \models K_a \mathit{Exp}_b$
.
Proof. As
![]() $\sigma \models \mathit{Exp}_a$
, there must have been a call in
$\sigma \models \mathit{Exp}_a$
, there must have been a call in
![]() $\sigma$
wherein a became expert. Let
$\sigma$
wherein a became expert. Let
![]() $\sigma = \tau.ad.\rho$
where in call ad agent a became expert. As
$\sigma = \tau.ad.\rho$
where in call ad agent a became expert. As
![]() $\sigma \not\models K_a \mathit{Exp}_b$
,
$\sigma \not\models K_a \mathit{Exp}_b$
,
![]() $d \neq b$
.
$d \neq b$
.
The proof is by induction on the number m of calls involving a in subsequence
![]() $\rho$
.
$\rho$
.
(
![]() $m=0$
) We distinguish case
$m=0$
) We distinguish case
![]() $d=c$
from case
$d=c$
from case
![]() $d \neq c$
.
$d \neq c$
.
![]() $(d=c)$
From
$(d=c)$
From
![]() $\sigma \not\models K_a \mathit{Exp}_b$
, that is,
$\sigma \not\models K_a \mathit{Exp}_b$
, that is,
![]() $\tau.ac.\rho \not \models K_a \mathit{Exp}_b$
, it follows that there is
$\tau.ac.\rho \not \models K_a \mathit{Exp}_b$
, it follows that there is
![]() $\sigma'$
such that
$\sigma'$
such that
![]() $\tau.ac.\rho \sim_a \sigma'$
and
$\tau.ac.\rho \sim_a \sigma'$
and
![]() $\sigma' \not \models \mathit{Exp}_b$
. As
$\sigma' \not \models \mathit{Exp}_b$
. As
![]() $\tau.ac.\rho \sim_a \tau.ac$
(as a is not involved in a call in
$\tau.ac.\rho \sim_a \tau.ac$
(as a is not involved in a call in
![]() $\rho$
), also
$\rho$
), also
![]() $\tau.ac \sim_a \sigma'$
and we can assume that
$\tau.ac \sim_a \sigma'$
and we can assume that
![]() $\sigma'$
has shape
$\sigma'$
has shape
![]() $\tau'.ac$
where
$\tau'.ac$
where
![]() $\tau \sim_a \tau'$
, so that
$\tau \sim_a \tau'$
, so that
![]() $\tau.ac.\rho \sim_a \tau'.ac$
. From
$\tau.ac.\rho \sim_a \tau'.ac$
. From
![]() $\tau.ac.\rho \sim_a \tau'.ac$
and
$\tau.ac.\rho \sim_a \tau'.ac$
and
![]() $c(\tau.ac.\rho) =c(\tau'.ac) = A$
, we obtain that
$c(\tau.ac.\rho) =c(\tau'.ac) = A$
, we obtain that
![]() $\sigma\kern-0.8pt{.}ac = \tau.ac.\rho.ac \sim_a \tau'.ac.ac$
. As
$\sigma\kern-0.8pt{.}ac = \tau.ac.\rho.ac \sim_a \tau'.ac.ac$
. As
![]() $\tau'.ac \not \models \mathit{Exp}_b$
, also
$\tau'.ac \not \models \mathit{Exp}_b$
, also
![]() $\tau'.ac.ac \not \models \mathit{Exp}_b$
, so that
$\tau'.ac.ac \not \models \mathit{Exp}_b$
, so that
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
![]() $(d \neq c)$
In this, case
$(d \neq c)$
In this, case
![]() $\sigma\kern-0.8pt{.}ac = \tau.ad.\rho.ac$
. We obtain similarly to the previous case that there is
$\sigma\kern-0.8pt{.}ac = \tau.ad.\rho.ac$
. We obtain similarly to the previous case that there is
![]() $\tau' \sim_a \tau$
such that
$\tau' \sim_a \tau$
such that
![]() $\tau.ad \sim_a \tau'.ad$
and
$\tau.ad \sim_a \tau'.ad$
and
![]() $\tau'.ad\not\models \mathit{Exp}_b$
. It then follows that
$\tau'.ad\not\models \mathit{Exp}_b$
. It then follows that
![]() $\tau'.ad.cd.ac\not\models \mathit{Exp}_b$
, where
$\tau'.ad.cd.ac\not\models \mathit{Exp}_b$
, where
![]() $\sigma\kern-0.8pt{.}ac = \tau.ad.\rho.ac \sim_a \tau'.ad.cd.ac$
so that again
$\sigma\kern-0.8pt{.}ac = \tau.ad.\rho.ac \sim_a \tau'.ad.cd.ac$
so that again
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
. In other words, agent a considers it possible that c called d immediately after ad and that a then called c immediately after that. As neither call involved b, this does not affect what secrets are known by b, who therefore still is not an expert.
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
. In other words, agent a considers it possible that c called d immediately after ad and that a then called c immediately after that. As neither call involved b, this does not affect what secrets are known by b, who therefore still is not an expert.
(
![]() $m \geq 1$
) We now have that
$m \geq 1$
) We now have that
![]() $\sigma = \tau.ad.\rho_1.ae.\rho_2$
, where a is not involved in a call in
$\sigma = \tau.ad.\rho_1.ae.\rho_2$
, where a is not involved in a call in
![]() $\rho_2$
and where we may assume by induction that
$\rho_2$
and where we may assume by induction that
![]() $\tau.ad.\rho_1.ae \not\models K_a \mathit{Exp}_b$
, from which it follows that
$\tau.ad.\rho_1.ae \not\models K_a \mathit{Exp}_b$
, from which it follows that
![]() $e \neq b$
. We obtain similarly to the previous case that
$e \neq b$
. We obtain similarly to the previous case that
![]() $\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
, because a considers it possible that no calls took place after that call ae, in case
$\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
, because a considers it possible that no calls took place after that call ae, in case
![]() $e=c$
; or that only call ce took place after that call ae, in case
$e=c$
; or that only call ce took place after that call ae, in case
![]() $e \neq c$
.
$e \neq c$
.
5.5 Expert to non-expert – preliminaries
We proceed by investigating when experts can be lucky. This will be surprisingly more complex than the other cases. In this preparatory subsection, we introduce more terminology for calls and several detailed examples in order to provide the reader with intuitive guidance. The characterization of lucky experts and proofs are then in the following subsections.
In Example 3 (p. 2) analyzing call sequence
![]() $ab.cd.bd.ad.ac$
, before a was lucky in the final call ac, she became an expert in call ad by calling an agent who already was an expert. This is a necessary condition for any call sequence wherein an expert a is later to be lucky. Such a call is called a magic call, and the property thus obtained is called magic (for agent a).
$ab.cd.bd.ad.ac$
, before a was lucky in the final call ac, she became an expert in call ad by calling an agent who already was an expert. This is a necessary condition for any call sequence wherein an expert a is later to be lucky. Such a call is called a magic call, and the property thus obtained is called magic (for agent a).
Intuitively, magic means that a knows that some agent is an expert of which a does not know that it is an expert. Formally, we define it as follows.
Definition 14. Magic call, magic property. Let unequal
![]() $a,b \in A$
and a call sequence
$a,b \in A$
and a call sequence
![]() $\sigma$
be given. The magic property for a is the formula
$\sigma$
be given. The magic property for a is the formula
![]() ${K_a\mathsf{magic}} := K_a \bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a \mathit{Exp}_d)$
. Consider the call sequence
${K_a\mathsf{magic}} := K_a \bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a \mathit{Exp}_d)$
. Consider the call sequence
![]() $\sigma\kern-0.8pt{.}ab$
. If we have
$\sigma\kern-0.8pt{.}ab$
. If we have
![]() $\sigma\not\models\mathit{Exp}_a$
,
$\sigma\not\models\mathit{Exp}_a$
,
![]() $\sigma\models\mathit{Exp}_b$
, and call ab is not lucky, then we say that ab is a magic call.
$\sigma\models\mathit{Exp}_b$
, and call ab is not lucky, then we say that ab is a magic call.
Lemma 15. If call ab is magic in
![]() $\sigma\kern-0.8pt{.}ab$
, then: (i)
$\sigma\kern-0.8pt{.}ab$
, then: (i)
![]() $\sigma\kern-0.8pt{.}ab\models\mathit{Exp}_a$
, (ii)
$\sigma\kern-0.8pt{.}ab\models\mathit{Exp}_a$
, (ii)
![]() $\sigma\not\models{K_a\mathsf{magic}}$
, and (iii)
$\sigma\not\models{K_a\mathsf{magic}}$
, and (iii)
![]() $\sigma\kern-0.8pt{.}ab\models{K_a\mathsf{magic}}$
.
$\sigma\kern-0.8pt{.}ab\models{K_a\mathsf{magic}}$
.
Proof. (i): If a non-expert a calls an expert, then a is an expert after that call. (ii): The magic property states that any call sequence considered possible by agent a contains an expert. However, a non-expert considers it possible that all agents are non-experts (see Corollary 7, and Lemma 8 including its generalization): this follows from
![]() $\sigma\not\models\mathit{Exp}_a$
(so that
$\sigma\not\models\mathit{Exp}_a$
(so that
![]() $a(\sigma) \subsetneq A$
),
$a(\sigma) \subsetneq A$
),
![]() $\sigma \sim_a \sigma^a_\ll$
(so that also
$\sigma \sim_a \sigma^a_\ll$
(so that also
![]() $a(\sigma^a_\ll) \subsetneq A$
), and
$a(\sigma^a_\ll) \subsetneq A$
), and
![]() $c(\sigma^a_\ll) \subseteq a(\sigma^a_\ll)$
for all agents
$c(\sigma^a_\ll) \subseteq a(\sigma^a_\ll)$
for all agents
![]() $c\neq a$
(so that
$c\neq a$
(so that
![]() $c(\sigma^a_\ll) \subsetneq A$
for all
$c(\sigma^a_\ll) \subsetneq A$
for all
![]() $c \in A$
). Therefore, a cannot know that there is an expert; thus, magic cannot hold. (iii): In call ab, agent a learns that b was an expert before the call. Any call sequence considered possible by agent a must therefore contain a call wherein b and another agent both became experts. As a was not lucky in call ab, she does not know who that agent was.
$c \in A$
). Therefore, a cannot know that there is an expert; thus, magic cannot hold. (iii): In call ab, agent a learns that b was an expert before the call. Any call sequence considered possible by agent a must therefore contain a call wherein b and another agent both became experts. As a was not lucky in call ab, she does not know who that agent was.
In other words, a magic call for a is a call in which
![]() ${K_a\mathsf{magic}}$
becomes true, and it is a call that creates magic. Apart from wordplay, let us explain by way of typical examples what is magical about magic calls.
${K_a\mathsf{magic}}$
becomes true, and it is a call that creates magic. Apart from wordplay, let us explain by way of typical examples what is magical about magic calls.
Example 7. We recall Example 3 (Table 3) for the four agents a,b,c,d and the call sequence
![]() $ab.cd.bd.ad.ac$
. Call ad is a magic call wherein a becomes an expert and d already is an expert.
$ab.cd.bd.ad.ac$
. Call ad is a magic call wherein a becomes an expert and d already is an expert.
Before call ad, a was not an expert and therefore considers it possible that all other agents are also not experts. Therefore, after call ad, agent a knows that three agents are experts, namely herself, agent d, and the agent involved in the call with d making d an expert. However, a is uncertain whether b or c are experts. In the final call ac, agent a finds out that c was not an expert. Therefore, she learns that b is an expert. Therefore, the last call is lucky.
If the final call had been ab instead of ac, agent a would have learnt that b already was an expert and would therefore still have been uncertain whether c is an expert. A further call ac would have been necessary to determine that. So she would then not be lucky. Luck is never guaranteed.
After a magic call for agent a, the magic property implies that a knows that there is one more expert agent than she knows about. This can also be described in familiar “de re”/“de dicto” terms (Jamroga and van der Hoek Reference Jamroga and van der Hoek2004). After a magic call, agent a knows “de dicto” that there are three experts, that is, a knows that there are three agents that are experts. Whereas a only knows “de re” that there are two experts (and does not know “de re” that there are three experts); in other words, there are two agents such that a knows that they are experts (and there are no three agents such that a knows that they are experts). The magic property implies that the agent knows more experts “de dicto” than “de re.”
The lucky call need not be straight after the magic call. In Example 7, the next call can be a lucky call because there are only four agents. In general, this can take much longer. As long as magic is preserved, there is some
![]() $m<n$
such that a knows “de dicto” but not “de re” that there are
$m<n$
such that a knows “de dicto” but not “de re” that there are
![]() $m<n$
agents who are experts, and luck may happen when
$m<n$
agents who are experts, and luck may happen when
![]() $m=n-1$
.
$m=n-1$
.
Example 8. Let there be 1000 agents including a,b,c,d and assume that a becomes an expert in a call ad to an expert d, wherein she is not lucky, so that it is a magic call. Agent a now knows (de dicto) that there are three experts but only knows (de re) of two, namely a and d. Let now a after call ad call 996 non-experts. After the 996th of those calls a knows that there are 999 experts but only knows of 998. Suppose that at this stage she is still uncertain whether b and c are experts but knows that they cannot both be non-experts. Then, if a’s next, 997th, call is ac and a then observes that c is not an expert, she learns in that lucky call that b must be an expert. Again, a now is a super expert.
What if after a magic call for a she calls an expert before she is lucky? If a already knew this agent to be an expert (we will call this agent a known expert), then this call is not informative and magic is then not lost. However, if after a magic call agent a calls an agent she did not yet know to be an expert, then this almost always rules out that a can be lucky ever after. A simple example was the alternative call ab in Example 7 to an expert b. Five agents allow more interesting scenarios.
Example 9. Consider five agents a,b,c,d,e, and call sequence
![]() $ab.cd.bd.de$
. After this, agents d and e are experts, and a,b,c are non-experts.
$ab.cd.bd.de$
. After this, agents d and e are experts, and a,b,c are non-experts.
Let now call ae happen. This is a magic call. After this call agent a is still uncertain whether b,c,d are experts.
Any call involving a can now take place: if again call ae is the next call, then this is not informative, and magic is preserved; if the next call is ab, then a remains uncertain whether c and d are experts, and magic is preserved; if the next call is ac, then this is similar to a next call ab only now a remains uncertain whether b and d are experts; however if the next call is ad, agent a learns that d was an expert, and she now knows that there are three experts and considers possible that the remaining agents b,c are all non-experts. Magic is therefore lost.
The calls preserving magic affect each other in the following sense. Suppose the next call is ab, that is, consider the sequence
![]() $ab.cd.bd.de.ae.ab$
. Then subsequent calls ab,ae would not be informative, and call ad would still kill the magic, but call ac would now be lucky.
$ab.cd.bd.de.ae.ab$
. Then subsequent calls ab,ae would not be informative, and call ad would still kill the magic, but call ac would now be lucky.
It is also easy to see that once magic is lost, it is lost forever. For example, after
![]() $ab.cd.bd.de.ae.ad$
, if a subsequently calls an expert, either this is a known expert, or, if it is an unknown expert, she considers it possible that this agent was made an expert by e after call ae. This does not bring magic back. Whereas if a subsequently calls a non-expert, b or c, that agent could have obtained those secrets before call ad when nobody was an expert (as shown later).
$ab.cd.bd.de.ae.ad$
, if a subsequently calls an expert, either this is a known expert, or, if it is an unknown expert, she considers it possible that this agent was made an expert by e after call ae. This does not bring magic back. Whereas if a subsequently calls a non-expert, b or c, that agent could have obtained those secrets before call ad when nobody was an expert (as shown later).
Let us now continue on the lead suggested by “almost always.” Interestingly enough, magic is not always lost when subsequently to a magic call wherein an agent becomes an expert, that agent later calls an expert.
Example 10. Consider five agents a,b,c,d,e, and call sequence
![]() $bc.cd.bc.ab.ac.ce.ac.be.ab.ad$
. We show the results in Table 5.
$bc.cd.bc.ab.ac.ce.ac.be.ab.ad$
. We show the results in Table 5.
Table 5. Results of
![]() $bc.cd.bc.ab.ac.ce.ac.be.ab.ad$
, followed by the results of the shorter sequence
$bc.cd.bc.ab.ac.ce.ac.be.ab.ad$
, followed by the results of the shorter sequence
![]() $bc.cd.bc.ab.ac.ce.ac.ad$
where we only showed the final two rows, for comparison. Both sequences are the same until the horizontal line
$bc.cd.bc.ab.ac.ce.ac.ad$
where we only showed the final two rows, for comparison. Both sequences are the same until the horizontal line

After the first occurrence of call ac, agent a knows that agents b and c (and therefore also agent a herself) know all secrets except e. In call ce agent c becomes an expert, and in the second occurrence of call ac agent a learns that c is an expert: this is a magic call. The second call ab is a call between experts. Agent a can now reason as follows:
Can it be that agent b was the agent who made agent c an expert? I know that they both already knew all secrets except e before I became an expert. If they only knew that, then they would not become experts when calling each other.
The only way for b to make c an expert is that b learns the secret of e, which could have happened in two ways. (i) If b called e, then b and e both became experts so then after call bc there were already three experts, namely b,c,e, before I called c. (ii) If b learned e’s secret by e calling d, after which e and d remained non-experts, followed by call bd, then there are once again three experts, namely b,c,d before I called c. Therefore, apart from b, c and myself, one of d or e must also be an expert, but I do not know which one.
So magic is preserved after calling an expert. The last call, ad, is a lucky call. Agent a is now a super expert.
Similarly, if there are 1000 agents, it may happen that agent a knows that all agents except two know all secrets except the secret of one of those two, that one of those 997 then becomes expert and after that calls a in a lucky call. If a then keeps calling the remaining 996 such agents and keeps finding out that they are experts in such calls, then she can still be lucky in the end about one of those two agents (as shown later).
The final two rows of Table 5 show the execution of
![]() $bc.cd.bc.ab.ac.ce.ac.ad$
(where it differs from the execution of
$bc.cd.bc.ab.ac.ce.ac.ad$
(where it differs from the execution of
![]() $bc.cd.bc.ab.ac.ce.ac.be.ab.ad$
). In call ad, agent a is lucky about e. This is because a learns in that call:
$bc.cd.bc.ab.ac.ce.ac.be.ab.ad$
). In call ad, agent a is lucky about e. This is because a learns in that call:
Agent d does not know the secret of e; therefore, d and e did not call each other. Agent d is not an expert, so b or e must have made c an expert. If b made c an expert, then e must also be an expert (and b cannot have learnt e’s secret earlier, from d), whereas if e made c an expert, then b need not be an expert. Either way, a learns that e is an expert.
Observe that a is not yet a super expert and that b is not an expert. Indeed, we will show that an expert a can be lucky at any stage.
We find the phenomenon described in Example 10 a surprising exception to the usual loss of magic in a call between experts. Given a magic call ac an agent b is close if prior to the magic call agent a knows that a, b, and c are experts for all agents except one. Call ab above where b is close and is an unknown expert to a preserves magic.
Definition 16. Known expert, unknown expert, close, distant. Let
![]() $a,b,c \in A$
be all different agents and consider a call sequence
$a,b,c \in A$
be all different agents and consider a call sequence
![]() $\sigma\kern-0.8pt{.}ac.\tau.ab$
where ac is a magic call for a and such that
$\sigma\kern-0.8pt{.}ac.\tau.ab$
where ac is a magic call for a and such that
![]() $\sigma\kern-0.8pt{.}ac.\tau \models \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac.\tau \models \mathit{Exp}_b$
.
If
![]() $\sigma\kern-0.8pt{.}ac.\tau \models K_a\mathit{Exp}_b$
, then b is a known expert (to a) in call ac, and otherwise b is an unknown expert.
$\sigma\kern-0.8pt{.}ac.\tau \models K_a\mathit{Exp}_b$
, then b is a known expert (to a) in call ac, and otherwise b is an unknown expert.
f there is a
![]() $d \in A$
such that a knows that b knows all secrets except that of d, then the agents in the set
$d \in A$
such that a knows that b knows all secrets except that of d, then the agents in the set
![]() $C = \{ c \in A \mid \sigma \models K_a \mathit{Exp}_c(A{-}d)\}$
are called close (to being an expert) and the agents in
$C = \{ c \in A \mid \sigma \models K_a \mathit{Exp}_c(A{-}d)\}$
are called close (to being an expert) and the agents in
![]() $A{\setminus}C$
distant.
$A{\setminus}C$
distant.
We also apply the same terminology to call sequences extending
![]() $\sigma\kern-0.8pt{.}ac$
.
$\sigma\kern-0.8pt{.}ac$
.
We note that an agent c can only be close or distant with respect to three agents with their roles given in Definition 16: a knows that b knows all secrets except that of d. If the set of close agents C is empty, everyone is distant. If C is nonempty and b is close, then a must also be close (because all secrets known by b are also known by a) and d must be distant (because otherwise,
![]() $\mathit{Exp}_d(A-d)$
means that d must be an expert, as d always knows it own secret, and therefore a would also be an expert).
$\mathit{Exp}_d(A-d)$
means that d must be an expert, as d always knows it own secret, and therefore a would also be an expert).
Let us summarize what may be going on before an agent who is an expert becomes lucky. If following a magic call for agent a she calls a non-expert, a known expert, or an unknown close expert (a close call), magic is preserved and she can still eventually be lucky. Whereas whenever she calls an unknown distant expert (a distant call), she can no longer eventually be lucky. If agent a knows that there is at most one distant non-expert but is uncertain between two, then if she receives a call from the non-expert between them, she learns that the other agent she was uncertain about is an expert: she is lucky.
We now proceed to prove all this.
5.6 Expert to non-expert – without magic
We first show that once magic is lost, it is lost forever. We prove a slight generalization of that, namely that whenever agent a is an expert and
![]() $K_a\mathsf{magic}$
is false, it remains false. The condition that a is an expert is relevant, because before a is an expert
$K_a\mathsf{magic}$
is false, it remains false. The condition that a is an expert is relevant, because before a is an expert
![]() $K_a\mathsf{magic}$
is also false (but a magic call may then still happen). This covers all cases in which a could have become an expert, also those where magic never held sway.
$K_a\mathsf{magic}$
is also false (but a magic call may then still happen). This covers all cases in which a could have become an expert, also those where magic never held sway.
Lemma 17.
![]() $\neg K_a\mathsf{magic}$
is equivalent to
$\neg K_a\mathsf{magic}$
is equivalent to
![]() $\bigvee_{B\subseteq A} (K_a \mathit{Exp}_B \wedge \hat{K}_a \mathit{NExp}_{A{\setminus}B})$
.
$\bigvee_{B\subseteq A} (K_a \mathit{Exp}_B \wedge \hat{K}_a \mathit{NExp}_{A{\setminus}B})$
.
Note that B may be the empty set, in which case agent a is not an expert (where
![]() $\mathit{Exp}_\emptyset = \top$
).
$\mathit{Exp}_\emptyset = \top$
).
Proof. We have that
![]() $K_a\mathsf{magic}$
is by definition
$K_a\mathsf{magic}$
is by definition
![]() $K_a \bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a \mathit{Exp}_d)$
, such that its negation is equivalent to
$K_a \bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a \mathit{Exp}_d)$
, such that its negation is equivalent to
![]() $\hat{K}_a \bigwedge_{d \in A} (\mathit{Exp}_d \rightarrow K_a \mathit{Exp}_d)$
. Assume some call sequence
$\hat{K}_a \bigwedge_{d \in A} (\mathit{Exp}_d \rightarrow K_a \mathit{Exp}_d)$
. Assume some call sequence
![]() $\sigma$
satisfies the latter. Then there is a
$\sigma$
satisfies the latter. Then there is a
![]() $\tau \sim_a \sigma$
such that for all
$\tau \sim_a \sigma$
such that for all
![]() $d \in A$
,
$d \in A$
,
![]() $\tau\models \mathit{Exp}_d \rightarrow K_a \mathit{Exp}_d$
. Let now
$\tau\models \mathit{Exp}_d \rightarrow K_a \mathit{Exp}_d$
. Let now
![]() $B = \{d \in A \mid \tau \models \mathit{Exp}_d\}$
, then
$B = \{d \in A \mid \tau \models \mathit{Exp}_d\}$
, then
![]() $\tau\models K_a \mathit{Exp}_B$
and
$\tau\models K_a \mathit{Exp}_B$
and
![]() $\tau \models \mathit{NExp}_{A{\setminus}B}$
. Therefore,
$\tau \models \mathit{NExp}_{A{\setminus}B}$
. Therefore,
![]() $\sigma \models K_a \mathit{Exp}_B$
and
$\sigma \models K_a \mathit{Exp}_B$
and
![]() $\sigma \models \hat{K}_a \mathit{NExp}_{A{\setminus}B}$
so that
$\sigma \models \hat{K}_a \mathit{NExp}_{A{\setminus}B}$
so that
![]() $\sigma \models \bigvee_{B\subseteq A} (K_a \mathit{Exp}_B \wedge \hat{K}_a \mathit{NExp}_{A{\setminus}B})$
. The other direction is similar and left to the reader.
$\sigma \models \bigvee_{B\subseteq A} (K_a \mathit{Exp}_B \wedge \hat{K}_a \mathit{NExp}_{A{\setminus}B})$
. The other direction is similar and left to the reader.
So if magic is false, agent a considers a call sequence possible wherein all agents she is uncertain about are non-experts. In combination with Lemma 9, this implies that she considers a call sequence possible wherein all non-experts hold the same secrets as in the actual call sequence. As a consequence, a can never be surprised by later finding out in a call how many secrets a non-expert actually holds, a property that will be used frequently in later proofs.
Lemma 18. Consider a sequence
![]() $\sigma\kern-0.8pt{.}ab$
such that in the last call a and b become experts. Then
$\sigma\kern-0.8pt{.}ab$
such that in the last call a and b become experts. Then
![]() $\sigma\kern-0.8pt{.}ab\models\neg K_a \mathsf{magic}$
.
$\sigma\kern-0.8pt{.}ab\models\neg K_a \mathsf{magic}$
.
Proof. By Proposition 11, we get
![]() $\sigma\kern-0.8pt{.}ab \models \hat{K}_a \mathit{NExp}_{A{-}ab}$
. Together with
$\sigma\kern-0.8pt{.}ab \models \hat{K}_a \mathit{NExp}_{A{-}ab}$
. Together with
![]() $\sigma\kern-0.8pt{.}ab\models K_a \mathit{Exp}_{ab}$
, we can apply Lemma 17 choosing
$\sigma\kern-0.8pt{.}ab\models K_a \mathit{Exp}_{ab}$
, we can apply Lemma 17 choosing
![]() $B=\{a,b\}$
to get
$B=\{a,b\}$
to get
![]() $\sigma\kern-0.8pt{.}ab\models\neg K_a \mathsf{magic}$
.
$\sigma\kern-0.8pt{.}ab\models\neg K_a \mathsf{magic}$
.
Lemma 19. Let
![]() $\sigma\kern-0.8pt{.}ab$
be given wherein a became expert in the lucky call ab. Then
$\sigma\kern-0.8pt{.}ab$
be given wherein a became expert in the lucky call ab. Then
![]() $\sigma\kern-0.8pt{.}ab\models\neg K_a \mathsf{magic}$
.
$\sigma\kern-0.8pt{.}ab\models\neg K_a \mathsf{magic}$
.
Proof. Suppose that a was lucky about agent c. Then
![]() $\sigma\kern-0.8pt{.}ab \models K_a \mathit{Exp}_{abc} \wedge \hat{K}_a \mathit{NExp}_{A{-}abc}$
. Now by using Lemma 17 for
$\sigma\kern-0.8pt{.}ab \models K_a \mathit{Exp}_{abc} \wedge \hat{K}_a \mathit{NExp}_{A{-}abc}$
. Now by using Lemma 17 for
![]() $B = \{a,b,c\}$
, we get
$B = \{a,b,c\}$
, we get
![]() $\sigma\kern-0.8pt{.}ab\models\neg K_a \mathsf{magic}$
.
$\sigma\kern-0.8pt{.}ab\models\neg K_a \mathsf{magic}$
.
Lemma 20. Let
![]() $\sigma\models \mathit{Exp}_a$
and
$\sigma\models \mathit{Exp}_a$
and
![]() $\tau$
with
$\tau$
with
![]() $\sigma\sqsubseteq\tau$
be given. If
$\sigma\sqsubseteq\tau$
be given. If
![]() $\sigma\not\models K_a\mathsf{magic}$
then
$\sigma\not\models K_a\mathsf{magic}$
then
![]() $\tau\not\models K_a\mathsf{magic}$
.
$\tau\not\models K_a\mathsf{magic}$
.
Proof. Given
![]() $\sigma\models\mathit{Exp}_a$
and
$\sigma\models\mathit{Exp}_a$
and
![]() $\sigma\not\models K_a\mathsf{magic}$
, there is a non-empty
$\sigma\not\models K_a\mathsf{magic}$
, there is a non-empty
![]() $B \subseteq A$
such that a knows that all agents in B are experts and considers it possible that all agents not in B are non-experts. The proof is now by induction on the number m of calls involving a in
$B \subseteq A$
such that a knows that all agents in B are experts and considers it possible that all agents not in B are non-experts. The proof is now by induction on the number m of calls involving a in
![]() $\tau{\setminus}\sigma$
.
$\tau{\setminus}\sigma$
.
Base case
If
![]() $m=0$
, then
$m=0$
, then
![]() $\tau\sim_a\sigma$
. As
$\tau\sim_a\sigma$
. As
![]() $\hat{K}_a \bigwedge_{d \in A} (\mathit{Exp}_d\rightarrow K_a \mathit{Exp}_d)$
is equivalent to
$\hat{K}_a \bigwedge_{d \in A} (\mathit{Exp}_d\rightarrow K_a \mathit{Exp}_d)$
is equivalent to
![]() $K_a\hat{K}_a \bigwedge_{d \in A} (\mathit{Exp}_d\rightarrow K_a \mathit{Exp}_d)$
,
$K_a\hat{K}_a \bigwedge_{d \in A} (\mathit{Exp}_d\rightarrow K_a \mathit{Exp}_d)$
,
![]() $\sigma\models\neg{K_a\mathsf{magic}}$
is equivalent to
$\sigma\models\neg{K_a\mathsf{magic}}$
is equivalent to
![]() $\sigma\models K_a\neg{K_a\mathsf{magic}}$
, from which it follows that
$\sigma\models K_a\neg{K_a\mathsf{magic}}$
, from which it follows that
![]() $\tau\models\neg{K_a\mathsf{magic}}$
, that is,
$\tau\models\neg{K_a\mathsf{magic}}$
, that is,
![]() $\tau\not\models{K_a\mathsf{magic}}$
.
$\tau\not\models{K_a\mathsf{magic}}$
.
Induction step
Now assume
![]() $\tau{\setminus}\sigma$
contains
$\tau{\setminus}\sigma$
contains
![]() $m>0$
calls involving a. By induction, we assume that all but the last preserve
$m>0$
calls involving a. By induction, we assume that all but the last preserve
![]() $\neg K_a\mathsf{magic}_a$
. Let ab be the last call by a. We need to distinguish three cases.
$\neg K_a\mathsf{magic}_a$
. Let ab be the last call by a. We need to distinguish three cases.
Case b is a known expert: A call to a known expert is not informative. Let
![]() $\tau = \sigma\kern-0.8pt{.}\tau_1.ab.\tau_2$
, then we assume
$\tau = \sigma\kern-0.8pt{.}\tau_1.ab.\tau_2$
, then we assume
![]() $\sigma\kern-0.8pt{.}\tau_1\models K_a \mathit{Exp}_b$
. We may assume by induction that there is a
$\sigma\kern-0.8pt{.}\tau_1\models K_a \mathit{Exp}_b$
. We may assume by induction that there is a
![]() $\tau_3$
such that
$\tau_3$
such that
![]() $\sigma\kern-0.8pt{.}\tau_1 \sim_a \tau_3$
and
$\sigma\kern-0.8pt{.}\tau_1 \sim_a \tau_3$
and
![]() $\tau_3\models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
, where
$\tau_3\models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
, where
![]() $a,b \in B \subseteq A$
. As
$a,b \in B \subseteq A$
. As
![]() $\tau_3\models \mathit{Exp}_B$
, also
$\tau_3\models \mathit{Exp}_B$
, also
![]() $\tau_3.ab\models \mathit{Exp}_B$
. Furthermore, as
$\tau_3.ab\models \mathit{Exp}_B$
. Furthermore, as
![]() $\tau_3\models \mathit{NExp}_{A{\setminus}B}$
and
$\tau_3\models \mathit{NExp}_{A{\setminus}B}$
and
![]() $a,b\notin {A{\setminus}B}$
, from the semantics of calls we obtain
$a,b\notin {A{\setminus}B}$
, from the semantics of calls we obtain
![]() $\tau_3.ab \models \mathit{NExp}_{A{\setminus}B}$
. Therefore,
$\tau_3.ab \models \mathit{NExp}_{A{\setminus}B}$
. Therefore,
![]() $\tau_3.ab\models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. From that and
$\tau_3.ab\models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. From that and
![]() $\sigma\kern-0.8pt{.}\tau_1.ab \sim_a \tau_3.ab$
, it then follows that
$\sigma\kern-0.8pt{.}\tau_1.ab \sim_a \tau_3.ab$
, it then follows that
![]() $\sigma\kern-0.8pt{.}\tau_1.ab \models \neg{K_a\mathsf{magic}}$
.
$\sigma\kern-0.8pt{.}\tau_1.ab \models \neg{K_a\mathsf{magic}}$
.
Case b is an unknown expert: Agent a now considers it possible that b became an expert by calling an agent c that a already knew to be expert. Therefore, if before call ab agent a knew that all agents in B are experts and considered it possible that all agents in
![]() $A{\setminus}B$
are non-experts, after the call ab agent a knows all agents in
$A{\setminus}B$
are non-experts, after the call ab agent a knows all agents in
![]() $B{+}b$
are experts and considers it possible that the remaining agents, in
$B{+}b$
are experts and considers it possible that the remaining agents, in
![]() $(A{\setminus}B){-}b$
, are non-experts, and
$(A{\setminus}B){-}b$
, are non-experts, and
![]() $K_a \mathsf{magic}_a$
is still false.
$K_a \mathsf{magic}_a$
is still false.
Formally, we proceed as in the previous case and assume by induction that there is a
![]() $\tau_3$
such that
$\tau_3$
such that
![]() $\sigma\kern-0.8pt{.}\tau_1 \sim_a \tau_3$
and
$\sigma\kern-0.8pt{.}\tau_1 \sim_a \tau_3$
and
![]() $\tau_3\models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
, where in this case
$\tau_3\models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
, where in this case
![]() $c \in B$
and
$c \in B$
and
![]() $b \in A{\setminus}B$
. Except that we now use this to argue that
$b \in A{\setminus}B$
. Except that we now use this to argue that
![]() $\sigma\kern-0.8pt{.}\tau_1.ab \sim_a \tau_3.\pmb{bc}.ab$
, which brings us from
$\sigma\kern-0.8pt{.}\tau_1.ab \sim_a \tau_3.\pmb{bc}.ab$
, which brings us from
![]() $\tau_3\models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
to
$\tau_3\models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
to
![]() $\tau_3.bc\models \mathit{Exp}_{B{+}b} \wedge \mathit{NExp}_{A{\setminus}(B{+}b)}$
. Further details are left to the reader.
$\tau_3.bc\models \mathit{Exp}_{B{+}b} \wedge \mathit{NExp}_{A{\setminus}(B{+}b)}$
. Further details are left to the reader.
Case b is a non-expert: By inductive assumption, there is a
![]() $\tau_3$
with
$\tau_3$
with
![]() $\sigma\kern-0.8pt{.}\tau_1 \sim_a \tau_3$
and
$\sigma\kern-0.8pt{.}\tau_1 \sim_a \tau_3$
and
![]() $\tau_3\models \mathit{NExp}_{A{\setminus}B}$
. From Lemma 9, we may assume some such
$\tau_3\models \mathit{NExp}_{A{\setminus}B}$
. From Lemma 9, we may assume some such
![]() $\tau_3$
for which, for all
$\tau_3$
for which, for all
![]() $c \in A{\setminus}B$
,
$c \in A{\setminus}B$
,
![]() $c(\tau_3)= c((\sigma\kern-0.8pt{.}\tau_1)^{<c})$
. In particular, for
$c(\tau_3)= c((\sigma\kern-0.8pt{.}\tau_1)^{<c})$
. In particular, for
![]() $b=c$
,
$b=c$
,
![]() $b(\tau_3)=b((\sigma\kern-0.8pt{.}\tau_1)^{<b})=b(\sigma\kern-0.8pt{.}\tau_1)$
. From
$b(\tau_3)=b((\sigma\kern-0.8pt{.}\tau_1)^{<b})=b(\sigma\kern-0.8pt{.}\tau_1)$
. From
![]() $b(\tau_3)=b(\sigma\kern-0.8pt{.}\tau_1)$
and
$b(\tau_3)=b(\sigma\kern-0.8pt{.}\tau_1)$
and
![]() $\tau_3\sim_a\sigma\kern-0.8pt{.}\tau_1$
, we obtain that
$\tau_3\sim_a\sigma\kern-0.8pt{.}\tau_1$
, we obtain that
![]() $\tau_3.ab\sim_a\sigma\kern-0.8pt{.}\tau_1.ab$
. For all
$\tau_3.ab\sim_a\sigma\kern-0.8pt{.}\tau_1.ab$
. For all
![]() $c \in A{\setminus}B$
with
$c \in A{\setminus}B$
with
![]() $c \neq b$
, we have that
$c \neq b$
, we have that
![]() $c(\tau_3.ab)= c((\sigma\kern-0.8pt{.}\tau_1)^{<c}.ab)$
, as c is not involved in call ab. We now have that
$c(\tau_3.ab)= c((\sigma\kern-0.8pt{.}\tau_1)^{<c}.ab)$
, as c is not involved in call ab. We now have that
![]() $\tau\models K_a\mathit{Exp}_{B+b}\wedge\hat{K}_a\mathit{NExp}_{A{\setminus}(B+b)}$
so that
$\tau\models K_a\mathit{Exp}_{B+b}\wedge\hat{K}_a\mathit{NExp}_{A{\setminus}(B+b)}$
so that
![]() $\tau\models\neg K_a \mathsf{magic}$
.
$\tau\models\neg K_a \mathsf{magic}$
.
From Lemmas 18, 19, and 20, we immediately obtain:
Corollary 21. Any extension of a call sequence wherein an agent a became expert by calling another non-expert or became expert in a lucky call satisfies
![]() $\neg K_a\mathsf{magic}$
.
$\neg K_a\mathsf{magic}$
.
Finally, we now proceed with the characterization of lucky calls. In this subsection, we considered the case where expert a makes a call and magic does not hold (see Table 4).
Proposition 22. Expert to non-expert without magic. Let
![]() $\sigma \models \mathit{Exp}_a$
,
$\sigma \models \mathit{Exp}_a$
,
![]() $\sigma\not\models K_a \mathit{Exp}_b$
,
$\sigma\not\models K_a \mathit{Exp}_b$
,
![]() $\sigma \not\models \mathit{Exp}_c$
, and suppose that
$\sigma \not\models \mathit{Exp}_c$
, and suppose that
![]() $\sigma\not\models{K_a\mathsf{magic}}$
. Then
$\sigma\not\models{K_a\mathsf{magic}}$
. Then
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
.
Proof. From
![]() $\sigma\not\models K_a\mathsf{magic}$
, it follows by Lemma 17 that there is a
$\sigma\not\models K_a\mathsf{magic}$
, it follows by Lemma 17 that there is a
![]() $B \subseteq A$
such that
$B \subseteq A$
such that
![]() $\sigma \models K_a\mathit{Exp}_B\wedge \hat{K}_a\mathit{NExp}_{A{\setminus}B}$
. From assumption
$\sigma \models K_a\mathit{Exp}_B\wedge \hat{K}_a\mathit{NExp}_{A{\setminus}B}$
. From assumption
![]() $\sigma\not\models K_a \mathit{Exp}_c$
and together with assumption
$\sigma\not\models K_a \mathit{Exp}_c$
and together with assumption
![]() $\sigma\not\models K_a \mathit{Exp}_b$
, we deduce that
$\sigma\not\models K_a \mathit{Exp}_b$
, we deduce that
![]() $b,c \notin B$
, that is,
$b,c \notin B$
, that is,
![]() $b,c \in A{\setminus}B$
. From Lemma 9, we obtain a
$b,c \in A{\setminus}B$
. From Lemma 9, we obtain a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
,
$\sigma\sim_a\tau$
,
![]() $b(\sigma^{<b})=b(\tau)$
, and
$b(\sigma^{<b})=b(\tau)$
, and
![]() $c(\sigma^{<c})=c(\tau)$
. As
$c(\sigma^{<c})=c(\tau)$
. As
![]() $\sigma\not\models\mathit{Exp}_c$
,
$\sigma\not\models\mathit{Exp}_c$
,
![]() $c(\sigma^{<c})=c(\sigma)$
. From
$c(\sigma^{<c})=c(\sigma)$
. From
![]() $\sigma\sim_a \tau$
and
$\sigma\sim_a \tau$
and
![]() $c(\sigma)= c(\tau)$
, we obtain
$c(\sigma)= c(\tau)$
, we obtain
![]() $\sigma\kern-0.8pt{.}ac \sim\tau.ac$
. As
$\sigma\kern-0.8pt{.}ac \sim\tau.ac$
. As
![]() $\tau\models\neg\mathit{Exp}_b$
and
$\tau\models\neg\mathit{Exp}_b$
and
![]() $b\neq a,c$
, also
$b\neq a,c$
, also
![]() $\tau.ac\models\neg\mathit{Exp}_b$
. From
$\tau.ac\models\neg\mathit{Exp}_b$
. From
![]() $\sigma\kern-0.8pt{.}ac \sim_a\tau.ac$
and
$\sigma\kern-0.8pt{.}ac \sim_a\tau.ac$
and
![]() $\tau.ac\models\neg\mathit{Exp}_b$
, it follows that
$\tau.ac\models\neg\mathit{Exp}_b$
, it follows that
![]() $\sigma\kern-0.8pt{.}ac\not\models K_a\mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac\not\models K_a\mathit{Exp}_b$
.
5.7 Expert to non-expert – with magic
We recall formula
![]() $K_a\mathsf{magic}$
is defined as
$K_a\mathsf{magic}$
is defined as
![]() $K_a \bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a\mathit{Exp}_d)$
. This formula becomes true after any call sequence
$K_a \bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a\mathit{Exp}_d)$
. This formula becomes true after any call sequence
![]() $\sigma\kern-0.8pt{.}ab$
, wherein a non-expert a becomes an expert by calling an expert b.
$\sigma\kern-0.8pt{.}ab$
, wherein a non-expert a becomes an expert by calling an expert b.
If everyone is close except d (with respect to a, see Definition 16), then call ab was lucky. Otherwise, a later call involving a is lucky if a knows that all but two distant agents are experts, magic holds, and a then calls a distant agent who is a non-expert. This is independent from the number of close agents that a is uncertain about at that stage. So, a may be lucky from the moment she became expert until the moment she became super expert and at any time in between as well (after which she may still have to call the close agents that she does not know to be expert). The remainder of the section consists of proving all this.
Lemma 23.
![]() $K_a\mathsf{magic}$
is equivalent to
$K_a\mathsf{magic}$
is equivalent to
![]() $K_a \bigvee_{B \subseteq A}(\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
.
$K_a \bigvee_{B \subseteq A}(\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
.
Proof. Let
![]() $\sigma$
be arbitrary.
$\sigma$
be arbitrary.
(
![]() $\Rightarrow$
) Assume
$\Rightarrow$
) Assume
![]() $\sigma\models K_a\bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a\mathit{Exp}_d)$
and
$\sigma\models K_a\bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a\mathit{Exp}_d)$
and
![]() $\tau$
such that
$\tau$
such that
![]() $\tau\sim_a\sigma$
. Then there is a
$\tau\sim_a\sigma$
. Then there is a
![]() $d \in A$
such that
$d \in A$
such that
![]() $\tau\models\mathit{Exp}_d \wedge\neg K_a\mathit{Exp}_d$
. From
$\tau\models\mathit{Exp}_d \wedge\neg K_a\mathit{Exp}_d$
. From
![]() $\tau\models\neg K_a\mathit{Exp}_d$
, we further obtain that there is a
$\tau\models\neg K_a\mathit{Exp}_d$
, we further obtain that there is a
![]() $\rho\sim_a\tau$
with
$\rho\sim_a\tau$
with
![]() $\rho\not\models\mathit{Exp}_d$
. Let
$\rho\not\models\mathit{Exp}_d$
. Let
![]() $B = \{c \in A\mid \tau\models\mathit{Exp}_c \}$
. Then
$B = \{c \in A\mid \tau\models\mathit{Exp}_c \}$
. Then
![]() $\tau\models\mathit{Exp}_B\wedge\mathit{NExp}_{A{\setminus}B}$
. As
$\tau\models\mathit{Exp}_B\wedge\mathit{NExp}_{A{\setminus}B}$
. As
![]() $d \in B$
and
$d \in B$
and
![]() $\rho\not\models\mathit{Exp}_d$
, we also have
$\rho\not\models\mathit{Exp}_d$
, we also have
![]() $\rho\not\models\mathit{Exp}_B$
, and from that and
$\rho\not\models\mathit{Exp}_B$
, and from that and
![]() $\rho\sim_a\tau$
, we obtain
$\rho\sim_a\tau$
, we obtain
![]() $\tau\models\neg K_a \mathit{Exp}_B$
. Altogether we obtained
$\tau\models\neg K_a \mathit{Exp}_B$
. Altogether we obtained
![]() $\tau\models\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. As
$\tau\models\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. As
![]() $\tau\sim_a\sigma$
was arbitrary, it follows that
$\tau\sim_a\sigma$
was arbitrary, it follows that
![]() $\sigma\models K_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \hat{K}_a \mathit{NExp}_{A{\setminus}B})$
.
$\sigma\models K_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \hat{K}_a \mathit{NExp}_{A{\setminus}B})$
.
(
![]() $\Leftarrow$
) Now assume
$\Leftarrow$
) Now assume
![]() $\sigma\models K_a \bigvee_{B \subseteq A}(\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
, and
$\sigma\models K_a \bigvee_{B \subseteq A}(\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
, and
![]() $\tau$
such that
$\tau$
such that
![]() $\tau\sim_a\sigma$
. Then there is a B such that
$\tau\sim_a\sigma$
. Then there is a B such that
![]() $\tau\models \mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. From
$\tau\models \mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. From
![]() $\tau\models \mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B$
, it follows that there is a
$\tau\models \mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B$
, it follows that there is a
![]() $d \in B$
with
$d \in B$
with
![]() $\tau\models\mathit{Exp}_d\wedge\neg K_a\mathit{Exp}_d$
, and from that we almost directly obtain
$\tau\models\mathit{Exp}_d\wedge\neg K_a\mathit{Exp}_d$
, and from that we almost directly obtain
![]() $\sigma\models K_a\bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a\mathit{Exp}_d)$
.
$\sigma\models K_a\bigvee_{d \in A} (\mathit{Exp}_d \wedge \neg K_a\mathit{Exp}_d)$
.
Lemma 23 by itself should not impress. Once I have made even a single call, I even consider it possible that everyone is an expert (
![]() $A=B$
) without knowing it. The interest is in the minimal B for which it holds. For this, we first need to investigate the magic call.
$A=B$
) without knowing it. The interest is in the minimal B for which it holds. For this, we first need to investigate the magic call.
Lemma 24. Let a become expert in magic call ab. Then for all distant
![]() $c\neq a,b$
, a considers it possible that b and c became expert in the previous call.
$c\neq a,b$
, a considers it possible that b and c became expert in the previous call.
Formally, let
![]() $\sigma\models\neg\mathit{Exp}_a\wedge\mathit{Exp}_b$
and
$\sigma\models\neg\mathit{Exp}_a\wedge\mathit{Exp}_b$
and
![]() $\sigma\not\models\bigvee_{d\in A} K_a \mathit{Exp}_{bc}(A-d)$
. Then there is a
$\sigma\not\models\bigvee_{d\in A} K_a \mathit{Exp}_{bc}(A-d)$
. Then there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\tau.bc.ab \sim_a \sigma\kern-0.8pt{.}ab$
and
$\tau.bc.ab \sim_a \sigma\kern-0.8pt{.}ab$
and
![]() $\tau\models\neg\mathit{Exp}_b\wedge\neg\mathit{Exp}_c$
.
$\tau\models\neg\mathit{Exp}_b\wedge\neg\mathit{Exp}_c$
.
Proof. The proof is by case distinction on what a knows about b and c. In the proof we use that, as b was an expert in magic call ab, agent a must have known at least one other secret than her own, because otherwise b could not have become an expert. So call sequence
![]() $\sigma$
preceding ab must contain at least one call involving a. We can then let the other agent involved in that call take the place of agent a in the hypothetical reasoning below (concerning extensions not involving a of call sequences). We cannot use a herself, as agent a is aware of all calls involving her, so she does not consider it possible that she made more calls than she actually did.
$\sigma$
preceding ab must contain at least one call involving a. We can then let the other agent involved in that call take the place of agent a in the hypothetical reasoning below (concerning extensions not involving a of call sequences). We cannot use a herself, as agent a is aware of all calls involving her, so she does not consider it possible that she made more calls than she actually did.
Case
![]() $b \notin a(\sigma)$
and
$b \notin a(\sigma)$
and
![]() $c \notin a(\sigma)$
: Note that
$c \notin a(\sigma)$
: Note that
![]() $|a(\sigma)|\geq 2$
as ab was magic (see above). Following
$|a(\sigma)|\geq 2$
as ab was magic (see above). Following
![]() $\sigma^a_\ll$
, let all agents in
$\sigma^a_\ll$
, let all agents in
![]() $a(\sigma)$
except a call all agents in
$a(\sigma)$
except a call all agents in
![]() $A{-}abc$
until they are all
$A{-}abc$
until they are all
![]() $A{-}abc$
experts. As this must involve an agent who already called a, the secret of a is also passed along. This is call sequence
$A{-}abc$
experts. As this must involve an agent who already called a, the secret of a is also passed along. This is call sequence
![]() $\sigma_1$
. Pick any
$\sigma_1$
. Pick any
![]() $d \in A{-}abc$
. Let then c call d and after that b call c. In the final call bc, non-experts b,c become experts. We now have that
$d \in A{-}abc$
. Let then c call d and after that b call c. In the final call bc, non-experts b,c become experts. We now have that
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma^a_\ll.\sigma_1.cd.bc.ab$
. (Note that
$\sigma\kern-0.8pt{.}ab \sim_a \sigma^a_\ll.\sigma_1.cd.bc.ab$
. (Note that
![]() $\sigma^a_\ll.\sigma_1.cd.bc.ab \models \mathit{Exp}_{abc} \wedge \mathit{NExp}_{A{-}abc}$
.)
$\sigma^a_\ll.\sigma_1.cd.bc.ab \models \mathit{Exp}_{abc} \wedge \mathit{NExp}_{A{-}abc}$
.)
Case
![]() $b \notin a(\sigma)$
and
$b \notin a(\sigma)$
and
![]() $c \in a(\sigma)$
: Following
$c \in a(\sigma)$
: Following
![]() $\sigma^a_\ll$
, we now let all in
$\sigma^a_\ll$
, we now let all in
![]() $A{-}ab$
call each other, let this be
$A{-}ab$
call each other, let this be
![]() $\sigma_2$
, and let then b call c. In this case,
$\sigma_2$
, and let then b call c. In this case,
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma^a_\ll.\sigma_2.bc.ab$
.
$\sigma\kern-0.8pt{.}ab \sim_a \sigma^a_\ll.\sigma_2.bc.ab$
.
Case
![]() $b \in a(\sigma)$
and
$b \in a(\sigma)$
and
![]() $c \notin a(\sigma)$
: Following
$c \notin a(\sigma)$
: Following
![]() $\sigma^a_\ll$
we now let all in
$\sigma^a_\ll$
we now let all in
![]() $A{-}ac$
call each other, let this be
$A{-}ac$
call each other, let this be
![]() $\sigma_3$
, and let then b call c. In this case, again,
$\sigma_3$
, and let then b call c. In this case, again,
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma^a_\ll.\sigma_1.bc.ab$
.
$\sigma\kern-0.8pt{.}ab \sim_a \sigma^a_\ll.\sigma_1.bc.ab$
.
Case
![]() $b \in a(\sigma)$
and
$b \in a(\sigma)$
and
![]() $c \in a(\sigma)$
: Because of the assumption
$c \in a(\sigma)$
: Because of the assumption
![]() $\sigma\not\models\bigvee_{d\in A} K_a \mathit{Exp}_{bc}(A-d)$
, it is not the case that
$\sigma\not\models\bigvee_{d\in A} K_a \mathit{Exp}_{bc}(A-d)$
, it is not the case that
![]() $a(\sigma)=b(\sigma)=c(\sigma)=A{-}d$
. It must therefore be the case that
$a(\sigma)=b(\sigma)=c(\sigma)=A{-}d$
. It must therefore be the case that
![]() $c(\sigma) \subsetneq A{-}d$
or that
$c(\sigma) \subsetneq A{-}d$
or that
![]() $b(\sigma) \subsetneq A{-}d$
so that b or c know fewer secrets than present in
$b(\sigma) \subsetneq A{-}d$
so that b or c know fewer secrets than present in
![]() $a(\sigma)$
.
$a(\sigma)$
.
First assume
![]() $c(\sigma) \subsetneq A{-}d$
. Now if
$c(\sigma) \subsetneq A{-}d$
. Now if
![]() $c(\sigma)=A{-}bd$
, we execute
$c(\sigma)=A{-}bd$
, we execute
![]() $(\sigma^a_\ll \cup_\sigma \sigma^c_\ll).cd.bc$
in which case in call bc agents b and c become experts and we also have
$(\sigma^a_\ll \cup_\sigma \sigma^c_\ll).cd.bc$
in which case in call bc agents b and c become experts and we also have
![]() $\sigma\kern-0.8pt{.}ab \sim_a (\sigma^a_\ll \cup_\sigma \sigma^c_\ll).cd.bc.ab$
. Otherwise, let
$\sigma\kern-0.8pt{.}ab \sim_a (\sigma^a_\ll \cup_\sigma \sigma^c_\ll).cd.bc.ab$
. Otherwise, let
![]() $e \neq a,b,c,d$
be such that
$e \neq a,b,c,d$
be such that
![]() $e \notin c(\sigma)$
and
$e \notin c(\sigma)$
and
![]() $e \in a(\sigma)$
. Note that there must then be at least five agents. Following
$e \in a(\sigma)$
. Note that there must then be at least five agents. Following
![]() $\sigma^a_\ll$
, we now first let c call d (e remains unknown to either), let then all agents in
$\sigma^a_\ll$
, we now first let c call d (e remains unknown to either), let then all agents in
![]() $A{-}acd$
call each other, let this be
$A{-}acd$
call each other, let this be
![]() $\sigma_4$
, and finally let c call b. If c was the only agent, apart from a herself, knowing the secret of a, then in that call bc agent c informs b of new secrets a and d. Otherwise, b already knew a and was only informed of d. We now have that
$\sigma_4$
, and finally let c call b. If c was the only agent, apart from a herself, knowing the secret of a, then in that call bc agent c informs b of new secrets a and d. Otherwise, b already knew a and was only informed of d. We now have that
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma^a_\ll.cd.\sigma_4.bc.ab$
.
$\sigma\kern-0.8pt{.}ab \sim_a \sigma^a_\ll.cd.\sigma_4.bc.ab$
.
Next assume
![]() $b(\sigma) \subsetneq A{-}d$
. This case is similar to the previous case.
$b(\sigma) \subsetneq A{-}d$
. This case is similar to the previous case.
Corollary 25. Let agent a become expert in magic call ab. Then for all close agents
![]() $c \neq a,b$
, agent a knows that b and c did not both become expert in the previous call.
$c \neq a,b$
, agent a knows that b and c did not both become expert in the previous call.
However, it may well be that b became expert in a previous call with a close c in which c was already an expert. That is because the only way a close c can make close b an expert is by making b learn the secret of the d that both do not know. But for that to happen, c must know d and therefore is already an expert.
Corollary 26. Let a become expert in magic call ab. Then for all distant
![]() $c\neq a,b$
, a considers it possible that c is the only unknown expert.
$c\neq a,b$
, a considers it possible that c is the only unknown expert.
Given
![]() $\sigma$
and a, let us call a set B distant-minimal if
$\sigma$
and a, let us call a set B distant-minimal if
![]() $\sigma\models\hat{K}_a (\mathit{Exp}_B \wedge \neg K_a \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
but for all distant c,
$\sigma\models\hat{K}_a (\mathit{Exp}_B \wedge \neg K_a \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
but for all distant c,
![]() $\sigma\not\models\hat{K}_a (\mathit{Exp}_{B{-}c} \wedge \neg K_a \mathit{Exp}_{B{-}c} \wedge \mathit{NExp}_{A{\setminus}(B{-}c)})$
. If B is distant-minimal, there is a single distant
$\sigma\not\models\hat{K}_a (\mathit{Exp}_{B{-}c} \wedge \neg K_a \mathit{Exp}_{B{-}c} \wedge \mathit{NExp}_{A{\setminus}(B{-}c)})$
. If B is distant-minimal, there is a single distant
![]() $d \in B$
that is an unknown expert for a.
$d \in B$
that is an unknown expert for a.
Lemma 27. Let
![]() $\sigma$
be given with
$\sigma$
be given with
![]() $\sigma\models K_a \mathsf{magic}$
. Then for all distant-minimal
$\sigma\models K_a \mathsf{magic}$
. Then for all distant-minimal
![]() $B\subseteq A$
, there is a
$B\subseteq A$
, there is a
![]() $\tau\sim_a\sigma$
such that for all
$\tau\sim_a\sigma$
such that for all
![]() $c \in A{\setminus}B$
,
$c \in A{\setminus}B$
,
![]() $c(\sigma^{<c}) = c(\tau)$
.
$c(\sigma^{<c}) = c(\tau)$
.
Proof. We prove this by induction on the number of calls involving a in
![]() $\sigma$
after which a is an expert.
$\sigma$
after which a is an expert.
Basis Magic is established in a magic call ab. We may assume that
![]() $\sigma = \sigma\kern-0.8pt{.}ab$
where
$\sigma = \sigma\kern-0.8pt{.}ab$
where
![]() $\sigma\models\neg\mathit{Exp}_a\wedge\mathit{Exp}_b$
(strictly, we should assume
$\sigma\models\neg\mathit{Exp}_a\wedge\mathit{Exp}_b$
(strictly, we should assume
![]() $\sigma = \sigma\kern-0.8pt{.}ab.\xi$
where
$\sigma = \sigma\kern-0.8pt{.}ab.\xi$
where
![]() $\xi$
contains no call involving a; however, as we prove something about the knowledge of a, and
$\xi$
contains no call involving a; however, as we prove something about the knowledge of a, and
![]() $\sigma\kern-0.8pt{.}ab \sim_a \tau$
if
$\sigma\kern-0.8pt{.}ab \sim_a \tau$
if
![]() $\sigma\kern-0.8pt{.}ab.\xi \sim_a \tau$
for all
$\sigma\kern-0.8pt{.}ab.\xi \sim_a \tau$
for all
![]() $\xi$
, we assume
$\xi$
, we assume
![]() $\xi=\epsilon$
).
$\xi=\epsilon$
).
As call ab was magic,
![]() $\sigma\kern-0.8pt{.}ab \models K_a \bigvee_{B \subseteq A}(\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
(Lemma 23). We now choose
$\sigma\kern-0.8pt{.}ab \models K_a \bigvee_{B \subseteq A}(\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
(Lemma 23). We now choose
![]() $\rho$
and distant-minimal B such that
$\rho$
and distant-minimal B such that
![]() $\rho.ab \sim_a \sigma\kern-0.8pt{.}ab$
and
$\rho.ab \sim_a \sigma\kern-0.8pt{.}ab$
and
![]() $\rho.ab \models \mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. From Lemma 9, it follows that there is a
$\rho.ab \models \mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. From Lemma 9, it follows that there is a
![]() $\tau.ab\sim_a\sigma\kern-0.8pt{.}ab$
with for all
$\tau.ab\sim_a\sigma\kern-0.8pt{.}ab$
with for all
![]() $c \in A{\setminus}B$
,
$c \in A{\setminus}B$
,
![]() $c(\tau.ab) = c({(\sigma\kern-0.8pt{.}ab)}^{<c})$
. This does not seem to rule out that there may be more non-experts in
$c(\tau.ab) = c({(\sigma\kern-0.8pt{.}ab)}^{<c})$
. This does not seem to rule out that there may be more non-experts in
![]() $\tau$
than those in
$\tau$
than those in
![]() $A{\setminus}B$
. However, we can rule this out given our previous results. From
$A{\setminus}B$
. However, we can rule this out given our previous results. From
![]() $\tau.ab \sim_a \sigma\kern-0.8pt{.}ab$
and again applying Lemma 23, it follows that there must be a C such that
$\tau.ab \sim_a \sigma\kern-0.8pt{.}ab$
and again applying Lemma 23, it follows that there must be a C such that
![]() $\tau.ab \models \mathit{Exp}_C \wedge \neg K_a\mathit{Exp}_C \wedge \mathit{NExp}_{A{\setminus}C}$
. As B was distant-minimal, we cannot have that
$\tau.ab \models \mathit{Exp}_C \wedge \neg K_a\mathit{Exp}_C \wedge \mathit{NExp}_{A{\setminus}C}$
. As B was distant-minimal, we cannot have that
![]() $C \subsetneq B$
and therefore
$C \subsetneq B$
and therefore
![]() $C=B$
. (Every expert in
$C=B$
. (Every expert in
![]() $\tau$
is also an expert in
$\tau$
is also an expert in
![]() $\rho$
.) This fulfills the proof requirements.
$\rho$
.) This fulfills the proof requirements.
Induction Let us now assume
![]() $\sigma = \sigma\kern-0.8pt{.}ab$
and
$\sigma = \sigma\kern-0.8pt{.}ab$
and
![]() $\sigma\kern-0.8pt{.}ab\models K_a \mathsf{magic}$
. If
$\sigma\kern-0.8pt{.}ab\models K_a \mathsf{magic}$
. If
![]() $\sigma\not\models K_a\mathsf{magic}$
, then
$\sigma\not\models K_a\mathsf{magic}$
, then
![]() $\sigma\kern-0.8pt{.}ab\not\models K_a \mathsf{magic}$
(Lemma 20). Therefore, we may assume that
$\sigma\kern-0.8pt{.}ab\not\models K_a \mathsf{magic}$
(Lemma 20). Therefore, we may assume that
![]() $\sigma \models K_a \mathsf{magic}$
. Let B be distant-minimal such that
$\sigma \models K_a \mathsf{magic}$
. Let B be distant-minimal such that
![]() $\sigma\kern-0.8pt{.}ab \models \hat{K}_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
.
$\sigma\kern-0.8pt{.}ab \models \hat{K}_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
.
We now show that if b is a non-expert, a known expert, or an unknown close expert, the proof requirements are met for
![]() $\sigma\kern-0.8pt{.}ab$
, whereas if b is an unknown distant expert,
$\sigma\kern-0.8pt{.}ab$
, whereas if b is an unknown distant expert,
![]() $\sigma\kern-0.8pt{.}ab\not\models K_a\mathsf{magic}$
.
$\sigma\kern-0.8pt{.}ab\not\models K_a\mathsf{magic}$
.
Case non-expert As b is now expert,
![]() $b \in B$
, and therefore, as b was a non-expert,
$b \in B$
, and therefore, as b was a non-expert,
![]() $\sigma\kern-0.8pt{.}ab \models \hat{K}_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
iff
$\sigma\kern-0.8pt{.}ab \models \hat{K}_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
iff
![]() $\sigma \models \hat{K}_a (\mathit{Exp}_{B{-}b} \wedge \neg K_a\mathit{Exp}_{B{-}b} \wedge \mathit{NExp}_{A{\setminus}(B{-}b)})$
. Suppose toward a contradiction that
$\sigma \models \hat{K}_a (\mathit{Exp}_{B{-}b} \wedge \neg K_a\mathit{Exp}_{B{-}b} \wedge \mathit{NExp}_{A{\setminus}(B{-}b)})$
. Suppose toward a contradiction that
![]() $B{-}b$
is not distant-minimal. Then there is a
$B{-}b$
is not distant-minimal. Then there is a
![]() $d \in B{-}b$
and a call sequence
$d \in B{-}b$
and a call sequence
![]() $\rho'$
such that
$\rho'$
such that
![]() $\sigma\sim_a \rho'$
and
$\sigma\sim_a \rho'$
and
![]() $\sigma\models \mathit{Exp}_{B{-}bd} \wedge \neg K_a\mathit{Exp}_{B{-}bd} \wedge \mathit{NExp}_{A{\setminus}(B{-}bd)}$
. We would then have that
$\sigma\models \mathit{Exp}_{B{-}bd} \wedge \neg K_a\mathit{Exp}_{B{-}bd} \wedge \mathit{NExp}_{A{\setminus}(B{-}bd)}$
. We would then have that
![]() $\sigma\kern-0.8pt{.}ab\sim_a \rho'.ab$
and
$\sigma\kern-0.8pt{.}ab\sim_a \rho'.ab$
and
![]() $\rho'.ab\models \mathit{Exp}_{B{-}d} \wedge \neg K_a\mathit{Exp}_{B{-}d} \wedge \mathit{NExp}_{A{\setminus}(B{-}d)}$
, contradicting the distant-minimality of B.
$\rho'.ab\models \mathit{Exp}_{B{-}d} \wedge \neg K_a\mathit{Exp}_{B{-}d} \wedge \mathit{NExp}_{A{\setminus}(B{-}d)}$
, contradicting the distant-minimality of B.
As
![]() $B{-}b$
is distant-minimal, by inductive hypothesis there is a
$B{-}b$
is distant-minimal, by inductive hypothesis there is a
![]() $\tau$
such that
$\tau$
such that
![]() $\tau\sim_a\sigma$
and for all
$\tau\sim_a\sigma$
and for all
![]() $c \in A{\setminus}(B{-}b)$
,
$c \in A{\setminus}(B{-}b)$
,
![]() $c(\sigma^{<c}) = c(\tau)$
. In particular, it follows that
$c(\sigma^{<c}) = c(\tau)$
. In particular, it follows that
![]() $b(\sigma^{<b})=b(\sigma) = b(\tau)$
. From that and
$b(\sigma^{<b})=b(\sigma) = b(\tau)$
. From that and
![]() $\tau\sim_a\sigma$
, we obtain that
$\tau\sim_a\sigma$
, we obtain that
![]() $\tau.ab \sim_a \sigma\kern-0.8pt{.}ab$
. It remains the case that for all
$\tau.ab \sim_a \sigma\kern-0.8pt{.}ab$
. It remains the case that for all
![]() $c \in A{\setminus}B$
,
$c \in A{\setminus}B$
,
![]() $c(\sigma^{<c}) = c(\tau)$
. As c is not involved in call ab, for all
$c(\sigma^{<c}) = c(\tau)$
. As c is not involved in call ab, for all
![]() $c \in A{\setminus}B$
we also have
$c \in A{\setminus}B$
we also have
![]() $c({(\sigma\kern-0.8pt{.}ab)}^{<c}) = c(\tau.ab)$
, as required.
$c({(\sigma\kern-0.8pt{.}ab)}^{<c}) = c(\tau.ab)$
, as required.
Case known expert As b already was known by a to be an expert,
![]() $\sigma\kern-0.8pt{.}ab \models \hat{K}_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
iff
$\sigma\kern-0.8pt{.}ab \models \hat{K}_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
iff
![]() $\sigma \models \hat{K}_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
, and therefore B was already distant-minimal. By inductive assumption, there is a
$\sigma \models \hat{K}_a (\mathit{Exp}_B \wedge \neg K_a\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B})$
, and therefore B was already distant-minimal. By inductive assumption, there is a
![]() $\tau\sim_a\sigma$
such that for all
$\tau\sim_a\sigma$
such that for all
![]() $c \in A{\setminus}B$
,
$c \in A{\setminus}B$
,
![]() $c(\sigma^{<c}) = c(\tau)$
and therefore also
$c(\sigma^{<c}) = c(\tau)$
and therefore also
![]() $c({(\sigma\kern-0.8pt{.}ab)}^{<c}) = c(\tau.ab)$
.
$c({(\sigma\kern-0.8pt{.}ab)}^{<c}) = c(\tau.ab)$
.
Case unknown close expert If b is an unknown close expert, magic is not lost as b cannot have been the sole unknown expert after
![]() $\sigma$
(see Lemma 17 and next case). So it is consistent to assume that
$\sigma$
(see Lemma 17 and next case). So it is consistent to assume that
![]() $\sigma\kern-0.8pt{.}ab\models K_a \mathsf{magic}$
. Given that, and Lemma 23, let
$\sigma\kern-0.8pt{.}ab\models K_a \mathsf{magic}$
. Given that, and Lemma 23, let
![]() $\tau$
be given with
$\tau$
be given with
![]() $\tau.ab\sim_a\sigma\kern-0.8pt{.}ab$
and
$\tau.ab\sim_a\sigma\kern-0.8pt{.}ab$
and
![]() $\tau.ab \models \mathit{Exp}_B \wedge \neg K_a \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. From
$\tau.ab \models \mathit{Exp}_B \wedge \neg K_a \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. From
![]() $\tau.ab\sim_a\sigma\kern-0.8pt{.}ab$
,
$\tau.ab\sim_a\sigma\kern-0.8pt{.}ab$
,
![]() $b(\tau)=b(\sigma)=A$
, and
$b(\tau)=b(\sigma)=A$
, and
![]() $\sigma\kern-0.8pt{.}ab \models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
, it follows that
$\sigma\kern-0.8pt{.}ab \models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
, it follows that
![]() $\tau\sim_a\sigma$
and also
$\tau\sim_a\sigma$
and also
![]() $\tau \models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. Furthermore, as
$\tau \models \mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
. Furthermore, as
![]() $\sigma\kern-0.8pt{.}ab \models \neg K_a \mathit{Exp}_B$
, also
$\sigma\kern-0.8pt{.}ab \models \neg K_a \mathit{Exp}_B$
, also
![]() $\sigma\models\neg K_a \mathit{Exp}_B$
. The set B must still be distant-minimal. Now using the inductive hypothesis, for all
$\sigma\models\neg K_a \mathit{Exp}_B$
. The set B must still be distant-minimal. Now using the inductive hypothesis, for all
![]() $c \in A{\setminus}B$
,
$c \in A{\setminus}B$
,
![]() $c(\sigma^{<c}) = c(\tau)$
. As none of these c is involved in call ab, also
$c(\sigma^{<c}) = c(\tau)$
. As none of these c is involved in call ab, also
![]() $c({(\sigma\kern-0.8pt{.}ab)}^{<c}) = c(\tau.ab)$
. This fulfills the proof requirements.
$c({(\sigma\kern-0.8pt{.}ab)}^{<c}) = c(\tau.ab)$
. This fulfills the proof requirements.
Case unknown distant expert Let now b be an unknown distant expert. By induction, we may assume that a considers it possible there is a distant-minimal
![]() $B\subseteq A$
and a
$B\subseteq A$
and a
![]() $\tau$
such that
$\tau$
such that
![]() $\sigma\sim_a\tau$
,
$\sigma\sim_a\tau$
,
![]() $b \in B$
the unique unknown expert (as B is distant-minimal and b is distant), and
$b \in B$
the unique unknown expert (as B is distant-minimal and b is distant), and
![]() $\tau\models \mathit{Exp}_B \wedge \neg K_a \mathit{Exp}_B \wedge \mathit{NExp}_{B{\setminus}A}$
. Therefore,
$\tau\models \mathit{Exp}_B \wedge \neg K_a \mathit{Exp}_B \wedge \mathit{NExp}_{B{\setminus}A}$
. Therefore,
![]() $\sigma\models K_a \mathit{Exp}_{B{-}b}$
. From
$\sigma\models K_a \mathit{Exp}_{B{-}b}$
. From
![]() $\sigma\sim_a\tau$
and
$\sigma\sim_a\tau$
and
![]() $b(\tau)=b(\sigma)=A$
, we obtain that
$b(\tau)=b(\sigma)=A$
, we obtain that
![]() $\sigma\kern-0.8pt{.}ab \sim_a \tau.ab$
. Also,
$\sigma\kern-0.8pt{.}ab \sim_a \tau.ab$
. Also,
![]() $\tau.ab\models\mathit{Exp}_B\wedge\mathit{NExp}_{B{\setminus}A}$
. From that and
$\tau.ab\models\mathit{Exp}_B\wedge\mathit{NExp}_{B{\setminus}A}$
. From that and
![]() $\sigma\models K_a \mathit{Exp}_{B{-}b}$
, we further obtain that
$\sigma\models K_a \mathit{Exp}_{B{-}b}$
, we further obtain that
![]() $\sigma\kern-0.8pt{.}ab \models K_a \mathit{Exp}_B$
, so that
$\sigma\kern-0.8pt{.}ab \models K_a \mathit{Exp}_B$
, so that
![]() $\sigma\kern-0.8pt{.}ab \models K_a\mathit{Exp}_B \wedge \hat{K}_a \mathit{NExp}_{A{\setminus}B}$
. Therefore,
$\sigma\kern-0.8pt{.}ab \models K_a\mathit{Exp}_B \wedge \hat{K}_a \mathit{NExp}_{A{\setminus}B}$
. Therefore,
![]() $\sigma\kern-0.8pt{.}ab \not \models K_a \mathsf{magic}$
(Lemma 17).
$\sigma\kern-0.8pt{.}ab \not \models K_a \mathsf{magic}$
(Lemma 17).
Corollary 28. Let
![]() $\sigma$
be given with
$\sigma$
be given with
![]() $\sigma\models K_a \mathsf{magic}$
. If b is an unknown distant expert,
$\sigma\models K_a \mathsf{magic}$
. If b is an unknown distant expert,
![]() $\sigma\kern-0.8pt{.}ab \not\models K_a \mathsf{magic}$
.
$\sigma\kern-0.8pt{.}ab \not\models K_a \mathsf{magic}$
.
In the magic call agent a learns that there are three experts, of which she only knows two. In each subsequent call to a non-expert, an unknown close expert, or an unknown distant expert, she learns that there is one more expert, whereas a subsequent call to a known expert makes no difference for the count. If magic holds, a subsequent call to an unknown distant expert destroys it. So as long as magic still holds, she keeps updating the counter until she knows that all distant agents but one are experts and remains uncertain which of two distant agents are experts. She may at that stage know or be ignorant about any number of close agents. If the next call is then with a distant non-expert, she is lucky.
In the following proposition, the condition that b,c are distant implies that if there is a non-empty
![]() $D \subseteq A$
such that
$D \subseteq A$
such that
![]() $\sigma^{<a}\models K_a \mathit{Exp}_D(A{-}b)$
or
$\sigma^{<a}\models K_a \mathit{Exp}_D(A{-}b)$
or
![]() $\sigma^{<a}\models K_a \mathit{Exp}_D(A{-}c)$
, then
$\sigma^{<a}\models K_a \mathit{Exp}_D(A{-}c)$
, then
![]() $c,d\notin D$
.
$c,d\notin D$
.
Proposition 29. Expert to non-expert with magic. An agent who is an expert is lucky iff she knows that all distant agents but one are experts and calls the non-expert.
Let all different
![]() $a,b,c \in A$
and
$a,b,c \in A$
and
![]() $\sigma$
be given and suppose
$\sigma$
be given and suppose
![]() $\sigma \models \mathit{Exp}_a$
,
$\sigma \models \mathit{Exp}_a$
,
![]() $\sigma \not\models \mathit{Exp}_c$
,
$\sigma \not\models \mathit{Exp}_c$
,
![]() $\sigma \not \models K_a\mathit{Exp}_b$
, and
$\sigma \not \models K_a\mathit{Exp}_b$
, and
![]() $\sigma\models K_a \mathsf{magic}$
.
$\sigma\models K_a \mathsf{magic}$
.
Then
![]() $\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
iff
$\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
iff
![]() $\sigma \models \mathit{Exp}_b$
,
$\sigma \models \mathit{Exp}_b$
,
![]() $\sigma \models K_a (\mathit{Exp}_b \vee \mathit{Exp}_c)$
, and b,c distant.
$\sigma \models K_a (\mathit{Exp}_b \vee \mathit{Exp}_c)$
, and b,c distant.
Proof. (
![]() $\Rightarrow$
) We show this by contraposition. We need to consider three cases.
$\Rightarrow$
) We show this by contraposition. We need to consider three cases.
Case 1: If
![]() $\sigma\not \models \mathit{Exp}_b$
, also
$\sigma\not \models \mathit{Exp}_b$
, also
![]() $\sigma\kern-0.8pt{.}ac\not\models\mathit{Exp}_b$
and therefore
$\sigma\kern-0.8pt{.}ac\not\models\mathit{Exp}_b$
and therefore
![]() $\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
.
Case 2: If b or c are close, the assumption of magic makes us derive a contradiction. Agent a is then uncertain about at most one distant agent. Suppose b is distant and c close. By magic (Lemma 27), there is a distant-minimal B containing b with
![]() $\sigma \models \mathit{Exp}_B \wedge \neg K_a \mathit{Exp}_B$
; however, satisfying such ignorance requires a distant-minimal C not containing b with
$\sigma \models \mathit{Exp}_B \wedge \neg K_a \mathit{Exp}_B$
; however, satisfying such ignorance requires a distant-minimal C not containing b with
![]() $\sigma \models \mathit{Exp}_C \wedge \neg K_a \mathit{Exp}_C$
, but as C is distant-minimal, it must contain a distant
$\sigma \models \mathit{Exp}_C \wedge \neg K_a \mathit{Exp}_C$
, but as C is distant-minimal, it must contain a distant
![]() $c \neq b$
. So a must be uncertain about at least two distant agents b,c, contradicting our assumption. This situation cannot exist if magic holds.
$c \neq b$
. So a must be uncertain about at least two distant agents b,c, contradicting our assumption. This situation cannot exist if magic holds.
Case 3: If
![]() $\sigma \not\models K_a (\mathit{Exp}_b \vee \mathit{Exp}_c)$
where b,c are distant, then a does not know that at most one distant agent is non-expert while remaining uncertain about two and therefore considers it possible that two or more distant agents are non-experts while remaining uncertain about three or more: Lemma 27. There is then a distant-minimal B of size at most
$\sigma \not\models K_a (\mathit{Exp}_b \vee \mathit{Exp}_c)$
where b,c are distant, then a does not know that at most one distant agent is non-expert while remaining uncertain about two and therefore considers it possible that two or more distant agents are non-experts while remaining uncertain about three or more: Lemma 27. There is then a distant-minimal B of size at most
![]() $|A|-2$
with
$|A|-2$
with
![]() $b,c \in A{\setminus}B$
and a
$b,c \in A{\setminus}B$
and a
![]() $\tau\sim_a\sigma$
with
$\tau\sim_a\sigma$
with
![]() $\tau\models\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
and in particular
$\tau\models\mathit{Exp}_B \wedge \mathit{NExp}_{A{\setminus}B}$
and in particular
![]() $b(\tau)=b(\sigma^{<b})$
and
$b(\tau)=b(\sigma^{<b})$
and
![]() $c(\tau)=c(\sigma^{<c})=c(\sigma)$
. Therefore,
$c(\tau)=c(\sigma^{<c})=c(\sigma)$
. Therefore,
![]() $\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. From that and
$\sigma\kern-0.8pt{.}ac\sim_a\tau.ac$
. From that and
![]() $\tau.ac\not\models\mathit{Exp}_b$
, we then obtain
$\tau.ac\not\models\mathit{Exp}_b$
, we then obtain
![]() $\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
.
$\sigma\kern-0.8pt{.}ac\not\models K_a \mathit{Exp}_b$
.
(
![]() $\Leftarrow$
) Assume
$\Leftarrow$
) Assume
![]() $\sigma \models \mathit{Exp}_b$
,
$\sigma \models \mathit{Exp}_b$
,
![]() $\sigma \models K_a(\mathit{Exp}_b \wedge \mathit{Exp}_b)$
and recall that we also assume that
$\sigma \models K_a(\mathit{Exp}_b \wedge \mathit{Exp}_b)$
and recall that we also assume that
![]() $\sigma \not\models \mathit{Exp}_c$
. Let
$\sigma \not\models \mathit{Exp}_c$
. Let
![]() $\tau'$
be such that
$\tau'$
be such that
![]() $\tau' \sim_a \sigma\kern-0.8pt{.}ac$
, then we may assume that
$\tau' \sim_a \sigma\kern-0.8pt{.}ac$
, then we may assume that
![]() $\tau$
has shape
$\tau$
has shape
![]() $\tau' = \tau.ac$
where
$\tau' = \tau.ac$
where
![]() $c(\tau)=c(\sigma)$
and
$c(\tau)=c(\sigma)$
and
![]() $\tau\sim_a\sigma$
. From
$\tau\sim_a\sigma$
. From
![]() $\tau\sim_a\sigma$
and
$\tau\sim_a\sigma$
and
![]() $\sigma \models K_a(\mathit{Exp}_b \vee \mathit{Exp}_b)$
, it follows that
$\sigma \models K_a(\mathit{Exp}_b \vee \mathit{Exp}_b)$
, it follows that
![]() $\tau \models \mathit{Exp}_b \vee \mathit{Exp}_b$
. From
$\tau \models \mathit{Exp}_b \vee \mathit{Exp}_b$
. From
![]() $\sigma \not\models \mathit{Exp}_c$
and
$\sigma \not\models \mathit{Exp}_c$
and
![]() $c(\tau)=c(\sigma)$
, it follows that
$c(\tau)=c(\sigma)$
, it follows that
![]() $\tau \not \models \mathit{Exp}_c$
. From
$\tau \not \models \mathit{Exp}_c$
. From
![]() $\tau \not \models \mathit{Exp}_c$
and
$\tau \not \models \mathit{Exp}_c$
and
![]() $\tau \models \mathit{Exp}_b \vee \mathit{Exp}_c$
, it follows that
$\tau \models \mathit{Exp}_b \vee \mathit{Exp}_c$
, it follows that
![]() $\tau \models \mathit{Exp}_b$
, and therefore also
$\tau \models \mathit{Exp}_b$
, and therefore also
![]() $\tau.ac \models \mathit{Exp}_b$
. As
$\tau.ac \models \mathit{Exp}_b$
. As
![]() $\tau$
was arbitrary, we get
$\tau$
was arbitrary, we get
![]() $\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
, as required.
$\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
, as required.
An expert a is lucky because she considers it possible that the agent she is lucky about was involved in a call with the agent of the magic call and that both then became expert. Therefore, she now considers it possible that she knows all the agents who are experts. Therefore:
Corollary 30. Given
![]() $\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
wherein expert a is lucky about b when calling non-expert c, magic is lost:
$\sigma\kern-0.8pt{.}ac \models K_a \mathit{Exp}_b$
wherein expert a is lucky about b when calling non-expert c, magic is lost:
![]() $\sigma\kern-0.8pt{.}ac \not \models K_a \mathsf{magic}$
.
$\sigma\kern-0.8pt{.}ac \not \models K_a \mathsf{magic}$
.
After the lucky call, agent a may remain uncertain whether an arbitrary number of close agents are experts. As she can no longer be lucky, she has to call them one by one to confirm whether they are experts (and if not they become experts in such calls), until she is a super expert. If there are no close agents, or if she already knew that all close agents are experts, she is a super expert after making the lucky call.
5.8 An agent can only be lucky once
In this short final subsection, we present one eye-catching result of our characterization efforts.
Theorem 1. An agent can only be lucky once.
Proof. Fix any agent a and distinguish two cases, depending on whether a is an expert at the first (and, as we will show, only) time she is lucky.
First case: If a is lucky as a non-expert, then she becomes an expert in the lucky call. Suppose a is lucky again later, then as an expert. This cannot happen in a call between a and another expert because by Proposition 13 expert-to-expert calls are never lucky. Hence, it must be when a calls a non-expert. However, Corollary 21 implies that we do not have magic, and therefore Proposition 22 implies that any call by a to a non-expert cannot be lucky.
Second case: Suppose a is already an expert when she is lucky the first time, and again suppose a is lucky again later. As in the first case, Proposition 13 rules out that a is lucky again when calling another expert, so it must be when a calls a non-expert. But now by Corollary 30, we also here do not have magic, and therefore Proposition 22 implies that also a call by a to any non-expert cannot be lucky.
As a was chosen arbitrarily, each agent can only be lucky once.
6. Second-order Shared Knowledge of all Secrets is Unsatisfiable
With all these preparations concerning lucky calls, we now can prove that second-order shared knowledge of all secrets is unsatisfiable (
![]() $\models\neg E\!E\!\mathit{Exp}_A$
, Theorem 2). Some additional lemmas are again required.
$\models\neg E\!E\!\mathit{Exp}_A$
, Theorem 2). Some additional lemmas are again required.
Lemma 31. An agent cannot become an expert and a super expert in the same call.
Proof. Suppose a becomes expert in ac, that is,
![]() $\sigma \not\models \mathit{Exp}_a$
and
$\sigma \not\models \mathit{Exp}_a$
and
![]() $\sigma\kern-0.8pt{.}ac \models Exp_a$
. We need to show that
$\sigma\kern-0.8pt{.}ac \models Exp_a$
. We need to show that
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_A$
. From
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_A$
. From
![]() $\sigma \not\models \mathit{Exp}_a$
, we know there must be a
$\sigma \not\models \mathit{Exp}_a$
, we know there must be a
![]() $d \in A$
such that
$d \in A$
such that
![]() $\sigma \models \lnot d_a$
. As there are at least four agents, there must be a
$\sigma \models \lnot d_a$
. As there are at least four agents, there must be a
![]() $b \not\in \{a,c,d\}$
. From
$b \not\in \{a,c,d\}$
. From
![]() $\sigma \models \lnot d_a$
, we get
$\sigma \models \lnot d_a$
, we get
![]() $\sigma \not\models \mathit{Exp}_a(A{-}b)$
and thus
$\sigma \not\models \mathit{Exp}_a(A{-}b)$
and thus
![]() $\sigma \not\models K_a \mathit{Exp}_{(A{-}b)}(A{-}b)$
. Now by Proposition 12, we have
$\sigma \not\models K_a \mathit{Exp}_{(A{-}b)}(A{-}b)$
. Now by Proposition 12, we have
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
. This implies
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_b$
. This implies
![]() $\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_A$
.
$\sigma\kern-0.8pt{.}ac \not\models K_a \mathit{Exp}_A$
.
In particular, if a becomes an expert by calling another non-expert she will not be lucky (Proposition 11), because she then only learns that two out of at least four agents are experts. However, note that we did not need to use Proposition 11 in the proof, but only Proposition 12.
We point out that Lemma 31 is the only place in this section where we need a result about lucky calls, and that we only use the characterization of lucky non-experts. The much more complex characterization of lucky experts is not needed in this section, but only to obtain results on optimality in Section 7.
Lemma 32. An agent becoming a super expert considers it possible that the other agent involved in that call did not become a super expert.
Proof. Let
![]() $\sigma\kern-0.8pt{.}ab$
be a call sequence wherein agent a becomes super expert in final call ab. From Lemma 31, we conclude that a was already expert after
$\sigma\kern-0.8pt{.}ab$
be a call sequence wherein agent a becomes super expert in final call ab. From Lemma 31, we conclude that a was already expert after
![]() $\sigma$
.
$\sigma$
.
Suppose that b became expert in the call ab. Then also from Lemma 31, we conclude that b did not become a super expert in the call ab. As a considers the actual call sequence possible, we infer that agent a then considers it possible that agent b is not a super expert after
![]() $\sigma\kern-0.8pt{.}ab$
.
$\sigma\kern-0.8pt{.}ab$
.
Thus, we can assume that b already was an expert after
![]() $\sigma$
. As a was an expert before call ab, a became a super expert by learning in call ab that b is an expert.
$\sigma$
. As a was an expert before call ab, a became a super expert by learning in call ab that b is an expert.
Suppose a considers it possible that non-expert b made a lucky call in
![]() $\sigma$
. The lucky call was not with a, as a would then already have known that b is an expert. So let that call be bc with some agent
$\sigma$
. The lucky call was not with a, as a would then already have known that b is an expert. So let that call be bc with some agent
![]() $c\neq a$
. Assume that in that call b also learns that d is an expert. If
$c\neq a$
. Assume that in that call b also learns that d is an expert. If
![]() $d=a$
, then (by Lemma 31) there must be an
$d=a$
, then (by Lemma 31) there must be an
![]() $e \neq c,a$
such that b is uncertain whether e is an expert, and this property is preserved in
$e \neq c,a$
such that b is uncertain whether e is an expert, and this property is preserved in
![]() $\sigma$
, as a considers it possible that b made no further calls. Otherwise, if
$\sigma$
, as a considers it possible that b made no further calls. Otherwise, if
![]() $d \neq a,c$
, then a considers it possible that the call instead of bc was bd. In call bd, agent b only learns that d is an expert (we recall that by Lemma 12 agent b must have been an
$d \neq a,c$
, then a considers it possible that the call instead of bc was bd. In call bd, agent b only learns that d is an expert (we recall that by Lemma 12 agent b must have been an
![]() $A{-}d$
super expert before that call) and does not learn that c is an expert. So a considers a call sequence possible wherein b was not lucky when he became expert, and therefore when becoming expert remained uncertain whether some other agent c is an expert.
$A{-}d$
super expert before that call) and does not learn that c is an expert. So a considers a call sequence possible wherein b was not lucky when he became expert, and therefore when becoming expert remained uncertain whether some other agent c is an expert.
We continue the argument by reasoning about this agent c.
Suppose a learnt that c is an expert in lucky call ad. Then a considers possible that all further calls involving c were instead involving d except for further calls ac. After this call sequence, b does not know that c is an expert, so b is not a super expert, so a considers possible after
![]() $\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
$\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
Now suppose that ac is the first call in
![]() $\sigma$
after which a knows that c is an expert. We now distinguish four cases by whether c and b are experts before the call ac.
$\sigma$
after which a knows that c is an expert. We now distinguish four cases by whether c and b are experts before the call ac.
1 Suppose c was already expert before that call ac.
1.1 If b became expert before call ac in call bd with
![]() $d \neq c$
, b was ignorant whether c is an expert after that call (we assumed bd was not lucky), replace bd by
$d \neq c$
, b was ignorant whether c is an expert after that call (we assumed bd was not lucky), replace bd by
![]() $bd.cd$
in the call sequence between bd and ac, and replace all further occurrences of c except in further calls ac by d. This call sequence is indistinguishable for a and preserves that b does not know that c is an expert (after final call ab). Therefore, a considers possible after
$bd.cd$
in the call sequence between bd and ac, and replace all further occurrences of c except in further calls ac by d. This call sequence is indistinguishable for a and preserves that b does not know that c is an expert (after final call ab). Therefore, a considers possible after
![]() $\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
$\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
1.2 If b became expert after call ac in call bd with
![]() $d \neq c$
, replace all subsequent occurrences of c except in calls ac by d. (We need not change any calls between ac and bd, as we assumed that b does not learn whether any other agent than d is an expert in call bd, which includes agent c.) Then b does not know after final call ab that c is an expert. Therefore, a considers possible after
$d \neq c$
, replace all subsequent occurrences of c except in calls ac by d. (We need not change any calls between ac and bd, as we assumed that b does not learn whether any other agent than d is an expert in call bd, which includes agent c.) Then b does not know after final call ab that c is an expert. Therefore, a considers possible after
![]() $\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
$\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
2 Suppose c became expert in that call ac.
2.1 If b became expert before ac in bd with
![]() $d \neq c$
, agent a considers possible that all further calls after ac involving c were instead by d, except for further occurrences of ac. We need not change any calls involving c between bd and ac: note that this cannot have been bc as that would have made c expert before ac contrary to our assumption. This call sequence preserves that b does not know whether c is an expert after final call ab. Therefore, a considers possible after
$d \neq c$
, agent a considers possible that all further calls after ac involving c were instead by d, except for further occurrences of ac. We need not change any calls involving c between bd and ac: note that this cannot have been bc as that would have made c expert before ac contrary to our assumption. This call sequence preserves that b does not know whether c is an expert after final call ab. Therefore, a considers possible after
![]() $\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
$\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
2.2 If b became expert after ac in bd with
![]() $d \neq c$
, agent a considers possible all further calls after bd involving c were instead by d except for future occurrences of ac. Now consider the calls involving c between ac and bd: we need not change any of those as we assumed that b only learnt that d is an expert in call bd. This call sequence preserves that b does not know whether c is an expert after final call ab. Therefore, a considers possible after
$d \neq c$
, agent a considers possible all further calls after bd involving c were instead by d except for future occurrences of ac. Now consider the calls involving c between ac and bd: we need not change any of those as we assumed that b only learnt that d is an expert in call bd. This call sequence preserves that b does not know whether c is an expert after final call ab. Therefore, a considers possible after
![]() $\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
$\sigma\kern-0.8pt{.}ab$
that b is not a super expert.
We have exhaustively investigated all cases and this ends the proof.
In Lemma 32, it is important to observe that the agent c that agent a remains uncertain about is different from the agent b involved in the call wherein she became a super expert. This will be used in Theorem 2.
Example 11. Recall the sequence
![]() $ab.cd.ac.bd.ad.bc.ab$
from Example 1 wherein a and b become super experts in the last call. It is indistinguishable for a from call sequence
$ab.cd.ac.bd.ad.bc.ab$
from Example 1 wherein a and b become super experts in the last call. It is indistinguishable for a from call sequence
![]() $ab.cd.ac.bd.ad.ab$
(where we deleted bc) after which b is not a super expert. Instead of deleting bc, we could also replace it by bd in the original sequence.
$ab.cd.ac.bd.ad.ab$
(where we deleted bc) after which b is not a super expert. Instead of deleting bc, we could also replace it by bd in the original sequence.
With Lemma 32, we can now prove the main result of this section.
Theorem 2.
![]() $E\!E\!\mathit{Exp}_A$
is unsatisfiable.
$E\!E\!\mathit{Exp}_A$
is unsatisfiable.
Proof. Let
![]() $\rho$
be an arbitrary call sequence. We show that
$\rho$
be an arbitrary call sequence. We show that
![]() $\rho \not \models E\!E\!\mathit{Exp}_A$
. If
$\rho \not \models E\!E\!\mathit{Exp}_A$
. If
![]() $\rho \not\models E\!\mathit{Exp}_A$
, then clearly
$\rho \not\models E\!\mathit{Exp}_A$
, then clearly
![]() $\rho \not\models E\!E\!\mathit{Exp}_A$
. Hence, we assume that
$\rho \not\models E\!E\!\mathit{Exp}_A$
. Hence, we assume that
![]() $\rho \models E\!\mathit{Exp}_A$
.
$\rho \models E\!\mathit{Exp}_A$
.
Consider any agent a becoming a super expert in
![]() $\rho$
; in other words, choose
$\rho$
; in other words, choose
![]() $\sigma$
and
$\sigma$
and
![]() $\tau$
such that
$\tau$
such that
![]() $\rho = \sigma\kern-0.8pt{.}ab.\tau$
where in call ab agent a becomes a super expert. We will show that
$\rho = \sigma\kern-0.8pt{.}ab.\tau$
where in call ab agent a becomes a super expert. We will show that
![]() $\rho \not \models K_a K_b \mathit{Exp}_c$
for some
$\rho \not \models K_a K_b \mathit{Exp}_c$
for some
![]() $c \in A$
.
$c \in A$
.
From Lemma 32, it follows that after
![]() $\sigma\kern-0.8pt{.}ab$
agent a considers possible a call sequence
$\sigma\kern-0.8pt{.}ab$
agent a considers possible a call sequence
![]() $\sigma'\kern-0.8pt{.}ab$
after which b is not a super expert. Therefore, b considers possible a call sequence
$\sigma'\kern-0.8pt{.}ab$
after which b is not a super expert. Therefore, b considers possible a call sequence
![]() $\sigma''\kern-0.8pt{.}ab$
that does not satisfy
$\sigma''\kern-0.8pt{.}ab$
that does not satisfy
![]() $\mathit{Exp}_A$
, that is,
$\mathit{Exp}_A$
, that is,
![]() $\sigma''\kern-0.8pt{.}ab$
does not satisfy
$\sigma''\kern-0.8pt{.}ab$
does not satisfy
![]() $\mathit{Exp}_c$
for some
$\mathit{Exp}_c$
for some
![]() $c \in A$
. Clearly, we must have that
$c \in A$
. Clearly, we must have that
![]() $c \neq a$
(because b learnt that a is an expert in the call ab). Formally, we have:
$c \neq a$
(because b learnt that a is an expert in the call ab). Formally, we have:
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma'\kern-0.8pt{.}ab$
and
$\sigma\kern-0.8pt{.}ab \sim_a \sigma'\kern-0.8pt{.}ab$
and
![]() $\sigma'\kern-0.8pt{.}ab \sim_b \sigma''\kern-0.8pt{.}ab$
and
$\sigma'\kern-0.8pt{.}ab \sim_b \sigma''\kern-0.8pt{.}ab$
and
![]() $\sigma''\kern-0.8pt{.}ab \models \neg \mathit{Exp}_c$
. The last implies
$\sigma''\kern-0.8pt{.}ab \models \neg \mathit{Exp}_c$
. The last implies
![]() $\sigma'' \models \neg \mathit{Exp}_c$
.
$\sigma'' \models \neg \mathit{Exp}_c$
.
The sequence
![]() $\sigma\kern-0.8pt{.}ab.\tau$
is indistinguishable for a from
$\sigma\kern-0.8pt{.}ab.\tau$
is indistinguishable for a from
![]() $\sigma\kern-0.8pt{.}ab.\tau'$
where
$\sigma\kern-0.8pt{.}ab.\tau'$
where
![]() $\tau'$
is
$\tau'$
is
![]() $\tau$
without all calls involving b but not a. This is because no secrets are exchanged in any call in
$\tau$
without all calls involving b but not a. This is because no secrets are exchanged in any call in
![]() $\tau$
, because all agents are already experts (because a is a super expert after
$\tau$
, because all agents are already experts (because a is a super expert after
![]() $\sigma\kern-0.8pt{.}ab$
).
$\sigma\kern-0.8pt{.}ab$
).
For the same reason,
![]() $\sigma\kern-0.8pt{.}ab.\tau'$
is indistinguishable for b from
$\sigma\kern-0.8pt{.}ab.\tau'$
is indistinguishable for b from
![]() $\sigma\kern-0.8pt{.}ab.\tau''$
where
$\sigma\kern-0.8pt{.}ab.\tau''$
where
![]() $\tau''$
is
$\tau''$
is
![]() $\tau'$
restricted to calls involving b. Call sequence
$\tau'$
restricted to calls involving b. Call sequence
![]() $\tau''$
is a finite and possibly empty sequence consisting only of calls ab. We can write
$\tau''$
is a finite and possibly empty sequence consisting only of calls ab. We can write
![]() ${ab}^n$
for that, where
${ab}^n$
for that, where
![]() $n \in \mathbb{N}$
is the number of occurrences of ab in
$n \in \mathbb{N}$
is the number of occurrences of ab in
![]() $\tau$
(and
$\tau$
(and
![]() $\tau'$
).
$\tau'$
).
First, from
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma\kern-0.8pt{.}ab$
(reflexivity of
$\sigma\kern-0.8pt{.}ab \sim_a \sigma\kern-0.8pt{.}ab$
(reflexivity of
![]() $\sim_a$
),
$\sim_a$
),
![]() $\tau \sim_a \tau'$
, and the fact that all are experts before
$\tau \sim_a \tau'$
, and the fact that all are experts before
![]() $\tau$
and
$\tau$
and
![]() $\tau'$
(so no new secrets are learnt in calls), we get
$\tau'$
(so no new secrets are learnt in calls), we get
![]() $\sigma\kern-0.8pt{.}ab.\tau \sim_a \sigma\kern-0.8pt{.}ab.\tau'$
. Then, from the assumption
$\sigma\kern-0.8pt{.}ab.\tau \sim_a \sigma\kern-0.8pt{.}ab.\tau'$
. Then, from the assumption
![]() $\sigma\kern-0.8pt{.}ab \sim_a \sigma'\kern-0.8pt{.}ab$
,
$\sigma\kern-0.8pt{.}ab \sim_a \sigma'\kern-0.8pt{.}ab$
,
![]() $\tau' \sim_a \tau'$
(reflexivity of
$\tau' \sim_a \tau'$
(reflexivity of
![]() $\sim_a$
again), and that all are experts before
$\sim_a$
again), and that all are experts before
![]() $\tau'$
, we get
$\tau'$
, we get
![]() $\sigma\kern-0.8pt{.}ab.\tau' \sim_a \sigma'\kern-0.8pt{.}ab.\tau'$
. Finally, from
$\sigma\kern-0.8pt{.}ab.\tau' \sim_a \sigma'\kern-0.8pt{.}ab.\tau'$
. Finally, from
![]() $\sigma\kern-0.8pt{.}ab.\tau \sim_a \sigma\kern-0.8pt{.}ab.\tau'$
and
$\sigma\kern-0.8pt{.}ab.\tau \sim_a \sigma\kern-0.8pt{.}ab.\tau'$
and
![]() $\sigma\kern-0.8pt{.}ab.\tau' \sim_a \sigma'\kern-0.8pt{.}ab.\tau'$
and transitivity of
$\sigma\kern-0.8pt{.}ab.\tau' \sim_a \sigma'\kern-0.8pt{.}ab.\tau'$
and transitivity of
![]() $\sim_a$
, we then get
$\sim_a$
, we then get
![]() $\sigma\kern-0.8pt{.}ab.\tau \sim_a \sigma'\kern-0.8pt{.}ab.\tau'$
.
$\sigma\kern-0.8pt{.}ab.\tau \sim_a \sigma'\kern-0.8pt{.}ab.\tau'$
.
Similarly, from
![]() $\sigma'\kern-0.8pt{.}ab \sim_b \sigma'\kern-0.8pt{.}ab$
and
$\sigma'\kern-0.8pt{.}ab \sim_b \sigma'\kern-0.8pt{.}ab$
and
![]() $\tau' \sim_b \tau''$
we get
$\tau' \sim_b \tau''$
we get
![]() $\sigma'\kern-0.8pt{.}ab.\tau' \sim_b \sigma'\kern-0.8pt{.}ab.\tau''$
, from
$\sigma'\kern-0.8pt{.}ab.\tau' \sim_b \sigma'\kern-0.8pt{.}ab.\tau''$
, from
![]() $\sigma'\kern-0.8pt{.}ab \sim_b \sigma''\kern-0.8pt{.}ab$
and
$\sigma'\kern-0.8pt{.}ab \sim_b \sigma''\kern-0.8pt{.}ab$
and
![]() $\tau'' \sim_b \tau''$
we get
$\tau'' \sim_b \tau''$
we get
![]() $\sigma'\kern-0.8pt{.}ab.\tau'' \sim_b \sigma''\kern-0.8pt{.}ab.\tau''$
(although c is not an expert in
$\sigma'\kern-0.8pt{.}ab.\tau'' \sim_b \sigma''\kern-0.8pt{.}ab.\tau''$
(although c is not an expert in
![]() $\sigma''$
, a and b are, so as above no new secrets are learnt in calls in
$\sigma''$
, a and b are, so as above no new secrets are learnt in calls in
![]() $\tau''$
), and therefore from both we obtain
$\tau''$
), and therefore from both we obtain
![]() $\sigma'\kern-0.8pt{.}ab.\tau' \sim_b \sigma''\kern-0.8pt{.}ab.\tau''$
.
$\sigma'\kern-0.8pt{.}ab.\tau' \sim_b \sigma''\kern-0.8pt{.}ab.\tau''$
.
From
![]() $\sigma'' \not\models \mathit{Exp}_c$
and
$\sigma'' \not\models \mathit{Exp}_c$
and
![]() $\sigma''\kern-0.8pt{.}ab.\tau'' = \sigma''\kern-0.8pt{.}ab^{n+1}$
, we obtain
$\sigma''\kern-0.8pt{.}ab.\tau'' = \sigma''\kern-0.8pt{.}ab^{n+1}$
, we obtain
![]() $\sigma''\kern-0.8pt{.}ab.\tau'' \not\models \mathit{Exp}_c$
. Finally, in view of the above
$\sigma''\kern-0.8pt{.}ab.\tau'' \not\models \mathit{Exp}_c$
. Finally, in view of the above
![]() $\sigma'\kern-0.8pt{.}ab.\tau' \not\models K_b \mathit{Exp}_c$
, and also
$\sigma'\kern-0.8pt{.}ab.\tau' \not\models K_b \mathit{Exp}_c$
, and also
![]() $\sigma\kern-0.8pt{.}ab.\tau \not\models K_a K_b \mathit{Exp}_c$
.
$\sigma\kern-0.8pt{.}ab.\tau \not\models K_a K_b \mathit{Exp}_c$
.
This implies
![]() $\rho \not \models E\!E\!\mathit{Exp}_A$
and because
$\rho \not \models E\!E\!\mathit{Exp}_A$
and because
![]() $\rho$
was an arbitrary call sequence, we have shown
$\rho$
was an arbitrary call sequence, we have shown
![]() $E\!E\!\mathit{Exp}_A$
must be unsatisfiable.
$E\!E\!\mathit{Exp}_A$
must be unsatisfiable.
In the proof above, the agent a who is a super expert can be chosen arbitrarily, as all agents become a super expert at some stage. We have therefore also shown the following, which is slightly stronger (proving that
![]() $E\!E\!\mathit{Exp}_A$
is unsatisfiable only requires that
$E\!E\!\mathit{Exp}_A$
is unsatisfiable only requires that
![]() $K_aE\!\mathit{Exp}_A$
is unsatisfiable for some agent).
$K_aE\!\mathit{Exp}_A$
is unsatisfiable for some agent).
Corollary 33. For all agents a the formula
![]() $K_a E\!\mathit{Exp}_A$
is unsatisfiable.
$K_a E\!\mathit{Exp}_A$
is unsatisfiable.
7. Optimality
In this section, we determine the minimum number of calls to reach
![]() $E\!\mathit{Exp}_A$
(everyone knows that everyone knows all secrets) and the minimum number of calls to reach
$E\!\mathit{Exp}_A$
(everyone knows that everyone knows all secrets) and the minimum number of calls to reach
![]() $K_a\mathit{Exp}_A$
(someone knows that everyone knows all secrets – namely agent a). Although it is easy to come up with optimal call sequences, it is nontrivial to prove that they are optimal, given the phenomenon of lucky calls.
$K_a\mathit{Exp}_A$
(someone knows that everyone knows all secrets – namely agent a). Although it is easy to come up with optimal call sequences, it is nontrivial to prove that they are optimal, given the phenomenon of lucky calls.
Lemma 34. If a is lucky about b then b has to call a for b to learn that a is an expert.
Proof. If a non-expert a is lucky about b, then a became expert in a call to a close agent c (
![]() $K_a \mathit{Exp}_{A{-}b}(A{-}b)$
was true before a became expert), where we recall that a learns in that lucky call that b must have become an expert by calling a close agent
$K_a \mathit{Exp}_{A{-}b}(A{-}b)$
was true before a became expert), where we recall that a learns in that lucky call that b must have become an expert by calling a close agent
![]() $d \in A{-}b$
, where d may have been c. We refer to the proof of Lemma 12 for details. As b became expert by calling another non-expert, magic does not hold after that call (Lemma 18), so it will not ever hold afterward (Lemma 20). So b cannot be subsequently lucky about a. Therefore, agent b has to call agent a in order to get to know that a is an expert.
$d \in A{-}b$
, where d may have been c. We refer to the proof of Lemma 12 for details. As b became expert by calling another non-expert, magic does not hold after that call (Lemma 18), so it will not ever hold afterward (Lemma 20). So b cannot be subsequently lucky about a. Therefore, agent b has to call agent a in order to get to know that a is an expert.
If an expert a is lucky about b, then a became expert in a magic call to an agent c, where, if the set of close agents is non-empty, c is close (
![]() $K_a \mathit{Exp}_D (A{-}d)$
is true before a became expert, where D are the close agents and where d may be b or another distant agent). In the lucky call, a learns that one of the two remaining far agents is a non-expert and that therefore the other far agent is an expert. Recalling the proof of Proposition 29 characterizing lucky experts, a learns in that call that b became an expert by calling non-expert c before the magic call ac, or by calling one or more close agents who subsequently called c. Either way, b became an expert in a call with another non-expert. We now proceed as in the other case. As b became expert by calling another non-expert, magic does not hold after that call (Lemma 18), so it will not ever hold afterward (Lemma 20). So b cannot be subsequently lucky about a. Therefore, agent b has to call agent a in order to get to know that a is an expert.
$K_a \mathit{Exp}_D (A{-}d)$
is true before a became expert, where D are the close agents and where d may be b or another distant agent). In the lucky call, a learns that one of the two remaining far agents is a non-expert and that therefore the other far agent is an expert. Recalling the proof of Proposition 29 characterizing lucky experts, a learns in that call that b became an expert by calling non-expert c before the magic call ac, or by calling one or more close agents who subsequently called c. Either way, b became an expert in a call with another non-expert. We now proceed as in the other case. As b became expert by calling another non-expert, magic does not hold after that call (Lemma 18), so it will not ever hold afterward (Lemma 20). So b cannot be subsequently lucky about a. Therefore, agent b has to call agent a in order to get to know that a is an expert.
Finally, we recall that an agent can only be lucky once, as a non-expert or as an expert (Theorem 1).
Theorem 3.
![]() $n-2+\binom{n}{2}$
calls are optimal to reach
$n-2+\binom{n}{2}$
calls are optimal to reach
![]() $E\!\mathit{Exp}_A$
.
$E\!\mathit{Exp}_A$
.
Proof. We show that at most
![]() $n-2+\binom{n}{2}$
calls are needed to reach
$n-2+\binom{n}{2}$
calls are needed to reach
![]() $E\!\mathit{Exp}_A$
(upper bound) and that at least
$E\!\mathit{Exp}_A$
(upper bound) and that at least
![]() $n-2+\binom{n}{2}$
calls are needed to reach
$n-2+\binom{n}{2}$
calls are needed to reach
![]() $E\!\mathit{Exp}_A$
(lower bound). As the lower bound is the upper bound,
$E\!\mathit{Exp}_A$
(lower bound). As the lower bound is the upper bound,
![]() $n-2+\binom{n}{2}$
is optimal.
$n-2+\binom{n}{2}$
is optimal.
Upper bound: Call sequences of length
![]() $n-2+\binom{n}{2}$
to reach
$n-2+\binom{n}{2}$
to reach
![]() $E\!\mathit{Exp}_A$
are given in van Ditmarsch et al. (Reference van Ditmarsch, Gattinger and Ramezanian2023, Prop. 16). A simple protocol to realize this goal is to extend a well-known gossip protocol to reach
$E\!\mathit{Exp}_A$
are given in van Ditmarsch et al. (Reference van Ditmarsch, Gattinger and Ramezanian2023, Prop. 16). A simple protocol to realize this goal is to extend a well-known gossip protocol to reach
![]() $\mathit{Exp}_A$
in
$\mathit{Exp}_A$
in
![]() $2n-4$
calls (an execution for four agents is found in Example 1). Choose four agents a,b,c,d and consider
$2n-4$
calls (an execution for four agents is found in Example 1). Choose four agents a,b,c,d and consider
![]() $ab.cd.ac.bd$
. Given one of those, say a, let a call all remaining
$ab.cd.ac.bd$
. Given one of those, say a, let a call all remaining
![]() $n-4$
agents before the four calls of
$n-4$
agents before the four calls of
![]() $ab.cd.ac.bd$
and let a make those
$ab.cd.ac.bd$
and let a make those
![]() $n-4$
calls again after those calls. In the first
$n-4$
calls again after those calls. In the first
![]() $n-2$
of these
$n-2$
of these
![]() $2n-4$
calls, none becomes an expert. In the second
$2n-4$
calls, none becomes an expert. In the second
![]() $n-2$
of these
$n-2$
of these
![]() $2n-4$
calls, everyone becomes an expert. These count toward the required
$2n-4$
calls, everyone becomes an expert. These count toward the required
![]() $\binom{n}{2}$
calls after which the callers are experts. Now execute the remaining
$\binom{n}{2}$
calls after which the callers are experts. Now execute the remaining
![]() $\binom{n}{2}$
calls.
$\binom{n}{2}$
calls.
Therefore, at most
![]() $n-2+\binom{n}{2}$
calls are needed to reach
$n-2+\binom{n}{2}$
calls are needed to reach
![]() $E\!\mathit{Exp}_A$
.
$E\!\mathit{Exp}_A$
.
Lower bound: It follows from Lemma 34 that whenever an agent a is lucky about an agent b, whether a is an expert or not in the lucky call, the call ab still has to be made for b to get to know that a is an expert. Therefore, all
![]() $\binom{n}{2}$
calls need to be made such that after a call both agents are experts (even though they may not have been experts before the call).
$\binom{n}{2}$
calls need to be made such that after a call both agents are experts (even though they may not have been experts before the call).
Also, the minimum number of calls for an agent to become an expert is
![]() $n-1$
: this is the minimum number of links to connect n points. Therefore, given such a sequence, the first
$n-1$
: this is the minimum number of links to connect n points. Therefore, given such a sequence, the first
![]() $n-2$
calls are not enough for any agent to become an expert, whereas in the final call
$n-2$
calls are not enough for any agent to become an expert, whereas in the final call
![]() $n-1$
of that sequence the calling agents become experts. That call counts as one of
$n-1$
of that sequence the calling agents become experts. That call counts as one of
![]() $\binom{n}{2}$
calls after which agents are experts.
$\binom{n}{2}$
calls after which agents are experts.
Therefore, at least
![]() $n-2+\binom{n}{2}$
calls are needed to reach
$n-2+\binom{n}{2}$
calls are needed to reach
![]() $E\!\mathit{Exp}_A$
.
$E\!\mathit{Exp}_A$
.
Theorem 4.
![]() $2n-3$
calls are optimal to reach
$2n-3$
calls are optimal to reach
![]() $K_a \mathit{Exp}_A$
.
$K_a \mathit{Exp}_A$
.
Proof. We show that at most
![]() $2n-3$
calls are needed to reach
$2n-3$
calls are needed to reach
![]() $K_a\mathit{Exp}_A$
(upper bound) and that at least
$K_a\mathit{Exp}_A$
(upper bound) and that at least
![]() $2n-3$
calls are needed to reach
$2n-3$
calls are needed to reach
![]() $K_a\mathit{Exp}_A$
(lower bound). As the lower bound is the upper bound,
$K_a\mathit{Exp}_A$
(lower bound). As the lower bound is the upper bound,
![]() $2n-3$
is optimal.
$2n-3$
is optimal.
Upper bound: In van Ditmarsch et al. (Reference van Ditmarsch, Gattinger and Ramezanian2023, Prop. 15), it is shown that
![]() $2n-3$
calls are sufficient to make an agent a super expert. A very simple protocol to realize this goal is to let an agent a first call all other agents (
$2n-3$
calls are sufficient to make an agent a super expert. A very simple protocol to realize this goal is to let an agent a first call all other agents (
![]() $n-1$
calls) and then call all other agents again, except for the last one in the first round (
$n-1$
calls) and then call all other agents again, except for the last one in the first round (
![]() $n-2$
calls). Altogether these are
$n-2$
calls). Altogether these are
![]() $2n-3$
calls.
$2n-3$
calls.
Therefore, at most
![]() $2n-3$
calls are needed to reach
$2n-3$
calls are needed to reach
![]() $K_a\mathit{Exp}_a$
.
$K_a\mathit{Exp}_a$
.
Lower bound: The proof is by induction on n (for
![]() $n \geq 4$
).
$n \geq 4$
).
Base case
For the base case with
![]() $n=4$
agents, we use the model checker GoMoChe (Gattinger Reference Gattinger2023) to show that there is no sequence of
$n=4$
agents, we use the model checker GoMoChe (Gattinger Reference Gattinger2023) to show that there is no sequence of
![]() $2n - 4 = 4$
calls that reaches
$2n - 4 = 4$
calls that reaches
![]() $K_a \mathit{Exp}_A$
. The following command checks all the
$K_a \mathit{Exp}_A$
. The following command checks all the
![]() $12^4 = 20736$
relevant sequences in less than 1 minute:
$12^4 = 20736$
relevant sequences in less than 1 minute:
We refer to van Ditmarsch et al. (Reference van Ditmarsch, Gattinger and Ramezanian2023) for further examples and for instructions on how to use GoMoChe.
Inductive case
For the inductive step, we distinguish cases based on whether a is lucky or not and split the lucky case based on whether a is an expert or not when making the lucky call.
1.1 If a is lucky as a non-expert, she must be a super expert for all agents except one agent, b. We now use the inductive hypothesis that this requires
![]() $2(n-1)-3$
calls. Recalling Lemma 12 at least two more calls are needed after that: a call between an agent
$2(n-1)-3$
calls. Recalling Lemma 12 at least two more calls are needed after that: a call between an agent
![]() $c \neq a,b$
and agent b, followed by the call between a and c, after which a knows that a,b,c are experts. As there are at least four agents, at least one more call is needed for a to become a super expert. Altogether this makes
$c \neq a,b$
and agent b, followed by the call between a and c, after which a knows that a,b,c are experts. As there are at least four agents, at least one more call is needed for a to become a super expert. Altogether this makes
![]() $2(n-1)-3+2+1=2n-2$
calls. Therefore, this cannot be done in
$2(n-1)-3+2+1=2n-2$
calls. Therefore, this cannot be done in
![]() $2n-4$
calls.
$2n-4$
calls.
1.2 If a is lucky as an expert, we recall the circumstances needed for that to happen. First, a must have become an expert in a magic call ad to an agent d who already was an expert. This requires
![]() $n-1$
calls for d to become an expert plus one for the magic call ad. Second, the proof of Proposition 29 (including the lemmas on which it depends, and see also Example 8) demonstrated that at least
$n-1$
calls for d to become an expert plus one for the magic call ad. Second, the proof of Proposition 29 (including the lemmas on which it depends, and see also Example 8) demonstrated that at least
![]() $n-3$
subsequent calls to non-experts or close experts are then needed for a to be lucky in the final call. This makes
$n-3$
subsequent calls to non-experts or close experts are then needed for a to be lucky in the final call. This makes
![]() $(n-1) +1 + (n-3) = 2n-3$
calls. Therefore, this cannot be done in
$(n-1) +1 + (n-3) = 2n-3$
calls. Therefore, this cannot be done in
![]() $2n-4$
calls.
Footnote 4
$2n-4$
calls.
Footnote 4
2 If a is not lucky, we can proceed as follows. We recall that
![]() $2n-4$
calls are needed for all agents to become experts (Tijdeman Reference Tijdeman1971).
$2n-4$
calls are needed for all agents to become experts (Tijdeman Reference Tijdeman1971).
As an agent cannot become an expert and a super expert in the same call (Lemma 31), we therefore only need to show that in any such a call sequence, if the final call involves an agent who already is an expert, that agent cannot become a super expert in that call.
We name the calls by their order in the call sequence.
Assume toward a contradiction that agent a becomes a super expert in the final call
![]() $2n-4$
of the sequence. Note this call must involve a non-expert b (otherwise, it could have been deleted).
$2n-4$
of the sequence. Note this call must involve a non-expert b (otherwise, it could have been deleted).
Consider the penultimate call
![]() $2n-5$
. Some agent must become an expert in call
$2n-5$
. Some agent must become an expert in call
![]() $2n-5$
(otherwise it could have been deleted). If a is not involved in call
$2n-5$
(otherwise it could have been deleted). If a is not involved in call
![]() $2n-5$
, neither agent in call
$2n-5$
, neither agent in call
![]() $2n-5$
is also involved in the final call
$2n-5$
is also involved in the final call
![]() $2n-4$
. However, as call
$2n-4$
. However, as call
![]() $2n-5$
does not involve a, a considers it possible that call
$2n-5$
does not involve a, a considers it possible that call
![]() $2n-5$
did not take place, and therefore a cannot know that everybody is an expert. Therefore, a must also be involved in call
$2n-5$
did not take place, and therefore a cannot know that everybody is an expert. Therefore, a must also be involved in call
![]() $2n-5$
.
$2n-5$
.
If a was not an expert before call
![]() $2n-5$
, she would have had to make at least three calls, including call
$2n-5$
, she would have had to make at least three calls, including call
![]() $2n-5$
to become a super expert: a is not lucky, and there are at least four agents; and after call
$2n-5$
to become a super expert: a is not lucky, and there are at least four agents; and after call
![]() $2n-5$
agent a knows that there are two experts and remains uncertain whether the remaining agents, of which there are at least two, are experts. She therefore has to make two more call. But only one is vailable to her. So a must have been an expert before call
$2n-5$
agent a knows that there are two experts and remains uncertain whether the remaining agents, of which there are at least two, are experts. She therefore has to make two more call. But only one is vailable to her. So a must have been an expert before call
![]() $2n-5$
.
$2n-5$
.
By iterating this argument, we can conclude that a must have been involved in the final
![]() $n-1$
calls of the sequence of
$n-1$
calls of the sequence of
![]() $2n-4$
calls and becomes an expert in the first of those. On the other hand,
$2n-4$
calls and becomes an expert in the first of those. On the other hand,
![]() $n-1$
calls are needed for a to become an expert (to connect n points we need at least
$n-1$
calls are needed for a to become an expert (to connect n points we need at least
![]() $n-1$
links). This requires
$n-1$
links). This requires
![]() $(n-1)-1+(n-1) = 2n-3$
calls (the call wherein a becomes an expert is the first of the final
$(n-1)-1+(n-1) = 2n-3$
calls (the call wherein a becomes an expert is the first of the final
![]() $n-1$
calls to all other agents), in contradiction to our assumption that the sequence contains
$n-1$
calls to all other agents), in contradiction to our assumption that the sequence contains
![]() $2n-4$
calls.
$2n-4$
calls.
Therefore, this cannot be done in
![]() $2n-4$
calls.
$2n-4$
calls.
8. Conclusion
We have shown that “everyone knows that everyone knows all secrets” (
![]() $E\!\mathit{Exp}_A$
) is the maximum level of shared knowledge of all secrets that can be reached in asynchronous gossip. In other words, “everyone knows that everyone knows that everyone knows all secrets” (
$E\!\mathit{Exp}_A$
) is the maximum level of shared knowledge of all secrets that can be reached in asynchronous gossip. In other words, “everyone knows that everyone knows that everyone knows all secrets” (
![]() $E\!E\!\mathit{Exp}_A$
) is unreachable. We have also shown that
$E\!E\!\mathit{Exp}_A$
) is unreachable. We have also shown that
![]() $n-2 +\binom{n}{2}$
calls are optimal to reach this epistemic goal
$n-2 +\binom{n}{2}$
calls are optimal to reach this epistemic goal
![]() $E\!\mathit{Exp}_A$
and that
$E\!\mathit{Exp}_A$
and that
![]() $2n-3$
calls are optimal to reach the goal “some agent knows that everyone knows all secrets” (
$2n-3$
calls are optimal to reach the goal “some agent knows that everyone knows all secrets” (
![]() $K_a\mathit{Exp}_A$
).
$K_a\mathit{Exp}_A$
).
Acknowledgements
We thank the reviewers and express our deep gratitude for their detailed and helpful comments. Our thanks also go to the editors for this special issue. We thank Otto de Jong for pointing out that the proof of Theorem 2 also shows that
![]() $K_a E\!\mathit{Exp}_A$
is not satisfiable, which we previously thought to be an open question.
$K_a E\!\mathit{Exp}_A$
is not satisfiable, which we previously thought to be an open question.
Competing interests
The authors declare none.