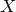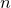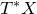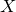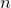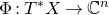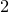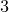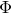1. Introduction
Let
![]() $X\subset \mathbb{P}^{n+2}_{\mathbb{C}}$
be a smooth
$X\subset \mathbb{P}^{n+2}_{\mathbb{C}}$
be a smooth
![]() $n$
-dimensional complete intersection of two quadrics, with
$n$
-dimensional complete intersection of two quadrics, with
![]() $n\geq 2$
, and let
$n\geq 2$
, and let
![]() $T^*X$
be its cotangent bundle. The
$T^*X$
be its cotangent bundle. The
![]() $\mathbb{C}$
-algebra
$\mathbb{C}$
-algebra
![]() $H^0(T^*X,\mathscr{O}_{T^*X})$
is canonically isomorphic to the algebra of symmetric tensors
$H^0(T^*X,\mathscr{O}_{T^*X})$
is canonically isomorphic to the algebra of symmetric tensors
![]() $H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X )$
. Recall that
$H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X )$
. Recall that
![]() $T^*X$
carries a canonical symplectic structure. Our main result is the following theorem:
$T^*X$
carries a canonical symplectic structure. Our main result is the following theorem:
Theorem 1.1.
(a) The vector space
![]() $W:=H^0(X,\mathsf{S}^{2}T_X )$
has dimension
$W:=H^0(X,\mathsf{S}^{2}T_X )$
has dimension
![]() $n$
, and the natural map
$n$
, and the natural map
![]() $\mathsf{S}^{\scriptscriptstyle \bullet } W\rightarrow H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X )$
is an isomorphism.
$\mathsf{S}^{\scriptscriptstyle \bullet } W\rightarrow H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X )$
is an isomorphism.
(b) The corresponding map,
![]() $\Phi : T^*X\rightarrow W^*\cong \mathbb{C}^n$
, is a Lagrangian fibration.
$\Phi : T^*X\rightarrow W^*\cong \mathbb{C}^n$
, is a Lagrangian fibration.
(c) When
![]() $X$
is general, the general fiber of
$X$
is general, the general fiber of
![]() $\Phi$
is of the form
$\Phi$
is of the form
![]() $A\smallsetminus Z$
, where
$A\smallsetminus Z$
, where
![]() $A$
is an abelian variety and
$A$
is an abelian variety and
![]() $\mathrm{codim}\ Z\geq 2$
.
$\mathrm{codim}\ Z\geq 2$
.
We will give a precise geometric description of the map
![]() $\Phi$
and of the abelian variety
$\Phi$
and of the abelian variety
![]() $A$
in Sections 4 and 5.
$A$
in Sections 4 and 5.
1.1 Comments
(1) For
![]() $n=2$
, (a) follows from Theorem 5.1 in [Reference De Oliveira and LangdonDOL19], while (b) and (c) are proved in [Reference Kim and LeeKL22]. The proof is based on the isomorphism
$n=2$
, (a) follows from Theorem 5.1 in [Reference De Oliveira and LangdonDOL19], while (b) and (c) are proved in [Reference Kim and LeeKL22]. The proof is based on the isomorphism
![]() $T_X\cong \Omega ^1_X(1)$
. The theorem also follows from the fact that
$T_X\cong \Omega ^1_X(1)$
. The theorem also follows from the fact that
![]() $X$
is a moduli space for parabolic rank 2 bundles on
$X$
is a moduli space for parabolic rank 2 bundles on
![]() $\mathbb{P}^1$
[Reference CasagrandeCas15], so
$\mathbb{P}^1$
[Reference CasagrandeCas15], so
![]() $\Phi :T^*X\rightarrow \mathbb{C}^2$
is identified to the Hitchin fibration (see [Reference Biswas, Holla and KumarBHK10]).
$\Phi :T^*X\rightarrow \mathbb{C}^2$
is identified to the Hitchin fibration (see [Reference Biswas, Holla and KumarBHK10]).
For
![]() $n=3$
,
$n=3$
,
![]() $X$
is isomorphic to the moduli space of vector bundles of rank 2 and fixed determinant of odd degree [Reference NewsteadNew68]; again, the theorem follows from the properties of the Hitchin fibration (see Section 2). It would be interesting to have a modular interpretation of
$X$
is isomorphic to the moduli space of vector bundles of rank 2 and fixed determinant of odd degree [Reference NewsteadNew68]; again, the theorem follows from the properties of the Hitchin fibration (see Section 2). It would be interesting to have a modular interpretation of
![]() $\Phi$
for
$\Phi$
for
![]() $n \geq 4$
. Note that the Hitchin map for
$n \geq 4$
. Note that the Hitchin map for
![]() $G$
-bundles is homogeneous quadratic only when
$G$
-bundles is homogeneous quadratic only when
![]() $G$
is
$G$
is
![]() $\mathrm{SL}(2)$
or a product of copies of
$\mathrm{SL}(2)$
or a product of copies of
![]() $\mathrm{SL}(2)$
, so this limits the possibilities of using it.
$\mathrm{SL}(2)$
, so this limits the possibilities of using it.
(2) The map
![]() $\Phi$
is an example of an algebraically completely integrable system; see Remark 5.1. There is an abundant literature on such systems; see, for instance, [Reference AudinA96].
$\Phi$
is an example of an algebraically completely integrable system; see Remark 5.1. There is an abundant literature on such systems; see, for instance, [Reference AudinA96].
A classical example, the geodesic flow on an ellipsoid, is discussed in detail in [Reference KnörrerK80]. The corresponding Lagrangian fibration takes place on the cotangent bundle of one quadric; it is not related to our
![]() $\Phi$
. However, some of the tools we use in Sections 4 and 5, in particular the variety
$\Phi$
. However, some of the tools we use in Sections 4 and 5, in particular the variety
![]() $\mathscr{X}$
and the family of planes
$\mathscr{X}$
and the family of planes
![]() $\mathscr{F}$
, appear already in [Reference KnörrerK80] (with a different purpose).
$\mathscr{F}$
, appear already in [Reference KnörrerK80] (with a different purpose).
(3) Such a situation is rather exceptional: Most varieties do not admit nonzero symmetric tensors (for instance, hypersurfaces of degree
![]() $\geq 3$
[Reference Liu and ShaoHLS22]); when they do, even for varieties as simple as quadrics, the algebra of symmetric tensors is fairly complicated (see, for instance, [Reference Beauville and LiuBLi24]). We do not have a conceptual explanation for the particularly simple behavior in our case.
$\geq 3$
[Reference Liu and ShaoHLS22]); when they do, even for varieties as simple as quadrics, the algebra of symmetric tensors is fairly complicated (see, for instance, [Reference Beauville and LiuBLi24]). We do not have a conceptual explanation for the particularly simple behavior in our case.
(4) For
![]() $n= 2$
or
$n= 2$
or
![]() $3$
, the generality assumption on
$3$
, the generality assumption on
![]() $X$
in (c) is unnecessary. It seems likely that this is the case for all
$X$
in (c) is unnecessary. It seems likely that this is the case for all
![]() $n$
, but our method does not allow us to make that conclusion.
$n$
, but our method does not allow us to make that conclusion.
1.2 Strategy
We will first treat the case
![]() $n=3$
, which is independent of the rest of this article (Section 2). For the general case, we will develop two different approaches. In the first one we exhibit a natural
$n=3$
, which is independent of the rest of this article (Section 2). For the general case, we will develop two different approaches. In the first one we exhibit a natural
![]() $n$
-dimensional subspace
$n$
-dimensional subspace
![]() $W\subset H^0(X,\mathsf{S}^2T_X)$
, from which we deduce a map
$W\subset H^0(X,\mathsf{S}^2T_X)$
, from which we deduce a map
![]() $\Phi :T^*X\rightarrow W^*\cong \mathbb{C}^n$
(Section 3). We then show that
$\Phi :T^*X\rightarrow W^*\cong \mathbb{C}^n$
(Section 3). We then show that
![]() $\Phi$
has the required properties, which implies (a), (b) and (c) for general
$\Phi$
has the required properties, which implies (a), (b) and (c) for general
![]() $X$
(5.1). In the second approach (Section 7), we directly prove (a) for all smooth X, by realizing
$X$
(5.1). In the second approach (Section 7), we directly prove (a) for all smooth X, by realizing
![]() $X$
as a double covering of a quadric.
$X$
as a double covering of a quadric.
1.3 Notations
Throughout this article,
![]() $X$
will be a smooth complete intersection of two quadrics in
$X$
will be a smooth complete intersection of two quadrics in
![]() $\mathbb{P}^{n+2}$
, with
$\mathbb{P}^{n+2}$
, with
![]() $n\geq 2$
. We denote by
$n\geq 2$
. We denote by
![]() $T^*X$
its cotangent bundle and by
$T^*X$
its cotangent bundle and by
![]() $\mathbb{P} T^*X$
its projectivisation in the geometric sense (not in the Grothendieck sense). If
$\mathbb{P} T^*X$
its projectivisation in the geometric sense (not in the Grothendieck sense). If
![]() $V$
is a vector space, we denote by
$V$
is a vector space, we denote by
![]() $\mathbb{P}(V)$
the associated projective space
$\mathbb{P}(V)$
the associated projective space
![]() $V\smallsetminus \{0\}/\mathbb{C}^*$
parametrising 1-dimensional subspaces of
$V\smallsetminus \{0\}/\mathbb{C}^*$
parametrising 1-dimensional subspaces of
![]() $V$
.
$V$
.
2. The case
 $\boldsymbol{{n}} \textbf{=} \textbf{3}$
$\boldsymbol{{n}} \textbf{=} \textbf{3}$
In this section we show how our general results can be obtained in the case
![]() $n=3$
by interpreting
$n=3$
by interpreting
![]() $X$
as a moduli space.
$X$
as a moduli space.
As in Section 4.1 below, we associate to
![]() $X$
a genus 2 curve
$X$
a genus 2 curve
![]() $C$
such that the variety of lines in
$C$
such that the variety of lines in
![]() $X$
is isomorphic to
$X$
is isomorphic to
![]() $JC$
. Let us fix a line bundle
$JC$
. Let us fix a line bundle
![]() $N$
on
$N$
on
![]() $C$
of degree
$C$
of degree
![]() $1$
; then
$1$
; then
![]() $X$
is isomorphic to the moduli space
$X$
is isomorphic to the moduli space
![]() $\mathscr{M}$
of rank 2 stable vector bundles on
$\mathscr{M}$
of rank 2 stable vector bundles on
![]() $C$
with determinant
$C$
with determinant
![]() $N$
[Reference NewsteadNew68]. The cotangent bundle
$N$
[Reference NewsteadNew68]. The cotangent bundle
![]() $T^*\mathscr{M}$
is naturally identified with the moduli space of Higgs bundles; that is, pairs
$T^*\mathscr{M}$
is naturally identified with the moduli space of Higgs bundles; that is, pairs
![]() $(E,u)$
with
$(E,u)$
with
![]() $E\in \mathscr{M}$
and
$E\in \mathscr{M}$
and
![]() $u:E \rightarrow E\otimes K_C$
a homomorphism with
$u:E \rightarrow E\otimes K_C$
a homomorphism with
![]() $\mathrm{Tr}u=0$
. The Hitchin map
$\mathrm{Tr}u=0$
. The Hitchin map
![]() $\Phi : T^*\mathscr{M}\rightarrow H^0(K_C^2)$
associates to a pair
$\Phi : T^*\mathscr{M}\rightarrow H^0(K_C^2)$
associates to a pair
![]() $(E,u)$
the section
$(E,u)$
the section
![]() ${\det u}$
of
${\det u}$
of
![]() $K_C^2$
. It is a Lagrangian fibration [Reference HitchinHit87].
$K_C^2$
. It is a Lagrangian fibration [Reference HitchinHit87].
Let
![]() $\omega \in H^0(K_C^2)$
. We assume in what follows that
$\omega \in H^0(K_C^2)$
. We assume in what follows that
![]() $\omega$
vanishes at
$\omega$
vanishes at
![]() $4$
distinct points. Let
$4$
distinct points. Let
![]() $C_{\omega }$
be the curve in the cotangent bundle
$C_{\omega }$
be the curve in the cotangent bundle
![]() $T^*C$
defined by
$T^*C$
defined by
![]() $z^2=\omega$
. The projection
$z^2=\omega$
. The projection
![]() $\pi :C_{\omega }\rightarrow C$
is a double covering branched along
$\pi :C_{\omega }\rightarrow C$
is a double covering branched along
![]() $\mathrm{div}(\omega )$
, and
$\mathrm{div}(\omega )$
, and
![]() $C_{\omega }$
is a smooth curve of genus 5. Let
$C_{\omega }$
is a smooth curve of genus 5. Let
![]() $P$
be the Prym variety associated to
$P$
be the Prym variety associated to
![]() $\pi$
, that is, the kernel of the norm map
$\pi$
, that is, the kernel of the norm map
![]() $\mathrm{Nm}:JC_{\omega }\rightarrow JC$
; it is a 3-dimensional abelian variety.
$\mathrm{Nm}:JC_{\omega }\rightarrow JC$
; it is a 3-dimensional abelian variety.
Proposition 2.1.
The fibre
![]() $\Phi ^{-1}(\omega )$
is isomorphic to the complement of a curve in
$\Phi ^{-1}(\omega )$
is isomorphic to the complement of a curve in
![]() $P$
.
$P$
.
Proof. Recall that the map
![]() $L\mapsto \pi _*L$
establishes a bijective correspondence between line bundles on
$L\mapsto \pi _*L$
establishes a bijective correspondence between line bundles on
![]() $C_{\omega }$
and rank 2 vector bundles
$C_{\omega }$
and rank 2 vector bundles
![]() $E$
on
$E$
on
![]() $C$
endowed with a homomorphism
$C$
endowed with a homomorphism
![]() $u:E\rightarrow E\otimes K_C$
such that
$u:E\rightarrow E\otimes K_C$
such that
![]() $u^2=\omega \cdot \mathrm{Id}_E$
or, equivalently,
$u^2=\omega \cdot \mathrm{Id}_E$
or, equivalently,
![]() $\mathrm{Tr}u=0$
and
$\mathrm{Tr}u=0$
and
![]() $\det u=\omega$
(see, for instance, [Reference Beauville, Narasimhan and RamananBNR89]). To get
$\det u=\omega$
(see, for instance, [Reference Beauville, Narasimhan and RamananBNR89]). To get
![]() $(E,u)$
in
$(E,u)$
in
![]() $\Phi ^{-1}(\omega )$
, we have to impose
$\Phi ^{-1}(\omega )$
, we have to impose
![]() $\det E= N$
and
$\det E= N$
and
![]() $E$
stable. Since
$E$
stable. Since
![]() $\det \pi _*L= \mathrm{Nm}(L)\otimes K_C^{-1}$
, the first condition means that
$\det \pi _*L= \mathrm{Nm}(L)\otimes K_C^{-1}$
, the first condition means that
![]() $L$
belongs to the translate
$L$
belongs to the translate
![]() $P_N:=\mathrm{Nm}^{-1}(K_C\otimes N)$
of
$P_N:=\mathrm{Nm}^{-1}(K_C\otimes N)$
of
![]() $P$
.
$P$
.
Then the vector bundle
![]() $\pi _*L$
is unstable if and only if it contains an invertible subsheaf
$\pi _*L$
is unstable if and only if it contains an invertible subsheaf
![]() $M$
of degree 1; this is equivalent to saying that there is a nonzero map
$M$
of degree 1; this is equivalent to saying that there is a nonzero map
![]() $\pi ^*M\rightarrow L$
; that is,
$\pi ^*M\rightarrow L$
; that is,
![]() $L=\pi ^*M(p)$
for some point
$L=\pi ^*M(p)$
for some point
![]() $p\in C_{\omega }$
. The condition
$p\in C_{\omega }$
. The condition
![]() $L\in P_N$
means that
$L\in P_N$
means that
![]() $M^{2}(\pi (p))=K_C\otimes N$
, so
$M^{2}(\pi (p))=K_C\otimes N$
, so
![]() $M$
is determined by
$M$
is determined by
![]() $p$
up to the 2-torsion of
$p$
up to the 2-torsion of
![]() $JC$
. Thus the locus of line bundles
$JC$
. Thus the locus of line bundles
![]() $L\in P_N$
such that
$L\in P_N$
such that
![]() $\pi _*L$
is unstable is a curve.
$\pi _*L$
is unstable is a curve.
Let
![]() $\rho :C\rightarrow \mathbb{P}^1$
be the canonical double covering, with
$\rho :C\rightarrow \mathbb{P}^1$
be the canonical double covering, with
![]() $B\subset \mathbb{P}^1$
its branch locus. Since the homomorphism
$B\subset \mathbb{P}^1$
its branch locus. Since the homomorphism
![]() $\mathsf{S}^2H^0(K_C)\rightarrow H^0(K_C^{2})$
is surjective, the divisor of
$\mathsf{S}^2H^0(K_C)\rightarrow H^0(K_C^{2})$
is surjective, the divisor of
![]() $\omega$
is of the form
$\omega$
is of the form
![]() $\rho ^*(p+q)$
, for some
$\rho ^*(p+q)$
, for some
![]() $p,q\in \mathbb{P}^1$
; by assumption, we have
$p,q\in \mathbb{P}^1$
; by assumption, we have
![]() $p\neq q$
and
$p\neq q$
and
![]() $p,q\notin B$
.
$p,q\notin B$
.
Proposition 2.2.
Let
![]() $\Gamma$
be the double covering of
$\Gamma$
be the double covering of
![]() $\mathbb{P}^1$
branched along
$\mathbb{P}^1$
branched along
![]() $B\cup \{p,q\}$
. There is an exact sequence
$B\cup \{p,q\}$
. There is an exact sequence
Proof. Let
![]() $\chi :\mathbb{P}^1\rightarrow \mathbb{P}^1$
be the double covering branched along
$\chi :\mathbb{P}^1\rightarrow \mathbb{P}^1$
be the double covering branched along
![]() $\{p,q\}$
. Since
$\{p,q\}$
. Since
![]() $\mathrm{div}(\omega ) =\rho ^*(p+q)$
, there is a cartesian diagram of double coverings
$\mathrm{div}(\omega ) =\rho ^*(p+q)$
, there is a cartesian diagram of double coverings

which gives rise to two commuting involutions
![]() $\sigma, \tau$
of
$\sigma, \tau$
of
![]() $C_{\omega }$
, exchanging the two sheets of
$C_{\omega }$
, exchanging the two sheets of
![]() $\pi$
and
$\pi$
and
![]() $\xi$
, respectively. The field of rational functions on
$\xi$
, respectively. The field of rational functions on
![]() $C_{\omega }$
is
$C_{\omega }$
is
where
![]() $f$
and
$f$
and
![]() $g$
are polynomials with
$g$
are polynomials with
![]() $\mathrm{div} f=B$
and
$\mathrm{div} f=B$
and
![]() $\mathrm{div} g=\{p,q\}$
. Then
$\mathrm{div} g=\{p,q\}$
. Then
![]() $\sigma$
and
$\sigma$
and
![]() $\tau$
change the sign of
$\tau$
change the sign of
![]() $y$
and
$y$
and
![]() $z$
, respectively.
$z$
, respectively.
The involution
![]() $\sigma \tau$
is fixed-point free, so the quotient
$\sigma \tau$
is fixed-point free, so the quotient
![]() $\Gamma :=C_{\omega } /\langle{\sigma \tau } \rangle$
has genus 3; its field of functions is
$\Gamma :=C_{\omega } /\langle{\sigma \tau } \rangle$
has genus 3; its field of functions is
![]() $\mathbb{C}(x,w)$
, with
$\mathbb{C}(x,w)$
, with
![]() $w=yz$
and
$w=yz$
and
![]() $w^2=f(x)g(x)$
. We have again a cartesian square
$w^2=f(x)g(x)$
. We have again a cartesian square

Let
![]() $\alpha \in J\Gamma$
. We have
$\alpha \in J\Gamma$
. We have
![]() $\mathrm{Nm}_{\pi }\varphi ^*\alpha =\rho ^*\mathrm{Nm}_{\psi }\alpha =0$
; hence,
$\mathrm{Nm}_{\pi }\varphi ^*\alpha =\rho ^*\mathrm{Nm}_{\psi }\alpha =0$
; hence,
![]() $\varphi ^*$
maps
$\varphi ^*$
maps
![]() $J\Gamma$
into
$J\Gamma$
into
![]() $P\subset JC_{\omega }$
. Since
$P\subset JC_{\omega }$
. Since
![]() $\varphi$
is étale, we have
$\varphi$
is étale, we have
![]() $\mathrm{Ker} \varphi ^*=\mathbb{Z}/2$
; since
$\mathrm{Ker} \varphi ^*=\mathbb{Z}/2$
; since
![]() $\dim J\Gamma =\dim P=3$
,
$\dim J\Gamma =\dim P=3$
,
![]() $\varphi ^*$
is surjective.
$\varphi ^*$
is surjective.
3. Definition of
 $\Phi$
$\Phi$
Let
![]() $Y$
be a smooth degree
$Y$
be a smooth degree
![]() $d$
hypersurface in
$d$
hypersurface in
![]() $\mathbb{P}^N$
, defined by an equation
$\mathbb{P}^N$
, defined by an equation
![]() $f=0$
. Recall that one associates to
$f=0$
. Recall that one associates to
![]() $f$
a section
$f$
a section
![]() $h_f$
of
$h_f$
of
![]() $\mathsf{S}^2\Omega ^1_Y(d)$
, the hessian or second fundamental form of
$\mathsf{S}^2\Omega ^1_Y(d)$
, the hessian or second fundamental form of
![]() $f$
[Reference Griffiths and HarrisGH79]: at a point
$f$
[Reference Griffiths and HarrisGH79]: at a point
![]() $y$
of
$y$
of
![]() $Y$
, the intersection of
$Y$
, the intersection of
![]() $Y$
with the tangent hyperplane
$Y$
with the tangent hyperplane
![]() $H$
to
$H$
to
![]() $Y$
at
$Y$
at
![]() $y$
is a hypersurface in
$y$
is a hypersurface in
![]() $H$
singular at
$H$
singular at
![]() $y$
, and
$y$
, and
![]() $h_{f}(y)$
is the degree 2 term in the Taylor expansion of
$h_{f}(y)$
is the degree 2 term in the Taylor expansion of
![]() $f_{|H}$
at
$f_{|H}$
at
![]() $y$
.
$y$
.
Now let
![]() $X\subset \mathbb{P}^{n+r}$
be a smooth complete intersection of
$X\subset \mathbb{P}^{n+r}$
be a smooth complete intersection of
![]() $r$
hypersurfaces of degree
$r$
hypersurfaces of degree
![]() $d$
; let
$d$
; let
be the
![]() $r$
-dimensional subspace of degree
$r$
-dimensional subspace of degree
![]() $d$
polynomials vanishing on
$d$
polynomials vanishing on
![]() $X$
. By restricting
$X$
. By restricting
![]() $h_{f}$
, for
$h_{f}$
, for
![]() $f\in V$
, to
$f\in V$
, to
![]() $X$
, we get a linear map
$X$
, we get a linear map
which gives at each point
![]() $x\in X$
a linear space of quadratic forms on the tangent space
$x\in X$
a linear space of quadratic forms on the tangent space
![]() $T_{x}(X)$
. Note that when
$T_{x}(X)$
. Note that when
![]() $d=2$
, the corresponding quadrics in
$d=2$
, the corresponding quadrics in
![]() $\mathbb{P} (T_x(X))$
can be viewed geometrically as follows: The projective space
$\mathbb{P} (T_x(X))$
can be viewed geometrically as follows: The projective space
![]() $\mathbb{P}( T_x(X))$
can be identified with the space of lines in
$\mathbb{P}( T_x(X))$
can be identified with the space of lines in
![]() $\mathbb{P}^{n+r}$
passing through
$\mathbb{P}^{n+r}$
passing through
![]() $x$
and tangent to
$x$
and tangent to
![]() $X$
; then for each
$X$
; then for each
![]() $q\in V$
, the quadric defined by
$q\in V$
, the quadric defined by
![]() $h_q(x)$
parameterises the lines passing through
$h_q(x)$
parameterises the lines passing through
![]() $x$
and contained in the quadric
$x$
and contained in the quadric
![]() $\{q=0\}$
.
$\{q=0\}$
.
Now we want to consider the ‘inverse’ of the quadratic form
![]() $h_f(x)$
on
$h_f(x)$
on
![]() $T_x(X)$
; that is, the form on
$T_x(X)$
; that is, the form on
![]() $T^*_x(X)$
given in coordinates by the cofactor matrix. Intrinsically, each
$T^*_x(X)$
given in coordinates by the cofactor matrix. Intrinsically, each
![]() $f\in V$
gives a twisted symmetric morphism
$f\in V$
gives a twisted symmetric morphism
which induces a twisted symmetric morphism on
![]() $(n-1)$
-th exterior powers, namely,
$(n-1)$
-th exterior powers, namely,
We now observe that
![]() $K_X=\mathscr{O}_X(-n-1-r+dr)$
; hence
$K_X=\mathscr{O}_X(-n-1-r+dr)$
; hence
so
![]() $\wedge ^{n-1}h_f$
induces a symmetric morphism from
$\wedge ^{n-1}h_f$
induces a symmetric morphism from
![]() $\Omega ^1_X(n+1-r(d-1))$
to
$\Omega ^1_X(n+1-r(d-1))$
to
![]() $T_X((n-1)d-n-1+r(d-1))$
, hence provides a section
$T_X((n-1)d-n-1+r(d-1))$
, hence provides a section
Being locally given by the cofactor matrix,
![]() $\wedge ^{n-1}h_f$
is homogeneous of degree
$\wedge ^{n-1}h_f$
is homogeneous of degree
![]() $n-1$
in
$n-1$
in
![]() $f$
. Hence, we have constructed a linear map
$f$
. Hence, we have constructed a linear map
From now on, we restrict to the case
![]() $d=2,\,r=2$
, so
$d=2,\,r=2$
, so
![]() $X$
is the complete intersection of two quadrics, and the previous construction gives a linear map
$X$
is the complete intersection of two quadrics, and the previous construction gives a linear map
Using the canonical isomorphism
![]() $H^0(T^*X,\mathscr{O}_{T^*X})= H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X)$
, we deduce from
$H^0(T^*X,\mathscr{O}_{T^*X})= H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X)$
, we deduce from
![]() $\alpha$
a morphism
$\alpha$
a morphism
We have
![]() $\Phi (\lambda v)=\lambda ^2\Phi (v)$
for
$\Phi (\lambda v)=\lambda ^2\Phi (v)$
for
![]() $v\in T^*X$
,
$v\in T^*X$
,
![]() $\lambda \in \mathbb{C}$
, so
$\lambda \in \mathbb{C}$
, so
![]() $\Phi$
induces a rational map
$\Phi$
induces a rational map
whose indeterminacy locus
![]() $Z$
is the image of
$Z$
is the image of
![]() $\Phi ^{-1}(0)$
.
$\Phi ^{-1}(0)$
.
Proposition 3.1.
![]() $(1)\ \alpha$
is injective.
$(1)\ \alpha$
is injective.
![]() $(2)\ \Phi$
is surjective.
$(2)\ \Phi$
is surjective.
![]() $(3)$
The image of
$(3)$
The image of
![]() $Z$
by the structure map
$Z$
by the structure map
![]() $p:\mathbb{P} T^*X\rightarrow X$
is a proper subvariety of
$p:\mathbb{P} T^*X\rightarrow X$
is a proper subvariety of
![]() $X$
.
$X$
.
Proof. Let
![]() $x$
be a general point of
$x$
be a general point of
![]() $X$
. We claim that the base locus in
$X$
. We claim that the base locus in
![]() $\mathbb{P} (T_x(X))$
of the pencil of quadratic forms
$\mathbb{P} (T_x(X))$
of the pencil of quadratic forms
![]() $\{h_q(x)\}_{q\in V}$
is smooth. Indeed, this locus can be viewed as the variety
$\{h_q(x)\}_{q\in V}$
is smooth. Indeed, this locus can be viewed as the variety
![]() $F_x$
of lines in
$F_x$
of lines in
![]() $X$
passing through
$X$
passing through
![]() $x$
. Let
$x$
. Let
![]() $F$
be the Fano variety of lines contained in
$F$
be the Fano variety of lines contained in
![]() $X$
, and let
$X$
, and let
Then
![]() $F$
and therefore
$F$
and therefore
![]() $G$
are smooth [Reference ReidReid72, Theorem 2.6], hence
$G$
are smooth [Reference ReidReid72, Theorem 2.6], hence
![]() $F_x$
, which is the fibre above
$F_x$
, which is the fibre above
![]() $x$
of the projection
$x$
of the projection
![]() $G\rightarrow X$
, is smooth since
$G\rightarrow X$
, is smooth since
![]() $x$
is general. It follows that in an appropriate system of coordinates
$x$
is general. It follows that in an appropriate system of coordinates
![]() $(k_1,\ldots, k_n )$
of
$(k_1,\ldots, k_n )$
of
![]() $T_x(X)$
, the forms
$T_x(X)$
, the forms
![]() $\{h_q(x)\}$
can be written as
$\{h_q(x)\}$
can be written as
Then
![]() $\wedge ^{n-1}h_q(x)$
is given by the diagonal matrix with entries
$\wedge ^{n-1}h_q(x)$
is given by the diagonal matrix with entries
![]() $\beta _i:=\displaystyle \prod _{j\neq i}(t+\alpha _j)\ (i=1,\ldots, n)$
. These polynomials in
$\beta _i:=\displaystyle \prod _{j\neq i}(t+\alpha _j)\ (i=1,\ldots, n)$
. These polynomials in
![]() $t$
are linearly independent; hence, they generate the space of quadratic forms on
$t$
are linearly independent; hence, they generate the space of quadratic forms on
![]() $T^*_x(X)$
, which are diagonal in the basis
$T^*_x(X)$
, which are diagonal in the basis
![]() $(k_i)$
. This linear system has dimension
$(k_i)$
. This linear system has dimension
![]() $n$
, so
$n$
, so
![]() $\alpha$
is injective; it has no base point, so
$\alpha$
is injective; it has no base point, so
![]() $\varphi$
induces a finite, surjective morphism
$\varphi$
induces a finite, surjective morphism
![]() $\mathbb{P} (T^*_x(X))\rightarrow \mathbb{P}^{n-1}$
. Thus,
$\mathbb{P} (T^*_x(X))\rightarrow \mathbb{P}^{n-1}$
. Thus,
![]() $\Phi$
is surjective, and
$\Phi$
is surjective, and
![]() $Z\cap \mathbb{P} (T^*_x(X))=\varnothing$
, which gives (2) and (3).
$Z\cap \mathbb{P} (T^*_x(X))=\varnothing$
, which gives (2) and (3).
We want to give a geometric construction of the rational map
![]() $\varphi : \mathbb{P} T^*X\dashrightarrow \mathbb{P}^{n-1}$
. A point of
$\varphi : \mathbb{P} T^*X\dashrightarrow \mathbb{P}^{n-1}$
. A point of
![]() $\mathbb{P} T^*X$
is a pair
$\mathbb{P} T^*X$
is a pair
![]() $(x,H)$
, where
$(x,H)$
, where
![]() $x\in X$
and
$x\in X$
and
![]() $H$
is a hyperplane in
$H$
is a hyperplane in
![]() $T_x(X)$
. Restricting the pencil
$T_x(X)$
. Restricting the pencil
![]() $\{h_q(x)\}_{q\in V}$
to
$\{h_q(x)\}_{q\in V}$
to
![]() $H$
gives a pencil of quadrics on
$H$
gives a pencil of quadrics on
![]() $H$
, which for general
$H$
, which for general
![]() $(x,H)$
contains
$(x,H)$
contains
![]() $n-1$
singular quadrics
$n-1$
singular quadrics
![]() $q_1,\ldots, q_{n-1}$
. The subset
$q_1,\ldots, q_{n-1}$
. The subset
![]() $\{q_1,\ldots, q_{n-1}\}$
of
$\{q_1,\ldots, q_{n-1}\}$
of
![]() $\mathbb{P} (V)$
corresponds to a point
$\mathbb{P} (V)$
corresponds to a point
![]() $\varphi _{x,H}$
of
$\varphi _{x,H}$
of
![]() $\mathbb{P}(\mathsf{S}^{n-1}V^*)$
; namely, the hyperplane in
$\mathbb{P}(\mathsf{S}^{n-1}V^*)$
; namely, the hyperplane in
![]() $\mathsf{S}^{n-1}V$
spanned by
$\mathsf{S}^{n-1}V$
spanned by
![]() $q_1^{n-1},\ldots, q_{n-1}^{n-1}$
.
$q_1^{n-1},\ldots, q_{n-1}^{n-1}$
.
Proposition 3.2.
![]() $\varphi (x,H)=\varphi _{x,H}$
.
$\varphi (x,H)=\varphi _{x,H}$
.
Proof. We can assume that
![]() $x$
is general. We have seen that the restriction of
$x$
is general. We have seen that the restriction of
![]() $\varphi$
to
$\varphi$
to
![]() $\mathbb{P} (T^*_xX)$
is the morphism given by the linear system of quadratic forms
$\mathbb{P} (T^*_xX)$
is the morphism given by the linear system of quadratic forms
![]() $W\cong \mathsf{S}^{n-1}V$
spanned by the forms
$W\cong \mathsf{S}^{n-1}V$
spanned by the forms
![]() $\wedge ^{n-1}h_q(x)$
, for
$\wedge ^{n-1}h_q(x)$
, for
![]() $q\in V$
; in other words,
$q\in V$
; in other words,
![]() $\varphi$
maps the point
$\varphi$
maps the point
![]() $H$
of
$H$
of
![]() $\mathbb{P} (T^*_x(X))$
to the hyperplane of forms in
$\mathbb{P} (T^*_x(X))$
to the hyperplane of forms in
![]() $W$
vanishing at
$W$
vanishing at
![]() $H$
.
$H$
.
On the other hand,
![]() $\varphi _{x,H}$
is the hyperplane of
$\varphi _{x,H}$
is the hyperplane of
![]() $\mathsf{S}^{n-1}V$
spanned by the
$\mathsf{S}^{n-1}V$
spanned by the
![]() $q^{n-1}$
for those
$q^{n-1}$
for those
![]() $q\in V$
such that
$q\in V$
such that
![]() $h_q(x)_{|H}$
is singular; this condition is equivalent to saying that the form
$h_q(x)_{|H}$
is singular; this condition is equivalent to saying that the form
![]() $\wedge ^{n-1}h_q(x)$
on
$\wedge ^{n-1}h_q(x)$
on
![]() $T^*_xX$
vanishes at
$T^*_xX$
vanishes at
![]() $H$
. Therefore,
$H$
. Therefore,
![]() $\varphi _{x,H}$
is spanned by quadratic forms vanishing at
$\varphi _{x,H}$
is spanned by quadratic forms vanishing at
![]() $H$
, hence coincides with
$H$
, hence coincides with
![]() $\varphi (x,H)$
.
$\varphi (x,H)$
.
Corollary 3.3.
![]() $\mathrm{codim} Z\geq 2$
.
$\mathrm{codim} Z\geq 2$
.
Proof. Suppose that
![]() $Z$
contains a component
$Z$
contains a component
![]() $Z_0$
of codimension 1; since
$Z_0$
of codimension 1; since
![]() $p(Z)\neq X$
, we have
$p(Z)\neq X$
, we have
![]() $Z_0=p^{-1}(p(Z_0))$
. We claim that this is impossible; in fact,
$Z_0=p^{-1}(p(Z_0))$
. We claim that this is impossible; in fact,
![]() $Z$
cannot contain a fibre
$Z$
cannot contain a fibre
![]() $p^{-1}(x)$
. Indeed, its doing this would mean that for
$p^{-1}(x)$
. Indeed, its doing this would mean that for
![]() $q\in V$
, the form
$q\in V$
, the form
![]() $h_q(x)$
is singular along all hyperplanes
$h_q(x)$
is singular along all hyperplanes
![]() $H\subset T_x(X)$
; that is,
$H\subset T_x(X)$
; that is,
![]() $h_q(x)$
has rank
$h_q(x)$
has rank
![]() $\leq n-2$
. But the rank of
$\leq n-2$
. But the rank of
![]() $h_q(x)$
is the rank of the restriction of
$h_q(x)$
is the rank of the restriction of
![]() $q$
to the projective tangent subspace to
$q$
to the projective tangent subspace to
![]() $X$
at
$X$
at
![]() $x$
. Restricting a quadratic form to a hyperplane lowers its rank by up to two. Since a general
$x$
. Restricting a quadratic form to a hyperplane lowers its rank by up to two. Since a general
![]() $q$
in
$q$
in
![]() $V$
has rank
$V$
has rank
![]() $n+3$
, its restriction to a codimension 2 subspace has rank
$n+3$
, its restriction to a codimension 2 subspace has rank
![]() $\geq n-1$
.
$\geq n-1$
.
4. Fibers of
 $\boldsymbol\varphi$
$\boldsymbol\varphi$
In an appropriate system of coordinates
![]() $(x_0,\ldots, x_{n+2})$
, our variety
$(x_0,\ldots, x_{n+2})$
, our variety
![]() $X$
is defined by the equations
$X$
is defined by the equations
![]() $q_1=q_2=0$
, with
$q_1=q_2=0$
, with
Let
![]() $\Pi =\mathbb{P}(V)\ (\cong \mathbb{P}^1)$
be the pencil of quadrics containing
$\Pi =\mathbb{P}(V)\ (\cong \mathbb{P}^1)$
be the pencil of quadrics containing
![]() $X$
. We choose a coordinate
$X$
. We choose a coordinate
![]() $t$
on
$t$
on
![]() $\Pi$
so that the quadrics of
$\Pi$
so that the quadrics of
![]() $\Pi$
are given by
$\Pi$
are given by
![]() $tq_1-q_2=0$
. Then the singular quadrics of
$tq_1-q_2=0$
. Then the singular quadrics of
![]() $\Pi$
correspond to the points
$\Pi$
correspond to the points
![]() $\mu _0,\ldots, \mu _{n+2}$
.
$\mu _0,\ldots, \mu _{n+2}$
.
The goal of this section is to describe the general fibre of the rational map
![]() $\varphi :\mathbb{P} T^*X\dashrightarrow \mathsf{S}^{n-1}\Pi$
$\varphi :\mathbb{P} T^*X\dashrightarrow \mathsf{S}^{n-1}\Pi$
![]() $(\cong \mathbb{P}^{n-1})$
. For
$(\cong \mathbb{P}^{n-1})$
. For
![]() $\lambda =(\lambda _1,\ldots, \lambda _{n-1})\in \mathsf{S}^{n-1}\Pi$
, let
$\lambda =(\lambda _1,\ldots, \lambda _{n-1})\in \mathsf{S}^{n-1}\Pi$
, let
![]() $C_{\mu, \lambda }$
denote the hyperelliptic curve
$C_{\mu, \lambda }$
denote the hyperelliptic curve
![]() $y^2= \prod (t-\mu _i)\prod (t-\lambda _j)$
, of genus
$y^2= \prod (t-\mu _i)\prod (t-\lambda _j)$
, of genus
![]() $n$
. We will then prove the following:
$n$
. We will then prove the following:
Proposition 4.1.
For
![]() $\lambda$
general in
$\lambda$
general in
![]() $\mathsf{S}^{n-1}\Pi$
, the fibre
$\mathsf{S}^{n-1}\Pi$
, the fibre
![]() $\varphi ^{-1}(\lambda )$
is birational to the quotient of the Jacobian
$\varphi ^{-1}(\lambda )$
is birational to the quotient of the Jacobian
![]() $JC_{\mu, \lambda }$
by the group
$JC_{\mu, \lambda }$
by the group
![]() $\Gamma :=\{\pm 1_{JC}\}\times \Gamma ^+$
, where
$\Gamma :=\{\pm 1_{JC}\}\times \Gamma ^+$
, where
![]() $\Gamma ^+\cong (\mathbb{Z}/2Z)^{n-2}$
is a group of translations by
$\Gamma ^+\cong (\mathbb{Z}/2Z)^{n-2}$
is a group of translations by
![]() $2$
-torsion elements.
$2$
-torsion elements.
4.1 Odd-dimensional intersection of 2 quadrics
We briefly recall here the results of Reid’s thesis ([Reference ReidReid72]; see also [Reference Desale and RamananDR76]). Let
![]() $Y\subset \mathbb{P}^{2g+1}$
be a smooth intersection of 2 quadrics, and let
$Y\subset \mathbb{P}^{2g+1}$
be a smooth intersection of 2 quadrics, and let
![]() $\Xi \ (\cong \mathbb{P}^1)$
be the pencil of quadrics containing
$\Xi \ (\cong \mathbb{P}^1)$
be the pencil of quadrics containing
![]() $Y$
. Let
$Y$
. Let
![]() $\Sigma \subset \Xi$
be the subset of
$\Sigma \subset \Xi$
be the subset of
![]() $2g+2$
points corresponding to singular quadrics, and let
$2g+2$
points corresponding to singular quadrics, and let
![]() $C$
be the double covering of
$C$
be the double covering of
![]() $\Xi$
branched along
$\Xi$
branched along
![]() $\Sigma$
; this is a hyperelliptic curve of genus
$\Sigma$
; this is a hyperelliptic curve of genus
![]() $g$
. The intermediate Jacobian
$g$
. The intermediate Jacobian
![]() $JY$
of
$JY$
of
![]() $Y$
is isomorphic to
$Y$
is isomorphic to
![]() $JC$
(as principally polarized abelian varieties). The variety
$JC$
(as principally polarized abelian varieties). The variety
![]() $F$
of
$F$
of
![]() $(g-1)$
-planes contained in
$(g-1)$
-planes contained in
![]() $Y$
is also isomorphic to
$Y$
is also isomorphic to
![]() $JC$
, but this isomorphism is not canonical.
$JC$
, but this isomorphism is not canonical.
In an appropriate system of coordinates, the equations of
![]() $Y$
are of the form
$Y$
are of the form
then
![]() $\Sigma =\{\alpha _1,\ldots, \alpha _{2g+2}\}$
. The group
$\Sigma =\{\alpha _1,\ldots, \alpha _{2g+2}\}$
. The group
![]() $\Gamma :=(\mathbb{Z}/2\mathbb{Z})^{2g+1}$
acts on
$\Gamma :=(\mathbb{Z}/2\mathbb{Z})^{2g+1}$
acts on
![]() $Y$
(hence also on
$Y$
(hence also on
![]() $F$
) by changing the signs of the coordinates. Let
$F$
) by changing the signs of the coordinates. Let
![]() $\Gamma ^+\subset \Gamma$
be the subgroup of elements that change an even number of coordinates. Choose an element
$\Gamma ^+\subset \Gamma$
be the subgroup of elements that change an even number of coordinates. Choose an element
![]() $\gamma \in \Gamma \smallsetminus \Gamma ^+$
; there is an isomorphism
$\gamma \in \Gamma \smallsetminus \Gamma ^+$
; there is an isomorphism
![]() $F\stackrel{\sim }{\longrightarrow } JC$
such that
$F\stackrel{\sim }{\longrightarrow } JC$
such that
![]() $\gamma$
corresponds to (-1JC). Then the image of
$\gamma$
corresponds to (-1JC). Then the image of
![]() $\Gamma ^+$
in
$\Gamma ^+$
in
![]() $\mathrm{Aut}(JC)$
is the group
$\mathrm{Aut}(JC)$
is the group
![]() $T_2$
of translations by
$T_2$
of translations by
![]() $2$
-torsion elements of
$2$
-torsion elements of
![]() $JC$
, and the image of
$JC$
, and the image of
![]() $\Gamma$
is
$\Gamma$
is
![]() $T_2\times \{\pm 1_{JC}\}$
[Reference Desale and RamananDR76, Lemma 4.5].
$T_2\times \{\pm 1_{JC}\}$
[Reference Desale and RamananDR76, Lemma 4.5].
4.2 An auxiliary construction
We consider the projective space
![]() $\mathbb{P}^{2n+1}$
equipped with the system of homogeneous coordinates
$\mathbb{P}^{2n+1}$
equipped with the system of homogeneous coordinates
and the affine space
![]() $\mathbb{A}^{n-1}$
equipped with the affine coordinates
$\mathbb{A}^{n-1}$
equipped with the affine coordinates
![]() $\lambda _1,\ldots, \lambda _{n-1}$
. Let
$\lambda _1,\ldots, \lambda _{n-1}$
. Let
be the complete intersection of the two quadrics with equations
 \begin{equation*}Q_1=Q_2=0\quad \mbox {with}\quad Q_1=\sum _{i=0}^{n+2}x_i^2+\sum _{j=1}^{n-1}y_j^2\quad, \quad Q_2=\sum _{i=0}^{n+2}\mu _ix_i^2+\sum _{j=1}^{n-1}\lambda _jy_j^2\, .\end{equation*}
\begin{equation*}Q_1=Q_2=0\quad \mbox {with}\quad Q_1=\sum _{i=0}^{n+2}x_i^2+\sum _{j=1}^{n-1}y_j^2\quad, \quad Q_2=\sum _{i=0}^{n+2}\mu _ix_i^2+\sum _{j=1}^{n-1}\lambda _jy_j^2\, .\end{equation*}
The second projection,
![]() $\mathscr{X}\rightarrow \mathbb{A}^{n-1},$
gives a family of complete intersections of two quadrics
$\mathscr{X}\rightarrow \mathbb{A}^{n-1},$
gives a family of complete intersections of two quadrics
![]() $\mathscr{X}_\lambda$
of dimension
$\mathscr{X}_\lambda$
of dimension
![]() $2n-1$
parameterised by
$2n-1$
parameterised by
![]() $ \mathbb{A}^{n-1}$
. Note that
$ \mathbb{A}^{n-1}$
. Note that
![]() $X$
is the intersection of
$X$
is the intersection of
![]() $\mathscr{X}$
with the subspace
$\mathscr{X}$
with the subspace
![]() $\mathbb{P}^{n+2}\subset \mathbb{P}^{2n+1}$
defined by
$\mathbb{P}^{n+2}\subset \mathbb{P}^{2n+1}$
defined by
![]() $y_1=\ldots =y_{n-1}=0$
.
$y_1=\ldots =y_{n-1}=0$
.
Let
![]() $p: \mathscr{F}\rightarrow \mathbb{A}^{n-1}$
be the family of
$p: \mathscr{F}\rightarrow \mathbb{A}^{n-1}$
be the family of
![]() $(n-1)$
-planes contained in the
$(n-1)$
-planes contained in the
![]() $\mathscr{X}_{\lambda }$
; that is
$\mathscr{X}_{\lambda }$
; that is
For
![]() $\lambda$
general, the fibre
$\lambda$
general, the fibre
![]() $\mathscr{F}_{\lambda }$
is isomorphic to the Jacobian of the hyperelliptic curve
$\mathscr{F}_{\lambda }$
is isomorphic to the Jacobian of the hyperelliptic curve
![]() $C_{\mu, \lambda }$
(4.1).
$C_{\mu, \lambda }$
(4.1).
Let
![]() $(P,\lambda )$
be a general point of
$(P,\lambda )$
be a general point of
![]() $\mathscr{F}$
. Then
$\mathscr{F}$
. Then
![]() $P\,\cap \, \mathbb{P}^{n+2}$
is a point
$P\,\cap \, \mathbb{P}^{n+2}$
is a point
![]() $x$
of
$x$
of
![]() $X$
. Let
$X$
. Let
![]() $\pi :\mathbb{P}^{2n+1}\dashrightarrow \mathbb{P}^{n+2}$
be the projection
$\pi :\mathbb{P}^{2n+1}\dashrightarrow \mathbb{P}^{n+2}$
be the projection
![]() $(x_i,y_j)\mapsto (x_i)$
. Since the
$(x_i,y_j)\mapsto (x_i)$
. Since the
![]() $\pi_*$
differentials of
$\pi_*$
differentials of
![]() $Q_i$
and
$Q_i$
and
![]() $q_i$
coincide at
$q_i$
coincide at
![]() $x$
, the differential
$x$
, the differential
![]() $\pi$
* maps
$\pi$
* maps
![]() $T_x(P)\subset T_x(\mathscr{X})$
into
$T_x(P)\subset T_x(\mathscr{X})$
into
![]() $T_x(X)$
. Since
$T_x(X)$
. Since
![]() $P$
is general,
$P$
is general,
![]() $\pi _*T_x(P)$
is a hyperplane in
$\pi _*T_x(P)$
is a hyperplane in
![]() $T_x(X)$
; this will follow from the proof of Proposition 4.2, (1) below, where we explicitly construct pairs
$T_x(X)$
; this will follow from the proof of Proposition 4.2, (1) below, where we explicitly construct pairs
![]() $(P,\lambda )$
with this property.
$(P,\lambda )$
with this property.
Therefore, we have a rational map
The symmetric group
![]() $\mathfrak{S}_{n-1}$
acts on
$\mathfrak{S}_{n-1}$
acts on
![]() $\mathbb{P}^{2n+1}$
by permuting the
$\mathbb{P}^{2n+1}$
by permuting the
![]() $y_j$
and acts on the group
$y_j$
and acts on the group
![]() $(\mathbb{Z}/2\mathbb{Z})^{n-1}$
by changing their signs; this gives an action of the semi-direct product
$(\mathbb{Z}/2\mathbb{Z})^{n-1}$
by changing their signs; this gives an action of the semi-direct product
![]() $G:=(\mathbb{Z}/2\mathbb{Z})^{n-1}\rtimes \mathfrak{S}_{n-1}$
. We make
$G:=(\mathbb{Z}/2\mathbb{Z})^{n-1}\rtimes \mathfrak{S}_{n-1}$
. We make
![]() $G$
act on
$G$
act on
![]() $\mathbb{A}^{n-1}$
through its quotient
$\mathbb{A}^{n-1}$
through its quotient
![]() $\mathfrak{S}_{n-1}$
, by permutation of the
$\mathfrak{S}_{n-1}$
, by permutation of the
![]() $\lambda _i$
. This induces an action of
$\lambda _i$
. This induces an action of
![]() $G$
on
$G$
on
![]() $\mathscr{X}$
and therefore on
$\mathscr{X}$
and therefore on
![]() $\mathscr{F}$
, which is compatible via
$\mathscr{F}$
, which is compatible via
![]() $p$
with the action on the base. The map
$p$
with the action on the base. The map
![]() $\psi$
is invariant under this action; hence, it factors through the quotient
$\psi$
is invariant under this action; hence, it factors through the quotient
![]() $\mathscr{F}/G$
. By passing to the quotient, we get a map
$\mathscr{F}/G$
. By passing to the quotient, we get a map
![]() $p^\sharp : \mathscr{F}/G\rightarrow \mathbb{A}^{n-1} /\mathfrak{S}_{n-1}$
.
$p^\sharp : \mathscr{F}/G\rightarrow \mathbb{A}^{n-1} /\mathfrak{S}_{n-1}$
.
Proposition 4.2.
![]() $(1)\ \psi$
induces a birational map
$(1)\ \psi$
induces a birational map
![]() $\psi ^{\sharp }:\mathscr{F}/G\dashrightarrow \mathbb{P} T^*X$
.
$\psi ^{\sharp }:\mathscr{F}/G\dashrightarrow \mathbb{P} T^*X$
.
![]() $(2)$
There is a commutative diagram
$(2)$
There is a commutative diagram

where
![]() $p^{\sharp }$
is deduced from
$p^{\sharp }$
is deduced from
![]() $p$
and where
$p$
and where
![]() $\sigma$
is the isomorphism given by symmetric functions.
$\sigma$
is the isomorphism given by symmetric functions.
Proof. (1) Let
![]() $(x,H)\in \mathbb{P} T^*X$
; we want to describe the pairs
$(x,H)\in \mathbb{P} T^*X$
; we want to describe the pairs
![]() $(P,\lambda )$
such that
$(P,\lambda )$
such that
![]() $P\cap \mathbb{P}^{n+2}=\{x\}$
and
$P\cap \mathbb{P}^{n+2}=\{x\}$
and
![]() $\pi _*T_x(P)=H$
. The latter condition says that via the decomposition
$\pi _*T_x(P)=H$
. The latter condition says that via the decomposition
![]() $T_x(P)$
identifies with the graph of a linear map
$T_x(P)$
identifies with the graph of a linear map
Using the basis
![]() $(\frac{\partial }{\partial y_1},\ldots, \frac{\partial }{\partial y_{n-1}} )$
of
$(\frac{\partial }{\partial y_1},\ldots, \frac{\partial }{\partial y_{n-1}} )$
of
![]() $\mathrm{Ker}\, \pi _*$
, we have
$\mathrm{Ker}\, \pi _*$
, we have
![]() $\alpha =(\alpha _1,\ldots, \alpha _{n-1})$
, where the
$\alpha =(\alpha _1,\ldots, \alpha _{n-1})$
, where the
![]() $\alpha _i$
are linear forms on
$\alpha _i$
are linear forms on
![]() $H$
. The condition
$H$
. The condition
![]() $P\subset \mathscr{X}_{\lambda }$
implies that the hessians
$P\subset \mathscr{X}_{\lambda }$
implies that the hessians
![]() $h_{Q_1}(x)$
and
$h_{Q_1}(x)$
and
![]() $h_{Q_2}(x)$
vanish on
$h_{Q_2}(x)$
vanish on
![]() $T_x(P)$
, which gives
$T_x(P)$
, which gives
This is a simultaneous diagonalisation of the quadratic forms
![]() $h_{q_1}(x)_{\mid H}$
and
$h_{q_1}(x)_{\mid H}$
and
![]() $h_{q_2}(x)_{\mid H}$
; when they are in general position, this determines the
$h_{q_2}(x)_{\mid H}$
; when they are in general position, this determines the
![]() $\lambda _i$
up to permutation and the
$\lambda _i$
up to permutation and the
![]() $\alpha _i$
up to sign and permutation, which proves (1).
$\alpha _i$
up to sign and permutation, which proves (1).
(2) Let
![]() $(P,\lambda )\in \mathscr{F}$
, and let
$(P,\lambda )\in \mathscr{F}$
, and let
![]() $(x,H):=\psi (P,\lambda )$
. According to Proposition 3.2,
$(x,H):=\psi (P,\lambda )$
. According to Proposition 3.2,
![]() $\varphi (x,H)$
is given by the
$\varphi (x,H)$
is given by the
![]() $(n-1)$
-uple of quadrics
$(n-1)$
-uple of quadrics
![]() $ q\in \Pi$
such that the form
$ q\in \Pi$
such that the form
![]() $h_{q}(x)_{\mid H}$
is singular. Using
$h_{q}(x)_{\mid H}$
is singular. Using
![]() $(\alpha _1,\ldots, \alpha _{n-1})$
as coordinates on
$(\alpha _1,\ldots, \alpha _{n-1})$
as coordinates on
![]() $H$
, we see from (1) that this
$H$
, we see from (1) that this
![]() $(n-1)$
-uple is given by
$(n-1)$
-uple is given by
![]() $(\lambda _1,\ldots, \lambda _{n-1})$
, which proves (2).
$(\lambda _1,\ldots, \lambda _{n-1})$
, which proves (2).
4.3 Proof of Proposition 4.1.
Let
![]() $\lambda$
be a general element of
$\lambda$
be a general element of
![]() $\mathbb{A}^{n-1}$
. Let us denote by
$\mathbb{A}^{n-1}$
. Let us denote by
![]() $\Gamma$
the subgroup
$\Gamma$
the subgroup
![]() $(\mathbb{Z}/2\mathbb{Z})^{n-1}$
of
$(\mathbb{Z}/2\mathbb{Z})^{n-1}$
of
![]() $G$
. From Proposition 4.2 and the cartesian diagram
$G$
. From Proposition 4.2 and the cartesian diagram

we see that the fibre
![]() $\varphi ^{-1}(\lambda )$
is birational to the quotient
$\varphi ^{-1}(\lambda )$
is birational to the quotient
![]() $\mathscr{F}_{\lambda }/\Gamma$
. By (4.1) there is an isomorphism
$\mathscr{F}_{\lambda }/\Gamma$
. By (4.1) there is an isomorphism
![]() $\mathscr{F}_{\lambda } \stackrel{\sim }{\longrightarrow } JC_{\mu, \lambda }$
such that
$\mathscr{F}_{\lambda } \stackrel{\sim }{\longrightarrow } JC_{\mu, \lambda }$
such that
![]() $\Gamma$
acts on
$\Gamma$
acts on
![]() $JC_{\mu, \lambda }$
as
$JC_{\mu, \lambda }$
as
![]() $\{\pm 1_{J}\} \times \Gamma ^+$
, where
$\{\pm 1_{J}\} \times \Gamma ^+$
, where
![]() $\Gamma ^+$
is a group of translations by
$\Gamma ^+$
is a group of translations by
![]() $2$
-torsion elements. This proves the proposition.
$2$
-torsion elements. This proves the proposition.
5. Fibres of
 $\Phi$
$\Phi$
5.1 Results
We keep the settings of the previous section. Recall that our parameter
![]() $\lambda$
lives in
$\lambda$
lives in
![]() $\mathbb{A}^{n-1}\subset \mathsf{S}^{n-1}\Pi \cong \mathbb{P}^{n-1}$
. For
$\mathbb{A}^{n-1}\subset \mathsf{S}^{n-1}\Pi \cong \mathbb{P}^{n-1}$
. For
![]() $\lambda$
in
$\lambda$
in
![]() $\mathbb{A}^{n-1}$
, we denote by
$\mathbb{A}^{n-1}$
, we denote by
![]() $\tilde{\lambda }$
a lift of
$\tilde{\lambda }$
a lift of
![]() $\lambda$
in
$\lambda$
in
![]() $\mathbb{C}^n$
for the quotient map
$\mathbb{C}^n$
for the quotient map
![]() $\mathbb{C}^n\smallsetminus \{0\}\rightarrow \mathbb{P}^{n-1}$
.
$\mathbb{C}^n\smallsetminus \{0\}\rightarrow \mathbb{P}^{n-1}$
.
Theorem 5.1.
Assume that
![]() $X$
is general. For
$X$
is general. For
![]() $\lambda \in \mathbb{A}^{n-1}$
general, the fibre
$\lambda \in \mathbb{A}^{n-1}$
general, the fibre
![]() $\Phi ^{-1}(\tilde{\lambda } )$
is isomorphic to
$\Phi ^{-1}(\tilde{\lambda } )$
is isomorphic to
![]() $A\smallsetminus Z$
, where:
$A\smallsetminus Z$
, where:
![]() $\bullet \ A$
is the abelian variety quotient of
$\bullet \ A$
is the abelian variety quotient of
![]() $JC_{\mu, \lambda }$
by a
$JC_{\mu, \lambda }$
by a
![]() $2$
-torsion subgroup, isomorphic to
$2$
-torsion subgroup, isomorphic to
![]() $(\mathbb{Z}/2\mathbb{Z})^{n-2}\,$
;
$(\mathbb{Z}/2\mathbb{Z})^{n-2}\,$
;
![]() $\bullet \ Z$
is a closed subvariety of codimension
$\bullet \ Z$
is a closed subvariety of codimension
![]() $\geq 2$
in
$\geq 2$
in
![]() $A$
.
$A$
.
Corollary 5.2.
For every smooth complete intersection of two quadrics
![]() $X\subset \mathbb{P}^{n+2}$
, the fibration
$X\subset \mathbb{P}^{n+2}$
, the fibration
![]() $\Phi :T^*X\rightarrow \mathbb{C}^n$
is Lagrangian.
$\Phi :T^*X\rightarrow \mathbb{C}^n$
is Lagrangian.
Proof. Assume first that
![]() $X$
is general. The symplectic form on
$X$
is general. The symplectic form on
![]() $T^*X$
is
$T^*X$
is
![]() $d\eta$
, where
$d\eta$
, where
![]() $\eta$
is the Liouville form. By Theorem 5.1 and Hartogs’ principle, the pull-back of
$\eta$
is the Liouville form. By Theorem 5.1 and Hartogs’ principle, the pull-back of
![]() $\eta$
to a general fibre of
$\eta$
to a general fibre of
![]() $\Phi$
is the restriction of a 1-form on an abelian variety, hence is closed. This implies the result.
$\Phi$
is the restriction of a 1-form on an abelian variety, hence is closed. This implies the result.
Let
![]() $p:\mathscr{X}\rightarrow B$
be a complete family of smooth intersection of two quadrics in
$p:\mathscr{X}\rightarrow B$
be a complete family of smooth intersection of two quadrics in
![]() $\mathbb{P}^{n+2}$
. The constructions of §3 can be globalised over
$\mathbb{P}^{n+2}$
. The constructions of §3 can be globalised over
![]() $B$
: we have a rank 2 vector bundle
$B$
: we have a rank 2 vector bundle
![]() $\mathscr{V}$
over
$\mathscr{V}$
over
![]() $B$
whose fibre at a point
$B$
whose fibre at a point
![]() $b\in B$
is the space of quadratic forms vanishing on
$b\in B$
is the space of quadratic forms vanishing on
![]() $\mathscr{X}_b$
. We get a homomorphism
$\mathscr{X}_b$
. We get a homomorphism
![]() $\mathsf{S}^{n-1}\mathscr{V}\rightarrow p_*T_{\mathscr{X}/B}$
, which thus gives rise to a morphism
$\mathsf{S}^{n-1}\mathscr{V}\rightarrow p_*T_{\mathscr{X}/B}$
, which thus gives rise to a morphism
![]() $\boldsymbol{\Phi }:T^*(\mathscr{X}/B)\rightarrow \mathsf{S}^{n-1}\mathscr{V}^*$
over
$\boldsymbol{\Phi }:T^*(\mathscr{X}/B)\rightarrow \mathsf{S}^{n-1}\mathscr{V}^*$
over
![]() $B$
which induces over each point
$B$
which induces over each point
![]() $b\in B$
our map
$b\in B$
our map
![]() $\Phi$
. There is a natural Liouville form
$\Phi$
. There is a natural Liouville form
![]() $\boldsymbol{\eta }$
on
$\boldsymbol{\eta }$
on
![]() $T^*(\mathscr{X}/B)$
: Since
$T^*(\mathscr{X}/B)$
: Since
![]() $d\boldsymbol{\eta }$
vanishes on a general fibre of
$d\boldsymbol{\eta }$
vanishes on a general fibre of
![]() $\boldsymbol{\Phi }$
, it vanishes on all fibres.
$\boldsymbol{\Phi }$
, it vanishes on all fibres.
Corollary 5.3.
Assume that
![]() $X$
is general. The multiplication map
$X$
is general. The multiplication map
![]() $\mathsf{S}^{\scriptscriptstyle \bullet } H^0(X,\mathsf{S}^2T_X)\rightarrow H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X)$
is an isomorphism.
$\mathsf{S}^{\scriptscriptstyle \bullet } H^0(X,\mathsf{S}^2T_X)\rightarrow H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X)$
is an isomorphism.
(We will give in Section 7 a proof that is valid with no generality assumption.)
Proof. Theorem 5.1 implies that every function on a general fibre of
![]() $\Phi$
is constant; hence, the pull-back
$\Phi$
is constant; hence, the pull-back
![]() $\Phi ^*:H^0(\mathbb{C}^n,\mathscr{O}_{\mathbb{C}^n})\rightarrow H^0(T^*X,\mathscr{O}_{T^*X})$
is an isomorphism. The right-hand space is canonically isomorphic to
$\Phi ^*:H^0(\mathbb{C}^n,\mathscr{O}_{\mathbb{C}^n})\rightarrow H^0(T^*X,\mathscr{O}_{T^*X})$
is an isomorphism. The right-hand space is canonically isomorphic to
![]() $H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X)$
; hence, we get an algebra isomorphism
$H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X)$
; hence, we get an algebra isomorphism
![]() $\mathbb{C}[t_1,\ldots, t_n]\stackrel{\sim }{\longrightarrow } H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X)$
. By construction, the
$\mathbb{C}[t_1,\ldots, t_n]\stackrel{\sim }{\longrightarrow } H^0(X,\mathsf{S}^{\scriptscriptstyle \bullet }T_X)$
. By construction, the
![]() $t_i$
are mapped to elements of
$t_i$
are mapped to elements of
![]() $H^0(X,\mathsf{S}^{2}T_X)$
, so the Corollary follows.
$H^0(X,\mathsf{S}^{2}T_X)$
, so the Corollary follows.
Remark 5.4. Let
![]() $V_1,\ldots, V_n$
be the Hamiltonian vector fields on
$V_1,\ldots, V_n$
be the Hamiltonian vector fields on
![]() $T^*X$
that are associated to the components of
$T^*X$
that are associated to the components of
![]() $\Phi$
. For
$\Phi$
. For
![]() $\lambda$
general in
$\lambda$
general in
![]() $\mathbb{C}^n$
, let us identify
$\mathbb{C}^n$
, let us identify
![]() $\Phi ^{-1}(\lambda )$
to
$\Phi ^{-1}(\lambda )$
to
![]() $A\smallsetminus Z$
as in the theorem. Then by Hartogs’ principle the
$A\smallsetminus Z$
as in the theorem. Then by Hartogs’ principle the
![]() $V_i$
linearise on
$V_i$
linearise on
![]() $A$
; that is, they extend to a basis of
$A$
; that is, they extend to a basis of
![]() $H^0(A,T_A)$
. In principle, this allows to write explicit solutions of the Hamilton equations for
$H^0(A,T_A)$
. In principle, this allows to write explicit solutions of the Hamilton equations for
![]() $\Phi _i$
in terms of theta functions.
$\Phi _i$
in terms of theta functions.
5.2 Proof of the theorem: lemmas
We fix a general point
![]() $\lambda \in \mathbb{A}^{n-1}$
. We denote by
$\lambda \in \mathbb{A}^{n-1}$
. We denote by
![]() $\mathscr{F}^{\mathrm{o}}$
the open subset of
$\mathscr{F}^{\mathrm{o}}$
the open subset of
![]() $\mathscr{F}$
where the rational map
$\mathscr{F}$
where the rational map
![]() $\psi$
is well-defined and denote by
$\psi$
is well-defined and denote by
![]() $\mathscr{F}^{\mathrm{o}}_{\lambda }$
its intersection with the fibre
$\mathscr{F}^{\mathrm{o}}_{\lambda }$
its intersection with the fibre
![]() $\mathscr{F}_{\lambda }$
. Since
$\mathscr{F}_{\lambda }$
. Since
![]() $\lambda$
is general, the complement of
$\lambda$
is general, the complement of
![]() $\mathscr{F}^{\mathrm{o}}_{\lambda }$
in
$\mathscr{F}^{\mathrm{o}}_{\lambda }$
in
![]() $\mathscr{F}_{\lambda }$
has codimension
$\mathscr{F}_{\lambda }$
has codimension
![]() $\geq 2$
. The rational map
$\geq 2$
. The rational map
![]() $\psi$
induces a morphism
$\psi$
induces a morphism
![]() $\psi ^{\mathrm{o}}: \mathscr{F}^{\mathrm{o}}\rightarrow \mathbb{P} T^*X$
; we denote by
$\psi ^{\mathrm{o}}: \mathscr{F}^{\mathrm{o}}\rightarrow \mathbb{P} T^*X$
; we denote by
![]() $\psi ^{\mathrm{o}}_{\lambda }$
its restriction to
$\psi ^{\mathrm{o}}_{\lambda }$
its restriction to
![]() $\mathscr{F}_{\lambda }^{\mathrm{o}}$
. Let
$\mathscr{F}_{\lambda }^{\mathrm{o}}$
. Let
![]() $Z\subset \mathbb{P} T^*X$
be the indeterminacy locus of
$Z\subset \mathbb{P} T^*X$
be the indeterminacy locus of
![]() $\varphi$
(§ 3), and let
$\varphi$
(§ 3), and let
![]() $\mathscr{F}_{\lambda }^{\mathrm{bad} }:= (\psi ^{\mathrm{o}}_{\lambda })^{-1}(Z)\subset \mathscr{F}^{\mathrm{o}}_{\lambda }$
.
$\mathscr{F}_{\lambda }^{\mathrm{bad} }:= (\psi ^{\mathrm{o}}_{\lambda })^{-1}(Z)\subset \mathscr{F}^{\mathrm{o}}_{\lambda }$
.
Proposition 5.5.
![]() $\mathscr{F}_{\lambda }^{\mathrm{bad} }$
has codimension
$\mathscr{F}_{\lambda }^{\mathrm{bad} }$
has codimension
![]() $\geq 2$
in
$\geq 2$
in
![]() $\mathscr{F}_{\lambda }$
.
$\mathscr{F}_{\lambda }$
.
We postpone the proof of Proposition 5.5 to the next section; here we show how it implies Theorem 5.1.
Let
![]() $0_X\subset T^*X$
be the zero section, and let
$0_X\subset T^*X$
be the zero section, and let
![]() $q:T^*X\smallsetminus 0_X\rightarrow \mathbb{P} T^*X$
be the quotient map. Let
$q:T^*X\smallsetminus 0_X\rightarrow \mathbb{P} T^*X$
be the quotient map. Let
![]() $\varphi ^{\mathrm{o}}: \mathbb{P} T^*X\smallsetminus Z\rightarrow \mathbb{P}^{n-1}$
be the morphism induced by
$\varphi ^{\mathrm{o}}: \mathbb{P} T^*X\smallsetminus Z\rightarrow \mathbb{P}^{n-1}$
be the morphism induced by
![]() $\varphi$
. We thus have
$\varphi$
. We thus have
![]() $\ q(\Phi ^{-1}(\tilde{\lambda } ))= (\varphi ^{\mathrm{o}})^{-1}(\lambda )$
, and the restriction
$\ q(\Phi ^{-1}(\tilde{\lambda } ))= (\varphi ^{\mathrm{o}})^{-1}(\lambda )$
, and the restriction
is an étale double cover, with Galois involution
![]() $\iota$
induced by
$\iota$
induced by
![]() $(-1_{T^*X})$
.
$(-1_{T^*X})$
.
We put
![]() $\mathscr{F}_{\lambda }^{\mathrm{oo}}:= \mathscr{F}_{\lambda }^{\mathrm{o}}\smallsetminus \mathscr{F}_{\lambda }^{\mathrm{bad} }$
and consider the restriction
$\mathscr{F}_{\lambda }^{\mathrm{oo}}:= \mathscr{F}_{\lambda }^{\mathrm{o}}\smallsetminus \mathscr{F}_{\lambda }^{\mathrm{bad} }$
and consider the restriction
Lemma 5.6.
The fibre
![]() $\Phi ^{-1}(\tilde{\lambda })$
is Lagrangian, and has a trivial tangent bundle.
$\Phi ^{-1}(\tilde{\lambda })$
is Lagrangian, and has a trivial tangent bundle.
Proof. The étale double cover
![]() $q_{\lambda }$
induces by fibred product an étale double cover
$q_{\lambda }$
induces by fibred product an étale double cover
such that
![]() $\psi ^{\mathrm{o}}_{\lambda }$
lifts to a morphism
$\psi ^{\mathrm{o}}_{\lambda }$
lifts to a morphism
![]() $\tilde{\psi }^{\mathrm{o}}_{\lambda }: \widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}\rightarrow \Phi ^{-1}(\tilde{\lambda } )$
.
$\tilde{\psi }^{\mathrm{o}}_{\lambda }: \widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}\rightarrow \Phi ^{-1}(\tilde{\lambda } )$
.
By Proposition 5.5, the complement of
![]() $\mathscr{F}_{\lambda }^{\mathrm{oo}}$
in
$\mathscr{F}_{\lambda }^{\mathrm{oo}}$
in
![]() $\mathscr{F}_{\lambda }$
has codimension
$\mathscr{F}_{\lambda }$
has codimension
![]() $\geq 2$
, so
$\geq 2$
, so
![]() $\pi$
extends to an étale double cover
$\pi$
extends to an étale double cover
![]() $\widetilde{\mathscr{F}}_{\lambda }\rightarrow \mathscr{F}_{\lambda }$
, where
$\widetilde{\mathscr{F}}_{\lambda }\rightarrow \mathscr{F}_{\lambda }$
, where
![]() $\widetilde{\mathscr{F}}_{\lambda }$
is an abelian variety or the disjoint union of two abelian varieties. The morphism
$\widetilde{\mathscr{F}}_{\lambda }$
is an abelian variety or the disjoint union of two abelian varieties. The morphism
![]() $\tilde{\psi }^{\mathrm{o}}_{\lambda }: \widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}\rightarrow \Phi ^{-1}(\tilde{\lambda } )$
is generically of maximal rank. Again by Proposition 5.5, the holomorphic 1-forms on
$\tilde{\psi }^{\mathrm{o}}_{\lambda }: \widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}\rightarrow \Phi ^{-1}(\tilde{\lambda } )$
is generically of maximal rank. Again by Proposition 5.5, the holomorphic 1-forms on
![]() $\widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}$
are closed; hence by pull-back, the same holds for the holomorphic 1-forms on
$\widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}$
are closed; hence by pull-back, the same holds for the holomorphic 1-forms on
![]() $\Phi ^{-1}(\tilde{\lambda } )$
. As in the proof of Corollary 5.2, this implies that
$\Phi ^{-1}(\tilde{\lambda } )$
. As in the proof of Corollary 5.2, this implies that
![]() $\Phi ^{-1}(\tilde{\lambda } )$
is Lagrangian. The second assertion is a basic property of Lagrangian fibres.
$\Phi ^{-1}(\tilde{\lambda } )$
is Lagrangian. The second assertion is a basic property of Lagrangian fibres.
Lemma 5.7
The morphism
![]() $\psi ^{\mathrm{o}}_{\lambda }$
lifts to a morphism
$\psi ^{\mathrm{o}}_{\lambda }$
lifts to a morphism
![]() $\tilde{\psi }^{\mathrm{o}}_{\lambda }:\mathscr{F}^{\mathrm{oo}}_{\lambda }\rightarrow \Phi ^{-1}(\tilde{\lambda } )$
.
$\tilde{\psi }^{\mathrm{o}}_{\lambda }:\mathscr{F}^{\mathrm{oo}}_{\lambda }\rightarrow \Phi ^{-1}(\tilde{\lambda } )$
.
Proof. It suffices to show that the double covering
![]() $\pi :\widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}\rightarrow \mathscr{F}_{\lambda }^{\mathrm{oo}}$
splits.
$\pi :\widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}\rightarrow \mathscr{F}_{\lambda }^{\mathrm{oo}}$
splits.
Assuming the contrary,
![]() $\widetilde{\mathscr{F}}_{\lambda }$
is an abelian variety. By Lemma 5.6
$\widetilde{\mathscr{F}}_{\lambda }$
is an abelian variety. By Lemma 5.6
![]() $H^0(\Phi ^{-1}(\tilde{\lambda }), \Omega ^1)$
has dimension
$H^0(\Phi ^{-1}(\tilde{\lambda }), \Omega ^1)$
has dimension
![]() $n$
. It follows that the pull-back
$n$
. It follows that the pull-back
![]() $(\tilde{\psi }^{\mathrm{o}}_{\lambda })^*: H^0(\Phi ^{-1}(\tilde{\lambda }), \Omega ^1) \rightarrow H^0(\widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}},\Omega ^1)$
is bijective. Since the Galois involution of the double covering
$(\tilde{\psi }^{\mathrm{o}}_{\lambda })^*: H^0(\Phi ^{-1}(\tilde{\lambda }), \Omega ^1) \rightarrow H^0(\widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}},\Omega ^1)$
is bijective. Since the Galois involution of the double covering
![]() $\pi$
acts trivially on holomorphic 1-forms, the same holds for the Galois involution
$\pi$
acts trivially on holomorphic 1-forms, the same holds for the Galois involution
![]() $\iota$
of the double covering
$\iota$
of the double covering
![]() $q_{\lambda }: \Phi ^{-1}(\tilde{\lambda } )\rightarrow (\varphi ^{\mathrm{o}})^{-1}(\lambda )$
.
$q_{\lambda }: \Phi ^{-1}(\tilde{\lambda } )\rightarrow (\varphi ^{\mathrm{o}})^{-1}(\lambda )$
.
Now we observe that the 1-forms on
![]() $\Phi ^{-1}(\tilde{\lambda })$
are ‘pure’; that is, they extend to any smooth projective compactification of
$\Phi ^{-1}(\tilde{\lambda })$
are ‘pure’; that is, they extend to any smooth projective compactification of
![]() $\Phi ^{-1}(\tilde{\lambda } )$
. This follows from the fact that this holds after pull-back to
$\Phi ^{-1}(\tilde{\lambda } )$
. This follows from the fact that this holds after pull-back to
![]() $\widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}$
. But the quotient
$\widetilde{\mathscr{F}}_{\lambda }^{\mathrm{oo}}$
. But the quotient
![]() $\Phi ^{-1}(\tilde{\lambda } )/\iota$
is isomorphic to a Zariski open subset of
$\Phi ^{-1}(\tilde{\lambda } )/\iota$
is isomorphic to a Zariski open subset of
![]() $\varphi ^{-1}(\lambda )$
, which, by Proposition 4.1, has no nonzero holomorphic 1-forms, so any Zariski open subset has no nonzero closed pure holomorphic 1-forms. This contradiction proves the lemma.
$\varphi ^{-1}(\lambda )$
, which, by Proposition 4.1, has no nonzero holomorphic 1-forms, so any Zariski open subset has no nonzero closed pure holomorphic 1-forms. This contradiction proves the lemma.
5.3 Proof of Theorem 5.1
Lemma 5.7 gives a factorisation,
By Proposition 4.1,
![]() $\psi ^{\mathrm{o}}_{\lambda }$
induces a birational morphism,
$\psi ^{\mathrm{o}}_{\lambda }$
induces a birational morphism,
it follows that for some subgroup
![]() $\Gamma '\subset \Gamma$
of index
$\Gamma '\subset \Gamma$
of index
![]() $2$
, the morphism
$2$
, the morphism
![]() $\tilde{\psi _{\lambda }^{\mathrm{o}}}:\mathscr{F}_\lambda ^{\mathrm{oo}}\rightarrow \Phi ^{-1}(\tilde{\lambda } )$
factors through a birational morphism,
$\tilde{\psi _{\lambda }^{\mathrm{o}}}:\mathscr{F}_\lambda ^{\mathrm{oo}}\rightarrow \Phi ^{-1}(\tilde{\lambda } )$
factors through a birational morphism,
By Lemma 5.6, the cotangent bundle of
![]() $\Phi ^{-1}(\tilde{\lambda } )$
is trivial. Therefore, the cotangent bundle of
$\Phi ^{-1}(\tilde{\lambda } )$
is trivial. Therefore, the cotangent bundle of
![]() $\mathscr{F}_{\lambda }^{\mathrm{oo}}/\Gamma '$
is generically generated by its global sections. This implies that
$\mathscr{F}_{\lambda }^{\mathrm{oo}}/\Gamma '$
is generically generated by its global sections. This implies that
![]() $\Gamma '$
acts trivially on holomorphic 1-forms and, hence, is the subgroup
$\Gamma '$
acts trivially on holomorphic 1-forms and, hence, is the subgroup
![]() $\Gamma ^{+}$
of
$\Gamma ^{+}$
of
![]() $\Gamma$
generated by translations, isomorphic to
$\Gamma$
generated by translations, isomorphic to
![]() $(\mathbb{Z}/2\mathbb{Z})^{n-2}$
; thus
$(\mathbb{Z}/2\mathbb{Z})^{n-2}$
; thus
![]() $\mathscr{F}_{\lambda }/\Gamma '$
is an abelian variety
$\mathscr{F}_{\lambda }/\Gamma '$
is an abelian variety
![]() $A$
.
$A$
.
To simplify notation, we write
![]() $A^{\mathrm{o}}:=\mathscr{F}^{\mathrm{oo}}_{\lambda }/\Gamma '$
and
$A^{\mathrm{o}}:=\mathscr{F}^{\mathrm{oo}}_{\lambda }/\Gamma '$
and
![]() $u:=\tilde{\psi }^{\mathrm{o}}_{\lambda, \Gamma '}$
. The rational map
$u:=\tilde{\psi }^{\mathrm{o}}_{\lambda, \Gamma '}$
. The rational map
![]() $u^{-1}: \Phi ^{-1}(\tilde{\lambda } )\dashrightarrow A$
is everywhere defined (e.g. [Reference Birkenhake and LangeBL92, Theorem 4.9.4]), so we have two morphisms
$u^{-1}: \Phi ^{-1}(\tilde{\lambda } )\dashrightarrow A$
is everywhere defined (e.g. [Reference Birkenhake and LangeBL92, Theorem 4.9.4]), so we have two morphisms
whose composition is the inclusion
![]() $A^{\mathrm{o}}\hookrightarrow A$
. Since the tangent bundles of
$A^{\mathrm{o}}\hookrightarrow A$
. Since the tangent bundles of
![]() $A$
and
$A$
and
![]() $\Phi ^{-1}(\tilde{\lambda } )$
are trivial, the determinant of
$\Phi ^{-1}(\tilde{\lambda } )$
are trivial, the determinant of
![]() $Tu: T_{A^{\mathrm{o}}}\rightarrow u^*T _{\Phi ^{-1}(\tilde{\lambda } )}$
is a function on
$Tu: T_{A^{\mathrm{o}}}\rightarrow u^*T _{\Phi ^{-1}(\tilde{\lambda } )}$
is a function on
![]() $A^{\mathrm{o}}$
, hence constant by Proposition 5.5. Therefore,
$A^{\mathrm{o}}$
, hence constant by Proposition 5.5. Therefore,
![]() $u$
is étale and birational, hence an open embedding. This implies that every function on
$u$
is étale and birational, hence an open embedding. This implies that every function on
![]() $\Phi ^{-1}(\widetilde{\lambda })$
is constant (because its restriction to
$\Phi ^{-1}(\widetilde{\lambda })$
is constant (because its restriction to
![]() $A^{\mathrm{o}}$
is constant). Then the previous argument shows that
$A^{\mathrm{o}}$
is constant). Then the previous argument shows that
![]() $u^{-1}$
is also an open embedding, hence
$u^{-1}$
is also an open embedding, hence
![]() $\Phi ^{-1}(\tilde{\lambda } )$
is isomorphic to an open subset of
$\Phi ^{-1}(\tilde{\lambda } )$
is isomorphic to an open subset of
![]() $A$
containing
$A$
containing
![]() $A^{\mathrm{o}}$
. This proves the theorem.
$A^{\mathrm{o}}$
. This proves the theorem.
6. Proof of Proposition 5.5
We keep the notations of Section 4.2. Recall that we have coordinates
![]() $(x_0,\ldots, x_{n+2};y_1,\ldots, y_{n-1})$
on
$(x_0,\ldots, x_{n+2};y_1,\ldots, y_{n-1})$
on
![]() $\mathbb{P}^{2n+1}$
and subspaces
$\mathbb{P}^{2n+1}$
and subspaces
![]() $\mathbb{P}^{n+2}$
and
$\mathbb{P}^{n+2}$
and
![]() $\mathbb{P}^{n-2}$
in
$\mathbb{P}^{n-2}$
in
![]() $\mathbb{P}^{2n+1}$
defined by
$\mathbb{P}^{2n+1}$
defined by
![]() $y=0$
and
$y=0$
and
![]() $x=0$
.
$x=0$
.
Let
![]() $q_1(x)=q_2(x)=0$
be the equations defining
$q_1(x)=q_2(x)=0$
be the equations defining
![]() $X$
in
$X$
in
![]() $\mathbb{P}^{n+2}$
, and let
$\mathbb{P}^{n+2}$
, and let
![]() $R$
be the vector space of quadratic forms in
$R$
be the vector space of quadratic forms in
![]() $y=(y_1,\ldots, y_{n-1})$
. We define an extended family
$y=(y_1,\ldots, y_{n-1})$
. We define an extended family
![]() $\mathscr{X}^{e}\subset \mathbb{P}^{2n+1}\times R^2$
as
$\mathscr{X}^{e}\subset \mathbb{P}^{2n+1}\times R^2$
as
The fibre
![]() $\mathscr{X}^{e}_{r}$
at a point
$\mathscr{X}^{e}_{r}$
at a point
![]() $r=(r_1,r_2)$
of
$r=(r_1,r_2)$
of
![]() $R^2$
is the intersection in
$R^2$
is the intersection in
![]() $\mathbb{P}^{2n+1}$
of the two quadrics
$\mathbb{P}^{2n+1}$
of the two quadrics
![]() $q_1(x)+r_1(y)= q_2(x)+r_2(y)=0$
. Let
$q_1(x)+r_1(y)= q_2(x)+r_2(y)=0$
. Let
![]() $\mathbb{G}$
be the Grassmannian of
$\mathbb{G}$
be the Grassmannian of
![]() $(n-1)$
-planes in
$(n-1)$
-planes in
![]() $\mathbb{P}^{2n+1}$
; we define as before
$\mathbb{P}^{2n+1}$
; we define as before
and the extended rational map
![]() $\psi ^{e}:\mathscr{F}^{e}\dashrightarrow \mathbb{P} T^*X$
, which maps a general
$\psi ^{e}:\mathscr{F}^{e}\dashrightarrow \mathbb{P} T^*X$
, which maps a general
![]() $P\subset \mathscr{X}^{e}_r$
to the pair
$P\subset \mathscr{X}^{e}_r$
to the pair
![]() $(x,H)$
, with
$(x,H)$
, with
![]() $\{x\}=P\cap \mathbb{P}^{n+2}$
and
$\{x\}=P\cap \mathbb{P}^{n+2}$
and
![]() $H=\pi _*T_x(P)$
.
$H=\pi _*T_x(P)$
.
We observe that a general pair
![]() $r=(r_1,r_2)$
of
$r=(r_1,r_2)$
of
![]() $R^2$
is simultaneously diagonalisable, so the restriction of
$R^2$
is simultaneously diagonalisable, so the restriction of
![]() $\psi ^{e}$
to
$\psi ^{e}$
to
![]() $\mathscr{F}^{e}_r$
coincides, for an appropriate choice of the coordinates
$\mathscr{F}^{e}_r$
coincides, for an appropriate choice of the coordinates
![]() $(y_i)$
, with the map
$(y_i)$
, with the map
![]() $\psi _{\lambda }$
that we want to study.
$\psi _{\lambda }$
that we want to study.
Proposition 6.1.
Assume that
![]() $X$
is general.
$X$
is general.
![]() $1.$
Let
$1.$
Let
![]() $\Gamma \subset \mathscr{F}^{e}$
be the locus of points
$\Gamma \subset \mathscr{F}^{e}$
be the locus of points
![]() $(P,r)$
such that either
$(P,r)$
such that either
![]() $\dim P\cap \mathbb{P}^{n+2}\gt 0$
, or
$\dim P\cap \mathbb{P}^{n+2}\gt 0$
, or
![]() $P\cap \mathbb{P}^{n-2}\neq \varnothing$
. Then
$P\cap \mathbb{P}^{n-2}\neq \varnothing$
. Then
![]() $\Gamma$
has codimension
$\Gamma$
has codimension
![]() $\geq 2$
in
$\geq 2$
in
![]() $\mathscr{F}^{e}$
.
$\mathscr{F}^{e}$
.
![]() $2.$
There exists no divisor in
$2.$
There exists no divisor in
![]() $\mathscr{F}^{e}\smallsetminus \Gamma$
that dominates
$\mathscr{F}^{e}\smallsetminus \Gamma$
that dominates
![]() $R^2$
and that is mapped to the base locus
$R^2$
and that is mapped to the base locus
![]() $Z\subset \mathbb{P} T^*X$
by
$Z\subset \mathbb{P} T^*X$
by
![]() $\psi _e$
.
$\psi _e$
.
We claim that this implies Proposition 5.5. Indeed, as just explained above, it suffices to prove the analogue of Proposition 5.5 for
![]() $\psi ^e$
. Next, it is clear that the indeterminacy locus of
$\psi ^e$
. Next, it is clear that the indeterminacy locus of
![]() $\psi ^e$
is contained in
$\psi ^e$
is contained in
![]() $\Gamma$
, so
$\Gamma$
, so
![]() $\psi ^e$
is well-defined on
$\psi ^e$
is well-defined on
![]() $\mathcal{F}^e\smallsetminus \Gamma$
. By Proposition 6.1, (1), it now suffices to prove the analogue of Proposition 5.5 for the restriction of
$\mathcal{F}^e\smallsetminus \Gamma$
. By Proposition 6.1, (1), it now suffices to prove the analogue of Proposition 5.5 for the restriction of
![]() $\psi ^e$
to
$\psi ^e$
to
![]() $\mathcal{F}^e\smallsetminus \Gamma$
. This is exactly the statement of Proposition 6.1, (2).
$\mathcal{F}^e\smallsetminus \Gamma$
. This is exactly the statement of Proposition 6.1, (2).
Proof of Proposition 6.1
: (1) Let
![]() $\mathcal{Q}$
be the vector space of quadratic forms on
$\mathcal{Q}$
be the vector space of quadratic forms on
![]() $\mathbb{P}^{2n+1}$
of the form
$\mathbb{P}^{2n+1}$
of the form
![]() $q(x)+r(y)$
for some quadratic forms
$q(x)+r(y)$
for some quadratic forms
![]() $q$
and
$q$
and
![]() $r$
. For each pair of integers
$r$
. For each pair of integers
![]() $(k,l)$
with
$(k,l)$
with
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $l\geq -1$
, let
$l\geq -1$
, let
![]() $\mathbb{G}_{k,l}$
be the locally closed subvariety of
$\mathbb{G}_{k,l}$
be the locally closed subvariety of
![]() $(n-1)$
-planes
$(n-1)$
-planes
![]() $P\in \mathbb{G}$
such that
$P\in \mathbb{G}$
such that
(We put, by convention,
![]() $l=-1$
if
$l=-1$
if
![]() $P\cap \mathbb{P}^{n-2}=\varnothing$
.) Let
$P\cap \mathbb{P}^{n-2}=\varnothing$
.) Let
and
The general fibre of the projection
![]() $\mathscr{F}^{\mathcal{Q}}\rightarrow \mathcal{Q}^2$
is an abelian variety, and we recover
$\mathscr{F}^{\mathcal{Q}}\rightarrow \mathcal{Q}^2$
is an abelian variety, and we recover
![]() $\mathscr{F}^{e}$
by restricting
$\mathscr{F}^{e}$
by restricting
![]() $\mathscr{F}^{\mathcal{Q}}$
to pairs of quadratic forms of the form
$\mathscr{F}^{\mathcal{Q}}$
to pairs of quadratic forms of the form
![]() $(q_{1}(x)+r_{1}(y), q_{2}(x)+r_{2}(y))$
, with
$(q_{1}(x)+r_{1}(y), q_{2}(x)+r_{2}(y))$
, with
![]() $(q_1(x),q_2(x))$
fixed. Because we assume
$(q_1(x),q_2(x))$
fixed. Because we assume
![]() $X$
general, the pair
$X$
general, the pair
![]() $(q_1(x),q_2(x))$
is general in
$(q_1(x),q_2(x))$
is general in
![]() $\mathcal{Q}^2$
. It thus suffices to prove the result for the larger family
$\mathcal{Q}^2$
. It thus suffices to prove the result for the larger family
![]() $\mathscr{F}^{\mathcal{Q}}$
; that is, to show that
$\mathscr{F}^{\mathcal{Q}}$
; that is, to show that
![]() $\mathscr{F}_{k,l}^{\mathcal{Q}}$
has codimension
$\mathscr{F}_{k,l}^{\mathcal{Q}}$
has codimension
![]() $\geq 2$
in
$\geq 2$
in
![]() $\mathscr{F}^{\mathcal{Q}}$
.
$\mathscr{F}^{\mathcal{Q}}$
.
This is done by a dimension count. For
![]() $P\in \mathbb{G}$
, let
$P\in \mathbb{G}$
, let
![]() $\varphi _P$
be the restriction map
$\varphi _P$
be the restriction map
![]() $\mathcal{Q}\rightarrow H^0(P,\mathscr{O}_{P}(2))$
. The fibre of the projection
$\mathcal{Q}\rightarrow H^0(P,\mathscr{O}_{P}(2))$
. The fibre of the projection
![]() $\mathscr{F}^{\mathcal{Q}}\rightarrow \mathbb{G}$
is the vector space
$\mathscr{F}^{\mathcal{Q}}\rightarrow \mathbb{G}$
is the vector space
![]() $(\mathrm{Ker} \varphi _P)^{\oplus 2}$
. For
$(\mathrm{Ker} \varphi _P)^{\oplus 2}$
. For
![]() $P$
general,
$P$
general,
![]() $\varphi _P$
is surjective: This is the case, for instance, if
$\varphi _P$
is surjective: This is the case, for instance, if
![]() $P$
is contained in the
$P$
is contained in the
![]() $(n+2)$
-plane in
$(n+2)$
-plane in
![]() $\mathbb{P}^{2n+1}$
defined by
$\mathbb{P}^{2n+1}$
defined by
![]() $y_i=x_i\ (i=1,\ldots, n-1)$
. However,
$y_i=x_i\ (i=1,\ldots, n-1)$
. However,
![]() $\varphi _P$
is not surjective for
$\varphi _P$
is not surjective for
![]() $P\in \mathbb{G}_{k,l}$
because the forms
$P\in \mathbb{G}_{k,l}$
because the forms
![]() $r(y)_{|P}$
are singular along
$r(y)_{|P}$
are singular along
![]() $P\cap \mathbb{P}^{n+2}$
and the forms
$P\cap \mathbb{P}^{n+2}$
and the forms
![]() $q(x)_{|P}$
are singular along
$q(x)_{|P}$
are singular along
![]() $P\cap \mathbb{P}^{n-2}$
; this implies that the subspaces
$P\cap \mathbb{P}^{n-2}$
; this implies that the subspaces
![]() $P\cap \mathbb{P}^{n+2}$
and
$P\cap \mathbb{P}^{n+2}$
and
![]() $P\cap \mathbb{P}^{n-2}$
are apolar for all forms in
$P\cap \mathbb{P}^{n-2}$
are apolar for all forms in
![]() $\mathrm{Im} \varphi _P$
. Therefore, the corank of
$\mathrm{Im} \varphi _P$
. Therefore, the corank of
![]() $\varphi _P$
is
$\varphi _P$
is
![]() $\geq (k+1)(l+1)$
, and there is equality when
$\geq (k+1)(l+1)$
, and there is equality when
![]() $P$
is contained in the subspace defined by
$P$
is contained in the subspace defined by
![]() $x_0=\ldots =x_{n+1-k}=y_1=\ldots =y_{n-2-l}=0$
, hence for
$x_0=\ldots =x_{n+1-k}=y_1=\ldots =y_{n-2-l}=0$
, hence for
![]() $P$
general in
$P$
general in
![]() $\mathbb{G}_{k,l}$
. Thus our assertion follows from:
$\mathbb{G}_{k,l}$
. Thus our assertion follows from:
 \begin{align*} \mathrm{codim}(\mathscr{F}^{\mathcal{Q}}_{k,l},\mathscr{F}^{\mathcal{Q}})&=\mathrm{codim}(\mathbb{G}_{k,l},\mathbb{G})-2(k+1)(l+1) \\ &= k(k+1)+(l+1)(l+4)-2(k+1)(l+1)\\ &=(k-l)(k-l-1)+2(l+1)\\ &\geq 2\quad \mbox{if }\ k\geq 1\ \mbox{ or }\ l\geq 0\,. \end{align*}
\begin{align*} \mathrm{codim}(\mathscr{F}^{\mathcal{Q}}_{k,l},\mathscr{F}^{\mathcal{Q}})&=\mathrm{codim}(\mathbb{G}_{k,l},\mathbb{G})-2(k+1)(l+1) \\ &= k(k+1)+(l+1)(l+4)-2(k+1)(l+1)\\ &=(k-l)(k-l-1)+2(l+1)\\ &\geq 2\quad \mbox{if }\ k\geq 1\ \mbox{ or }\ l\geq 0\,. \end{align*}
(2) The base locus
![]() $Z\subset \mathbb{P} T^*X$
has codimension
$Z\subset \mathbb{P} T^*X$
has codimension
![]() $\geq 2$
(Corollary 3.3). Note that
$\geq 2$
(Corollary 3.3). Note that
![]() $\psi ^{e}$
is well-defined in
$\psi ^{e}$
is well-defined in
![]() $\mathscr{F}^{e}\smallsetminus \Gamma$
. If
$\mathscr{F}^{e}\smallsetminus \Gamma$
. If
![]() $\mathscr{D}$
is a codimension
$\mathscr{D}$
is a codimension
![]() $1$
subvariety in
$1$
subvariety in
![]() $\mathscr{F}^{e}\smallsetminus \Gamma$
, with
$\mathscr{F}^{e}\smallsetminus \Gamma$
, with
![]() $\psi ^{e}(\mathscr{D})\subset Z$
, the map
$\psi ^{e}(\mathscr{D})\subset Z$
, the map
![]() $\psi ^{e}$
does not have maximal rank along
$\psi ^{e}$
does not have maximal rank along
![]() $\mathscr{D}$
. This contradicts the following lemma:
$\mathscr{D}$
. This contradicts the following lemma:
Lemma 6.2.
![]() $\psi ^{e}$
has maximal rank on
$\psi ^{e}$
has maximal rank on
![]() $\mathscr{F}^{e}\smallsetminus \Gamma$
.
$\mathscr{F}^{e}\smallsetminus \Gamma$
.
Proof. Let
![]() $(x,H)$
be a point of
$(x,H)$
be a point of
![]() $\mathbb{P} T^*X$
; we view
$\mathbb{P} T^*X$
; we view
![]() $H$
as a hyperplane in the projective tangent space to
$H$
as a hyperplane in the projective tangent space to
![]() $x$
at
$x$
at
![]() $X$
. The fibre of
$X$
. The fibre of
![]() $\psi ^{e}: \mathscr{F}^{e}\smallsetminus \Gamma \rightarrow \mathbb{P} T^*X$
at
$\psi ^{e}: \mathscr{F}^{e}\smallsetminus \Gamma \rightarrow \mathbb{P} T^*X$
at
![]() $(x,H)$
is the locus
$(x,H)$
is the locus
The equations (2) define a smooth, locally closed subvariety
![]() $\mathbb{G}_{x,H}$
of
$\mathbb{G}_{x,H}$
of
![]() $\mathbb{G}$
. Let
$\mathbb{G}$
. Let
![]() $P\in \mathbb{G}_{x,H}$
, and let
$P\in \mathbb{G}_{x,H}$
, and let
![]() $\chi _P: R\rightarrow H^0(P,\mathscr{O}_P(2))$
be the restriction map. We will show below that the image of
$\chi _P: R\rightarrow H^0(P,\mathscr{O}_P(2))$
be the restriction map. We will show below that the image of
![]() $\chi _P$
is the space of quadratic forms on
$\chi _P$
is the space of quadratic forms on
![]() $P$
that are singular at
$P$
that are singular at
![]() $x$
. Since the forms
$x$
. Since the forms
![]() $q_{i|P}$
are singular at
$q_{i|P}$
are singular at
![]() $x$
, this implies that the solutions of (3) form an affine space over
$x$
, this implies that the solutions of (3) form an affine space over
![]() $(\mathrm{Ker} \chi _P)^{\oplus 2}$
. Therefore,
$(\mathrm{Ker} \chi _P)^{\oplus 2}$
. Therefore,
![]() $(\psi ^{e})^{-1}(x,H)$
admits an affine fibration over
$(\psi ^{e})^{-1}(x,H)$
admits an affine fibration over
![]() $\mathbb{G}_{x,H}$
, hence is smooth.
$\mathbb{G}_{x,H}$
, hence is smooth.
Clearly the quadrics in
![]() $\mathrm{Im} \chi _P$
are singular at
$\mathrm{Im} \chi _P$
are singular at
![]() $x$
. To prove the opposite inclusion, choose the coordinates
$x$
. To prove the opposite inclusion, choose the coordinates
![]() $(x_i)$
so that
$(x_i)$
so that
![]() $x=(1,0,\ldots, 0)$
. Since
$x=(1,0,\ldots, 0)$
. Since
![]() $P\cap \mathbb{P}^{n+2}=\{x\}$
, there exist linear forms
$P\cap \mathbb{P}^{n+2}=\{x\}$
, there exist linear forms
![]() $\ell _1,\ldots, \ell _{n+2}$
in the
$\ell _1,\ldots, \ell _{n+2}$
in the
![]() $y_j$
so that
$y_j$
so that
![]() $P$
is defined by
$P$
is defined by
![]() $x_i=\ell _{i}(y)$
for
$x_i=\ell _{i}(y)$
for
![]() $i=1,\ldots, n+2$
. Then a quadratic form on
$i=1,\ldots, n+2$
. Then a quadratic form on
![]() $\mathbb{P}^{2n+1}$
singular at
$\mathbb{P}^{2n+1}$
singular at
![]() $x$
can be written as a form in
$x$
can be written as a form in
![]() $x_1,\ldots, x_{n+2} ;y_1,\ldots, y_{n-1}$
; hence, its restriction to
$x_1,\ldots, x_{n+2} ;y_1,\ldots, y_{n-1}$
; hence, its restriction to
![]() $P$
is in
$P$
is in
![]() $\mathrm{Im} \chi _P$
. This proves the lemma and, hence, also the proposition.
$\mathrm{Im} \chi _P$
. This proves the lemma and, hence, also the proposition.
7. Symmetric tensors: second approach
7.1 The cotangent bundle of a smooth quadric
We consider a smooth quadric
![]() $Q\subset \mathbb{P}^{n+1}$
defined by an equation
$Q\subset \mathbb{P}^{n+1}$
defined by an equation
![]() $q=0$
. Its cotangent bundle
$q=0$
. Its cotangent bundle
![]() $\mathbb{P} T^*Q$
parameterises pairs
$\mathbb{P} T^*Q$
parameterises pairs
![]() $(x,P)$
with
$(x,P)$
with
![]() $x\in Q$
and
$x\in Q$
and
![]() $P$
a
$P$
a
![]() $(n-1)$
-plane tangent to
$(n-1)$
-plane tangent to
![]() $Q$
at
$Q$
at
![]() $x$
. Thus, we get a morphism
$x$
. Thus, we get a morphism
![]() $\gamma$
from
$\gamma$
from
![]() $\mathbb{P} T^*Q$
to the Grassmannian
$\mathbb{P} T^*Q$
to the Grassmannian
![]() $\mathbb{G}$
of
$\mathbb{G}$
of
![]() $(n-1)$
-planes in
$(n-1)$
-planes in
![]() $\mathbb{P}^{n+1}$
, which is the morphism defined by the linear system
$\mathbb{P}^{n+1}$
, which is the morphism defined by the linear system
![]() $\lvert{\mathscr{O}_{\mathbb{P} T^*Q}(1)}\rvert$
. It is birational onto its image, but contracts the subvariety
$\lvert{\mathscr{O}_{\mathbb{P} T^*Q}(1)}\rvert$
. It is birational onto its image, but contracts the subvariety
![]() $\mathscr{C}\subset \mathbb{P} T^*Q$
that consists of pairs
$\mathscr{C}\subset \mathbb{P} T^*Q$
that consists of pairs
![]() $(x,P)$
, such that
$(x,P)$
, such that
![]() $P$
is tangent to
$P$
is tangent to
![]() $Q$
along a line
$Q$
along a line
![]() $\ell \subset Q$
with
$\ell \subset Q$
with
![]() $x\in \ell$
; then
$x\in \ell$
; then
![]() $\gamma ^{-1}(P)$
consists of the pairs
$\gamma ^{-1}(P)$
consists of the pairs
![]() $(x,P)$
with
$(x,P)$
with
![]() $x\in \ell$
.
$x\in \ell$
.
Let
![]() $h_q\in H^0(Q,\mathsf{S}^2 \Omega ^1 _Q(2))$
be the hessian form of
$h_q\in H^0(Q,\mathsf{S}^2 \Omega ^1 _Q(2))$
be the hessian form of
![]() $q$
(§3). Choosing coordinates
$q$
(§3). Choosing coordinates
![]() $(x_i)$
such that
$(x_i)$
such that
![]() $q(x)=\sum x_i^2$
, we have
$q(x)=\sum x_i^2$
, we have
![]() $h_q=\sum (dx_i)^2$
(note that this is, up to a scalar, the unique element of
$h_q=\sum (dx_i)^2$
(note that this is, up to a scalar, the unique element of
![]() $H^0(Q,\mathsf{S}^2 \Omega ^1 _Q(2))$
invariant under
$H^0(Q,\mathsf{S}^2 \Omega ^1 _Q(2))$
invariant under
![]() $\mathrm{Aut}(Q)$
). Then
$\mathrm{Aut}(Q)$
). Then
![]() $h_q(x)$
is non-degenerate at each point
$h_q(x)$
is non-degenerate at each point
![]() $x$
of
$x$
of
![]() $Q$
, so
$Q$
, so
![]() $h_q$
induces an isomorphism
$h_q$
induces an isomorphism
![]() $\Omega ^1 _Q(1)\stackrel{\sim }{\longrightarrow } T_Q(-1)$
, hence also
$\Omega ^1 _Q(1)\stackrel{\sim }{\longrightarrow } T_Q(-1)$
, hence also
![]() $\mathsf{S}^2 \Omega ^1 _Q(2)\stackrel{\sim }{\longrightarrow } \mathsf{S}^2 T_Q(-2)$
. The image in
$\mathsf{S}^2 \Omega ^1 _Q(2)\stackrel{\sim }{\longrightarrow } \mathsf{S}^2 T_Q(-2)$
. The image in
![]() $H^0(Q,\mathsf{S}^2 T_Q(-2))$
of
$H^0(Q,\mathsf{S}^2 T_Q(-2))$
of
![]() $h_q$
by this isomorphism is
$h_q$
by this isomorphism is
![]() $h'_q=\sum \partial _j^2$
. We will view
$h'_q=\sum \partial _j^2$
. We will view
![]() $h'_q$
as an element of
$h'_q$
as an element of
![]() $H^0(\mathbb{P} T^*Q,\mathscr{O}_{\mathbb{P} T^*Q}(2)\otimes p^*\mathscr{O}_Q(-2))$
, where
$H^0(\mathbb{P} T^*Q,\mathscr{O}_{\mathbb{P} T^*Q}(2)\otimes p^*\mathscr{O}_Q(-2))$
, where
![]() $p: \mathbb{P} T^*Q\rightarrow Q$
is the projection.
$p: \mathbb{P} T^*Q\rightarrow Q$
is the projection.
Proposition 7.1.
The divisor of
![]() $h'_q$
is
$h'_q$
is
![]() $\mathscr{C}$
. The projection
$\mathscr{C}$
. The projection
![]() $p_{|\mathscr{C}}:\mathscr{C}\rightarrow Q$
is a smooth quadric fibration, and
$p_{|\mathscr{C}}:\mathscr{C}\rightarrow Q$
is a smooth quadric fibration, and
![]() $\mathscr{C}$
is a prime divisor for
$\mathscr{C}$
is a prime divisor for
![]() $n\geq 3$
.
$n\geq 3$
.
Proof. Let
![]() $x\in Q$
; the hyperplane tangent to
$x\in Q$
; the hyperplane tangent to
![]() $Q$
at
$Q$
at
![]() $x$
cuts out a cone over the smooth quadric
$x$
cuts out a cone over the smooth quadric
![]() $Q_x\subset \mathbb{P}(T_x(Q))$
defined by
$Q_x\subset \mathbb{P}(T_x(Q))$
defined by
![]() $h_q(x)=0$
(Section 3). The isomorphism
$h_q(x)=0$
(Section 3). The isomorphism
![]() $T_x(Q)\stackrel{\sim }{\longrightarrow } T^*_x(Q)$
given by
$T_x(Q)\stackrel{\sim }{\longrightarrow } T^*_x(Q)$
given by
![]() $h_q(x)$
carries
$h_q(x)$
carries
![]() $Q_x$
into the dual quadric
$Q_x$
into the dual quadric
![]() $Q_x^*$
in
$Q_x^*$
in
![]() $\mathbb{P}(T^*_x(Q))$
. On the other hand, a point
$\mathbb{P}(T^*_x(Q))$
. On the other hand, a point
![]() $y\in p^{-1}(x)$
corresponds to a hyperplane
$y\in p^{-1}(x)$
corresponds to a hyperplane
![]() $H_y\subset \mathbb{P}(T_x(Q))$
, and
$H_y\subset \mathbb{P}(T_x(Q))$
, and
![]() $y$
belongs to
$y$
belongs to
![]() $\mathscr{C}$
if and only if
$\mathscr{C}$
if and only if
![]() $H_y$
is tangent to
$H_y$
is tangent to
![]() $Q_x$
; that is, if
$Q_x$
; that is, if
![]() $y\in Q_x^*$
. This proves the equality
$y\in Q_x^*$
. This proves the equality
![]() $\mathscr{C}=\mathrm{div} (h'_q)$
and thus, that the fiber of
$\mathscr{C}=\mathrm{div} (h'_q)$
and thus, that the fiber of
![]() $p_{|\mathscr{C}}:\mathscr{C}\rightarrow Q$
at
$p_{|\mathscr{C}}:\mathscr{C}\rightarrow Q$
at
![]() $x$
is
$x$
is
![]() $Q_x$
, which is smooth and connected if
$Q_x$
, which is smooth and connected if
![]() $n\geq 3$
.
$n\geq 3$
.
Remark 7.2 The variety
![]() $\mathscr{C}$
is an example of a total dual VMRT [Reference Liu and ShaoHLS22]. For the proof of the theorem, we will combine this tool with the birational transformation of
$\mathscr{C}$
is an example of a total dual VMRT [Reference Liu and ShaoHLS22]. For the proof of the theorem, we will combine this tool with the birational transformation of
![]() $\mathbb{P} T^* X$
defined by a double cover. (Compare with [Reference Anella and HöringAH23]).
$\mathbb{P} T^* X$
defined by a double cover. (Compare with [Reference Anella and HöringAH23]).
We will have to consider the following situation: Let
![]() $Q'$
be another quadric in
$Q'$
be another quadric in
![]() $\mathbb{P}^{n+1}$
, such that the intersection
$\mathbb{P}^{n+1}$
, such that the intersection
![]() $B:=Q\cap Q'$
is a smooth hypersurface in
$B:=Q\cap Q'$
is a smooth hypersurface in
![]() $Q$
. The surjection
$Q$
. The surjection
![]() $T_{Q}\rightarrow N_{B/Q}$
gives a section of
$T_{Q}\rightarrow N_{B/Q}$
gives a section of
![]() $\mathbb{P} T^*Q$
over
$\mathbb{P} T^*Q$
over
![]() $B$
, hence an embedding
$B$
, hence an embedding
![]() $s:B\hookrightarrow \mathbb{P} T^*Q$
.
$s:B\hookrightarrow \mathbb{P} T^*Q$
.
Lemma 7.3.
The image
![]() $s(B)$
is not contained in
$s(B)$
is not contained in
![]() $\mathscr{C}$
.
$\mathscr{C}$
.
Proof. Let
![]() $x\in B$
. The point
$x\in B$
. The point
![]() $s(x)$
in
$s(x)$
in
![]() $\mathbb{P}(T_x^*(Q))$
corresponds to the hyperplane image of
$\mathbb{P}(T_x^*(Q))$
corresponds to the hyperplane image of
![]() $T_x(B)$
in
$T_x(B)$
in
![]() $T_{x}(Q)$
; we must therefore show that this hyperplane is not tangent to the quadric
$T_{x}(Q)$
; we must therefore show that this hyperplane is not tangent to the quadric
![]() $Q_x:=h_q(x)$
. In terms of projective space, this means that the projective tangent space to
$Q_x:=h_q(x)$
. In terms of projective space, this means that the projective tangent space to
![]() $Q'$
at
$Q'$
at
![]() $x$
is not tangent, at a smooth point
$x$
is not tangent, at a smooth point
![]() $y$
, to the cone cut out on
$y$
, to the cone cut out on
![]() $Q$
by the projective tangent space to
$Q$
by the projective tangent space to
![]() $Q'$
at
$Q'$
at
![]() $x$
.
$x$
.
Suppose that this is the case, with
![]() $y=(y_0,\ldots, y_{n+1})$
. We can assume that
$y=(y_0,\ldots, y_{n+1})$
. We can assume that
![]() $Q'$
is defined by
$Q'$
is defined by
![]() $\sum \alpha _i x_i^2=0$
, with
$\sum \alpha _i x_i^2=0$
, with
![]() $\alpha _i\in \mathbb{C}$
distinct. Then the (projective) tangent space to
$\alpha _i\in \mathbb{C}$
distinct. Then the (projective) tangent space to
![]() $Q'$
at
$Q'$
at
![]() $x$
, given by
$x$
, given by
![]() $\sum (\alpha _ix_i)\xi _i=0$
, must coincide with the tangent space to
$\sum (\alpha _ix_i)\xi _i=0$
, must coincide with the tangent space to
![]() $Q$
at
$Q$
at
![]() $y$
, given by
$y$
, given by
![]() $\sum y_i\xi _i=0$
. This implies
$\sum y_i\xi _i=0$
. This implies
![]() $y=(\alpha _0x_0,\ldots, \alpha _{n+1}x_{n+1})$
. Thus the point
$y=(\alpha _0x_0,\ldots, \alpha _{n+1}x_{n+1})$
. Thus the point
![]() $x$
must satisfy
$x$
must satisfy
If these relations hold for all
![]() $x$
in
$x$
in
![]() $B$
, the quadric
$B$
, the quadric
![]() $\sum \alpha _i^2 x_i^2=0$
must belong to the pencil spanned by
$\sum \alpha _i^2 x_i^2=0$
must belong to the pencil spanned by
![]() $Q$
and
$Q$
and
![]() $Q'$
. This means that there exist scalars
$Q'$
. This means that there exist scalars
![]() $\lambda, \mu, \nu$
such that
$\lambda, \mu, \nu$
such that
which is impossible since the
![]() $\alpha _i$
are distinct. Therefore, there exists
$\alpha _i$
are distinct. Therefore, there exists
![]() $x\in B$
such that
$x\in B$
such that
![]() $s(x)\notin \mathscr{C}$
.
$s(x)\notin \mathscr{C}$
.
7.2 Explicit description of symmetric tensors
We keep the notation of the previous sections:
![]() $X\subset \mathbb{P}=\mathbb{P}^{n+2}$
is defined by
$X\subset \mathbb{P}=\mathbb{P}^{n+2}$
is defined by
![]() $q_1=q_2=0$
, and with
$q_1=q_2=0$
, and with
 \begin{equation*} q_1 = \sum _{i=0}^{n+2} x_i^2, \qquad q_2 = \sum _{i=0}^{n+2} \mu _i x_i^2 \qquad \mbox {with } \mu _i \in \mathbb {C} \mbox { distinct}. \end{equation*}
\begin{equation*} q_1 = \sum _{i=0}^{n+2} x_i^2, \qquad q_2 = \sum _{i=0}^{n+2} \mu _i x_i^2 \qquad \mbox {with } \mu _i \in \mathbb {C} \mbox { distinct}. \end{equation*}
We put
![]() $\partial _i:=\dfrac{\partial }{\partial x_i} \,\cdot$
We have an exact sequence
$\partial _i:=\dfrac{\partial }{\partial x_i} \,\cdot$
We have an exact sequence
where
![]() $dq_i$
maps the restriction of a vector field
$dq_i$
maps the restriction of a vector field
![]() $V$
on
$V$
on
![]() $\mathbb{P}$
to
$\mathbb{P}$
to
![]() $V\cdot q_i$
. This gives the exact sequence of symmetric tensors
$V\cdot q_i$
. This gives the exact sequence of symmetric tensors
where
![]() $dq_i(V_1V_2)=(V_1\cdot q_i)V_2+(V_2\cdot q_i)V_1$
for
$dq_i(V_1V_2)=(V_1\cdot q_i)V_2+(V_2\cdot q_i)V_1$
for
![]() $V_1,V_2$
in
$V_1,V_2$
in
![]() $H^0(X, T_{\mathbb{P}|X})$
.
$H^0(X, T_{\mathbb{P}|X})$
.
Proposition 7.4.
The quadratic vector fields
 $\displaystyle s_i:=\sum _{j\neq i} \dfrac{(x_i\partial _j-x_j\partial _i)^2}{\mu _j-\mu _i}$
in
$\displaystyle s_i:=\sum _{j\neq i} \dfrac{(x_i\partial _j-x_j\partial _i)^2}{\mu _j-\mu _i}$
in
![]() $H^0(X, \mathsf{S}^2 T_{\mathbb{P}|X})$
belong to the image of
$H^0(X, \mathsf{S}^2 T_{\mathbb{P}|X})$
belong to the image of
![]() $H^0(X, \mathsf{S}^2 T_{X})$
.
$H^0(X, \mathsf{S}^2 T_{X})$
.
Proof. According to the exact sequence (4), we have to prove
![]() $dq_1(s_i)=dq_2(s_i)=0$
.
$dq_1(s_i)=dq_2(s_i)=0$
.
We have
![]() $(x_i\partial _j-x_j\partial _i)\cdot q_1=0$
; hence,
$(x_i\partial _j-x_j\partial _i)\cdot q_1=0$
; hence,
![]() $dq_1(s_i)=0$
and
$dq_1(s_i)=0$
and
![]() $dq_2(x_i\partial _j-x_j\partial _i,x_i\partial _j-x_j\partial _i)= 4(\mu _j-\mu _i)x_ix_j(x_i\partial _j-x_j\partial _i)$
. Hence, using
$dq_2(x_i\partial _j-x_j\partial _i,x_i\partial _j-x_j\partial _i)= 4(\mu _j-\mu _i)x_ix_j(x_i\partial _j-x_j\partial _i)$
. Hence, using
![]() $\sum x_j\partial _j=0$
and
$\sum x_j\partial _j=0$
and
![]() $q_{1|X}=0$
,
$q_{1|X}=0$
,
In the rest of this article, we will consider the
![]() $s_i$
to be elements of
$s_i$
to be elements of
![]() $H^0(X, \mathsf{S}^2 T_{X})$
.
$H^0(X, \mathsf{S}^2 T_{X})$
.
7.3 The double cover
Let
![]() $p_0: \mathbb{P}^{n+2}\dashrightarrow \mathbb{P}^{n+1}$
be the projection
$p_0: \mathbb{P}^{n+2}\dashrightarrow \mathbb{P}^{n+1}$
be the projection
![]() $(x_0,\ldots, x_{n+2})\mapsto (x_1,\ldots, x_{n+2})$
. The image
$(x_0,\ldots, x_{n+2})\mapsto (x_1,\ldots, x_{n+2})$
. The image
![]() $p_0(X)$
is the smooth quadric
$p_0(X)$
is the smooth quadric
![]() $Q$
in
$Q$
in
![]() $\mathbb{P}^{n+1}$
defined by
$\mathbb{P}^{n+1}$
defined by
 \begin{equation*}\sum _{i=1}^{n+2}(\mu _i-\mu _0)x_{i}^{2}=0\,.\end{equation*}
\begin{equation*}\sum _{i=1}^{n+2}(\mu _i-\mu _0)x_{i}^{2}=0\,.\end{equation*}
The restriction
![]() $\pi : X\rightarrow Q$
of
$\pi : X\rightarrow Q$
of
![]() $p_0$
is a double covering that is branched along the subvariety
$p_0$
is a double covering that is branched along the subvariety
![]() $B\subset Q$
defined by
$B\subset Q$
defined by
 \begin{equation*}\sum _{i=1}^{n+2} x_i^2=\sum _{i=1}^{n+2}\mu _i x_i^2=0\,.\end{equation*}
\begin{equation*}\sum _{i=1}^{n+2} x_i^2=\sum _{i=1}^{n+2}\mu _i x_i^2=0\,.\end{equation*}
It is a smooth complete intersection of 2 quadrics in
![]() $\mathbb{P}^{n+1}$
. The ramification locus
$\mathbb{P}^{n+1}$
. The ramification locus
![]() $R\subset X$
of
$R\subset X$
of
![]() $\pi$
(isomorphic to
$\pi$
(isomorphic to
![]() $B$
) is the hyperplane section
$B$
) is the hyperplane section
![]() $x_0=0$
of
$x_0=0$
of
![]() $X$
.
$X$
.
The tangent map of
![]() $\pi :X\rightarrow Q$
gives a morphism,
$\pi :X\rightarrow Q$
gives a morphism,
which is an isomorphism outside of
![]() $R$
. Consider the normal exact sequence
$R$
. Consider the normal exact sequence
The involution
![]() $\iota :(x_0,\ldots, x_{n+2})\mapsto (-x_0,x_1,\ldots, x_{n+2})$
acts on
$\iota :(x_0,\ldots, x_{n+2})\mapsto (-x_0,x_1,\ldots, x_{n+2})$
acts on
![]() $T_{X|R}$
; this splits the exact sequence, giving a decomposition
$T_{X|R}$
; this splits the exact sequence, giving a decomposition
into eigenspaces for the eigenvalues
![]() $+1$
and
$+1$
and
![]() $-1$
. Let
$-1$
. Let
![]() $\rho : T_{X|R}\rightarrow T_R$
be the projection on the first summand. We deduce from
$\rho : T_{X|R}\rightarrow T_R$
be the projection on the first summand. We deduce from
![]() $\rho$
a sequence of homomorphisms
$\rho$
a sequence of homomorphisms
Since
![]() $\iota _*\partial _0=-\partial _0$
and
$\iota _*\partial _0=-\partial _0$
and
![]() $\iota _*\partial _j=\partial _j$
for
$\iota _*\partial _j=\partial _j$
for
![]() $j\gt 0$
, we have
$j\gt 0$
, we have
 \begin{equation} h^2(s_0)=0\quad \mbox{and}\quad h^2(s_i)=\sum _{j\gt 0 \atop j\neq i} \dfrac{(x_i\partial _j-x_j\partial _i)^2}{\mu _j-\mu _i}\quad \mbox{for }i\gt 0\, \end{equation}
\begin{equation} h^2(s_0)=0\quad \mbox{and}\quad h^2(s_i)=\sum _{j\gt 0 \atop j\neq i} \dfrac{(x_i\partial _j-x_j\partial _i)^2}{\mu _j-\mu _i}\quad \mbox{for }i\gt 0\, \end{equation}
in other words,
![]() $h^2$
maps
$h^2$
maps
![]() $s_1,\ldots, s_{n+2}$
to the elements
$s_1,\ldots, s_{n+2}$
to the elements
![]() $\hat{s}_1,\ldots, \hat{s}_{n+2}$
of
$\hat{s}_1,\ldots, \hat{s}_{n+2}$
of
![]() $H^0(R, \mathsf{S}^2T_R)$
constructed in Proposition 7.2.1 applied to
$H^0(R, \mathsf{S}^2T_R)$
constructed in Proposition 7.2.1 applied to
![]() $R$
.
$R$
.
Let
![]() $\pi ^*\mathbb{P} T^*Q$
be the pull-back under
$\pi ^*\mathbb{P} T^*Q$
be the pull-back under
![]() $\pi$
of the projective bundle
$\pi$
of the projective bundle
![]() $\mathbb{P} T^*Q\rightarrow Q$
. The homomorphism
$\mathbb{P} T^*Q\rightarrow Q$
. The homomorphism
![]() $\tau :T_X\rightarrow \pi ^*T_Q$
gives rise to the birational map
$\tau :T_X\rightarrow \pi ^*T_Q$
gives rise to the birational map
![]() $g: \pi ^*\mathbb{P} T^*Q\dashrightarrow \mathbb{P} T^*X$
. Following the geometric description of the tangent map as an elementary transformation of vector bundles in the sense of Maruyama in [Reference MaruyamaMar72] and [Reference MaruyamaMar73, Corollary 1.1.1], one has a commutative diagram
$g: \pi ^*\mathbb{P} T^*Q\dashrightarrow \mathbb{P} T^*X$
. Following the geometric description of the tangent map as an elementary transformation of vector bundles in the sense of Maruyama in [Reference MaruyamaMar72] and [Reference MaruyamaMar73, Corollary 1.1.1], one has a commutative diagram

where
![]() $p$
and
$p$
and
![]() $q$
are the canonical projections;
$q$
are the canonical projections;
![]() $\nu : \Gamma \rightarrow \mathbb{P} T^* X$
is the blow-up along the subspace
$\nu : \Gamma \rightarrow \mathbb{P} T^* X$
is the blow-up along the subspace
![]() $\mathbb{P} T^* R \subset \mathbb{P} T^* X$
defined by the projection
$\mathbb{P} T^* R \subset \mathbb{P} T^* X$
defined by the projection
![]() $\rho$
; and
$\rho$
; and
![]() $\mu :\Gamma \rightarrow \pi ^*\mathbb{P} T^*Q$
is the blow-up of the image
$\mu :\Gamma \rightarrow \pi ^*\mathbb{P} T^*Q$
is the blow-up of the image
![]() $B'$
of the embedding
$B'$
of the embedding
![]() $B\hookrightarrow \pi ^*\mathbb{P} T^*Q$
deduced from the surjective homomorphism
$B\hookrightarrow \pi ^*\mathbb{P} T^*Q$
deduced from the surjective homomorphism
![]() $\pi ^*T_Q\rightarrow \pi ^*N_{B/X}$
.
$\pi ^*T_Q\rightarrow \pi ^*N_{B/X}$
.
Let
![]() $E_{\mu }$
be the exceptional divisor of
$E_{\mu }$
be the exceptional divisor of
![]() $\mu$
. By [Reference MaruyamaMar73, Theorem 1.1], there is an isomorphism
$\mu$
. By [Reference MaruyamaMar73, Theorem 1.1], there is an isomorphism
as well as the equality
7.4 The divisor of
 $\boldsymbol{{s}}_{\textbf{0}}$
$\boldsymbol{{s}}_{\textbf{0}}$
We now consider the divisor
![]() $\mathscr{C}\subset \mathbb{P} T^*Q$
defined in (7.1) and the cartesian diagram
$\mathscr{C}\subset \mathbb{P} T^*Q$
defined in (7.1) and the cartesian diagram

Set
![]() $\mathscr{C}^{\,\prime}:= \pi '^{-1}(\mathscr{C})$
. The projection
$\mathscr{C}^{\,\prime}:= \pi '^{-1}(\mathscr{C})$
. The projection
![]() $\mathscr{C}^{\,\prime}\rightarrow X$
is again a smooth quadric fibration, so
$\mathscr{C}^{\,\prime}\rightarrow X$
is again a smooth quadric fibration, so
![]() $\mathscr{C}^{\,\prime}$
is smooth and connected for
$\mathscr{C}^{\,\prime}$
is smooth and connected for
![]() $n\geq 3$
.
$n\geq 3$
.
Recall that we have defined the element
 $\displaystyle s_0:=\sum _{j=1}^{n+2} \dfrac{(x_0\partial _j-x_j\partial _0)^2}{\mu _j-\mu _0} \in H^0(X,\mathsf{S}^2T_X)$
(7.2). We will now view
$\displaystyle s_0:=\sum _{j=1}^{n+2} \dfrac{(x_0\partial _j-x_j\partial _0)^2}{\mu _j-\mu _0} \in H^0(X,\mathsf{S}^2T_X)$
(7.2). We will now view
![]() $s_0$
as an element of
$s_0$
as an element of
![]() $H^0(\mathbb{P} T^*X,\mathscr{O}(2))$
.
$H^0(\mathbb{P} T^*X,\mathscr{O}(2))$
.
Proposition 7.5
Assume
![]() $n\geq 3$
. We have
$n\geq 3$
. We have
![]() $g_*\mathscr{C}^{\,\prime}=\mathrm{div}(s_0)$
.
$g_*\mathscr{C}^{\,\prime}=\mathrm{div}(s_0)$
.
Proof. We first show that
![]() $g_*\mathscr{C}^{\,\prime}\in \lvert{\mathscr{O}_{\mathbb{P} T^*X}(2)}\rvert$
. By Proposition 7.1 we have
$g_*\mathscr{C}^{\,\prime}\in \lvert{\mathscr{O}_{\mathbb{P} T^*X}(2)}\rvert$
. By Proposition 7.1 we have
![]() $\mathscr{C}^{\,\prime}\in \lvert{\mathscr{O}_{\pi ^*\mathbb{P} T^*Q}(2)\otimes p^*\mathscr{O}_X(-2)}\rvert$
. Using (7), (8) and the projection formula, we get the linear equivalences
$\mathscr{C}^{\,\prime}\in \lvert{\mathscr{O}_{\pi ^*\mathbb{P} T^*Q}(2)\otimes p^*\mathscr{O}_X(-2)}\rvert$
. Using (7), (8) and the projection formula, we get the linear equivalences
Thus, it is enough to prove that
![]() $\nu _*\mu ^*\mathscr{C}^{\,\prime}$
is irreducible. Since
$\nu _*\mu ^*\mathscr{C}^{\,\prime}$
is irreducible. Since
![]() $\mathscr{C}^{\,\prime}$
is irreducible and
$\mathscr{C}^{\,\prime}$
is irreducible and
![]() $\mu$
is the blow-up along
$\mu$
is the blow-up along
![]() $B'\subset \pi ^*\mathbb{P} T^*Q$
, it suffices to show that
$B'\subset \pi ^*\mathbb{P} T^*Q$
, it suffices to show that
![]() $B'$
is not contained in
$B'$
is not contained in
![]() $\mathscr{C}^{\,\prime}$
. If this is the case, then we have
$\mathscr{C}^{\,\prime}$
. If this is the case, then we have
![]() $\pi '(B')\subset \pi ' (\mathscr{C}^{\,\prime})=\mathscr{C}$
. But
$\pi '(B')\subset \pi ' (\mathscr{C}^{\,\prime})=\mathscr{C}$
. But
![]() $\pi '(B')=s(B)$
, where
$\pi '(B')=s(B)$
, where
![]() $s: B\hookrightarrow \mathbb{P} T^*Q$
is the embedding defined by the surjective homomorphism
$s: B\hookrightarrow \mathbb{P} T^*Q$
is the embedding defined by the surjective homomorphism
![]() $T_Q\rightarrow N_{B/Q}$
. Then the result follows from Lemma 7.3.
$T_Q\rightarrow N_{B/Q}$
. Then the result follows from Lemma 7.3.
Since
![]() $g_*\mathscr{C}^{\,\prime}$
and
$g_*\mathscr{C}^{\,\prime}$
and
![]() $\mathrm{div}(s_0)$
are linearly equivalent effective divisors and
$\mathrm{div}(s_0)$
are linearly equivalent effective divisors and
![]() $g_*\mathscr{C}^{\,\prime}$
is irreducible, it suffices to show that their restrictions to
$g_*\mathscr{C}^{\,\prime}$
is irreducible, it suffices to show that their restrictions to
![]() $\mathbb{P} T_x^*(X)$
coincide at a general point
$\mathbb{P} T_x^*(X)$
coincide at a general point
![]() $x\in X$
.
$x\in X$
.
Fix a point
![]() $x=(x_0,\dots, x_{n+2})\in X\smallsetminus R$
so that
$x=(x_0,\dots, x_{n+2})\in X\smallsetminus R$
so that
![]() $x_0\not =0$
. Then the tangent map
$x_0\not =0$
. Then the tangent map
![]() $T\pi (x): T_x(X)\rightarrow T_{\pi (x)}(Q)$
is an isomorphism; in diagram (6), the maps
$T\pi (x): T_x(X)\rightarrow T_{\pi (x)}(Q)$
is an isomorphism; in diagram (6), the maps
![]() $\mu, \nu$
and
$\mu, \nu$
and
![]() $g$
restricted over the fibres at
$g$
restricted over the fibres at
![]() $x$
are all isomorphisms. Let us show that
$x$
are all isomorphisms. Let us show that
![]() $\mathscr{C}^{\,\prime}$
and
$\mathscr{C}^{\,\prime}$
and
![]() $T\pi (\mathrm{div}(s_0))$
define the same quadric in
$T\pi (\mathrm{div}(s_0))$
define the same quadric in
![]() $\mathbb{P} (T_{\pi (x)}(Q))$
.
$\mathbb{P} (T_{\pi (x)}(Q))$
.
Note that
![]() $\mathscr{C}^{\,\prime}\cap \mathbb{P} (T^*_{x}(X))=\mathscr{C}\cap \mathbb{P} (T^*_{\pi (x)}(Q))$
is the quadric defined by the element
$\mathscr{C}^{\,\prime}\cap \mathbb{P} (T^*_{x}(X))=\mathscr{C}\cap \mathbb{P} (T^*_{\pi (x)}(Q))$
is the quadric defined by the element
![]() $h'_q$
of (7.1). In the coordinates
$h'_q$
of (7.1). In the coordinates
![]() $(z_i)$
defined by
$(z_i)$
defined by
![]() $z_i= (\mu _i-\mu _0)^{1/2}x_i$
, the equation of
$z_i= (\mu _i-\mu _0)^{1/2}x_i$
, the equation of
![]() $Q$
is
$Q$
is
 $\displaystyle \sum _{j=1}^{n+2}z_j^2=0$
, so
$\displaystyle \sum _{j=1}^{n+2}z_j^2=0$
, so
 \begin{equation*}h'_q=\sum _{j=1}^{n+2}\bigl (\dfrac {\partial }{\partial z_j}\bigr )^2= \sum _{j=1}^{n+2}\dfrac {\partial _j^2}{\mu _j-\mu _0}\ \cdot \end{equation*}
\begin{equation*}h'_q=\sum _{j=1}^{n+2}\bigl (\dfrac {\partial }{\partial z_j}\bigr )^2= \sum _{j=1}^{n+2}\dfrac {\partial _j^2}{\mu _j-\mu _0}\ \cdot \end{equation*}
On the other hand, since
![]() $\pi (x_0,\ldots, x_{n+2})=(x_1,\ldots, x_{n+2})$
, we have
$\pi (x_0,\ldots, x_{n+2})=(x_1,\ldots, x_{n+2})$
, we have
![]() $T\pi (\partial _0)=0$
and
$T\pi (\partial _0)=0$
and
![]() $T\pi (\partial _j)=\partial _j$
for
$T\pi (\partial _j)=\partial _j$
for
![]() $j\gt 0$
; hence,
$j\gt 0$
; hence,
 \begin{equation*}T\pi (s_0)=x_0^2\, \sum _{j=1}^{n+2}\dfrac {\partial _j^2}{\mu _j-\mu _0}\ \cdot \end{equation*}
\begin{equation*}T\pi (s_0)=x_0^2\, \sum _{j=1}^{n+2}\dfrac {\partial _j^2}{\mu _j-\mu _0}\ \cdot \end{equation*}
Since
![]() $x_0\neq 0$
, this proves the proposition.
$x_0\neq 0$
, this proves the proposition.
7.5 Proof of part (a) of the theorem
Suppose now that
![]() $n \geq 3$
. Consider the double cover
$n \geq 3$
. Consider the double cover
![]() $ \pi : X \rightarrow Q$
and the ramification divisor
$ \pi : X \rightarrow Q$
and the ramification divisor
![]() $R \subset X$
. The restriction maps
$R \subset X$
. The restriction maps
![]() $h^k$
defined in Section 7.3 yield a homomorphism of graded
$h^k$
defined in Section 7.3 yield a homomorphism of graded
![]() $\mathbb{C}$
-algebras
$\mathbb{C}$
-algebras
Proposition 7.6
The kernel
![]() $\mathscr{I}$
of
$\mathscr{I}$
of
![]() $h$
is the ideal generated by
$h$
is the ideal generated by
![]() $s_0$
.
$s_0$
.
Proof. Since
![]() $\mathscr{I}$
is a homogeneous ideal, it suffices to prove that every homogeneous element
$\mathscr{I}$
is a homogeneous ideal, it suffices to prove that every homogeneous element
![]() $s\in \mathscr{I}$
can be written as
$s\in \mathscr{I}$
can be written as
![]() $s=s' s_0$
for some element
$s=s' s_0$
for some element
![]() $s'\in S(X)$
.
$s'\in S(X)$
.
Choose an element
![]() $s \in \mathscr{I}$
of degree
$s \in \mathscr{I}$
of degree
![]() $k$
. This element corresponds to an effective Cartier divisor
$k$
. This element corresponds to an effective Cartier divisor
![]() $G$
in the linear system
$G$
in the linear system
![]() $|\mathscr{O}_{\mathbb{P} T^* X}(k)|$
. Recall the commutative diagram (6):
$|\mathscr{O}_{\mathbb{P} T^* X}(k)|$
. Recall the commutative diagram (6):

Choose
![]() $ \hat{G} :=\mu _* \nu ^* G\subset \pi ^*\mathbb{P} T^*Q$
. By (7),
$ \hat{G} :=\mu _* \nu ^* G\subset \pi ^*\mathbb{P} T^*Q$
. By (7),
![]() $\hat{G}$
belongs to the linear system
$\hat{G}$
belongs to the linear system
![]() $\lvert{\mathscr{O}_{\pi ^*\mathbb{P} T^*Q}(k)}\rvert$
.
$\lvert{\mathscr{O}_{\pi ^*\mathbb{P} T^*Q}(k)}\rvert$
.
Here is the key observation: Since
![]() $s \in \mathscr{I}$
, the divisor
$s \in \mathscr{I}$
, the divisor
![]() $ \hat{G} \subset \pi ^*\mathbb{P} T^*Q$
contains
$ \hat{G} \subset \pi ^*\mathbb{P} T^*Q$
contains
![]() $p^* R$
. Indeed, since
$p^* R$
. Indeed, since
![]() $(\pi ^*T_Q)_{|R}$
is invariant under
$(\pi ^*T_Q)_{|R}$
is invariant under
![]() $\iota$
, the homomorphism
$\iota$
, the homomorphism
![]() $\tau ^{} _{|R}$
factors as
$\tau ^{} _{|R}$
factors as
Therefore, we have a commutative diagram,

and
![]() $\mathsf{S}^k\tau (s)$
vanishes on
$\mathsf{S}^k\tau (s)$
vanishes on
![]() $R$
. But
$R$
. But
![]() $\hat{G}$
is the divisor of
$\hat{G}$
is the divisor of
![]() $\mathsf{S}^k\tau (s)$
, viewed as a section of
$\mathsf{S}^k\tau (s)$
, viewed as a section of
![]() $\mathscr{O}_{\pi ^*\mathbb{P} T^*Q}(k)$
; hence,
$\mathscr{O}_{\pi ^*\mathbb{P} T^*Q}(k)$
; hence,
![]() $\hat{G}$
contains
$\hat{G}$
contains
![]() $p^*R$
.
$p^*R$
.
Now we want to show that the divisor
![]() $\mathscr{C}^{\,\prime}\subset \pi ^*\mathbb{P} T^*Q$
is a component of
$\mathscr{C}^{\,\prime}\subset \pi ^*\mathbb{P} T^*Q$
is a component of
![]() $\hat{G}-p^*R$
. Recall from (7.1) that
$\hat{G}-p^*R$
. Recall from (7.1) that
![]() $\mathscr{C}$
is the union of the lines
$\mathscr{C}$
is the union of the lines
![]() $\ell$
that are contracted by the morphism
$\ell$
that are contracted by the morphism
![]() $\gamma : \mathbb{P} T^*Q\rightarrow \mathbb{G}$
and that
$\gamma : \mathbb{P} T^*Q\rightarrow \mathbb{G}$
and that
![]() $c_1(\mathscr{O}_{\mathbb{P} T^*Q}(1))\cdot \ell =0$
. Thus the curves
$c_1(\mathscr{O}_{\mathbb{P} T^*Q}(1))\cdot \ell =0$
. Thus the curves
![]() $\ell ':=\pi '^*\ell$
cover
$\ell ':=\pi '^*\ell$
cover
![]() $\mathscr{C}^{\,\prime}$
and satisfy
$\mathscr{C}^{\,\prime}$
and satisfy
![]() $c_1(\mathscr{O}_{\pi ^*\mathbb{P} T^*Q}(1))\cdot \ell '=0$
. On the other hand, the divisor
$c_1(\mathscr{O}_{\pi ^*\mathbb{P} T^*Q}(1))\cdot \ell '=0$
. On the other hand, the divisor
![]() $R\subset X$
is a hyperplane section, so
$R\subset X$
is a hyperplane section, so
![]() $p^*R\cdot \ell '=R\cdot p_*\ell '\gt 0$
. Therefore,
$p^*R\cdot \ell '=R\cdot p_*\ell '\gt 0$
. Therefore,
so
![]() $\mathscr{C}^{\,\prime}$
is a component of
$\mathscr{C}^{\,\prime}$
is a component of
![]() $\hat{G}$
. Thus,
$\hat{G}$
. Thus,
![]() $g_*\mathscr{C}^{\,\prime}$
is a component of
$g_*\mathscr{C}^{\,\prime}$
is a component of
![]() $G$
. Since
$G$
. Since
![]() $g_*\mathscr{C}^{\,\prime}=\mathrm{div}(s_0)$
by Proposition 7.5, this proves the proposition.
$g_*\mathscr{C}^{\,\prime}=\mathrm{div}(s_0)$
by Proposition 7.5, this proves the proposition.
The following proposition implies part (a) of our main theorem:
Proposition 7.7.
Assume
![]() $n\geq 2$
. For any choice of indices
$n\geq 2$
. For any choice of indices
![]() $0\leq i_1\lt \ldots \lt i_n\leq n+2$
, the homomorphism
$0\leq i_1\lt \ldots \lt i_n\leq n+2$
, the homomorphism
![]() $\mathbb{C}[t_1,\ldots, t_{n}]\rightarrow S(X)$
, which maps
$\mathbb{C}[t_1,\ldots, t_{n}]\rightarrow S(X)$
, which maps
![]() $t_j$
to
$t_j$
to
![]() $s_{i_{j}}$
, with
$s_{i_{j}}$
, with
![]() $\deg (t_i)=2$
, is an isomorphism of graded
$\deg (t_i)=2$
, is an isomorphism of graded
![]() $\mathbb{C}$
-algebras.
$\mathbb{C}$
-algebras.
Proof. We argue by induction on
![]() $n$
. The statement for
$n$
. The statement for
![]() $n=2$
follows from [Reference De Oliveira and LangdonDOL19, Theorem 5.1], except for the fact that any two of the
$n=2$
follows from [Reference De Oliveira and LangdonDOL19, Theorem 5.1], except for the fact that any two of the
![]() $s_i$
generate
$s_i$
generate
![]() $H^0(X,\mathsf{S}^2T_X)$
. Up to the permuting of the coordinates, it suffices to prove that
$H^0(X,\mathsf{S}^2T_X)$
. Up to the permuting of the coordinates, it suffices to prove that
![]() $s_0$
and
$s_0$
and
![]() $s_1$
are linearly independent. But
$s_1$
are linearly independent. But
![]() $h^2:H^0(X,\mathsf{S}^2T_X)\rightarrow H^0(R,\mathsf{S}^2T_R)$
maps
$h^2:H^0(X,\mathsf{S}^2T_X)\rightarrow H^0(R,\mathsf{S}^2T_R)$
maps
![]() $s_0$
to zero and maps
$s_0$
to zero and maps
![]() $s_i$
(for
$s_i$
(for
![]() $i\gt 0$
) to the corresponding elements
$i\gt 0$
) to the corresponding elements
![]() $\hat{s}_i$
of
$\hat{s}_i$
of
![]() $H^0(R,\mathsf{S}^2T_R)$
; this implies our assertion.
$H^0(R,\mathsf{S}^2T_R)$
; this implies our assertion.
Assume
![]() $n\geq 3$
. By the induction hypothesis, the homomorphism
$n\geq 3$
. By the induction hypothesis, the homomorphism
![]() $\mathbb{C}[t_1,\ldots, t_{n-1}]\rightarrow S(R)$
, which maps
$\mathbb{C}[t_1,\ldots, t_{n-1}]\rightarrow S(R)$
, which maps
![]() $t_i$
to
$t_i$
to
![]() $\hat{s_i}$
, is an isomorphism of graded
$\hat{s_i}$
, is an isomorphism of graded
![]() $\mathbb{C}$
-algebras (with
$\mathbb{C}$
-algebras (with
![]() $\deg (t_i)=2$
). It follows that
$\deg (t_i)=2$
). It follows that
![]() $h$
is surjective and that
$h$
is surjective and that
![]() $(s_0,\ldots, s_{n-1})$
form a basis of
$(s_0,\ldots, s_{n-1})$
form a basis of
![]() $H^0(X,\mathsf{S}^2 T_X)$
and generate the
$H^0(X,\mathsf{S}^2 T_X)$
and generate the
![]() $\mathbb{C}$
-algebra
$\mathbb{C}$
-algebra
![]() $S(X)$
. Thus we have a surjective homomorphism
$S(X)$
. Thus we have a surjective homomorphism
![]() $u:\mathbb{C}[t_0,\ldots, t_{n-1}]\rightarrow S(X)$
, with
$u:\mathbb{C}[t_0,\ldots, t_{n-1}]\rightarrow S(X)$
, with
![]() $u(t_i)=s_i$
.
$u(t_i)=s_i$
.
In particular, the Krull dimension of
![]() $S(X)$
is at most
$S(X)$
is at most
![]() $n$
. On the other hand, the ring
$n$
. On the other hand, the ring
![]() $S(X)$
is a domain, and
$S(X)$
is a domain, and
![]() $s_0$
is neither zero nor a unit. Thus, by Krull’s Hauptidealsatz, the Krull dimension of
$s_0$
is neither zero nor a unit. Thus, by Krull’s Hauptidealsatz, the Krull dimension of
![]() $S(X)$
is equal to
$S(X)$
is equal to
![]() $n$
; hence,
$n$
; hence,
![]() $u$
is an isomorphism. By permutation of the coordinates, we get the same result for any choice of
$u$
is an isomorphism. By permutation of the coordinates, we get the same result for any choice of
![]() $n$
elements in
$n$
elements in
![]() $\{s_0,\ldots, s_{n+2}\}$
. This proves the proposition.
$\{s_0,\ldots, s_{n+2}\}$
. This proves the proposition.
Conflicts of Interest
None.
Financial Support
J. Liu is supported by the National Key Research and Development Program of China (No. 2021YFA1002300), the NSFC grants (No. 12001521 and No. 12288201) and the CAS Project for Young Scientists in Basic Research (No. YSBR-033).
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.