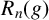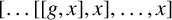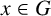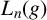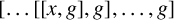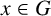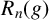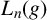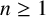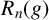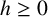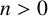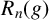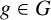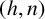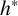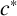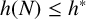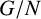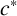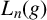1 Introduction
A group G is called an Engel group if for every
![]() $x,y\in G$
, the equation
$x,y\in G$
, the equation
![]() $[y,x,x,\ldots ,x]=1$
holds, where x is repeated in the commutator sufficiently many times depending on x and y. Throughout the paper, we use the left-normed simple commutator notation
$[y,x,x,\ldots ,x]=1$
holds, where x is repeated in the commutator sufficiently many times depending on x and y. Throughout the paper, we use the left-normed simple commutator notation
![]() $[a_1,a_2,a_3,\ldots ,a_r]=[\ldots [[a_1,a_2],a_3],\ldots ,a_r]$
. The long commutators
$[a_1,a_2,a_3,\ldots ,a_r]=[\ldots [[a_1,a_2],a_3],\ldots ,a_r]$
. The long commutators
![]() $[y,x,\ldots ,x]$
, where x occurs
$[y,x,\ldots ,x]$
, where x occurs
![]() $i\geq 0$
times, are denoted by
$i\geq 0$
times, are denoted by
![]() $[y,{}_i\,x]$
with
$[y,{}_i\,x]$
with
![]() $[y,{}_0\,x]=y$
. An element
$[y,{}_0\,x]=y$
. An element
![]() $g\in G$
is called a left Engel element if for each
$g\in G$
is called a left Engel element if for each
![]() $x\in G$
, there is a positive integer
$x\in G$
, there is a positive integer
![]() $n=n(g,x)$
such that
$n=n(g,x)$
such that
![]() $[x,{}_n\,g]=1$
. If n can be chosen independently of x, then g is a left n-Engel element of G. If
$[x,{}_n\,g]=1$
. If n can be chosen independently of x, then g is a left n-Engel element of G. If
![]() $g\in G$
and for all
$g\in G$
and for all
![]() $x\in G$
there exists a positive integer
$x\in G$
there exists a positive integer
![]() $n=n(g,x)$
such that
$n=n(g,x)$
such that
![]() $[g,{}_n\,x]=1$
, then g is a right Engel element of G. If n can be chosen independently of x, then g is a right n-Engel element of G. A group G is n-Engel if
$[g,{}_n\,x]=1$
, then g is a right Engel element of G. If n can be chosen independently of x, then g is a right n-Engel element of G. A group G is n-Engel if
![]() $[x,{}_n\,g]=1$
for all
$[x,{}_n\,g]=1$
for all
![]() $x,g\in G$
.
$x,g\in G$
.
Given
![]() $g\in G$
, write
$g\in G$
, write
![]() $R_n(g)$
for the subgroup generated by all commutators
$R_n(g)$
for the subgroup generated by all commutators
![]() $[g,{}_n\,x]$
, where x ranges over G. Similarly,
$[g,{}_n\,x]$
, where x ranges over G. Similarly,
![]() $L_n(g)$
stands for the subgroup generated by all commutators of the form
$L_n(g)$
stands for the subgroup generated by all commutators of the form
![]() $[x,{}_n\,g]$
.
$[x,{}_n\,g]$
.
There are several recent results showing that certain properties of groups with small subgroups
![]() $R_n(g)$
or
$R_n(g)$
or
![]() $L_n(g)$
are close to those of Engel groups (see for instance [Reference Khukhro and Shumyatsky3–Reference Khukhro and Shumyatsky5, Reference Shumyatsky8, Reference Shumyatsky9]). The present article deals with orderable groups. A group G is called orderable if there exists a full order relation
$L_n(g)$
are close to those of Engel groups (see for instance [Reference Khukhro and Shumyatsky3–Reference Khukhro and Shumyatsky5, Reference Shumyatsky8, Reference Shumyatsky9]). The present article deals with orderable groups. A group G is called orderable if there exists a full order relation
![]() $\leq $
on the set G such that
$\leq $
on the set G such that
![]() $x\leq y$
implies
$x\leq y$
implies
![]() $axb\leq ayb$
for all
$axb\leq ayb$
for all
![]() $a,b,x,y\in G$
, that is, the order on G is compatible with the product of G. Kim and Rhemtulla proved that any orderable n-Engel group is nilpotent ([Reference Kim, Rhemtulla, Kim and Johnson6], see also [Reference Longobardi and Maj7]). More recently, orderable groups with n-Engel word-values were considered [Reference Shumyatsky, Tortora and Tota10]. In the present article, we consider orderable groups G such that the subgroup
$a,b,x,y\in G$
, that is, the order on G is compatible with the product of G. Kim and Rhemtulla proved that any orderable n-Engel group is nilpotent ([Reference Kim, Rhemtulla, Kim and Johnson6], see also [Reference Longobardi and Maj7]). More recently, orderable groups with n-Engel word-values were considered [Reference Shumyatsky, Tortora and Tota10]. In the present article, we consider orderable groups G such that the subgroup
![]() $R_n(g)$
is polycyclic for each
$R_n(g)$
is polycyclic for each
![]() $g\in G$
. Recall that a group is polycyclic if and only if it admits a finite subnormal series all of whose factors are cyclic. The Hirsch length
$g\in G$
. Recall that a group is polycyclic if and only if it admits a finite subnormal series all of whose factors are cyclic. The Hirsch length
![]() $h(K)$
of a polycyclic group K is the number of infinite factors in the subnormal series. It is well known that every finitely generated nilpotent group is polycyclic.
$h(K)$
of a polycyclic group K is the number of infinite factors in the subnormal series. It is well known that every finitely generated nilpotent group is polycyclic.
Our aim here is to prove the following theorem.
Theorem 1.1. Let
![]() $h,n$
be positive integers and G be an orderable group in which
$h,n$
be positive integers and G be an orderable group in which
![]() $R_n(g)$
is polycyclic with
$R_n(g)$
is polycyclic with
![]() $h(R_n(g))\leq h$
for every
$h(R_n(g))\leq h$
for every
![]() $g\in G$
. Then, there exist
$g\in G$
. Then, there exist
![]() $(h,n)$
-bounded numbers
$(h,n)$
-bounded numbers
![]() $h^*$
and
$h^*$
and
![]() $c^*$
such that G has a finitely generated normal nilpotent subgroup N with
$c^*$
such that G has a finitely generated normal nilpotent subgroup N with
![]() $h(N)\leq h^*$
and
$h(N)\leq h^*$
and
![]() $G/N$
nilpotent of class at most
$G/N$
nilpotent of class at most
![]() $c^*$
.
$c^*$
.
A similar result for
![]() $L_n(g)$
was proved in [Reference Shumyatsky9]. We remark that while it is well known that the inverse of a right Engel element is left Engel, there is no such straightforward connection between the subgroups
$L_n(g)$
was proved in [Reference Shumyatsky9]. We remark that while it is well known that the inverse of a right Engel element is left Engel, there is no such straightforward connection between the subgroups
![]() $R_n(g)$
and
$R_n(g)$
and
![]() $L_n(g^{-1})$
, and our Theorem 1.1 is not a direct consequence of the result in [Reference Shumyatsky9].
$L_n(g^{-1})$
, and our Theorem 1.1 is not a direct consequence of the result in [Reference Shumyatsky9].
2 Preliminaries
We write
![]() $\langle X\rangle $
for a subgroup generated by a set X and
$\langle X\rangle $
for a subgroup generated by a set X and
![]() $\gamma _i(G)$
for the ith term of the lower central series of a group G.
$\gamma _i(G)$
for the ith term of the lower central series of a group G.
The following lemma plays a central role in what follows.
Lemma 2.1. Let a group G be a product of a normal abelian subgroup A by a cyclic subgroup
![]() $\langle g\rangle $
. Then,
$\langle g\rangle $
. Then,
![]() $L_{n+1}(g)\leq R_n(g^{-1})$
for any
$L_{n+1}(g)\leq R_n(g^{-1})$
for any
![]() $n\geq 1$
. In particular,
$n\geq 1$
. In particular,
![]() $ \gamma _{n+1}(G)\leq R_{n-1}(g^{-1})$
for any
$ \gamma _{n+1}(G)\leq R_{n-1}(g^{-1})$
for any
![]() $n\geq 2$
.
$n\geq 2$
.
Proof. Let
![]() $x\in G$
and write
$x\in G$
and write
![]() $x=yg^i$
, where
$x=yg^i$
, where
![]() $y\in A$
. An easy induction on n shows that
$y\in A$
. An easy induction on n shows that
![]() $[yg^i,{}_{n+1}\,g]= [y,{}_{n+1}\,g]^{g^i}[g^i,{}_{n+1}\,g]$
. We have
$[yg^i,{}_{n+1}\,g]= [y,{}_{n+1}\,g]^{g^i}[g^i,{}_{n+1}\,g]$
. We have
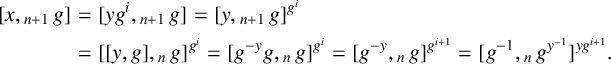 $$ \begin{align*} [x,{}_{n+1}\,g] & = [yg^i,{}_{n+1}\,g]= [y,{}_{n+1}\,g]^{g^i} \\ &= [[y,g],{}_{n}\,g]^{g^i}= [g^{-y}g,{}_{n}\,g]^{g^i}= [g^{-y},{}_n\,g]^{g^{i+1}}= [g^{-1},{}_n\,g^{y^{-1}}]^{yg^{i+1}}. \end{align*} $$
$$ \begin{align*} [x,{}_{n+1}\,g] & = [yg^i,{}_{n+1}\,g]= [y,{}_{n+1}\,g]^{g^i} \\ &= [[y,g],{}_{n}\,g]^{g^i}= [g^{-y}g,{}_{n}\,g]^{g^i}= [g^{-y},{}_n\,g]^{g^{i+1}}= [g^{-1},{}_n\,g^{y^{-1}}]^{yg^{i+1}}. \end{align*} $$
Since
![]() $G'$
is contained in A and A is abelian, it follows that
$G'$
is contained in A and A is abelian, it follows that
Hence,
![]() $L_{n+1}(g)\leq R_{n}(g^{-1})$
.
$L_{n+1}(g)\leq R_{n}(g^{-1})$
.
We obviously have
![]() $\gamma _{n+1}(G)\leq L_n(g)$
and so it follows that
$\gamma _{n+1}(G)\leq L_n(g)$
and so it follows that
![]() $\gamma _{n+1}(G)\leq R_{n-1}(g^{-1})$
for any
$\gamma _{n+1}(G)\leq R_{n-1}(g^{-1})$
for any
![]() $n\geq 2$
.
$n\geq 2$
.
Certainly, under the hypotheses of Lemma 2.1, we have
![]() $\gamma _{n+1}(G)\leq R_{n-1}(g)$
.
$\gamma _{n+1}(G)\leq R_{n-1}(g)$
.
Lemma 2.2 [Reference Shumyatsky9, Lemma 2.1].
Let
![]() $G=H\langle g\rangle $
, where H is a nilpotent of class c normal subgroup and g is a left n-Engel element. Then, G is nilpotent with class at most
$G=H\langle g\rangle $
, where H is a nilpotent of class c normal subgroup and g is a left n-Engel element. Then, G is nilpotent with class at most
![]() $cn$
.
$cn$
.
Lemma 2.3. Let
![]() $G=H\langle g\rangle $
, where H is a nilpotent of class c normal subgroup. For any positive integers
$G=H\langle g\rangle $
, where H is a nilpotent of class c normal subgroup. For any positive integers
![]() $c,n$
, there exists an integer
$c,n$
, there exists an integer
![]() $f=f(c,n)$
such that
$f=f(c,n)$
such that
![]() $\gamma _f(G)\leq R_n(g)$
.
$\gamma _f(G)\leq R_n(g)$
.
Proof. We argue by induction on c. If H is abelian, then Lemma 2.1 gives
![]() ${\gamma _{n+2}(G)\leq R_{n}(g)}$
and so it is enough to choose
${\gamma _{n+2}(G)\leq R_{n}(g)}$
and so it is enough to choose
![]() $f=n+2$
. Assume that
$f=n+2$
. Assume that
![]() $c\geq 2$
and let
$c\geq 2$
and let
![]() $Z=Z(H)$
. By induction, there exists a bounded number s such that
$Z=Z(H)$
. By induction, there exists a bounded number s such that
![]() $\gamma _s(G)\leq ZR_n(g)$
. Let
$\gamma _s(G)\leq ZR_n(g)$
. Let
![]() $R= R_n(g)\cap Z\gamma _s(G)$
and hence
$R= R_n(g)\cap Z\gamma _s(G)$
and hence
![]() $\gamma _s(G)\leq ZR$
. Arguing modulo Z, we have
$\gamma _s(G)\leq ZR$
. Arguing modulo Z, we have
![]() $ZR=Z(R_n(g)\cap Z\gamma _s(G))= Z\gamma _s(G)$
. So
$ZR=Z(R_n(g)\cap Z\gamma _s(G))= Z\gamma _s(G)$
. So
![]() $ZR$
is normal in G. Set
$ZR$
is normal in G. Set
![]() $Z_0=ZR$
and, for
$Z_0=ZR$
and, for
![]() $i=0,1,\ldots ,s-1$
, let
$i=0,1,\ldots ,s-1$
, let
![]() $Z_i$
denote the full inverse image of
$Z_i$
denote the full inverse image of
![]() $Z_i(G/Z_0)$
. Further, for
$Z_i(G/Z_0)$
. Further, for
![]() $i=0,1,\ldots ,s-1$
, we set
$i=0,1,\ldots ,s-1$
, we set
![]() $G_i=Z_i\langle g\rangle $
. It is clear that
$G_i=Z_i\langle g\rangle $
. It is clear that
![]() $G/Z_0$
is nilpotent and
$G/Z_0$
is nilpotent and
![]() $Z_{s-1}=G_{s-1}=G$
.
$Z_{s-1}=G_{s-1}=G$
.
Since Z is abelian, Lemma 2.1 gives
![]() $[Z,{}_{n+1}\,g^{-1}]\leq R_n(g)\cap Z\leq R$
. We observe that Z and R are commuting g-invariant subgroups and so
$[Z,{}_{n+1}\,g^{-1}]\leq R_n(g)\cap Z\leq R$
. We observe that Z and R are commuting g-invariant subgroups and so
![]() $[Z_0,{}_{n+1}\,g^{-1}]=[Z,{}_{n+1}\,g^{-1}][R,{}_{n+1}\,g^{-1}]\leq R$
. Let T be the normal closure of
$[Z_0,{}_{n+1}\,g^{-1}]=[Z,{}_{n+1}\,g^{-1}][R,{}_{n+1}\,g^{-1}]\leq R$
. Let T be the normal closure of
![]() $[Z_0,{}_{n+1}\,g^{-1}]$
in
$[Z_0,{}_{n+1}\,g^{-1}]$
in
![]() $G_0$
. Note that
$G_0$
. Note that
![]() $R\leq G'\leq H$
. Hence,
$R\leq G'\leq H$
. Hence,
![]() $ZR\leq H$
and since R is g-invariant, we have
$ZR\leq H$
and since R is g-invariant, we have
![]() $T\leq R$
. As the image of
$T\leq R$
. As the image of
![]() $g^{-1}$
in
$g^{-1}$
in
![]() $G_0/T$
is left
$G_0/T$
is left
![]() $(n+1)$
-Engel and
$(n+1)$
-Engel and
![]() $ZR/T$
is nilpotent, Lemma 2.2 implies that there exists a bounded number k such that
$ZR/T$
is nilpotent, Lemma 2.2 implies that there exists a bounded number k such that
![]() $G_0/T$
is nilpotent with class at most
$G_0/T$
is nilpotent with class at most
![]() $k-1$
and so
$k-1$
and so
![]() $\gamma _k(G_0)\leq R$
.
$\gamma _k(G_0)\leq R$
.
By induction on i, we will show that there exists a bounded number
![]() $k_i$
such that
$k_i$
such that
![]() $\gamma _{k_i}(G_i)\leq R$
. Once this is done, we will simply set
$\gamma _{k_i}(G_i)\leq R$
. Once this is done, we will simply set
![]() $f=k_{s-1}$
. Assume that for some
$f=k_{s-1}$
. Assume that for some
![]() $j\leq s-1$
, there exists
$j\leq s-1$
, there exists
![]() $k_j$
with the property that
$k_j$
with the property that
![]() $\gamma _{k_j}(G_j)\leq R$
. If
$\gamma _{k_j}(G_j)\leq R$
. If
![]() $j=s-1$
, we have nothing to prove, so we suppose that
$j=s-1$
, we have nothing to prove, so we suppose that
![]() $j\leq s-2$
. Since
$j\leq s-2$
. Since
![]() $G_{j+1}$
normalises
$G_{j+1}$
normalises
![]() $G_j$
, it follows that
$G_j$
, it follows that
![]() $\gamma _{k_j}(G_j)$
is normal in
$\gamma _{k_j}(G_j)$
is normal in
![]() $G_{j+1}$
. Recall that
$G_{j+1}$
. Recall that
![]() $\gamma _s(G)\leq G_0$
. Then, if
$\gamma _s(G)\leq G_0$
. Then, if
![]() $x\in G_{j+1}$
, we get
$x\in G_{j+1}$
, we get
![]() $[x,{}_{s-1}\,g]\in \gamma _s(G)$
and hence
$[x,{}_{s-1}\,g]\in \gamma _s(G)$
and hence
![]() $[x,{}_{s+k_j-2}\,g]\in \gamma _{k_j}(G_j)$
. It follows that the image of g in
$[x,{}_{s+k_j-2}\,g]\in \gamma _{k_j}(G_j)$
. It follows that the image of g in
![]() $G_{j+1}/\gamma _{k_j}(G_j)$
is left
$G_{j+1}/\gamma _{k_j}(G_j)$
is left
![]() $(s+k_j-2)$
-Engel. Applying Lemma 2.2 to the factor-group
$(s+k_j-2)$
-Engel. Applying Lemma 2.2 to the factor-group
![]() $G_{j+1}/\gamma _{k_j}(G_j)=((G_{j+1}\cap H)\gamma _{k_j}(G_j)/\gamma _{k_j}(G_j))\langle g\gamma _{k_j}(G_j)\rangle $
, we see that it is nilpotent with bounded class, say
$G_{j+1}/\gamma _{k_j}(G_j)=((G_{j+1}\cap H)\gamma _{k_j}(G_j)/\gamma _{k_j}(G_j))\langle g\gamma _{k_j}(G_j)\rangle $
, we see that it is nilpotent with bounded class, say
![]() ${k_{j+1}-1}$
. We conclude that
${k_{j+1}-1}$
. We conclude that
![]() $\gamma _{k_{j+1}}(G_{j+1})\leq R$
. This completes the proof.
$\gamma _{k_{j+1}}(G_{j+1})\leq R$
. This completes the proof.
Given subgroups
![]() $ X$
and Y of a group G, we denote by
$ X$
and Y of a group G, we denote by
![]() $X^Y$
the smallest subgroup of G containing X and normalised by Y. We say that a group G satisfies
$X^Y$
the smallest subgroup of G containing X and normalised by Y. We say that a group G satisfies
![]() $\max $
if G satisfies the maximal condition on subgroups.
$\max $
if G satisfies the maximal condition on subgroups.
Lemma 2.4. Let g and y be elements of a group G, and suppose that for some
![]() $n\geq 1$
, the subgroup
$n\geq 1$
, the subgroup
![]() $R_n(g)$
satisfies
$R_n(g)$
satisfies
![]() $\max $
. Then,
$\max $
. Then,
![]() $\langle g\rangle ^{\langle y\rangle }$
is finitely generated.
$\langle g\rangle ^{\langle y\rangle }$
is finitely generated.
Proof. Observe that
![]() $\langle g\rangle ^{\langle y\rangle }$
is generated by all commutators
$\langle g\rangle ^{\langle y\rangle }$
is generated by all commutators
![]() $[g,{}_{i}\,y]$
for
$[g,{}_{i}\,y]$
for
![]() $i\geq 0$
. Set
$i\geq 0$
. Set
![]() ${Y =\langle g\rangle ^{\langle y\rangle }\cap R_n(g)}$
. We have
${Y =\langle g\rangle ^{\langle y\rangle }\cap R_n(g)}$
. We have
![]() $ \langle g\rangle ^{\langle y\rangle } = \langle g,[g,y],\ldots ,[g,{}_{n-1}\,y],Y\rangle $
. Since
$ \langle g\rangle ^{\langle y\rangle } = \langle g,[g,y],\ldots ,[g,{}_{n-1}\,y],Y\rangle $
. Since
![]() $R_n(g)$
satisfies
$R_n(g)$
satisfies
![]() $\max $
, Y is finitely generated and so the lemma follows.
$\max $
, Y is finitely generated and so the lemma follows.
Corollary 2.5. Let
![]() $g_1,\ldots ,g_m$
be elements of a group G such that for some
$g_1,\ldots ,g_m$
be elements of a group G such that for some
![]() $n\geq 1$
, the subgroups
$n\geq 1$
, the subgroups
![]() $R_n(g_i)$
satisfy
$R_n(g_i)$
satisfy
![]() $\max $
for every
$\max $
for every
![]() $i\in \{1,\ldots ,m\}$
. If
$i\in \{1,\ldots ,m\}$
. If
![]() $y\in G$
, then
$y\in G$
, then
![]() $\langle g_1,\ldots ,g_m\rangle ^{\langle y\rangle }$
is finitely generated.
$\langle g_1,\ldots ,g_m\rangle ^{\langle y\rangle }$
is finitely generated.
Lemma 2.6 [Reference Shumyatsky9, Lemma 2.8].
If G is a group generated by two elements x and y, then
![]() $G'=\langle [x,y]^{x^ry^s} \mid r,s\in \mathbb Z\rangle $
.
$G'=\langle [x,y]^{x^ry^s} \mid r,s\in \mathbb Z\rangle $
.
Using the previous results, we are able to prove the following lemma.
Lemma 2.7. Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $G=\langle g_1,\ldots ,g_m\rangle $
such that
$G=\langle g_1,\ldots ,g_m\rangle $
such that
![]() $R_n([g_i,g_j])$
satisfies
$R_n([g_i,g_j])$
satisfies
![]() $\max $
for all
$\max $
for all
![]() $i,j\in \{1,\ldots , m\}$
. Then,
$i,j\in \{1,\ldots , m\}$
. Then,
![]() $G'$
is finitely generated.
$G'$
is finitely generated.
Proof. First, assume that
![]() $m=2$
. Then,
$m=2$
. Then,
![]() $G'=\langle [g_1,g_2]^{g_1^rg_2^s} \mid r,s\in \mathbb Z\rangle $
by Lemma 2.6. However, by repeated applications of Corollary 2.5,
$G'=\langle [g_1,g_2]^{g_1^rg_2^s} \mid r,s\in \mathbb Z\rangle $
by Lemma 2.6. However, by repeated applications of Corollary 2.5,
![]() $(\langle [g_1,g_2]\rangle ^{\langle g_1\rangle })^{\langle g_2\rangle }$
is finitely generated. Now, suppose that
$(\langle [g_1,g_2]\rangle ^{\langle g_1\rangle })^{\langle g_2\rangle }$
is finitely generated. Now, suppose that
![]() $m \geq 3$
, and assume that the result is true for subgroups which can be generated by at most
$m \geq 3$
, and assume that the result is true for subgroups which can be generated by at most
![]() $m-1$
elements from
$m-1$
elements from
![]() $\{g_1,\ldots ,g_m\}$
. For
$\{g_1,\ldots ,g_m\}$
. For
![]() $i=1,\ldots ,m$
, set
$i=1,\ldots ,m$
, set
![]() $G_i=\langle g_1,\ldots ,g_{i-1},g_{i+1},\ldots ,g_m\rangle $
. By the induction hypothesis,
$G_i=\langle g_1,\ldots ,g_{i-1},g_{i+1},\ldots ,g_m\rangle $
. By the induction hypothesis,
![]() $G_i^{\prime }$
is finitely generated and, by Corollary 2.5, the same is true for
$G_i^{\prime }$
is finitely generated and, by Corollary 2.5, the same is true for
![]() $(G_i^{\prime })^{\langle g_i\rangle }$
. Moreover, it is easy to see that
$(G_i^{\prime })^{\langle g_i\rangle }$
. Moreover, it is easy to see that
![]() $ K=\langle (G_i^{\prime })^{\langle g_i\rangle } \mid i = 1,\ldots , m\rangle $
is a normal subgroup of G and hence
$ K=\langle (G_i^{\prime })^{\langle g_i\rangle } \mid i = 1,\ldots , m\rangle $
is a normal subgroup of G and hence
![]() $G'= K$
. In particular,
$G'= K$
. In particular,
![]() $G'$
is finitely generated.
$G'$
is finitely generated.
Now, an easy induction yields the following corollary.
Corollary 2.8. Let G be a finitely generated group such that for each
![]() $g\in G$
, there exists
$g\in G$
, there exists
![]() $n\geq 1$
with the property that
$n\geq 1$
with the property that
![]() $R_n(g)$
satisfies
$R_n(g)$
satisfies
![]() $\max $
. Then, each term of the derived series of G is finitely generated.
$\max $
. Then, each term of the derived series of G is finitely generated.
Lemma 2.9 [Reference Shumyatsky9, Corollary 2.5].
Let
![]() $G=H\langle g\rangle $
be a nilpotent group with a normal torsion-free subgroup H of Hirsch length h. Then, G is nilpotent with h-bounded class.
$G=H\langle g\rangle $
be a nilpotent group with a normal torsion-free subgroup H of Hirsch length h. Then, G is nilpotent with h-bounded class.
3 Proof of Theorem 1.1
It is easy to see that any orderable group is torsion-free. The class of orderable groups is closed under taking subgroups, but a quotient of an orderable group is not necessarily orderable [Reference Botto Mura and Rhemtulla1, Section 2.1]. A subgroup C of an ordered group
![]() $(G,\leq )$
is called convex if
$(G,\leq )$
is called convex if
![]() $x\in C$
whenever
$x\in C$
whenever
![]() $1\leq x \leq c$
for some
$1\leq x \leq c$
for some
![]() $c\in C$
. Obviously,
$c\in C$
. Obviously,
![]() $\{1\}$
and G are convex subgroups of G; and, if C is a convex subgroup, then every conjugate of C is convex. If C is a normal convex subgroup of an ordered group G, then
$\{1\}$
and G are convex subgroups of G; and, if C is a convex subgroup, then every conjugate of C is convex. If C is a normal convex subgroup of an ordered group G, then
![]() $G/C$
is ordered [Reference Botto Mura and Rhemtulla1, Section 2.1]. It is also clear that all convex subgroups of an ordered group form, by inclusion, a totally ordered set, which is closed under intersection and union. If C and D are convex subgroups of an ordered group G, with
$G/C$
is ordered [Reference Botto Mura and Rhemtulla1, Section 2.1]. It is also clear that all convex subgroups of an ordered group form, by inclusion, a totally ordered set, which is closed under intersection and union. If C and D are convex subgroups of an ordered group G, with
![]() $C< D$
, and there is not a convex subgroup H of G such that
$C< D$
, and there is not a convex subgroup H of G such that
![]() $C< H < D$
, we say that the pair
$C< H < D$
, we say that the pair
![]() $(C, D)$
is a convex jump in G. Orders on a group G in which
$(C, D)$
is a convex jump in G. Orders on a group G in which
![]() $\{1\}$
and G are the only convex subgroups are very well known. By a result of Hölder [Reference Botto Mura and Rhemtulla1, Theorem 1.3.4], a group G with such an order is order-isomorphic to a subgroup of the additive group of the real numbers under the natural order. This implies that if
$\{1\}$
and G are the only convex subgroups are very well known. By a result of Hölder [Reference Botto Mura and Rhemtulla1, Theorem 1.3.4], a group G with such an order is order-isomorphic to a subgroup of the additive group of the real numbers under the natural order. This implies that if
![]() $(C, D)$
is a convex jump of an ordered group, then C is normal in D and
$(C, D)$
is a convex jump of an ordered group, then C is normal in D and
![]() $D/C$
is abelian [Reference Botto Mura and Rhemtulla1, Lemma 1.3.6].
$D/C$
is abelian [Reference Botto Mura and Rhemtulla1, Lemma 1.3.6].
The following lemma is an application of Lemma 2.4.
Lemma 3.1. Let G be an orderable group in which for each g, there exists
![]() $n\geq 1$
such that
$n\geq 1$
such that
![]() $R_n(g)$
satisfies
$R_n(g)$
satisfies
![]() $\max $
. Then, each convex subgroup in G is normal.
$\max $
. Then, each convex subgroup in G is normal.
Proof. Suppose that C is convex and not normal in G. Then, there exists
![]() $x\in G$
such that
$x\in G$
such that
![]() $C\neq C^x$
. Since convex subgroups form a chain, we have either
$C\neq C^x$
. Since convex subgroups form a chain, we have either
![]() $C^x <C$
or
$C^x <C$
or
![]() $C<C^x$
. Without loss of generality, assume that
$C<C^x$
. Without loss of generality, assume that
![]() $C<C^x$
and let
$C<C^x$
and let
![]() $c^x \in C^x\setminus C$
for a suitable
$c^x \in C^x\setminus C$
for a suitable
![]() $c\in C$
. Then,
$c\in C$
. Then,
![]() $C^{x^i} < C^{x^{i+1}}$
for any integer i. Moreover, by Lemma 2.4, the subgroup
$C^{x^i} < C^{x^{i+1}}$
for any integer i. Moreover, by Lemma 2.4, the subgroup
![]() $\langle c\rangle ^{\langle x \rangle }$
is finitely generated so that
$\langle c\rangle ^{\langle x \rangle }$
is finitely generated so that
![]() $\langle c\rangle ^{\langle x \rangle }=\langle c^{x^{i_1}}, \ldots , c^{x^{i_k}} \rangle $
, where
$\langle c\rangle ^{\langle x \rangle }=\langle c^{x^{i_1}}, \ldots , c^{x^{i_k}} \rangle $
, where
![]() $i_1,\ldots , i_k$
are integers. We may assume
$i_1,\ldots , i_k$
are integers. We may assume
![]() $i_1 <i_2 < \cdots < i_k$
. It follows that
$i_1 <i_2 < \cdots < i_k$
. It follows that
![]() $\langle c\rangle ^{\langle x \rangle } \leq C^{x^{i_k}}$
. Hence,
$\langle c\rangle ^{\langle x \rangle } \leq C^{x^{i_k}}$
. Hence,
![]() $c^{x^{i_k+1}} \in C^{x^{i_k}}$
and therefore
$c^{x^{i_k+1}} \in C^{x^{i_k}}$
and therefore
![]() $c^x \in C$
, which is a contradiction.
$c^x \in C$
, which is a contradiction.
We will need the following result due to Zelmanov [Reference Zelmanov11] (see also [Reference Burns and Medvedev2]).
Theorem 3.2. Let
![]() $n\geq 1$
and G be a nilpotent torsion-free n-Engel group. Then, G is nilpotent of n-bounded nilpotency class.
$n\geq 1$
and G be a nilpotent torsion-free n-Engel group. Then, G is nilpotent of n-bounded nilpotency class.
Lemma 3.3. Let
![]() $h,n$
be positive integers and G be an orderable group in which
$h,n$
be positive integers and G be an orderable group in which
![]() $R_n(g)$
is polycyclic with
$R_n(g)$
is polycyclic with
![]() $h(R_n(g))\leq h$
for every
$h(R_n(g))\leq h$
for every
![]() $g\in G$
. Then,
$g\in G$
. Then,
![]() $G'$
is nilpotent with
$G'$
is nilpotent with
![]() $(h,n)$
-bounded class.
$(h,n)$
-bounded class.
Proof. It is sufficient to establish the result under the additional hypothesis that G is finitely generated. Thus, assume that G is finitely generated. Since polycyclic groups satisfy
![]() $\max $
, we know by Lemma 3.1 that the convex subgroups in G are normal. Let C be a convex subgroup such that
$\max $
, we know by Lemma 3.1 that the convex subgroups in G are normal. Let C be a convex subgroup such that
![]() $G/C$
is soluble. By Corollary 2.8, all terms of the derived series of G are finitely generated. It follows that
$G/C$
is soluble. By Corollary 2.8, all terms of the derived series of G are finitely generated. It follows that
![]() $G/C$
has finite rank and therefore, by [Reference Botto Mura and Rhemtulla1, Theorem 3.3.1], the derived group
$G/C$
has finite rank and therefore, by [Reference Botto Mura and Rhemtulla1, Theorem 3.3.1], the derived group
![]() $(G/C)'$
is nilpotent. Hence, each element of
$(G/C)'$
is nilpotent. Hence, each element of
![]() $(G/C)'$
is left Engel. For
$(G/C)'$
is left Engel. For
![]() $x\in G/C$
and
$x\in G/C$
and
![]() $y\in (G/C)'$
, let
$y\in (G/C)'$
, let
![]() $J_{x,y}$
be the subgroup generated by all commutators
$J_{x,y}$
be the subgroup generated by all commutators
![]() $[x,{}_k\,y]$
, where
$[x,{}_k\,y]$
, where
![]() $k\geq n$
. The subgroup
$k\geq n$
. The subgroup
![]() $J_{x,y}$
is a y-invariant nilpotent subgroup with
$J_{x,y}$
is a y-invariant nilpotent subgroup with
![]() $h(J_{x,y})\leq h$
.
$h(J_{x,y})\leq h$
.
In view of Lemma 2.9, the subgroup
![]() $J_{x,y}\langle y\rangle $
is nilpotent of h-bounded class. Therefore, there is an
$J_{x,y}\langle y\rangle $
is nilpotent of h-bounded class. Therefore, there is an
![]() $(h,n)$
-bounded number
$(h,n)$
-bounded number
![]() $n_0$
such that y is
$n_0$
such that y is
![]() $n_0$
-Engel in
$n_0$
-Engel in
![]() $G/C$
. Hence, every element of
$G/C$
. Hence, every element of
![]() $(G/C)'$
is left
$(G/C)'$
is left
![]() $n_0$
-Engel. Now, Theorem 3.2 tells us that
$n_0$
-Engel. Now, Theorem 3.2 tells us that
![]() $(G/C)'$
is nilpotent of
$(G/C)'$
is nilpotent of
![]() $(h,n)$
-bounded nilpotency class. In particular, we deduce that
$(h,n)$
-bounded nilpotency class. In particular, we deduce that
![]() $G/C$
has
$G/C$
has
![]() $(h,n)$
-bounded derived length, say d.
$(h,n)$
-bounded derived length, say d.
Let S be the intersection of all convex subgroups N of G such that
![]() $G/N$
is soluble. The above argument shows that
$G/N$
is soluble. The above argument shows that
![]() $G^{(d)}\leq S$
. Since all terms of the derived series of G are finitely generated, it follows that
$G^{(d)}\leq S$
. Since all terms of the derived series of G are finitely generated, it follows that
![]() $G/G^{(d)}$
satisfies
$G/G^{(d)}$
satisfies
![]() $\max $
and we conclude that S is finitely generated, too. Then, if
$\max $
and we conclude that S is finitely generated, too. Then, if
![]() $S\neq 1$
, among the convex subgroups properly contained in S, we can choose a maximal one, say D. It follows that
$S\neq 1$
, among the convex subgroups properly contained in S, we can choose a maximal one, say D. It follows that
![]() $(D,S)$
is a convex jump in G. Hence,
$(D,S)$
is a convex jump in G. Hence,
![]() $S/D$
is abelian and so
$S/D$
is abelian and so
![]() $G/D$
is soluble. This is a contradiction since S is the intersection of all convex subgroups N of G such that
$G/D$
is soluble. This is a contradiction since S is the intersection of all convex subgroups N of G such that
![]() $G/N$
is soluble. The conclusion is that
$G/N$
is soluble. The conclusion is that
![]() $S=1$
and G is soluble with derived length at most d. Again, we observe that G has finite rank whence, by [Reference Botto Mura and Rhemtulla1, Theorem 3.3.1],
$S=1$
and G is soluble with derived length at most d. Again, we observe that G has finite rank whence, by [Reference Botto Mura and Rhemtulla1, Theorem 3.3.1],
![]() $G'$
is nilpotent. Finally, arguing as above, every element of
$G'$
is nilpotent. Finally, arguing as above, every element of
![]() $G'$
is left
$G'$
is left
![]() $n_0$
-Engel. Hence, by Theorem 3.2, the nilpotency class of
$n_0$
-Engel. Hence, by Theorem 3.2, the nilpotency class of
![]() $G'$
is
$G'$
is
![]() $(h,n)$
-bounded.
$(h,n)$
-bounded.
We are now ready to complete the proof of Theorem 1.1, which we restate here for the reader’s convenience.
Theorem. Let
![]() $h,n$
be positive integers and G be an orderable group in which
$h,n$
be positive integers and G be an orderable group in which
![]() $R_n(g)$
is polycyclic with
$R_n(g)$
is polycyclic with
![]() $h(R_n(g))\leq h$
for every
$h(R_n(g))\leq h$
for every
![]() $g\in G$
. Then, there exist
$g\in G$
. Then, there exist
![]() $(h,n)$
-bounded numbers
$(h,n)$
-bounded numbers
![]() $h^*$
and
$h^*$
and
![]() $c^*$
such that G has a finitely generated normal nilpotent subgroup N with
$c^*$
such that G has a finitely generated normal nilpotent subgroup N with
![]() ${h(N)\leq h^*}$
and
${h(N)\leq h^*}$
and
![]() $G/N$
nilpotent of class at most
$G/N$
nilpotent of class at most
![]() $c^*$
.
$c^*$
.
Proof. For any
![]() $x\in G$
, set
$x\in G$
, set
![]() $H_x=G'\langle x\rangle $
. In view of Lemma 3.3,
$H_x=G'\langle x\rangle $
. In view of Lemma 3.3,
![]() $G'$
is nilpotent and Lemma 2.3 tells us that there is a bounded number f such that
$G'$
is nilpotent and Lemma 2.3 tells us that there is a bounded number f such that
![]() $\gamma _f(H_x)\leq R_n(x)$
. It follows that
$\gamma _f(H_x)\leq R_n(x)$
. It follows that
![]() $h(\gamma _f(H_x))\leq h$
and therefore
$h(\gamma _f(H_x))\leq h$
and therefore
![]() $h(L_{f-1}(x))\leq h$
. Hence, we can apply the main theorem from [Reference Shumyatsky9], which completes the proof.
$h(L_{f-1}(x))\leq h$
. Hence, we can apply the main theorem from [Reference Shumyatsky9], which completes the proof.
Acknowledgement
This work was done during a visit of the first and the second authors at the Department of Mathematics of the University of Salerno. They thank the department for their hospitality.