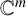1 Introduction
An analytic function f over a domain
![]() $\Omega \subseteq \mathbb {C}$
is said to be an algebraic function over
$\Omega \subseteq \mathbb {C}$
is said to be an algebraic function over
![]() $\mathbb {C}(z)$
if there exists a nonzero polynomial
$\mathbb {C}(z)$
if there exists a nonzero polynomial
![]() $P\in \mathbb {C}[X,Y]$
for which
$P\in \mathbb {C}[X,Y]$
for which
![]() $P(z,f(z))=0$
, for all
$P(z,f(z))=0$
, for all
![]() $z\in \Omega $
. A function which is not algebraic is called a transcendental function.
$z\in \Omega $
. A function which is not algebraic is called a transcendental function.
The study of the arithmetic behaviour of transcendental functions started in 1886 with a letter of Weierstrass to Strauss, proving the existence of such functions taking
![]() $\mathbb {Q}$
into itself. Weierstrass also conjectured the existence of a transcendental entire function f for which
$\mathbb {Q}$
into itself. Weierstrass also conjectured the existence of a transcendental entire function f for which
![]() $f(\overline {\mathbb {Q}})\subseteq \overline {\mathbb {Q}}$
(as usual,
$f(\overline {\mathbb {Q}})\subseteq \overline {\mathbb {Q}}$
(as usual,
![]() $\overline {\mathbb {Q}}$
denotes the field of all algebraic numbers). Motivated by results of this kind, he defined the exceptional set of an analytic function
$\overline {\mathbb {Q}}$
denotes the field of all algebraic numbers). Motivated by results of this kind, he defined the exceptional set of an analytic function
![]() $f:\Omega \to \mathbb {C}$
as
$f:\Omega \to \mathbb {C}$
as
Thus, Weierstrass’ conjecture can be rephrased as: does there exist a transcendental entire function f such that
![]() $S_f=\overline {\mathbb {Q}}$
? This conjecture was settled in 1895 by Stäckel [Reference Stäckel4], who proved, in particular, that for any
$S_f=\overline {\mathbb {Q}}$
? This conjecture was settled in 1895 by Stäckel [Reference Stäckel4], who proved, in particular, that for any
![]() $\Sigma \subseteq \overline {\mathbb {Q}}$
, there exists a transcendental entire function f for which
$\Sigma \subseteq \overline {\mathbb {Q}}$
, there exists a transcendental entire function f for which
![]() $\Sigma \subseteq S_f$
.
$\Sigma \subseteq S_f$
.
In his classical book [Reference Mahler1], Mahler introduced the problem of studying
![]() $S_f$
for various classes of functions. After discussing a number of examples, Mahler posed several problems about the admissible exceptional sets for analytic functions, one of which is as follows. Here
$S_f$
for various classes of functions. After discussing a number of examples, Mahler posed several problems about the admissible exceptional sets for analytic functions, one of which is as follows. Here
![]() $B(0,\rho )$
denotes the closed ball with centre 0 and radius
$B(0,\rho )$
denotes the closed ball with centre 0 and radius
![]() $\rho $
in
$\rho $
in
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Problem 1.1. Let
![]() $\rho \in (0,\infty ]$
be a real number. Does there exist for any choice of
$\rho \in (0,\infty ]$
be a real number. Does there exist for any choice of
![]() $S\subseteq \overline {\mathbb {Q}}\cap B(0,\rho )$
(closed under complex conjugation and such that
$S\subseteq \overline {\mathbb {Q}}\cap B(0,\rho )$
(closed under complex conjugation and such that
![]() $0\in S$
) a transcendental analytic function
$0\in S$
) a transcendental analytic function
![]() $f\in \mathbb {Q}[[z]]$
with radius of convergence
$f\in \mathbb {Q}[[z]]$
with radius of convergence
![]() $\rho $
for which
$\rho $
for which
![]() $S_f=S$
?
$S_f=S$
?
In 2016, Marques and Ramirez [Reference Marques and Ramirez3] proved that the answer to this question is ‘yes’ provided that
![]() $\rho =\infty $
(that is, for entire functions). Indeed, they proved the following more general result about the arithmetic behaviour of certain entire functions.
$\rho =\infty $
(that is, for entire functions). Indeed, they proved the following more general result about the arithmetic behaviour of certain entire functions.
Lemma 1.2 [Reference Marques and Ramirez3, Theorem 1.3].
Let A be a countable set and let
![]() $\mathbb {K}$
be a dense subset of
$\mathbb {K}$
be a dense subset of
![]() $\mathbb {C}$
. For each
$\mathbb {C}$
. For each
![]() $\alpha \in A$
, fix a dense subset
$\alpha \in A$
, fix a dense subset
![]() $E_{\alpha }\subseteq \mathbb {C}$
. Then there exist uncountably many transcendental entire functions
$E_{\alpha }\subseteq \mathbb {C}$
. Then there exist uncountably many transcendental entire functions
![]() $f\in \mathbb {K}[[z]]$
such that
$f\in \mathbb {K}[[z]]$
such that
![]() $f(\alpha )\in E_{\alpha }$
for all
$f(\alpha )\in E_{\alpha }$
for all
![]() $\alpha \in A$
.
$\alpha \in A$
.
This result was improved by Marques and Moreira in [Reference Marques and Moreira2] giving an affirmative answer to Mahler’s Problem 1.1 for any
![]() $\rho \in (0,\infty ]$
.
$\rho \in (0,\infty ]$
.
In this paper, we consider Mahler’s Problem 1.1 in the context of transcendental entire functions of several variables. Although the previous definitions extend to the context of several variables in a very natural way, we shall include them here for the sake of completeness.
An analytic function f over a domain
![]() $\Omega \subseteq \mathbb {C}^m$
(we also say that f is entire if
$\Omega \subseteq \mathbb {C}^m$
(we also say that f is entire if
![]() $\Omega =\mathbb {C}^m$
) is said to be algebraic over
$\Omega =\mathbb {C}^m$
) is said to be algebraic over
![]() $\mathbb {C}(z_1,\ldots ,z_m)$
if it is a solution of a polynomial functional equation
$\mathbb {C}(z_1,\ldots ,z_m)$
if it is a solution of a polynomial functional equation
for some nonzero polynomial
![]() $P\in \mathbb {C}[z_1,\ldots ,z_m,z_{m+1}]$
. A function which is not algebraic is called a transcendental function. (We remark that an entire function in several variables is algebraic if and only if it is a polynomial function just as in the case of one variable.) Let
$P\in \mathbb {C}[z_1,\ldots ,z_m,z_{m+1}]$
. A function which is not algebraic is called a transcendental function. (We remark that an entire function in several variables is algebraic if and only if it is a polynomial function just as in the case of one variable.) Let
![]() $\mathbb {K}$
be a subset of
$\mathbb {K}$
be a subset of
![]() $\mathbb {C}$
and let f be an analytic function on the polydisc
$\mathbb {C}$
and let f be an analytic function on the polydisc
![]() $\Delta (0, \rho ):=B(0,\rho _1)\times \cdots \times B(0,\rho _m)\subseteq \mathbb {C}^m$
for some
$\Delta (0, \rho ):=B(0,\rho _1)\times \cdots \times B(0,\rho _m)\subseteq \mathbb {C}^m$
for some
![]() $\rho =(\rho _1,\ldots ,\rho _m)\in (0,\infty ]^m$
. We say that
$\rho =(\rho _1,\ldots ,\rho _m)\in (0,\infty ]^m$
. We say that
![]() $f\in \mathbb {K}[[z_1,\ldots ,z_m]]$
if
$f\in \mathbb {K}[[z_1,\ldots ,z_m]]$
if
 $$ \begin{align*} f(z_1,\ldots,z_m)=\sum_{(k_1,\ldots,k_m)\in \mathbb{Z}^m_{\geq 0}}c_{k_1,\ldots,k_m}z_1^{k_1}\cdots z_m^{k_m}, \end{align*} $$
$$ \begin{align*} f(z_1,\ldots,z_m)=\sum_{(k_1,\ldots,k_m)\in \mathbb{Z}^m_{\geq 0}}c_{k_1,\ldots,k_m}z_1^{k_1}\cdots z_m^{k_m}, \end{align*} $$
with
![]() $c_{k_1,\ldots ,k_m}\in \mathbb {K}$
for all
$c_{k_1,\ldots ,k_m}\in \mathbb {K}$
for all
![]() $(k_1,\ldots ,k_m)\in \mathbb {Z}^m_{\geq 0}$
and for all
$(k_1,\ldots ,k_m)\in \mathbb {Z}^m_{\geq 0}$
and for all
![]() $(z_1,\ldots ,z_m)\in \Delta (0,\rho )$
.
$(z_1,\ldots ,z_m)\in \Delta (0,\rho )$
.
The exceptional set
![]() $S_f$
of an analytic function
$S_f$
of an analytic function
![]() $f:\Omega \subseteq \mathbb {C}^m\to \mathbb {C}$
is defined as
$f:\Omega \subseteq \mathbb {C}^m\to \mathbb {C}$
is defined as
For example, let
![]() $f:\mathbb {C}^2\to \mathbb {C}$
and
$f:\mathbb {C}^2\to \mathbb {C}$
and
![]() $g:\mathbb {C}^2\to \mathbb {C}$
be the transcendental entire functions given by
$g:\mathbb {C}^2\to \mathbb {C}$
be the transcendental entire functions given by
By the Hermite–Lindemann theorem,
In general, if
![]() $P_1(X,Y),\ldots ,P_n(X,Y)\in \overline {\mathbb {Q}}[X,Y]$
, then the function
$P_1(X,Y),\ldots ,P_n(X,Y)\in \overline {\mathbb {Q}}[X,Y]$
, then the function
 $$ \begin{align*} f(w,z)=\exp\bigg(\prod_{k=1}^nP_k(w,z)\bigg) \end{align*} $$
$$ \begin{align*} f(w,z)=\exp\bigg(\prod_{k=1}^nP_k(w,z)\bigg) \end{align*} $$
has the exceptional set given by
 $$ \begin{align*} S_f=\bigcup_{k=1}^{n}\{(\alpha,\beta)\in\overline{\mathbb{Q}}^2 : P_k(\alpha,\beta)=0\}. \end{align*} $$
$$ \begin{align*} S_f=\bigcup_{k=1}^{n}\{(\alpha,\beta)\in\overline{\mathbb{Q}}^2 : P_k(\alpha,\beta)=0\}. \end{align*} $$
We refer the reader to [Reference Mahler1, Reference Waldschmidt5] (and references therein) for more about this subject.
In the main result of this paper, we shall prove that every subset S of
![]() $\overline {\mathbb {Q}}^m$
(under some mild conditions) is the exceptional set of uncountably many transcendental entire functions of several variables with rational coefficients.
$\overline {\mathbb {Q}}^m$
(under some mild conditions) is the exceptional set of uncountably many transcendental entire functions of several variables with rational coefficients.
Theorem 1.3. Let m be a positive integer. Then, every subset S of
![]() $\overline {\mathbb {Q}}^m$
, closed under complex conjugation and such that
$\overline {\mathbb {Q}}^m$
, closed under complex conjugation and such that
![]() $(0,\ldots ,0)\in S$
, is the exceptional set of uncountably many transcendental entire functions
$(0,\ldots ,0)\in S$
, is the exceptional set of uncountably many transcendental entire functions
![]() $f\in \mathbb {Q}[[z_1,\ldots ,z_m]]$
.
$f\in \mathbb {Q}[[z_1,\ldots ,z_m]]$
.
To prove this theorem, we shall provide a more general result about the arithmetic behaviour of a transcendental entire function of several variables.
Theorem 1.4. Let X be a countable subset of
![]() $\mathbb {C}^m$
and let
$\mathbb {C}^m$
and let
![]() $\mathbb {K}$
be a dense subset of
$\mathbb {K}$
be a dense subset of
![]() $\mathbb {C}$
. For each
$\mathbb {C}$
. For each
![]() $u\in X$
, fix a dense subset
$u\in X$
, fix a dense subset
![]() $E_{u}\subseteq \mathbb {C}$
and suppose that if
$E_{u}\subseteq \mathbb {C}$
and suppose that if
![]() $(0,\ldots ,0)\in X$
, then
$(0,\ldots ,0)\in X$
, then
![]() $E_{(0,\ldots ,0)}\cap \mathbb {K}\neq \emptyset $
. Then there exist uncountably many transcendental entire functions
$E_{(0,\ldots ,0)}\cap \mathbb {K}\neq \emptyset $
. Then there exist uncountably many transcendental entire functions
![]() $f\in \mathbb {K}[[z_1,\ldots ,z_m]]$
such that
$f\in \mathbb {K}[[z_1,\ldots ,z_m]]$
such that
![]() $f(u)\in E_{u}$
for all
$f(u)\in E_{u}$
for all
![]() $u\in X$
.
$u\in X$
.
Theorem 1.4 is a several variables extension of the one-variable result due to Marques and Ramirez [Reference Marques and Ramirez3, Theorem 1.3].
2 Proofs
2.1 Proof that Theorem 1.4 implies Theorem 1.3
In the statement of Theorem 1.4, choose
![]() $X=\overline {\mathbb {Q}}^m$
and
$X=\overline {\mathbb {Q}}^m$
and
![]() $\mathbb {K}=\mathbb {Q}^*+i\mathbb {Q}$
. Write
$\mathbb {K}=\mathbb {Q}^*+i\mathbb {Q}$
. Write
![]() $S=\{u_1,u_2,\ldots \}$
and
$S=\{u_1,u_2,\ldots \}$
and
![]() $\overline {\mathbb {Q}}^m/S=\{v_1,v_2,\ldots \}$
(one of them may be finite) and define
$\overline {\mathbb {Q}}^m/S=\{v_1,v_2,\ldots \}$
(one of them may be finite) and define
 $$ \begin{align*} E_u:=\begin{cases} \overline{\mathbb{Q}}& \mbox{if } u\in S,\\ \mathbb{K}\cdot\pi^n & \mbox{if } u=v_n. \end{cases} \end{align*} $$
$$ \begin{align*} E_u:=\begin{cases} \overline{\mathbb{Q}}& \mbox{if } u\in S,\\ \mathbb{K}\cdot\pi^n & \mbox{if } u=v_n. \end{cases} \end{align*} $$
By Theorem 1.4, there exist uncountably many transcendental entire functions
 $$ \begin{align*} f(z_1,\ldots,z_m)=\sum_{k_1\geq0,\ldots,k_m\geq0}c_{k_1,\ldots,k_m}z_1^{k_1}\cdots z_m^{k_m} \end{align*} $$
$$ \begin{align*} f(z_1,\ldots,z_m)=\sum_{k_1\geq0,\ldots,k_m\geq0}c_{k_1,\ldots,k_m}z_1^{k_1}\cdots z_m^{k_m} \end{align*} $$
in
![]() $\mathbb {K}[[z_1,\ldots ,z_m]]$
such that
$\mathbb {K}[[z_1,\ldots ,z_m]]$
such that
![]() $f(u)\in E_{u}$
for all
$f(u)\in E_{u}$
for all
![]() $u\in \overline {\mathbb {Q}}^m$
. Define
$u\in \overline {\mathbb {Q}}^m$
. Define
![]() $\psi (z_1,\ldots ,z_m)$
as
$\psi (z_1,\ldots ,z_m)$
as
 $$ \begin{align*} \psi(z_1,\ldots,z_m):=\frac{f(z_1,\ldots,z_m)+\overline{f(\overline{z_1},\ldots,\overline{z_m})}}{2}. \end{align*} $$
$$ \begin{align*} \psi(z_1,\ldots,z_m):=\frac{f(z_1,\ldots,z_m)+\overline{f(\overline{z_1},\ldots,\overline{z_m})}}{2}. \end{align*} $$
By the properties of the conjugation of power series,
 $$ \begin{align*} \psi(z_1,\ldots,z_m)=\sum_{(k_1,\ldots,k_m)\in \mathbb{Z}^m_{\geq 0}}\mathrm{Re}(c_{k_1,\ldots,k_m})z_1^{k_1}\cdots z_m^{k_m} \end{align*} $$
$$ \begin{align*} \psi(z_1,\ldots,z_m)=\sum_{(k_1,\ldots,k_m)\in \mathbb{Z}^m_{\geq 0}}\mathrm{Re}(c_{k_1,\ldots,k_m})z_1^{k_1}\cdots z_m^{k_m} \end{align*} $$
is a transcendental entire function in
![]() $\mathbb {Q}[[z_1,\ldots ,z_m]]$
since
$\mathbb {Q}[[z_1,\ldots ,z_m]]$
since
![]() $\mathrm{Re} (c_{k_1,\ldots ,k_m})$
is rational and nonzero for all
$\mathrm{Re} (c_{k_1,\ldots ,k_m})$
is rational and nonzero for all
![]() $(k_1,\ldots ,k_m)\in \mathbb {Z}^m_{\geq 0}$
by construction. (Here, as usual,
$(k_1,\ldots ,k_m)\in \mathbb {Z}^m_{\geq 0}$
by construction. (Here, as usual,
![]() $\mathrm{Re} (z)$
denotes the real part of the complex number z.)
$\mathrm{Re} (z)$
denotes the real part of the complex number z.)
Therefore, it suffices to prove that
![]() $S_{\psi }=S$
. In fact, since S is closed under complex conjugation, if
$S_{\psi }=S$
. In fact, since S is closed under complex conjugation, if
![]() $u\in S$
, then
$u\in S$
, then
![]() $\overline {u}\in S$
and thus
$\overline {u}\in S$
and thus
![]() $f(u)$
and
$f(u)$
and
![]() $\overline {f(\overline {u})}$
are algebraic numbers and so is
$\overline {f(\overline {u})}$
are algebraic numbers and so is
![]() $\psi (u)$
. (Observe also that
$\psi (u)$
. (Observe also that
![]() $f(0,\ldots ,0)=c_{0,\ldots ,0}\in \overline {\mathbb {Q}}$
.) In the case in which
$f(0,\ldots ,0)=c_{0,\ldots ,0}\in \overline {\mathbb {Q}}$
.) In the case in which
![]() $u=v_n$
, for some n, we can distinguish two cases. When
$u=v_n$
, for some n, we can distinguish two cases. When
![]() $v_n\in \mathbb {R}^{m}$
, then
$v_n\in \mathbb {R}^{m}$
, then
![]() $\psi (u)=\mathrm{Re} (f(v_n))$
is transcendental, since
$\psi (u)=\mathrm{Re} (f(v_n))$
is transcendental, since
![]() $f(v_n)\in \mathbb {K}\cdot \pi ^n$
. For
$f(v_n)\in \mathbb {K}\cdot \pi ^n$
. For
![]() $v_n\notin \mathbb {R}^m$
, we have
$v_n\notin \mathbb {R}^m$
, we have
![]() $\overline {v_n}=v_l$
for some
$\overline {v_n}=v_l$
for some
![]() $l\neq n$
. Thus, there exist nonzero algebraic numbers
$l\neq n$
. Thus, there exist nonzero algebraic numbers
![]() $\gamma _1, \gamma _2$
such that
$\gamma _1, \gamma _2$
such that
which is transcendental, since
![]() $\overline {\mathbb {Q}}$
is algebraically closed and
$\overline {\mathbb {Q}}$
is algebraically closed and
![]() $\pi $
is transcendental. In conclusion,
$\pi $
is transcendental. In conclusion,
![]() $\psi \in \mathbb {Q}[[z_1,\ldots ,z_m]]$
is a transcendental entire function whose exceptional set is S.
$\psi \in \mathbb {Q}[[z_1,\ldots ,z_m]]$
is a transcendental entire function whose exceptional set is S.
2.2 Proof of Theorem 1.4
Let us proceed by induction on m. The case
![]() $m=1$
is covered by Lemma 1.2. Suppose that the theorem holds for all positive integers
$m=1$
is covered by Lemma 1.2. Suppose that the theorem holds for all positive integers
![]() $k\in [1,m-1]$
. That is, if
$k\in [1,m-1]$
. That is, if
![]() $\mathbb {K}$
is a dense subset of
$\mathbb {K}$
is a dense subset of
![]() $\mathbb {C}$
, X is a countable subset of
$\mathbb {C}$
, X is a countable subset of
![]() $\mathbb {C}^k$
and
$\mathbb {C}^k$
and
![]() $E_u$
is a dense subset in
$E_u$
is a dense subset in
![]() $\mathbb {C}$
for each
$\mathbb {C}$
for each
![]() $u\in X$
, then there exist uncountably many transcendental entire functions
$u\in X$
, then there exist uncountably many transcendental entire functions
![]() $f\in \mathbb {K}[[z_1,\ldots ,z_k]]$
such that
$f\in \mathbb {K}[[z_1,\ldots ,z_k]]$
such that
![]() $f(u)\in E_u$
for all
$f(u)\in E_u$
for all
![]() $u\in X$
, for any integer
$u\in X$
, for any integer
![]() $k\in [1, m-1]$
.
$k\in [1, m-1]$
.
Now, let X be a countable subset of
![]() $\mathbb {C}^{m}$
and
$\mathbb {C}^{m}$
and
![]() $E_u$
a fixed dense subset of
$E_u$
a fixed dense subset of
![]() $\mathbb {C}$
for all
$\mathbb {C}$
for all
![]() $u\in X$
. Without loss of generality, we can assume that
$u\in X$
. Without loss of generality, we can assume that
![]() $(0,\ldots ,0) \in X$
. In this case, by hypothesis,
$(0,\ldots ,0) \in X$
. In this case, by hypothesis,
![]() $\mathbb {K} \cap E_{(0,\ldots ,0)} \neq \emptyset $
. To apply the induction hypothesis, we consider the partition of X given by
$\mathbb {K} \cap E_{(0,\ldots ,0)} \neq \emptyset $
. To apply the induction hypothesis, we consider the partition of X given by
 $$ \begin{align*} X=\bigcup_{S\in \mathcal{P}_{m}}X_{S}, \end{align*} $$
$$ \begin{align*} X=\bigcup_{S\in \mathcal{P}_{m}}X_{S}, \end{align*} $$
where
![]() $\mathcal {P}_{m}$
denotes the powerset of
$\mathcal {P}_{m}$
denotes the powerset of
![]() $[1,m]=\{1,\ldots ,m\}$
and
$[1,m]=\{1,\ldots ,m\}$
and
![]() $X_S$
denotes the set of all
$X_S$
denotes the set of all
![]() $z=(z_1,\ldots ,z_{m})$
in
$z=(z_1,\ldots ,z_{m})$
in
![]() $X\subseteq \mathbb {C}^{m}$
such that
$X\subseteq \mathbb {C}^{m}$
such that
![]() $z_i\neq 0$
if and only if
$z_i\neq 0$
if and only if
![]() $i\in S$
. In particular,
$i\in S$
. In particular,
![]() $X_{\emptyset }=\{(0,\ldots ,0)\}$
and
$X_{\emptyset }=\{(0,\ldots ,0)\}$
and
![]() $X_{[1,m]} = X\cap (\mathbb {C} \setminus \{0\})^m$
.
$X_{[1,m]} = X\cap (\mathbb {C} \setminus \{0\})^m$
.
Given
![]() $S=\{i_1,\ldots ,i_k\}$
in
$S=\{i_1,\ldots ,i_k\}$
in
![]() $\mathcal {Q}_{m}=\mathcal {P}_m \setminus \{\emptyset ,[1,m]\}$
and
$\mathcal {Q}_{m}=\mathcal {P}_m \setminus \{\emptyset ,[1,m]\}$
and
![]() $z=(z_1,\ldots ,z_{m})$
in
$z=(z_1,\ldots ,z_{m})$
in
![]() $\mathbb {C}^m$
, we denote by
$\mathbb {C}^m$
, we denote by
![]() $z_{S}$
the element
$z_{S}$
the element
![]() $(z_{i_1},\ldots ,z_{i_k})\in \mathbb {C}^k.$
To simplify the exposition, we will assume that
$(z_{i_1},\ldots ,z_{i_k})\in \mathbb {C}^k.$
To simplify the exposition, we will assume that
![]() $i_1<\cdots <i_k$
for all
$i_1<\cdots <i_k$
for all
![]() $S\in \mathcal {Q}_m$
. Our goal is to show that there exist uncountably many ways to construct a transcendental entire function
$S\in \mathcal {Q}_m$
. Our goal is to show that there exist uncountably many ways to construct a transcendental entire function
![]() $f \in \mathbb {K}[[z_1, \ldots , z_m]]$
given by
$f \in \mathbb {K}[[z_1, \ldots , z_m]]$
given by
 $$ \begin{align*} f(z_1,\ldots,z_{m})=a_0+\bigg(\sum_{S\in\mathcal{Q}_m}\bigg(\prod_{i\in S}z_i\bigg)f_S(z_S)\bigg)+f^*(z_1,\ldots,z_{m}), \end{align*} $$
$$ \begin{align*} f(z_1,\ldots,z_{m})=a_0+\bigg(\sum_{S\in\mathcal{Q}_m}\bigg(\prod_{i\in S}z_i\bigg)f_S(z_S)\bigg)+f^*(z_1,\ldots,z_{m}), \end{align*} $$
where
![]() $a_0\in E_{(0,\ldots ,0)}\cap \mathbb {K}$
and, for each
$a_0\in E_{(0,\ldots ,0)}\cap \mathbb {K}$
and, for each
![]() $S=\{i_1,\ldots ,i_k\}\in \mathcal {Q}_m$
, the function
$S=\{i_1,\ldots ,i_k\}\in \mathcal {Q}_m$
, the function
![]() $f_S:\mathbb {C}^k\to \mathbb {C}$
is a transcendental entire function such that
$f_S:\mathbb {C}^k\to \mathbb {C}$
is a transcendental entire function such that
 $$ \begin{align*} f_S(u_S)\in \frac{1}{\alpha_{i_1}\cdots \alpha_{i_k}}\cdot(E_u-\Theta_{S,u}) \end{align*} $$
$$ \begin{align*} f_S(u_S)\in \frac{1}{\alpha_{i_1}\cdots \alpha_{i_k}}\cdot(E_u-\Theta_{S,u}) \end{align*} $$
for all
![]() $u=(\alpha _1,\ldots ,\alpha _{m})\in X_S$
with
$u=(\alpha _1,\ldots ,\alpha _{m})\in X_S$
with
 $$ \begin{align*} \Theta_{S,u}=a_0+\sum_{T\in\mathcal{Q}_m,T\neq S}\bigg(\prod_{i\in T}\alpha_i\bigg)f_T(u_T)\in\mathbb{C}. \end{align*} $$
$$ \begin{align*} \Theta_{S,u}=a_0+\sum_{T\in\mathcal{Q}_m,T\neq S}\bigg(\prod_{i\in T}\alpha_i\bigg)f_T(u_T)\in\mathbb{C}. \end{align*} $$
By the induction hypothesis,
![]() $f_S$
exists for all
$f_S$
exists for all
![]() $S\in \mathcal {Q}_m$
(noting that if
$S\in \mathcal {Q}_m$
(noting that if
![]() $E_u$
is a dense subset of
$E_u$
is a dense subset of
![]() $\mathbb {C}$
, then
$\mathbb {C}$
, then
![]() $(\alpha _{i_1}\cdots \alpha _{i_k})^{-1}\cdot (E_u-\Theta _{S,u})$
is also a dense set). Moreover, we want the function
$(\alpha _{i_1}\cdots \alpha _{i_k})^{-1}\cdot (E_u-\Theta _{S,u})$
is also a dense set). Moreover, we want the function
![]() $f^*(z_1,\ldots ,z_m)\in \mathbb {K}[[z_1,\ldots ,z_m]]$
to satisfy the condition
$f^*(z_1,\ldots ,z_m)\in \mathbb {K}[[z_1,\ldots ,z_m]]$
to satisfy the condition
 $$ \begin{align} f^*(u)\in \bigg(E_u-a_0-\sum_{S\in\mathcal{Q}_m}\bigg(\prod_{i\in S}\alpha_i\bigg)f_S(u_S)\bigg) \end{align} $$
$$ \begin{align} f^*(u)\in \bigg(E_u-a_0-\sum_{S\in\mathcal{Q}_m}\bigg(\prod_{i\in S}\alpha_i\bigg)f_S(u_S)\bigg) \end{align} $$
for all
![]() $u=(\alpha _1,\ldots ,\alpha _m)\in X_{[1,m]}$
, and
$u=(\alpha _1,\ldots ,\alpha _m)\in X_{[1,m]}$
, and
![]() $f^*(z_1,\ldots ,z_m)=0$
whenever
$f^*(z_1,\ldots ,z_m)=0$
whenever
![]() $z_i=0$
for some i with
$z_i=0$
for some i with
![]() $1\leq i\leq m$
. Under these conditions, it is easy to see that if
$1\leq i\leq m$
. Under these conditions, it is easy to see that if
![]() $S\in \mathcal {Q}_m$
and
$S\in \mathcal {Q}_m$
and
![]() $u\in X_S$
, then
$u\in X_S$
, then
![]() $f^*(u)=0$
and
$f^*(u)=0$
and
![]() $f(u)\in E_u$
.
$f(u)\in E_u$
.
To construct the function
![]() $f^*:\mathbb {C}^m\to \mathbb {C},$
let us consider an enumeration
$f^*:\mathbb {C}^m\to \mathbb {C},$
let us consider an enumeration
![]() $\{u_1,u_2,\ldots \}$
of
$\{u_1,u_2,\ldots \}$
of
![]() $X_{[1,m]}$
, where we write
$X_{[1,m]}$
, where we write
![]() $u_j=(\alpha _1^{(j)},\ldots ,\alpha _{m}^{(j)})$
. We construct a function
$u_j=(\alpha _1^{(j)},\ldots ,\alpha _{m}^{(j)})$
. We construct a function
![]() $f^*\in \mathbb {K}[[z_1,\ldots ,z_m]]$
given by
$f^*\in \mathbb {K}[[z_1,\ldots ,z_m]]$
given by
 $$ \begin{align*} f^*(z_1,\ldots,z_{m})=\sum_{n=m}^{\infty}P_n(z_1,\ldots,z_{m})=\sum_{i_1\geq1,\ldots,i_m\geq1}c_{i_1,\ldots,i_m}z_1^{i_1}\cdots z_m^{i_m}, \end{align*} $$
$$ \begin{align*} f^*(z_1,\ldots,z_{m})=\sum_{n=m}^{\infty}P_n(z_1,\ldots,z_{m})=\sum_{i_1\geq1,\ldots,i_m\geq1}c_{i_1,\ldots,i_m}z_1^{i_1}\cdots z_m^{i_m}, \end{align*} $$
where
![]() $P_n$
is a homogeneous polynomial of degree n and the coefficients
$P_n$
is a homogeneous polynomial of degree n and the coefficients
![]() $c_{i_1,\ldots ,i_m}\in \mathbb {K}$
will be chosen so that
$c_{i_1,\ldots ,i_m}\in \mathbb {K}$
will be chosen so that
![]() $f^*$
will satisfy the desired conditions.
$f^*$
will satisfy the desired conditions.
The first condition is
 $$ \begin{align*} |c_{i_1,\ldots,i_m}|<s_{i_1+\cdots+i_m}:=\frac{1}{\binom{i_1+\cdots+i_m-1}{m-1}(i_1+\cdots+i_m)!}, \end{align*} $$
$$ \begin{align*} |c_{i_1,\ldots,i_m}|<s_{i_1+\cdots+i_m}:=\frac{1}{\binom{i_1+\cdots+i_m-1}{m-1}(i_1+\cdots+i_m)!}, \end{align*} $$
where
![]() $c_{i_1,\ldots ,i_n}\neq 0$
for infinitely many m-tuples of integers
$c_{i_1,\ldots ,i_n}\neq 0$
for infinitely many m-tuples of integers
![]() $i_1\geq 1, \ldots , i_m\geq 1$
. These conditions will be used to guarantee that
$i_1\geq 1, \ldots , i_m\geq 1$
. These conditions will be used to guarantee that
![]() $f^*$
is an entire function. Let
$f^*$
is an entire function. Let
![]() $L(P)$
denote the length of the polynomial
$L(P)$
denote the length of the polynomial
![]() $P(z_1,\ldots ,z_m)\in \mathbb {C}[z_1,\ldots ,z_m]$
given by the sum of the absolute values of its coefficients. Since
$P(z_1,\ldots ,z_m)\in \mathbb {C}[z_1,\ldots ,z_m]$
given by the sum of the absolute values of its coefficients. Since
for all
![]() $n\geq m$
and
$n\geq m$
and
![]() $(z_1,\ldots ,z_m)$
belonging to the open ball
$(z_1,\ldots ,z_m)$
belonging to the open ball
![]() $B(0,R)$
,
$B(0,R)$
,
 $$ \begin{align*} |P_n(z_1,\ldots,z_m)|<\frac{\binom{n-1}{m-1}}{\binom{n-1}{m-1}n!}\max\{1,R\}^{n}=\frac{\max\{1,R\}^{n}}{n!}, \end{align*} $$
$$ \begin{align*} |P_n(z_1,\ldots,z_m)|<\frac{\binom{n-1}{m-1}}{\binom{n-1}{m-1}n!}\max\{1,R\}^{n}=\frac{\max\{1,R\}^{n}}{n!}, \end{align*} $$
since
![]() $P_n(z_1,\ldots ,z_m)$
has at most
$P_n(z_1,\ldots ,z_m)$
has at most
![]() $\binom {n-1}{m-1}$
monomials of degree n. Hence, the series
$\binom {n-1}{m-1}$
monomials of degree n. Hence, the series
![]() $\sum _{n\geq m}P_n(z_1,\ldots ,z_m)$
converges uniformly in any of these balls. Thus,
$\sum _{n\geq m}P_n(z_1,\ldots ,z_m)$
converges uniformly in any of these balls. Thus,
![]() $f^*$
is a transcendental entire function such that
$f^*$
is a transcendental entire function such that
![]() $f^*(0,z_2,\ldots ,z_m)=f^*(z_1,0,z_3,\ldots ,z_m)=f^*(z_1,z_2,\ldots ,0)=0$
.
$f^*(0,z_2,\ldots ,z_m)=f^*(z_1,0,z_3,\ldots ,z_m)=f^*(z_1,z_2,\ldots ,0)=0$
.
To obtain the coefficients
![]() $c_{i_1,\ldots ,i_m}\in \mathbb {K}$
such that
$c_{i_1,\ldots ,i_m}\in \mathbb {K}$
such that
![]() $f^*$
satisfies the condition (2.1), we consider a hyperplane
$f^*$
satisfies the condition (2.1), we consider a hyperplane
![]() $\pi (n,j)$
for positive integers n and j with
$\pi (n,j)$
for positive integers n and j with
![]() $1\leq j \leq n$
, given by
$1\leq j \leq n$
, given by
and such that if
![]() $u_j$
,
$u_j$
,
![]() $u_{n+1}$
and the origin are noncollinear, then
$u_{n+1}$
and the origin are noncollinear, then
![]() $\pi (n,j)$
is a hyperplane containing
$\pi (n,j)$
is a hyperplane containing
![]() $u_j$
and parallel to the line passing through the origin and the point
$u_j$
and parallel to the line passing through the origin and the point
![]() $u_{n+1},$
and, if
$u_{n+1},$
and, if
![]() $u_j$
,
$u_j$
,
![]() $u_{n+1}$
and the origin are collinear, then
$u_{n+1}$
and the origin are collinear, then
![]() $\pi (n,j)$
is a hyperplane containing
$\pi (n,j)$
is a hyperplane containing
![]() $u_j$
and perpendicular to the line passing through the origin and the point
$u_j$
and perpendicular to the line passing through the origin and the point
![]() $u_{n+1}$
. Note that in both cases,
$u_{n+1}$
. Note that in both cases,
![]() $\lambda _n^{(j)}\neq 0$
and
$\lambda _n^{(j)}\neq 0$
and
![]() $u_{n+1}$
does not belong to any hyperplane
$u_{n+1}$
does not belong to any hyperplane
![]() $\pi (n,j)$
with
$\pi (n,j)$
with
![]() $1\leq j\leq n$
.
$1\leq j\leq n$
.
Now, we define the polynomials
![]() $A_0(z_1,\ldots ,z_m):=z_1\cdots z_m$
and
$A_0(z_1,\ldots ,z_m):=z_1\cdots z_m$
and
 $$ \begin{align*} A_n(z_1,\ldots,z_{m}):=\prod_{j=1}^{n}(\mu_{n,1}^{(j)}z_1+\cdots+\mu_{n,m}^{(j)}z_m-\lambda_n^{(j)}) \end{align*} $$
$$ \begin{align*} A_n(z_1,\ldots,z_{m}):=\prod_{j=1}^{n}(\mu_{n,1}^{(j)}z_1+\cdots+\mu_{n,m}^{(j)}z_m-\lambda_n^{(j)}) \end{align*} $$
for all
![]() $n\geq 1$
. By the definition of
$n\geq 1$
. By the definition of
![]() $\pi (n,j)$
, we have
$\pi (n,j)$
, we have
![]() $A_n(u_j)=0$
for
$A_n(u_j)=0$
for
![]() $1\leq j\leq n$
. Since
$1\leq j\leq n$
. Since
![]() $u_{n+1}$
and the origin do not belong to
$u_{n+1}$
and the origin do not belong to
![]() $\pi (n,j)$
, we also have
$\pi (n,j)$
, we also have
![]() $A_n(0,\ldots ,0)\neq 0$
and
$A_n(0,\ldots ,0)\neq 0$
and
![]() $A_n(u_{n+1})\neq 0$
for all
$A_n(u_{n+1})\neq 0$
for all
![]() $n\geq 1$
. Thus, we can define the function
$n\geq 1$
. Thus, we can define the function
such that
![]() $\Theta _1+f_{1,0}^*(u_1)\in E_{u_1}$
and
$\Theta _1+f_{1,0}^*(u_1)\in E_{u_1}$
and
![]() $0<|\delta _{1,0}|<s_m/m$
, where
$0<|\delta _{1,0}|<s_m/m$
, where
 $$ \begin{align*} \Theta_j:=a_0+\sum_{S\in \mathcal{Q}_m}\bigg(\prod_{i\in S}\alpha_i^{(j)}\bigg)f_S(u_{j,S}), \end{align*} $$
$$ \begin{align*} \Theta_j:=a_0+\sum_{S\in \mathcal{Q}_m}\bigg(\prod_{i\in S}\alpha_i^{(j)}\bigg)f_S(u_{j,S}), \end{align*} $$
and
![]() $u_{j,S}=(\alpha _{i_1}^{(j)},\ldots ,\alpha _{i_k}^{(j)})$
for
$u_{j,S}=(\alpha _{i_1}^{(j)},\ldots ,\alpha _{i_k}^{(j)})$
for
![]() $S=\{i_1,\ldots ,i_k\}$
, for all integers
$S=\{i_1,\ldots ,i_k\}$
, for all integers
![]() $j\geq 1$
.
$j\geq 1$
.
Since
![]() $\mathbb {K}$
is a dense subset of
$\mathbb {K}$
is a dense subset of
![]() $\mathbb {C}$
, we can choose
$\mathbb {C}$
, we can choose
![]() $\delta _{1,1}$
such that the coefficient
$\delta _{1,1}$
such that the coefficient
![]() $c_{1,1,\ldots ,1}$
of
$c_{1,1,\ldots ,1}$
of
![]() $z_1\cdots z_m$
in the function
$z_1\cdots z_m$
in the function
belongs to
![]() $\mathbb {K}$
with
$\mathbb {K}$
with
![]() $|c_{1,1,\ldots ,1}|<s_m$
. Therefore, we take
$|c_{1,1,\ldots ,1}|<s_m$
. Therefore, we take
where
![]() $P_1(z_1,\ldots ,z_m)=c_{1,1,\ldots ,1}z_1\cdots z_m$
.
$P_1(z_1,\ldots ,z_m)=c_{1,1,\ldots ,1}z_1\cdots z_m$
.
Recursively, we can construct a function
![]() $f^*_{n,0}(z_1,\ldots ,z_{m})$
given by
$f^*_{n,0}(z_1,\ldots ,z_{m})$
given by
where we take
![]() $\delta _{n,0}\neq 0$
in the ball
$\delta _{n,0}\neq 0$
in the ball
![]() $B(0,s_{n+m-1}/(n+m-1))$
such that
$B(0,s_{n+m-1}/(n+m-1))$
such that
This is possible since
![]() $E_{u_n}$
is a dense subset of
$E_{u_n}$
is a dense subset of
![]() $\mathbb {C}$
and all coordinates of
$\mathbb {C}$
and all coordinates of
![]() $u_n$
are nonzero.
$u_n$
are nonzero.
Since
![]() $\mathbb {K}$
is a dense subset of
$\mathbb {K}$
is a dense subset of
![]() $\mathbb {C}$
, if we consider the ordering of the monomials of degree
$\mathbb {C}$
, if we consider the ordering of the monomials of degree
![]() $n+m-1$
given by the lexicographical order of the exponents, then we can choose
$n+m-1$
given by the lexicographical order of the exponents, then we can choose
![]() $\delta _{n,l}$
such that the coefficient
$\delta _{n,l}$
such that the coefficient
![]() $c_{j_1,\ldots ,j_m}$
of the lth monomial
$c_{j_1,\ldots ,j_m}$
of the lth monomial
![]() $z_1^{j_1}\cdots z_m^{j_m}$
in
$z_1^{j_1}\cdots z_m^{j_m}$
in
belongs to
![]() $\mathbb {K}$
with
$\mathbb {K}$
with
![]() $|c_{j_1,\ldots ,j_m}|<s_{n+m-1}$
. Thus, we define
$|c_{j_1,\ldots ,j_m}|<s_{n+m-1}$
. Thus, we define
where
![]() $L=\binom {n+m-2}{m-1}$
is the number of distinct monomials of degree
$L=\binom {n+m-2}{m-1}$
is the number of distinct monomials of degree
![]() $n+m-1$
. Then
$n+m-1$
. Then
![]() $f^*_n(z_1,\ldots ,z_m)$
is a polynomial function such that
$f^*_n(z_1,\ldots ,z_m)$
is a polynomial function such that
![]() $c_{j_1,\ldots ,j_m}\in \mathbb {K}$
for every m-tuple
$c_{j_1,\ldots ,j_m}\in \mathbb {K}$
for every m-tuple
![]() $(j_1,\ldots ,j_m)$
such that
$(j_1,\ldots ,j_m)$
such that
![]() $j_1+\cdots +j_m\leq n+m-1$
.
$j_1+\cdots +j_m\leq n+m-1$
.
Finally, this construction implies that the functions
![]() $f^*_n$
converge to a transcendental entire function
$f^*_n$
converge to a transcendental entire function
![]() $f^*\in \mathbb {K}[[z_1,\ldots ,z_m]]$
as
$f^*\in \mathbb {K}[[z_1,\ldots ,z_m]]$
as
![]() $n\to \infty $
such that
$n\to \infty $
such that
for all
![]() $n\geq j\geq 1$
. Let
$n\geq j\geq 1$
. Let
![]() $f:\mathbb {C}^{m}\to \mathbb {C}$
be the entire function given by
$f:\mathbb {C}^{m}\to \mathbb {C}$
be the entire function given by
 $$ \begin{align*} f(z_1,\ldots,z_{m})=a_0+\bigg(\sum_{S\in\mathcal{Q}_m}\bigg(\prod_{i\in S}z_i\bigg)f_S(z_S)\bigg)+f^*(z_1,\ldots,z_{m}). \end{align*} $$
$$ \begin{align*} f(z_1,\ldots,z_{m})=a_0+\bigg(\sum_{S\in\mathcal{Q}_m}\bigg(\prod_{i\in S}z_i\bigg)f_S(z_S)\bigg)+f^*(z_1,\ldots,z_{m}). \end{align*} $$
Then
![]() $f(u)\in E_u$
for all
$f(u)\in E_u$
for all
![]() $u\in X\subset \mathbb {C}^{m}$
. Since f is an entire function that is not a polynomial, it follows that f is transcendental. Note that there are uncountably many ways to choose the constants
$u\in X\subset \mathbb {C}^{m}$
. Since f is an entire function that is not a polynomial, it follows that f is transcendental. Note that there are uncountably many ways to choose the constants
![]() $\delta _{n,j}$
. This completes the proof.
$\delta _{n,j}$
. This completes the proof.
Acknowledgments
The authors are grateful to the referee for their valuable suggestions about this paper. Part of this work was done during a visit by Diego Marques to University of Hradec Králové (Czech Republic) which provided excellent working conditions.