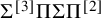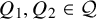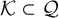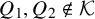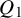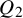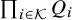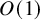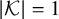1 Introduction
This paper studies a problem at the intersection of algebraic complexity, algebraic geometry and combinatorics that is motivated by the polynomial identity testing problem (PIT for short) for depth
![]() $4$
circuits. The question can also be regarded as an algebraic generalization and extension of the famous Sylvester–Gallai theorem from discrete geometry. We next describe the Sylvester–Gallai theorem and some of its many extensions and generalizations. For the relation to the PIT problem, see e.g. [Reference Shpilka20].
$4$
circuits. The question can also be regarded as an algebraic generalization and extension of the famous Sylvester–Gallai theorem from discrete geometry. We next describe the Sylvester–Gallai theorem and some of its many extensions and generalizations. For the relation to the PIT problem, see e.g. [Reference Shpilka20].
Sylvester–Gallai-type theorems:
The Sylvester–Gallai theorem asserts that, if a finite set of points in
![]() $\mathbb {R}^n$
has the property that every line passing through any two points in the set also contains a third point in the set, then all the points in the set are colinear [Reference Melchior16, Reference Gallai10]. Kelly extended the theorem to points in
$\mathbb {R}^n$
has the property that every line passing through any two points in the set also contains a third point in the set, then all the points in the set are colinear [Reference Melchior16, Reference Gallai10]. Kelly extended the theorem to points in
![]() $\mathbb {C}^n$
and proved that, if a finite set of points satisfy the Sylvester–Gallai condition, then the points in the set are coplanar. Many variants of this theorem were studied: extensions to higher dimensions, colored versions, robust versions and many more. For more on the Sylvester–Gallai theorem and some of its variants, see [Reference Borwein and Moser4, Reference Barak, Dvir, Wigderson and Yehudayoff1, Reference Dvir, Saraf and Wigderson8].
$\mathbb {C}^n$
and proved that, if a finite set of points satisfy the Sylvester–Gallai condition, then the points in the set are coplanar. Many variants of this theorem were studied: extensions to higher dimensions, colored versions, robust versions and many more. For more on the Sylvester–Gallai theorem and some of its variants, see [Reference Borwein and Moser4, Reference Barak, Dvir, Wigderson and Yehudayoff1, Reference Dvir, Saraf and Wigderson8].
There are two extensions that are highly relevant to this work: The colored version, proved by Edelstein and Kelly, states that, if three finite sets of points satisfy that every line passing through points from two different sets also contain a point from the third set, then all the points belong to a low-dimensional space. This result was further extended to any constant number of sets. The robust version, obtained in [Reference Barak, Dvir, Wigderson and Yehudayoff1, Reference Dvir, Saraf and Wigderson8], states that, if a finite set of points satisfy that, for every point p in the set, a
![]() $\delta $
fraction of the other points satisfy that the line passing through each of them and p spans a third point in the set, then the set is contained in an
$\delta $
fraction of the other points satisfy that the line passing through each of them and p spans a third point in the set, then the set is contained in an
![]() $O(1/\delta )$
-dimensional space.
$O(1/\delta )$
-dimensional space.
Although the Sylvester–Gallai theorem is formulated as a geometric question, it can be stated in algebraic terms: If a finite set of pairwise linearly independent vectors,
![]() ${\mathcal {S}} \subset \mathbb {C}^n$
, has the property that every two vectors span a third vector in the set, then the dimension of
${\mathcal {S}} \subset \mathbb {C}^n$
, has the property that every two vectors span a third vector in the set, then the dimension of
![]() ${\mathcal {S}}$
is at most
${\mathcal {S}}$
is at most
![]() $3$
. It is not very hard to see that, if we pick a subspace H, of codimension
$3$
. It is not very hard to see that, if we pick a subspace H, of codimension
![]() $1$
, which is in general position with respect to the vectors in the set, then the intersection points
$1$
, which is in general position with respect to the vectors in the set, then the intersection points
![]() $p_i = H \cap \operatorname {span}\{{s_i}\}$
, for
$p_i = H \cap \operatorname {span}\{{s_i}\}$
, for
![]() $s_i\in {\mathcal {S}}$
satisfy the Sylvester–Gallai condition. Therefore,
$s_i\in {\mathcal {S}}$
satisfy the Sylvester–Gallai condition. Therefore,
![]() $\dim (S) \leq 3$
. Another formulation is the following: If a finite set of pairwise linearly independent linear forms,
$\dim (S) \leq 3$
. Another formulation is the following: If a finite set of pairwise linearly independent linear forms,
![]() ${\mathcal {L}} \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
, has the property that, for every two forms
${\mathcal {L}} \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
, has the property that, for every two forms
![]() $\ell _i,\ell _j \in {\mathcal {L}}$
, there is a third form
$\ell _i,\ell _j \in {\mathcal {L}}$
, there is a third form
![]() $\ell _k \in {\mathcal {L}}$
, so that, whenever
$\ell _k \in {\mathcal {L}}$
, so that, whenever
![]() $\ell _i$
and
$\ell _i$
and
![]() $\ell _j$
vanish, then so does
$\ell _j$
vanish, then so does
![]() $\ell _k$
, then the linear dimension of
$\ell _k$
, then the linear dimension of
![]() ${\mathcal {L}}$
is at most
${\mathcal {L}}$
is at most
![]() $3$
. To see this, note that it must be the case that
$3$
. To see this, note that it must be the case that
![]() $\ell _k \in \operatorname {span}\{{\ell _i,\ell _j}\}$
and thus the coefficient vectors of the forms in the set satisfy the condition of the (vector version of the) Sylvester–Gallai theorem, and the bound on the dimension follows.
$\ell _k \in \operatorname {span}\{{\ell _i,\ell _j}\}$
and thus the coefficient vectors of the forms in the set satisfy the condition of the (vector version of the) Sylvester–Gallai theorem, and the bound on the dimension follows.
The last formulation can now be extended to higher-degree polynomials. In particular, the following question was asked by Gupta [Reference Gupta12].
Problem 1.1 (Restatement of Conjecture 2 of [Reference Gupta12]).
Can we bound the linear dimension or algebraic rank of a finite set
![]() ${\mathcal {P}}$
of pairwise linearly independent, irreducible, homogeneous polynomials of degree at most r in
${\mathcal {P}}$
of pairwise linearly independent, irreducible, homogeneous polynomials of degree at most r in
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
that has the following property: For any two distinct polynomials
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
that has the following property: For any two distinct polynomials
![]() $P_1,P_2 \in {\mathcal {P}}$
there is a third polynomial
$P_1,P_2 \in {\mathcal {P}}$
there is a third polynomial
![]() $P_3 \in {\mathcal {P}}$
such that, whenever
$P_3 \in {\mathcal {P}}$
such that, whenever
![]() $P_1,P_2$
vanish, then so does
$P_1,P_2$
vanish, then so does
![]() $P_3$
.
$P_3$
.
A robust or colored version of this problem can also be formulated. As we have seen, the case
![]() $r=1$
, that is, when all the polynomials are linear forms, follows from the Sylvester–Gallai theorem. For the case of quadratic polynomials, that is,
$r=1$
, that is, when all the polynomials are linear forms, follows from the Sylvester–Gallai theorem. For the case of quadratic polynomials, that is,
![]() $r=2$
, [Reference Shpilka20] gave a bound on the linear dimension for both the noncolored and colored versions. Recently, Oliveira and Sengupta solved the case
$r=2$
, [Reference Shpilka20] gave a bound on the linear dimension for both the noncolored and colored versions. Recently, Oliveira and Sengupta solved the case
![]() $r=3$
[Reference de Oliveira and Sengupta7]. In [Reference Peleg, Shpilka, Goaoc and Kerber18, Reference Garg, Oliveira and Sengupta11] a bound for the robust version for
$r=3$
[Reference de Oliveira and Sengupta7]. In [Reference Peleg, Shpilka, Goaoc and Kerber18, Reference Garg, Oliveira and Sengupta11] a bound for the robust version for
![]() $r=2$
was proved. For degrees,
$r=2$
was proved. For degrees,
![]() $r \geq 4$
, the problem is still open. Gupta [Reference Gupta12] also raised more general questions of a similar form. As Gupta’s general question is for a colored version of the problem, we state a version of his Conjecture 32 that is in the spirit of this work and that is still open for degrees
$r \geq 4$
, the problem is still open. Gupta [Reference Gupta12] also raised more general questions of a similar form. As Gupta’s general question is for a colored version of the problem, we state a version of his Conjecture 32 that is in the spirit of this work and that is still open for degrees
![]() $r\geq 3$
.
$r\geq 3$
.
Problem 1.2. Can we bound the linear dimension or algebraic rank of a finite set
![]() ${\mathcal {P}}$
of pairwise linearly independent irreducible polynomials of degree at most r in
${\mathcal {P}}$
of pairwise linearly independent irreducible polynomials of degree at most r in
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
that has the following property: For any two distinct polynomials
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
that has the following property: For any two distinct polynomials
![]() $P_1,P_2 \in {\mathcal {P}}$
, there is a subset
$P_1,P_2 \in {\mathcal {P}}$
, there is a subset
![]() ${\mathcal {I}} \subset {\mathcal {P}}$
such that
${\mathcal {I}} \subset {\mathcal {P}}$
such that
![]() $P_1,P_2 \notin {\mathcal {I}}$
and whenever
$P_1,P_2 \notin {\mathcal {I}}$
and whenever
![]() $P_1,P_2$
vanish, then so does
$P_1,P_2$
vanish, then so does
![]() $\prod _{P_i\in {\mathcal {I}}} P_i$
?
$\prod _{P_i\in {\mathcal {I}}} P_i$
?
As before, this problem can also be extended to robust and colored versions. In the case of linear forms, the bound for Theorem 1.1 carries over to Theorem 1.2 as well. This follows from the fact that the ideal generated by linear forms is prime (see section 2 for definitions). In the case of higher-degree polynomials, there is no clear reduction. For example, let
![]() $r=2$
and
$r=2$
and
It is not hard to verify that whenever
![]() $P_1$
and
$P_1$
and
![]() $P_2$
vanish, then so does
$P_2$
vanish, then so does
![]() $P_3 \cdot P_4$
, but neither
$P_3 \cdot P_4$
, but neither
![]() $P_3$
nor
$P_3$
nor
![]() $P_4$
always vanishes when
$P_4$
always vanishes when
![]() $P_1$
and
$P_1$
and
![]() $P_2$
do. The reason is that the radical of the ideal generated by
$P_2$
do. The reason is that the radical of the ideal generated by
![]() $P_1$
and
$P_1$
and
![]() $P_2$
is not prime. Thus, it is not clear whether a bound for Theorem 1.1 would imply a bound for Theorem 1.2. The latter problem was open, prior to this work, for any degree
$P_2$
is not prime. Thus, it is not clear whether a bound for Theorem 1.1 would imply a bound for Theorem 1.2. The latter problem was open, prior to this work, for any degree
![]() $r> 1$
.
$r> 1$
.
The Sylvester–Gallai theorem has important consequences for locally decodable and locally correctable codes [Reference Barak, Dvir, Wigderson and Yehudayoff1, Reference Dvir, Saraf and Wigderson8], for reconstruction of certain depth-
![]() $3$
circuits [Reference Shpilka19, Reference Karnin and Shpilka14, Reference Sinha and Raz21] and for the polynomial identity testing (PIT for short) problem, which was the main motivation for Gupta [Reference Gupta12]. While a solution to Problem 1.1 would not yield new PIT algorithms, the following ‘colored’ version of it would [Reference Beecken, Mittmann and Saxena2, Reference Gupta12].
$3$
circuits [Reference Shpilka19, Reference Karnin and Shpilka14, Reference Sinha and Raz21] and for the polynomial identity testing (PIT for short) problem, which was the main motivation for Gupta [Reference Gupta12]. While a solution to Problem 1.1 would not yield new PIT algorithms, the following ‘colored’ version of it would [Reference Beecken, Mittmann and Saxena2, Reference Gupta12].
Conjecture 1.3 (Conjecture 30 of [Reference Gupta12]).
There is a function
![]() $\lambda :\mathbb {N}\to \mathbb {N}$
such that the following holds for every
$\lambda :\mathbb {N}\to \mathbb {N}$
such that the following holds for every
![]() $r,n\in \mathbb {N}$
. Let
$r,n\in \mathbb {N}$
. Let
![]() $R, B, G$
be finite disjoint sets of pairwise linearly independent, irreducible, homogeneous polynomials in
$R, B, G$
be finite disjoint sets of pairwise linearly independent, irreducible, homogeneous polynomials in
![]() $\mathbb {C}[x_1,\ldots ,x_n]$
of degree
$\mathbb {C}[x_1,\ldots ,x_n]$
of degree
![]() $\leq r$
such that for every pair
$\leq r$
such that for every pair
![]() $Q_1,Q_2$
from distinct sets it holds that, whenever both
$Q_1,Q_2$
from distinct sets it holds that, whenever both
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
vanish, then so does the product of all the polynomials in the third set. Then, the algebraic rank of
$Q_2$
vanish, then so does the product of all the polynomials in the third set. Then, the algebraic rank of
![]() $(R \cup B \cup G)$
is at most
$(R \cup B \cup G)$
is at most
![]() $\lambda (r)$
.
$\lambda (r)$
.
1.1 Subsequent work
In [Reference Peleg and Shpilka17], we gave a positive answer to Conjecture 1.3 for the case of degree-
![]() $2$
polynomials (
$2$
polynomials (
![]() $r=2$
). This implied the first polynomial time PIT algorithm for depth-
$r=2$
). This implied the first polynomial time PIT algorithm for depth-
![]() $4$
circuits with quadratic polynomials at the bottom (see [Reference Peleg and Shpilka17] for a definition). While we do not know whether Conjecture 1.3 or Problem 1.1 imply the other, the proof technique in [Reference Peleg and Shpilka17] is greatly influenced by the proof in this paper, and in particular, Theorem 1.5 played an important role in [Reference Peleg and Shpilka17].
$4$
circuits with quadratic polynomials at the bottom (see [Reference Peleg and Shpilka17] for a definition). While we do not know whether Conjecture 1.3 or Problem 1.1 imply the other, the proof technique in [Reference Peleg and Shpilka17] is greatly influenced by the proof in this paper, and in particular, Theorem 1.5 played an important role in [Reference Peleg and Shpilka17].
In [Reference Peleg, Shpilka, Goaoc and Kerber18, Reference Garg, Oliveira and Sengupta11] a robust version of [Reference Shpilka20] was obtained, that is, a robust version of Theorem 1.1 for the case
![]() $r=2$
was proved.
$r=2$
was proved.
1.2 Our result
Our main result gives a bound on the linear dimension of homogeneous polynomials satisfying the conditions of Theorem 1.2 when all the polynomials are irreducible of degree at most
![]() $2$
. Specifically, we prove the following theorem.
$2$
. Specifically, we prove the following theorem.
Theorem 1.4. There exists a universal constant c such that the following holds. Let
![]() ${{\mathcal {Q}}} = \{Q_i\}_{i\in \{1,\ldots ,m\}}\subset \mathbb {C}[x_1,\ldots ,x_n]$
be a finite set of pairwise linearly independent homogeneous quadratic polynomials such that every
${{\mathcal {Q}}} = \{Q_i\}_{i\in \{1,\ldots ,m\}}\subset \mathbb {C}[x_1,\ldots ,x_n]$
be a finite set of pairwise linearly independent homogeneous quadratic polynomials such that every
![]() $Q_i\in {{\mathcal {Q}}}$
is either irreducible or a square of a linear form. Assume that, for every
$Q_i\in {{\mathcal {Q}}}$
is either irreducible or a square of a linear form. Assume that, for every
![]() $i\neq j$
, whenever
$i\neq j$
, whenever
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
vanish, then so does
$Q_j$
vanish, then so does
![]() $\prod _{k\in \{1,\ldots ,m\} \setminus \{i,j\}} Q_k$
. Then,
$\prod _{k\in \{1,\ldots ,m\} \setminus \{i,j\}} Q_k$
. Then,
![]() $\dim (\operatorname {span}\{{{{\mathcal {Q}}}}\})\leq c$
.
$\dim (\operatorname {span}\{{{{\mathcal {Q}}}}\})\leq c$
.
An interesting aspect of our result is that, while the conjectures of [Reference Beecken, Mittmann and Saxena2, Reference Gupta12] speak about the algebraic rank, we prove a stronger result that bounds the linear dimension (the linear rank is an upper bound on the algebraic rank). As our proof is quite technical, it is an interesting question whether one could simplify our arguments by arguing directly about the algebraic rank.
An important algebraic tool in the proof of Theorem 1.4 is the following result characterizing the different cases in which a product of quadratic polynomials vanishes whenever two other quadratics vanish.
Theorem 1.5. Let
![]() $\{Q_k\}_{k\in {\mathcal {K}}},A$
and B be n-variate, homogeneous, quadratic polynomials, over
$\{Q_k\}_{k\in {\mathcal {K}}},A$
and B be n-variate, homogeneous, quadratic polynomials, over
![]() $\mathbb {C}$
, satisfying that, whenever A and B vanish, then so does
$\mathbb {C}$
, satisfying that, whenever A and B vanish, then so does
![]() $\prod _{k\in {\mathcal {K}}} Q_k$
. Then, one of the following cases must hold:
$\prod _{k\in {\mathcal {K}}} Q_k$
. Then, one of the following cases must hold:
-
(prime-case): There is
 $k\in {\mathcal {K}}$
such that
$k\in {\mathcal {K}}$
such that
 $Q_k$
is in the linear span of A and B.
$Q_k$
is in the linear span of A and B. -
(product-case): There exists a nontrivial linear combination of the form
 $\alpha A+\beta B = ab$
, where a and b are linear forms.
$\alpha A+\beta B = ab$
, where a and b are linear forms. -
(linear-case): There exist two linear forms a and b such that when setting
 $a=b=0$
we get that A and B vanish.
$a=b=0$
we get that A and B vanish.
The statement of the result is quite similar to Theorem 1.8 of [Reference Shpilka20] that proved a similar result when
![]() $|{\mathcal {K}}|=1$
. Specifically, in [Reference Shpilka20] the second item reads ‘There exists a non trivial linear combination of the form
$|{\mathcal {K}}|=1$
. Specifically, in [Reference Shpilka20] the second item reads ‘There exists a non trivial linear combination of the form
![]() $\alpha A+\beta B = a^2$
, where a is a linear form.’ This difference in the statements (which is necessary) is also responsible for the harder work we do in the paper.
$\alpha A+\beta B = a^2$
, where a is a linear form.’ This difference in the statements (which is necessary) is also responsible for the harder work we do in the paper.
It was pointed out by Rafael Mendes de Oliveira and by one of the reviewers that a more general statement of Theorem 1.5 was obtained in [Reference Colliot-Thélène, Sansuc and Swinnerton-Dyer5, Section 1] and [Reference Vallance, Hodge and Pedoe13, Chapter XIII]. We discuss the similarities and differences from our theorem in subsection 1.5.
1.3 Proof idea
Our proof has a similar structure to the proofs in [Reference Shpilka20], but it does not rely on any of the results proved there.
Our starting point is the observation that Theorem 1.5 guarantees that unless one of
![]() $\{Q_k\}$
is in the linear span of A and B then A and B must satisfy a very strong property, namely, they must span a reducible quadratic or they have a very low rank (as quadratic polynomials). The proof of this theorem is based on analyzing the resultant of A and B with respect to some variable. We now explain how this theorem can be used to prove Theorem 1.4.
$\{Q_k\}$
is in the linear span of A and B then A and B must satisfy a very strong property, namely, they must span a reducible quadratic or they have a very low rank (as quadratic polynomials). The proof of this theorem is based on analyzing the resultant of A and B with respect to some variable. We now explain how this theorem can be used to prove Theorem 1.4.
Consider a set of polynomials
![]() ${\mathcal {Q}}=\{{Q}_1,\ldots , {Q}_{m}\}$
satisfying the condition of Theorem 1.4. First, consider the case in which for every
${\mathcal {Q}}=\{{Q}_1,\ldots , {Q}_{m}\}$
satisfying the condition of Theorem 1.4. First, consider the case in which for every
![]() $Q\in {\mathcal {Q}}$
, at least, say,
$Q\in {\mathcal {Q}}$
, at least, say,
![]() $(1/100)\cdot m$
of the polynomials
$(1/100)\cdot m$
of the polynomials
![]() $Q_i\in {\mathcal {Q}}$
, satisfy that there is another polynomial in
$Q_i\in {\mathcal {Q}}$
, satisfy that there is another polynomial in
![]() ${\mathcal {Q}}$
in
${\mathcal {Q}}$
in
![]() $\operatorname {span}\{{Q,Q_i}\}$
. In this case, we can use the robust version of the Sylvester–Gallai theorem [Reference Barak, Dvir, Wigderson and Yehudayoff1, Reference Dvir, Saraf and Wigderson8] (see Theorem 2.7) to deduce that the linear dimension of
$\operatorname {span}\{{Q,Q_i}\}$
. In this case, we can use the robust version of the Sylvester–Gallai theorem [Reference Barak, Dvir, Wigderson and Yehudayoff1, Reference Dvir, Saraf and Wigderson8] (see Theorem 2.7) to deduce that the linear dimension of
![]() ${\mathcal {Q}}$
is small.
${\mathcal {Q}}$
is small.
The second case we consider is when every polynomial
![]() $Q\in {\mathcal {Q}}$
that did not satisfy the first case now satisfies that for at least, say,
$Q\in {\mathcal {Q}}$
that did not satisfy the first case now satisfies that for at least, say,
![]() $(1/100)\cdot m$
of the polynomials
$(1/100)\cdot m$
of the polynomials
![]() $Q_i\in {\mathcal {Q}}$
, there are linear forms
$Q_i\in {\mathcal {Q}}$
, there are linear forms
![]() $a_i$
and
$a_i$
and
![]() $b_i$
such that
$b_i$
such that
![]() $Q,Q_i \in \left \langle {a_i,b_i}\right \rangle $
. We prove that, if this is the case, then there is a bounded dimensional linear space of linear forms, V such that all the polynomials in
$Q,Q_i \in \left \langle {a_i,b_i}\right \rangle $
. We prove that, if this is the case, then there is a bounded dimensional linear space of linear forms, V such that all the polynomials in
![]() ${\mathcal {Q}}$
that are of rank
${\mathcal {Q}}$
that are of rank
![]() $2$
are in
$2$
are in
![]() $\left \langle {V}\right \rangle $
. Then we argue that the polynomials that are not in
$\left \langle {V}\right \rangle $
. Then we argue that the polynomials that are not in
![]() $\left \langle {V}\right \rangle $
satisfy the robust version of the Sylvester–Gallai theorem (Theorem 2.7). Finally, we bound the dimension of
$\left \langle {V}\right \rangle $
satisfy the robust version of the Sylvester–Gallai theorem (Theorem 2.7). Finally, we bound the dimension of
![]() ${\mathcal {Q}} \cap \left \langle {V}\right \rangle $
.
${\mathcal {Q}} \cap \left \langle {V}\right \rangle $
.
Most of the work, however, (section 5) goes into studying what happens in the remaining case when there is some polynomial
![]() $Q_o\in {\mathcal {Q}}$
for which at least
$Q_o\in {\mathcal {Q}}$
for which at least
![]() $0.98m$
of the other polynomials in
$0.98m$
of the other polynomials in
![]() ${\mathcal {Q}}$
satisfy Theorem 1.5(product-case) with
${\mathcal {Q}}$
satisfy Theorem 1.5(product-case) with
![]() $Q_o$
. This puts a strong restriction on the structure of these
$Q_o$
. This puts a strong restriction on the structure of these
![]() $0.98m$
polynomials. Specifically, each of them is of the form
$0.98m$
polynomials. Specifically, each of them is of the form
![]() $Q_i = Q_o+a_ib_i$
, where
$Q_i = Q_o+a_ib_i$
, where
![]() $a_i$
and
$a_i$
and
![]() $b_i$
are linear forms. The idea in this case is to show that the set
$b_i$
are linear forms. The idea in this case is to show that the set
![]() $\{a_i,b_i\}$
is of low dimension. This is done by again studying the consequences of Theorem 1.5 for pairs of polynomials
$\{a_i,b_i\}$
is of low dimension. This is done by again studying the consequences of Theorem 1.5 for pairs of polynomials
![]() $Q_o+a_ib_i,Q_o+a_jb_j\in {\mathcal {Q}}$
. After bounding the dimension of these
$Q_o+a_ib_i,Q_o+a_jb_j\in {\mathcal {Q}}$
. After bounding the dimension of these
![]() $0.98m$
polynomials, we bound the dimension of all the polynomials in
$0.98m$
polynomials, we bound the dimension of all the polynomials in
![]() ${\mathcal {Q}}$
. The proof of this case is more involved than the cases described earlier. An outline of the proof is described in section 5.
${\mathcal {Q}}$
. The proof of this case is more involved than the cases described earlier. An outline of the proof is described in section 5.
1.4 On the relation to the proof of [Reference Shpilka20]
In [Reference Shpilka20], the following theorem was proved.
Theorem 1.6 (Theorem 1.7 of [Reference Shpilka20]).
Let
![]() $\{Q_i\}_{i\in [m]}$
be homogeneous quadratic polynomials over
$\{Q_i\}_{i\in [m]}$
be homogeneous quadratic polynomials over
![]() $\mathbb {C}$
such that each
$\mathbb {C}$
such that each
![]() $Q_i$
is either irreducible or a square of a linear function. Assume further that for every
$Q_i$
is either irreducible or a square of a linear function. Assume further that for every
![]() $i\neq j$
there exists
$i\neq j$
there exists
![]() $k\not \in \{i,j\}$
such that whenever
$k\not \in \{i,j\}$
such that whenever
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
vanish
$Q_j$
vanish
![]() $Q_k$
vanishes as well. Then the linear span of the
$Q_k$
vanishes as well. Then the linear span of the
![]() $Q_i$
’s has dimension
$Q_i$
’s has dimension
![]() $O(1)$
.
$O(1)$
.
As mentioned earlier, the steps in our proof are similar to the proof of Theorem 1.7 in [Reference Shpilka20]. Specifically, [Reference Shpilka20] also relies on an analog of Theorem 1.5 and divides the proof according to whether all polynomials satisfy the first case above (in our terminology, the prime case) or not. However, the fact that Theorem 1.5(product-case) is different than the corresponding case in the statement of Theorem 1.8 of [Reference Shpilka20] makes our proof significantly more difficult. The reason for this is that, while in [Reference Shpilka20] we could always pinpoint which polynomial vanishes when
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
vanish, here, we only know that this polynomial belongs to a small set of polynomials. This leads to a richer structure in Theorem 1.5 and consequently to a considerably more complicated proof. To understand the effect of this on our proof, we note that the case corresponding to Theorem 1.5(product-case) was the simpler case to analyze in the proof of [Reference Shpilka20]. The fact that
$Q_j$
vanish, here, we only know that this polynomial belongs to a small set of polynomials. This leads to a richer structure in Theorem 1.5 and consequently to a considerably more complicated proof. To understand the effect of this on our proof, we note that the case corresponding to Theorem 1.5(product-case) was the simpler case to analyze in the proof of [Reference Shpilka20]. The fact that
![]() $a_i=b_i$
when
$a_i=b_i$
when
![]() $|{\mathcal {K}}|=1$
almost immediately implied that the dimension of the span of the
$|{\mathcal {K}}|=1$
almost immediately implied that the dimension of the span of the
![]() $a_i$
s is constant (see Claim 5.2 in [Reference Shpilka20]). In our case, however, this is the bulk of the proof, and section 5 is devoted to handling this case.
$a_i$
s is constant (see Claim 5.2 in [Reference Shpilka20]). In our case, however, this is the bulk of the proof, and section 5 is devoted to handling this case.
In addition to being technically more challenging, our proof gives new insights that may be extended to higher-degree polynomials. The first is Theorem 1.5, which extends a similar theorem that was proved for the simpler setting of [Reference Shpilka20]. Our second contribution is that we show (more or less) that either the polynomials in our set satisfy the robust version of the Sylvester–Gallai theorem (Theorem 2.6) or the linear functions composing the polynomials satisfy the theorem. Potentially, this may be extended to higher-degree polynomials.
1.5 The structure theorem
As mentioned above, Rafael Mendes de Oliveira and an anonymous referee turned our attention to [Reference Colliot-Thélène, Sansuc and Swinnerton-Dyer5, Section 1] and [Reference Vallance, Hodge and Pedoe13, Chapter XIII]. Both classify ideals generated by two quadratics, a result that is more general than what we prove in Theorem 1.5. Nevertheless, Theorem 1.5 is enough for us to obtain our results, and it has the added advantage that its proof is elementary.
Specifically, [Reference Colliot-Thélène, Sansuc and Swinnerton-Dyer5, Lemma 1.3] corresponds to the case where the ideal
![]() $\left \langle {A,B}\right \rangle $
is prime, which is covered in our Theorem 1.5(prime-case).
$\left \langle {A,B}\right \rangle $
is prime, which is covered in our Theorem 1.5(prime-case).
Theorem 1.5(product-case) was studied in Lemmata 1.6, 1.7 and 1.10 in [Reference Colliot-Thélène, Sansuc and Swinnerton-Dyer5]. For example, the subspace
![]() $H_1,H_2$
in Lemma 1.6 is the set of zeros of a and b from Theorem 1.5(product-case) and the rank-
$H_1,H_2$
in Lemma 1.6 is the set of zeros of a and b from Theorem 1.5(product-case) and the rank-
![]() $2$
form of Lemma 1.7 is
$2$
form of Lemma 1.7 is
![]() $ab$
. Lemma 1.10 covers the case
$ab$
. Lemma 1.10 covers the case
![]() $a=b$
.
$a=b$
.
Lemmata 1.2 and 1.4 in [Reference Colliot-Thélène, Sansuc and Swinnerton-Dyer5] correspond to the case where the ideal is contained in a linear subspace of codimension
![]() $2$
, which is covered in our Theorem 1.5(linear-case).
$2$
, which is covered in our Theorem 1.5(linear-case).
The proofs in [Reference Colliot-Thélène, Sansuc and Swinnerton-Dyer5] rely on cycle decomposition of the variety
![]() $\{{\boldsymbol {\alpha }}\in \mathbb {C}^n \mid A({\boldsymbol {\alpha }})=B({\boldsymbol {\alpha }})=0\}$
, while our proof only relies on simple properties of the resultant.
$\{{\boldsymbol {\alpha }}\in \mathbb {C}^n \mid A({\boldsymbol {\alpha }})=B({\boldsymbol {\alpha }})=0\}$
, while our proof only relies on simple properties of the resultant.
1.6 Organization
The paper is organized as follows. section 2 contains basic facts regarding the resultant and some other tools and notation used in this work. section 3 contains the proof of our structure theorem (Theorem 1.5). In section 4, we give the proof of Theorem 1.4. This proof uses a main theorem which will be proved in section 5. Finally, in section 6, we discuss further directions and open problems.
2 Preliminaries
In this section, we explain our notation and present some basic algebraic preliminaries.
We will use the following notation. Greek letters
![]() $\alpha , \beta ,\ldots $
denote scalars from
$\alpha , \beta ,\ldots $
denote scalars from
![]() $\mathbb {C}$
. Noncapitalized letters
$\mathbb {C}$
. Noncapitalized letters
![]() $a,b,c,\ldots $
denote linear forms and
$a,b,c,\ldots $
denote linear forms and
![]() $x,y,z$
denote variables (which are also linear forms). Bold-faced letters denote vectors, for example,
$x,y,z$
denote variables (which are also linear forms). Bold-faced letters denote vectors, for example,
![]() ${\mathbf {x}} = (x_1,\ldots ,x_n)$
denotes a vector of variables,
${\mathbf {x}} = (x_1,\ldots ,x_n)$
denotes a vector of variables,
![]() ${\boldsymbol {\alpha }}=(\alpha _1,\ldots ,\alpha _n)$
is a vector of scalars and
${\boldsymbol {\alpha }}=(\alpha _1,\ldots ,\alpha _n)$
is a vector of scalars and
![]() ${\mathbf {0}} = (0,\ldots ,0)$
the zero vector. We sometimes do not use a boldface notation for a point in a vector space if we do not use its structure as a vector. Capital letters such as
${\mathbf {0}} = (0,\ldots ,0)$
the zero vector. We sometimes do not use a boldface notation for a point in a vector space if we do not use its structure as a vector. Capital letters such as
![]() $A,Q,P$
denote quadratic polynomials whereas
$A,Q,P$
denote quadratic polynomials whereas
![]() $V,U,W$
denote linear spaces. Calligraphic letters
$V,U,W$
denote linear spaces. Calligraphic letters
![]() $\cal I,J,F,Q,T$
denote sets. For a positive integer n, we denote
$\cal I,J,F,Q,T$
denote sets. For a positive integer n, we denote
![]() $[n]=\{1,2,\ldots ,n\}$
. For a matrix X, we denote by
$[n]=\{1,2,\ldots ,n\}$
. For a matrix X, we denote by
![]() $|X|$
the determinant of X.
$|X|$
the determinant of X.
A commutative ring is a ring in which the multiplication operation is commutative. We mainly use the multivariate polynomial ring,
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
. An Ideal
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
. An Ideal
![]() $I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
is an additive subgroup that is closed under multiplication by ring elements. For
$I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
is an additive subgroup that is closed under multiplication by ring elements. For
![]() ${\mathcal {S}} \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
, we denote with
${\mathcal {S}} \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
, we denote with
![]() $\left \langle {{\mathcal {S}}}\right \rangle $
the ideal generated by
$\left \langle {{\mathcal {S}}}\right \rangle $
the ideal generated by
![]() ${\mathcal {S}}$
, that is, the smallest ideal that contains
${\mathcal {S}}$
, that is, the smallest ideal that contains
![]() ${\mathcal {S}}$
. For example, for two polynomials
${\mathcal {S}}$
. For example, for two polynomials
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
, the ideal
$Q_2$
, the ideal
![]() $\left \langle {Q_1,Q_2}\right \rangle $
is the set
$\left \langle {Q_1,Q_2}\right \rangle $
is the set
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]Q_1 + \mathbb {C}[ {x}_1,\ldots , {x}_{n}]Q_2$
. For a linear subspace V, we have that
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}]Q_1 + \mathbb {C}[ {x}_1,\ldots , {x}_{n}]Q_2$
. For a linear subspace V, we have that
![]() $\left \langle {V}\right \rangle $
is the ideal generated by any basis of V. The radical of an ideal I, denoted by
$\left \langle {V}\right \rangle $
is the ideal generated by any basis of V. The radical of an ideal I, denoted by
![]() $\sqrt {I}$
, is the set of all ring elements, r, satisfying that for some natural number m (that may depend on r),
$\sqrt {I}$
, is the set of all ring elements, r, satisfying that for some natural number m (that may depend on r),
![]() $r^m \in I$
. Hilbert’s Nullstellensatz implies that, in
$r^m \in I$
. Hilbert’s Nullstellensatz implies that, in
![]() $\mathbb {C}[x_1,\ldots ,x_n]$
, if a polynomial Q vanishes whenever
$\mathbb {C}[x_1,\ldots ,x_n]$
, if a polynomial Q vanishes whenever
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
vanish, then
$Q_2$
vanish, then
![]() $Q\in \sqrt {\left \langle {Q_1,Q_2}\right \rangle }$
(see, e.g., [Reference Cox, Little and O’Shea6]). We shall often use the notation
$Q\in \sqrt {\left \langle {Q_1,Q_2}\right \rangle }$
(see, e.g., [Reference Cox, Little and O’Shea6]). We shall often use the notation
![]() $Q\in \sqrt {\left \langle {Q_1,Q_2}\right \rangle }$
to denote this vanishing condition. For an ideal
$Q\in \sqrt {\left \langle {Q_1,Q_2}\right \rangle }$
to denote this vanishing condition. For an ideal
![]() $I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
, we denote by
$I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
, we denote by
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}] /I$
the quotient ring, that is, the ring whose elements are the cosets of I in
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}] /I$
the quotient ring, that is, the ring whose elements are the cosets of I in
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
with the proper multiplication and addition operations. For an ideal
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
with the proper multiplication and addition operations. For an ideal
![]() $I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
, we denote the set of all common zeros of elements of I by
$I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
, we denote the set of all common zeros of elements of I by
![]() $Z(I)$
.
$Z(I)$
.
For
![]() $V_1,\ldots ,V_k$
linear spaces, we use
$V_1,\ldots ,V_k$
linear spaces, we use
![]() $\sum _{i=1}^k V_i$
to denote the linear space
$\sum _{i=1}^k V_i$
to denote the linear space
![]() $V_1 + \ldots + V_k$
. For two nonzero polynomials A and B, we denote
$V_1 + \ldots + V_k$
. For two nonzero polynomials A and B, we denote
![]() $A\sim B$
if
$A\sim B$
if
![]() $B \in \operatorname {span}\{{A}\}$
. For a space of linear forms
$B \in \operatorname {span}\{{A}\}$
. For a space of linear forms
![]() ${V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}}$
, we say that a polynomial
${V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}}$
, we say that a polynomial
![]() $P \in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
depends only on V if the value of P is determined by the values of the linear forms
$P \in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
depends only on V if the value of P is determined by the values of the linear forms
![]() $v_1,\ldots ,v_{\Delta }$
. More formally, we say that P depends only on V if there is a
$v_1,\ldots ,v_{\Delta }$
. More formally, we say that P depends only on V if there is a
![]() $\Delta $
-variate polynomial
$\Delta $
-variate polynomial
![]() $\tilde {P}$
such that
$\tilde {P}$
such that
![]() $P \equiv \tilde {P}(v_1,\ldots ,v_{\Delta })$
. We denote by
$P \equiv \tilde {P}(v_1,\ldots ,v_{\Delta })$
. We denote by
![]() $\mathbb {C}[V]=\mathbb {C}[ {v}_1,\ldots , {v}_{\Delta }]\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
the subring of polynomials that depend only on V.
$\mathbb {C}[V]=\mathbb {C}[ {v}_1,\ldots , {v}_{\Delta }]\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
the subring of polynomials that depend only on V.
Another notation that we will use throughout the proof is congruence modulo linear forms.
Definition 2.1. Let
![]() $V\subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be a space of linear forms, and
$V\subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be a space of linear forms, and
![]() $P,Q\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
. We say that
$P,Q\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
. We say that
![]() $P\equiv _V Q$
if
$P\equiv _V Q$
if
![]() $P-Q \in \left \langle {V}\right \rangle $
.
$P-Q \in \left \langle {V}\right \rangle $
.
Fact 2.2. Let
![]() $V\subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be a space of linear forms and
$V\subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be a space of linear forms and
![]() $P,Q\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
. If
$P,Q\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
. If
![]() $P = \prod _{k=1}^t P_k$
and
$P = \prod _{k=1}^t P_k$
and
![]() $Q = \prod _{k=1}^t Q_k$
satisfy that, for all k,
$Q = \prod _{k=1}^t Q_k$
satisfy that, for all k,
![]() $P_k$
and
$P_k$
and
![]() $Q_k$
are irreducible in
$Q_k$
are irreducible in
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]/{\langle V\rangle }$
, and
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}]/{\langle V\rangle }$
, and
![]() $P \equiv _V Q \not \equiv _V 0$
, then, up to a permutation of the indices and multiplication by scalars,
$P \equiv _V Q \not \equiv _V 0$
, then, up to a permutation of the indices and multiplication by scalars,
![]() $P_k\equiv _V Q_k$
for all
$P_k\equiv _V Q_k$
for all
![]() $k\in [t]$
.
$k\in [t]$
.
This follows from the fact that the quotient ring
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]/{\langle V\rangle }$
is a unique factorization domain.
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}]/{\langle V\rangle }$
is a unique factorization domain.
2.1 Sylvester–Gallai theorem and some of its variants
In this section, we present the formal statement of the Sylvester–Gallai theorem and the extensions that we use in this work.
Definition 2.3. Given a set of points,
![]() $v_1,\ldots ,v_m$
, we call a line that passes through exactly two of the points of the set an ordinary line.
$v_1,\ldots ,v_m$
, we call a line that passes through exactly two of the points of the set an ordinary line.
Theorem 2.4 (Sylvester–Gallai theorem [Reference Melchior16, Reference Gallai10]).
If m distinct points
![]() $v_1,\ldots ,v_m$
in
$v_1,\ldots ,v_m$
in
![]() $\mathbb {R}^n$
are not colinear, then they define at least one ordinary line.
$\mathbb {R}^n$
are not colinear, then they define at least one ordinary line.
Theorem 2.5 (Kelly’s theorem [Reference Kelly15]).
If m distinct points
![]() $v_1,\ldots ,v_m$
in
$v_1,\ldots ,v_m$
in
![]() $\mathbb {C}^n$
are not coplanar, then they define at least one ordinary line.
$\mathbb {C}^n$
are not coplanar, then they define at least one ordinary line.
The robust version of the theorem was stated and proved in [Reference Barak, Dvir, Wigderson and Yehudayoff1, Reference Dvir, Saraf and Wigderson8].
Definition 2.6. We say that a finite set of points
![]() $\{v_1,\ldots ,v_m\}\subset \mathbb {C}^n$
is an
$\{v_1,\ldots ,v_m\}\subset \mathbb {C}^n$
is an
![]() $\delta $
-SG configuration if for every
$\delta $
-SG configuration if for every
![]() $i\in [m]$
there exists at least
$i\in [m]$
there exists at least
![]() $\delta m$
values of
$\delta m$
values of
![]() $j \in [m]$
such that the line through
$j \in [m]$
such that the line through
![]() $v_i,v_j$
is not ordinary.
$v_i,v_j$
is not ordinary.
Theorem 2.7 (Robust Sylvester–Gallai theorem, Theorem
 $1.9$
of [Reference Dvir, Saraf and Wigderson8]).
$1.9$
of [Reference Dvir, Saraf and Wigderson8]).
Let
![]() $V = \lbrace v_1,\ldots ,v_m\rbrace \subset \mathbb {C}^n$
be a
$V = \lbrace v_1,\ldots ,v_m\rbrace \subset \mathbb {C}^n$
be a
![]() $\delta $
-SG configuration. Then
$\delta $
-SG configuration. Then
![]() $\dim (\operatorname {span}\{{v_1,\ldots ,v_m}\}) \leq \frac {12}{\delta }+1$
.
$\dim (\operatorname {span}\{{v_1,\ldots ,v_m}\}) \leq \frac {12}{\delta }+1$
.
The following is the colored version of the Sylvester–Gallai theorem.
Theorem 2.8 (Theorem
 $3$
of [Reference Edelstein and Kelly9]).
$3$
of [Reference Edelstein and Kelly9]).
Let
![]() ${\mathcal {T}}_i$
, for
${\mathcal {T}}_i$
, for
![]() $i\in [3]$
, be disjoint finite subsets of
$i\in [3]$
, be disjoint finite subsets of
![]() $\mathbb {C}^n$
such that for every
$\mathbb {C}^n$
such that for every
![]() $i\neq j$
and any two points
$i\neq j$
and any two points
![]() $p_1\in {\mathcal {T}}_i$
and
$p_1\in {\mathcal {T}}_i$
and
![]() $p_2 \in {\mathcal {T}}_j$
there exists a point
$p_2 \in {\mathcal {T}}_j$
there exists a point
![]() $p_3$
in the third set that lies on the line passing through
$p_3$
in the third set that lies on the line passing through
![]() $p_1$
and
$p_1$
and
![]() $p_2$
. Then, any such
$p_2$
. Then, any such
![]() $\{{\mathcal {T}}_i\}$
satisfy that
$\{{\mathcal {T}}_i\}$
satisfy that
![]() $\dim (\operatorname {span}\{{\cup _i {\mathcal {T}}_i}\})\leq 3$
.
$\dim (\operatorname {span}\{{\cup _i {\mathcal {T}}_i}\})\leq 3$
.
We also state the equivalent algebraic versions of the Sylvester–Gallai theorem.
Theorem 2.9. Let
![]() ${\mathcal {S}} = \lbrace {\mathbf {s}}_1,\ldots ,{\mathbf {s}}_m\rbrace \subset \mathbb {C}^n$
be a set of pairwise linearly independent vectors such that for every
${\mathcal {S}} = \lbrace {\mathbf {s}}_1,\ldots ,{\mathbf {s}}_m\rbrace \subset \mathbb {C}^n$
be a set of pairwise linearly independent vectors such that for every
![]() $i\neq j\in [m]$
there is a distinct
$i\neq j\in [m]$
there is a distinct
![]() $k \in [m]$
for which
$k \in [m]$
for which
![]() ${\mathbf {s}}_k \in \operatorname {span}\{{{\mathbf {s}}_i,{\mathbf {s}}_j}\}$
. Then
${\mathbf {s}}_k \in \operatorname {span}\{{{\mathbf {s}}_i,{\mathbf {s}}_j}\}$
. Then
![]() $\dim ({\mathcal {S}}) \leq 3$
.
$\dim ({\mathcal {S}}) \leq 3$
.
Theorem 2.10. Let
![]() ${\mathcal {P}} = \lbrace \ell _1,\ldots ,\ell _m\rbrace \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be a set of pairwise linearly independent linear forms such that for every
${\mathcal {P}} = \lbrace \ell _1,\ldots ,\ell _m\rbrace \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be a set of pairwise linearly independent linear forms such that for every
![]() $i\neq j\in [m]$
there is a distinct
$i\neq j\in [m]$
there is a distinct
![]() $k \in [m]$
for which whenever
$k \in [m]$
for which whenever
![]() $\ell _i, \ell _j$
vanish so does
$\ell _i, \ell _j$
vanish so does
![]() $\ell _k$
. Then
$\ell _k$
. Then
![]() $\dim ({\mathcal {P}}) \leq 3$
.
$\dim ({\mathcal {P}}) \leq 3$
.
In this paper, we refer to each of Theorem 2.5, Theorem 2.9 and Theorem 2.10 as the Sylvester–Gallai theorem. We shall also refer to sets of points/vectors/linear forms that satisfy the conditions of the relevant theorem as satisfying the condition of the Sylvester–Gallai theorem.
2.2 Resultant
A tool that will play an important role in the proof of Theorem 1.5 is the resultant of two polynomials. We will only define the resultant of a quadratic polynomial and a linear polynomial as this is the case relevant to our work.Footnote
1
Let
![]() $A,B\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
. View A and B as polynomials in
$A,B\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
. View A and B as polynomials in
![]() $x_1$
over
$x_1$
over
![]() $\mathbb {C}[x_2,\ldots ,x_n]$
, and assume that
$\mathbb {C}[x_2,\ldots ,x_n]$
, and assume that
![]() $\deg _{x_1}(A) = 2 $
and
$\deg _{x_1}(A) = 2 $
and
![]() $\deg _{x_1}(B) = 1 $
, namely,
$\deg _{x_1}(B) = 1 $
, namely,
Then, the resultant of A and B with respect to
![]() $x_1$
is the determinant of their Sylvester matrix
$x_1$
is the determinant of their Sylvester matrix
 $$ \begin{align*} \mathrm{Res}_{x_1}(A,B) := \left| \begin{bmatrix} A_0 & B_0 & 0 \\ a & b & B_0 \\ \alpha & 0 & b \\ \end{bmatrix}\right| . \end{align*} $$
$$ \begin{align*} \mathrm{Res}_{x_1}(A,B) := \left| \begin{bmatrix} A_0 & B_0 & 0 \\ a & b & B_0 \\ \alpha & 0 & b \\ \end{bmatrix}\right| . \end{align*} $$
A useful fact is that, if the resultant of A and B vanishes, then they share a common factor.
Theorem 2.11 (See, for example, Proposition 8 in $5 of Chapter 3 in [Reference Cox, Little and O’Shea6]).
Given
![]() $F,G\in \mathbb {F}[{x}_1,\ldots , {x}_{n}]$
of positive degree in
$F,G\in \mathbb {F}[{x}_1,\ldots , {x}_{n}]$
of positive degree in
![]() $x_1$
, the resultant
$x_1$
, the resultant
![]() $\mathrm {Res}_{x_1}(F,G)$
is an integer polynomial in the coefficients of F and G. Furthermore, F and G have a common factor in
$\mathrm {Res}_{x_1}(F,G)$
is an integer polynomial in the coefficients of F and G. Furthermore, F and G have a common factor in
![]() $\mathbb {F}[{x}_1,\ldots , {x}_{n}]$
if and only if
$\mathbb {F}[{x}_1,\ldots , {x}_{n}]$
if and only if
![]() $\mathrm {Res}_{x_1}(F,G) = 0$
.
$\mathrm {Res}_{x_1}(F,G) = 0$
.
2.3 Rank of quadratic polynomials
In this section, we define the rank of a quadratic polynomial and present some of its useful properties.
Definition 2.12. For a homogeneous quadratic polynomial Q, we denote with
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q)$
the minimal r such that there are
$\operatorname {\mathrm {rank}}_{\text {s}}(Q)$
the minimal r such that there are
![]() $2r$
linear forms
$2r$
linear forms
![]() $\{a_k\}_{k=1}^{2r}$
satisfying
$\{a_k\}_{k=1}^{2r}$
satisfying
![]() $Q=\sum _{k=1}^r a_{2k}\cdot a_{2k-1}$
. We call such representation a minimal representation of Q.
$Q=\sum _{k=1}^r a_{2k}\cdot a_{2k-1}$
. We call such representation a minimal representation of Q.
This is a slightly different definition than the usual way one defines rank of quadratic forms,Footnote
2
but it is more suitable for our needs. We note that a quadratic Q is irreducible if and only if
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q)>1$
. The next claim shows that a minimal representation is unique in the sense that the space spanned by the linear forms in it is unique.
$\operatorname {\mathrm {rank}}_{\text {s}}(Q)>1$
. The next claim shows that a minimal representation is unique in the sense that the space spanned by the linear forms in it is unique.
Claim 2.13. Let Q be a homogeneous quadratic polynomial, and let
![]() $Q=\sum _{i=1}^{r}a_{2i-1}\cdot a_{2i}$
and
$Q=\sum _{i=1}^{r}a_{2i-1}\cdot a_{2i}$
and
![]() $Q = \sum _{i=1}^{r}b_{2i-1}\cdot b_{2i}$
be two different minimal representations of Q. Then
$Q = \sum _{i=1}^{r}b_{2i-1}\cdot b_{2i}$
be two different minimal representations of Q. Then
![]() $\operatorname {span}\{{{a}_1,\ldots , {a}_{2r}}\} =\operatorname {span}\{{{b}_1,\ldots , {b}_{2r}}\}$
.
$\operatorname {span}\{{{a}_1,\ldots , {a}_{2r}}\} =\operatorname {span}\{{{b}_1,\ldots , {b}_{2r}}\}$
.
Proof. Note that, if the statement does not hold, then, without loss of generality,
![]() $a_1$
is not contained in the span of the
$a_1$
is not contained in the span of the
![]() $b_i$
’s. This means that when setting
$b_i$
’s. This means that when setting
![]() $a_1=0$
the
$a_1=0$
the
![]() $b_i$
’s are not affected on the one hand, thus Q remains the same function of the
$b_i$
’s are not affected on the one hand, thus Q remains the same function of the
![]() $b_i$
’s, and in particular
$b_i$
’s, and in particular
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{a_1=0})=r$
, but on the other hand,
$\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{a_1=0})=r$
, but on the other hand,
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{a_1=0})=r-1$
(when considering its representation with the
$\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{a_1=0})=r-1$
(when considering its representation with the
![]() $a_i$
’s), in contradiction.
$a_i$
’s), in contradiction.
This claim allows us to define the notion of minimal space of a quadratic polynomial Q, which we shall denote
![]() $\text {Lin}(Q)$
.
$\text {Lin}(Q)$
.
Definition 2.14. Let Q be a quadratic polynomial such that
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q) = r$
, and let
$\operatorname {\mathrm {rank}}_{\text {s}}(Q) = r$
, and let
![]() $Q = \sum \limits _{i=1}^r a_{2i-1}\cdot a_{2i}$
be some minimal representation of Q. Define
$Q = \sum \limits _{i=1}^r a_{2i-1}\cdot a_{2i}$
be some minimal representation of Q. Define
![]() $\text {Lin}(Q):= \operatorname {span}\{{{a}_1,\ldots , {a}_{2r}}\}$
, and also denote
$\text {Lin}(Q):= \operatorname {span}\{{{a}_1,\ldots , {a}_{2r}}\}$
, and also denote
![]() $\text {Lin}({Q}_1,\ldots , {Q}_{k}) = \sum \limits _{i=1}^k \text {Lin}(Q_i)$
.
$\text {Lin}({Q}_1,\ldots , {Q}_{k}) = \sum \limits _{i=1}^k \text {Lin}(Q_i)$
.
Theorem 2.13 shows that the minimal space is well defined. The following fact is easy to verify.
Fact 2.15. Let
![]() $Q=\sum _{i=1}^{m}a_{2i-1}\cdot a_{2i}$
be a homogeneous quadratic polynomial, then
$Q=\sum _{i=1}^{m}a_{2i-1}\cdot a_{2i}$
be a homogeneous quadratic polynomial, then
![]() $\text {Lin}(Q)\subseteq \operatorname {span}\{{{a}_1,\ldots , {a}_{2m}}\}$
.
$\text {Lin}(Q)\subseteq \operatorname {span}\{{{a}_1,\ldots , {a}_{2m}}\}$
.
We now give some basic claims regarding
![]() $\operatorname {\mathrm {rank}}_{\text {s}}$
.
$\operatorname {\mathrm {rank}}_{\text {s}}$
.
Claim 2.16. Let Q be a homogeneous quadratic polynomial with
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q)=r$
, and let
$\operatorname {\mathrm {rank}}_{\text {s}}(Q)=r$
, and let
![]() $V \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be a linear space of linear forms such that
$V \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be a linear space of linear forms such that
![]() $\dim (V)=\Delta $
. Then
$\dim (V)=\Delta $
. Then
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0})\geq r-\Delta $
.
$\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0})\geq r-\Delta $
.
Proof. Assume without loss of generality
![]() $V = \operatorname {span}\{{{x}_1,\ldots , {x}_{\Delta }}\}$
, and consider
$V = \operatorname {span}\{{{x}_1,\ldots , {x}_{\Delta }}\}$
, and consider
![]() $Q\in \mathbb {C}[x_{\Delta +1},\ldots ,x_n][{x}_1,\ldots , {x}_{\Delta }]$
. There are
$Q\in \mathbb {C}[x_{\Delta +1},\ldots ,x_n][{x}_1,\ldots , {x}_{\Delta }]$
. There are
![]() ${a}_1,\ldots , {a}_{\Delta } \in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
and
${a}_1,\ldots , {a}_{\Delta } \in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
and
![]() $Q' \in \mathbb {C}[x_{\Delta +1},\ldots ,x_n]$
such that
$Q' \in \mathbb {C}[x_{\Delta +1},\ldots ,x_n]$
such that
![]() $Q = \sum _{i=1}^{\Delta } a_ix_i + Q'$
, where
$Q = \sum _{i=1}^{\Delta } a_ix_i + Q'$
, where
![]() $Q|_{V=0} = Q'$
. As
$Q|_{V=0} = Q'$
. As
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(\sum _{i=1}^{\Delta } a_ix_i ) \leq \Delta $
, it must be that
$\operatorname {\mathrm {rank}}_{\text {s}}(\sum _{i=1}^{\Delta } a_ix_i ) \leq \Delta $
, it must be that
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0}) \geq r-\Delta $
.
$\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0}) \geq r-\Delta $
.
Claim 2.17. Let
![]() $P_1\in \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$
, and
$P_1\in \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$
, and
![]() $P_2 = y_1y_2\in \mathbb {C}[y_1,y_2]$
. Then
$P_2 = y_1y_2\in \mathbb {C}[y_1,y_2]$
. Then
![]() $ \operatorname {\mathrm {rank}}_{\text {s}} (P_1+P_2) = \operatorname {\mathrm {rank}}_{\text {s}}(P_1) + 1$
. Moreover,
$ \operatorname {\mathrm {rank}}_{\text {s}} (P_1+P_2) = \operatorname {\mathrm {rank}}_{\text {s}}(P_1) + 1$
. Moreover,
![]() $y_1,y_2 \in \text {Lin}(P_1+P_2).$
$y_1,y_2 \in \text {Lin}(P_1+P_2).$
Proof. Denote
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(P_1) = r$
, and assume towards a contradiction that there are
$\operatorname {\mathrm {rank}}_{\text {s}}(P_1) = r$
, and assume towards a contradiction that there are
![]() ${a}_1,\ldots , {a}_{2r}$
linear forms in
${a}_1,\ldots , {a}_{2r}$
linear forms in
![]() $\mathbb {C}[x_1,\dots ,x_k,y_1,y_2]$
such that
$\mathbb {C}[x_1,\dots ,x_k,y_1,y_2]$
such that
![]() $P_1+P_2 = \sum \limits _{i=1}^{r}a_{2i-1}a_{2i}$
. Clearly,
$P_1+P_2 = \sum \limits _{i=1}^{r}a_{2i-1}a_{2i}$
. Clearly,
![]() $\sum \limits _{i=1}^{r}a_{2i-1}a_{2i} \equiv _{y_1} P_1$
. As
$\sum \limits _{i=1}^{r}a_{2i-1}a_{2i} \equiv _{y_1} P_1$
. As
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(P_1) = r$
, this is a minimal representation of
$\operatorname {\mathrm {rank}}_{\text {s}}(P_1) = r$
, this is a minimal representation of
![]() $P_1$
. Hence, for every i,
$P_1$
. Hence, for every i,
![]() $a_i|_{y_1=0} \in \text {Lin}(P_1)\subset \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$
. Moreover, from the minimality of r,
$a_i|_{y_1=0} \in \text {Lin}(P_1)\subset \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$
. Moreover, from the minimality of r,
![]() $a_i|_{y_1=0} \neq 0$
. Therefore, as
$a_i|_{y_1=0} \neq 0$
. Therefore, as
![]() $y_1$
and
$y_1$
and
![]() $y_2$
are linearly independent, we deduce that all the coefficients of
$y_2$
are linearly independent, we deduce that all the coefficients of
![]() $y_2$
in all the
$y_2$
in all the
![]() $a_i$
’s are 0. By reversing the roles of
$a_i$
’s are 0. By reversing the roles of
![]() $y_1$
and
$y_1$
and
![]() $y_2$
, we can conclude that
$y_2$
, we can conclude that
![]() ${a}_1,\ldots , {a}_{2r}\subset \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$
which means that
${a}_1,\ldots , {a}_{2r}\subset \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$
which means that
![]() $P_1+P_2$
does not depend on
$P_1+P_2$
does not depend on
![]() $y_1$
nor on
$y_1$
nor on
![]() $y_2$
, in contradiction. Consider a minimal representation
$y_2$
, in contradiction. Consider a minimal representation
![]() $P_1 = \sum _{i=1}^{2r} b_{2i-1}b_{2i}$
, from the fact that
$P_1 = \sum _{i=1}^{2r} b_{2i-1}b_{2i}$
, from the fact that
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(P_1+P_2) = r+1$
it follows that
$\operatorname {\mathrm {rank}}_{\text {s}}(P_1+P_2) = r+1$
it follows that
![]() $P_1+P_2 = \sum _{i=1}^{2r} b_{2i-1}b_{2i}+y_1y_2$
is a minimal representation of
$P_1+P_2 = \sum _{i=1}^{2r} b_{2i-1}b_{2i}+y_1y_2$
is a minimal representation of
![]() $P_1+P_2$
and thus
$P_1+P_2$
and thus
![]() $\text {Lin}(P_1+P_2) =\text {Lin}(P_1) + \operatorname {span}\{{y_1,y_2}\}$
.
$\text {Lin}(P_1+P_2) =\text {Lin}(P_1) + \operatorname {span}\{{y_1,y_2}\}$
.
Corollary 2.18. Let a and b be linearly independent linear forms. Then, if
![]() $c,d,e$
and f are linear forms such that
$c,d,e$
and f are linear forms such that
![]() $ab+cd=ef$
, then
$ab+cd=ef$
, then
![]() $\dim (\operatorname {span}\{{a,b}\}\cap \operatorname {span}\{{c,d}\})\geq 1$
.
$\dim (\operatorname {span}\{{a,b}\}\cap \operatorname {span}\{{c,d}\})\geq 1$
.
Corollary 2.19. Let
![]() $a,b,c$
and d be linear forms such that a and b are linearly independent, and V be a linear space of linear forms. Assume
$a,b,c$
and d be linear forms such that a and b are linearly independent, and V be a linear space of linear forms. Assume
![]() $\{0\} \neq \text {Lin}(ab-cd) \subseteq V$
then
$\{0\} \neq \text {Lin}(ab-cd) \subseteq V$
then
![]() $\operatorname {span}\{{a,b}\} \cap V\neq \{0\}$
.
$\operatorname {span}\{{a,b}\} \cap V\neq \{0\}$
.
Proof. Let
![]() $ Q\in \mathbb {C}[V]$
be such that
$ Q\in \mathbb {C}[V]$
be such that
![]() $ab-cd=Q$
. As
$ab-cd=Q$
. As
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q-ab)=\operatorname {\mathrm {rank}}_{\text {s}}(-cd)=1$
, Theorem 2.17 implies that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q-ab)=\operatorname {\mathrm {rank}}_{\text {s}}(-cd)=1$
, Theorem 2.17 implies that
![]() $\operatorname {span}\{{a,b}\} \cap V\neq \{0\}$
.
$\operatorname {span}\{{a,b}\} \cap V\neq \{0\}$
.
Lemma 2.20. Let
![]() $P_V\in \mathbb {C}[V]$
be a polynomial defined over a linear space of linear forms V, and let
$P_V\in \mathbb {C}[V]$
be a polynomial defined over a linear space of linear forms V, and let
![]() $c_1,c_2$
satisfy
$c_1,c_2$
satisfy
![]() $ c_1 \notin V$
and
$ c_1 \notin V$
and
![]() $c_2 \notin \operatorname {span}\{{c_1 ,V}\}$
. If there are linear forms
$c_2 \notin \operatorname {span}\{{c_1 ,V}\}$
. If there are linear forms
![]() $e,f$
such that
$e,f$
such that
then, without loss of generality,
![]() $e \in \operatorname {span}\{{c_1,c_2,V}\}$
and
$e \in \operatorname {span}\{{c_1,c_2,V}\}$
and
![]() $e \notin \operatorname {span}\{{c_1,V}\}\cup \operatorname {span}\{{c_2,V}\}$
.
$e \notin \operatorname {span}\{{c_1,V}\}\cup \operatorname {span}\{{c_2,V}\}$
.
Proof. First, note that
![]() $e\not \in V$
as otherwise we would have that
$e\not \in V$
as otherwise we would have that
![]() $c_1\equiv _V c_2$
, in contradiction.
$c_1\equiv _V c_2$
, in contradiction.
By our assumption,
![]() $ef =P_V$
modulo
$ef =P_V$
modulo
![]() $c_1,c_2$
. We can therefore assume without loss of generality that
$c_1,c_2$
. We can therefore assume without loss of generality that
![]() $e \in \operatorname {span}\{{c_1,c_2,V}\}$
. Assume towards a contradiction and without loss of generality that
$e \in \operatorname {span}\{{c_1,c_2,V}\}$
. Assume towards a contradiction and without loss of generality that
![]() $e = \lambda c_1 + v_e$
, where
$e = \lambda c_1 + v_e$
, where
![]() $\lambda \neq 0$
and
$\lambda \neq 0$
and
![]() $v_e\in V$
. Consider the equation
$v_e\in V$
. Consider the equation
![]() $c_1(\varepsilon _1 c_1 + v_1) + c_2(\varepsilon _2 c_2 + v_2) + ef = P_V$
modulo
$c_1(\varepsilon _1 c_1 + v_1) + c_2(\varepsilon _2 c_2 + v_2) + ef = P_V$
modulo
![]() $c_1$
. We have that
$c_1$
. We have that
![]() $c_2(\varepsilon _2 c_2 + v_2) + v_e f \equiv _{c_1} P_V$
which implies that
$c_2(\varepsilon _2 c_2 + v_2) + v_e f \equiv _{c_1} P_V$
which implies that
![]() $\varepsilon _2=0$
. Consequently, we also have that
$\varepsilon _2=0$
. Consequently, we also have that
![]() $f = \mu c_2 + \eta c_1 + v_f$
, for some
$f = \mu c_2 + \eta c_1 + v_f$
, for some
![]() $\mu \neq 0$
and
$\mu \neq 0$
and
![]() $v_f \in V$
. We now observe that the product
$v_f \in V$
. We now observe that the product
![]() $c_1c_2$
has a nonzero coefficient
$c_1c_2$
has a nonzero coefficient
![]() $\lambda \mu $
in
$\lambda \mu $
in
![]() $ef$
and a zero coefficient in
$ef$
and a zero coefficient in
![]() $P_V - c_2(\varepsilon _2 c_2 + v_2) + c_1(\varepsilon _1 c_1 + v_1) $
, in contradiction.
$P_V - c_2(\varepsilon _2 c_2 + v_2) + c_1(\varepsilon _1 c_1 + v_1) $
, in contradiction.
2.4 Linear algebra facts
Claim 2.21. Let
![]() $V = \sum _{i=1}^m V_i$
where
$V = \sum _{i=1}^m V_i$
where
![]() $V_i$
are linear subspaces, and for every i,
$V_i$
are linear subspaces, and for every i,
![]() $\dim (V_i) = 2$
. If for every
$\dim (V_i) = 2$
. If for every
![]() $i\neq j \in [m]$
,
$i\neq j \in [m]$
,
![]() $\dim (V_i\cap V_j) = 1$
, then either
$\dim (V_i\cap V_j) = 1$
, then either
![]() $\dim (\bigcap _{i=1}^m V_i) = 1$
or
$\dim (\bigcap _{i=1}^m V_i) = 1$
or
![]() $\dim (V)=3$
.
$\dim (V)=3$
.
Proof. Let
![]() $w \in V_1\cap V_2$
. Complete it to basis of
$w \in V_1\cap V_2$
. Complete it to basis of
![]() $V_1$
and
$V_1$
and
![]() $V_2$
:
$V_2$
:
![]() $V_1 = \operatorname {span}\{{u_1,w}\}$
and
$V_1 = \operatorname {span}\{{u_1,w}\}$
and
![]() $V_2 = \operatorname {span}\{{u_2,w}\}$
. Assume that
$V_2 = \operatorname {span}\{{u_2,w}\}$
. Assume that
![]() $\dim (\bigcap _{i=1}^m V_i) = 0$
. Then, there is some i for which
$\dim (\bigcap _{i=1}^m V_i) = 0$
. Then, there is some i for which
![]() $w \notin V_i$
. Let
$w \notin V_i$
. Let
![]() $x_1 \in V_i\cap V_1$
, and so
$x_1 \in V_i\cap V_1$
, and so
![]() $x_1 = \alpha _1 u_1 + \beta _1 w$
, where
$x_1 = \alpha _1 u_1 + \beta _1 w$
, where
![]() $\alpha _1 \neq 0$
. Similarly, let
$\alpha _1 \neq 0$
. Similarly, let
![]() $x_2 \in V_i\cap V_2$
. Since
$x_2 \in V_i\cap V_2$
. Since
![]() $w \notin V_i$
,
$w \notin V_i$
,
![]() $x_2 = \alpha _2 u_2 + \beta _2 w$
, where
$x_2 = \alpha _2 u_2 + \beta _2 w$
, where
![]() $\alpha _2 \neq 0$
. Note that
$\alpha _2 \neq 0$
. Note that
![]() $x_1 \notin \operatorname {span}\{{ x_2}\}$
, as
$x_1 \notin \operatorname {span}\{{ x_2}\}$
, as
![]() $\dim (V_1\cap V_2) = 1$
, and w is already in their intersection. Thus, we have
$\dim (V_1\cap V_2) = 1$
, and w is already in their intersection. Thus, we have
![]() $V_i = \operatorname {span}\{{x_1,x_2}\} \subset \operatorname {span}\{{w, u_1, u_2}\}$
.
$V_i = \operatorname {span}\{{x_1,x_2}\} \subset \operatorname {span}\{{w, u_1, u_2}\}$
.
Now, consider any other
![]() $j \in [m]$
. If
$j \in [m]$
. If
![]() $V_j$
does not contain w, we can apply the same argument as we did for
$V_j$
does not contain w, we can apply the same argument as we did for
![]() $V_i$
and conclude that
$V_i$
and conclude that
![]() $V_j \subset \operatorname {span}\{{w,u_1,u_2}\}$
. On the other hand, if
$V_j \subset \operatorname {span}\{{w,u_1,u_2}\}$
. On the other hand, if
![]() $w \in V_j$
, then let
$w \in V_j$
, then let
![]() $x_j \in V_i\cap V_j$
. It is easy to see that
$x_j \in V_i\cap V_j$
. It is easy to see that
![]() $x_j, w$
are linearly independent and so
$x_j, w$
are linearly independent and so
![]() $V_j = \operatorname {span}\{{w,x_j}\} \subset \operatorname {span}\{{w,V_i}\} \subseteq \operatorname {span}\{{w, u_1,u_2}\}$
. Thus, in any case
$V_j = \operatorname {span}\{{w,x_j}\} \subset \operatorname {span}\{{w,V_i}\} \subseteq \operatorname {span}\{{w, u_1,u_2}\}$
. Thus, in any case
![]() $V_j \subset \operatorname {span}\{{w, u_1,u_2}\}$
. In particular,
$V_j \subset \operatorname {span}\{{w, u_1,u_2}\}$
. In particular,
![]() $\sum _j V_j \subseteq \operatorname {span}\{{w, u_1,u_2}\}$
as claimed.
$\sum _j V_j \subseteq \operatorname {span}\{{w, u_1,u_2}\}$
as claimed.
Lemma 2.22. Let V be a linear space of dimension
![]() $\leq 4$
, and let
$\leq 4$
, and let
![]() $V_1,V_2,V_3 \subset V$
each of dimension
$V_1,V_2,V_3 \subset V$
each of dimension
![]() $\geq 2$
such that
$\geq 2$
such that
![]() $V_1\not \subseteq V_2$
and
$V_1\not \subseteq V_2$
and
![]() $V_3\not \subseteq V_2 + V_1$
then
$V_3\not \subseteq V_2 + V_1$
then
![]() $V = V_1+V_2+V_3$
.
$V = V_1+V_2+V_3$
.
Proof. As
![]() $V_1\not \subseteq V_2$
, we have that
$V_1\not \subseteq V_2$
, we have that
![]() $\dim (V_1+V_2)\geq 3$
. Similarly, we get
$\dim (V_1+V_2)\geq 3$
. Similarly, we get
![]() $4\leq \dim (V_1+V_2+V_3)\leq \dim (V)=4$
.
$4\leq \dim (V_1+V_2+V_3)\leq \dim (V)=4$
.
The following corollary is an easy consequence of Theorem 2.22.
Corollary 2.23. Let Q be an irreducible quadratic polynomial. Let
![]() $\{P_i\}_{i=1}^{k}$
be irreducible quadratic polynomials such that
$\{P_i\}_{i=1}^{k}$
be irreducible quadratic polynomials such that
![]() $\dim (\text {Lin}(Q)) \leq 4$
, and for every
$\dim (\text {Lin}(Q)) \leq 4$
, and for every
![]() $i\in [k]$
,
$i\in [k]$
,
![]() $\dim (\text {Lin}(Q)\cap \text {Lin}(P_i)) \geq 2$
. Assume further that
$\dim (\text {Lin}(Q)\cap \text {Lin}(P_i)) \geq 2$
. Assume further that
![]() $\text {Lin}(P_1)\not \subset \text {Lin}(Q)$
,
$\text {Lin}(P_1)\not \subset \text {Lin}(Q)$
,
![]() $\text {Lin}(P_2)\not \subset \text {Lin}(Q)+\text {Lin}(P_1) , \ldots , \text {Lin}(P_k)\not \subset \text {Lin}(Q)+\text {Lin}(P_1)+\ldots +\text {Lin}(P_{k-1})$
. Then,
$\text {Lin}(P_2)\not \subset \text {Lin}(Q)+\text {Lin}(P_1) , \ldots , \text {Lin}(P_k)\not \subset \text {Lin}(Q)+\text {Lin}(P_1)+\ldots +\text {Lin}(P_{k-1})$
. Then,
![]() $k\leq 3$
.
$k\leq 3$
.
2.5 Projection mappings
In this section, we present and apply a new technique which allows us to simplify the structure of quadratic polynomials. Naively, when we want to simplify a polynomial equation, we can project it on a subset of the variables. Unfortunately, this projection does not necessarily preserve pairwise linear independence, which is a crucial property in our proofs. To remedy this fact, we present a set of mappings, which are somewhat similar to projections but do preserve pairwise linear independence among polynomials that are not in
![]() $\mathbb {C}[V]$
, where V is the space being projected.
$\mathbb {C}[V]$
, where V is the space being projected.
Definition 2.24. Let
![]() $V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$
be a
$V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$
be a
![]() $\Delta $
-dimensional linear space of linear forms, and let
$\Delta $
-dimensional linear space of linear forms, and let
![]() $\{{u}_1,\ldots , {u}_{{n-\Delta }}\}$
be a basis for
$\{{u}_1,\ldots , {u}_{{n-\Delta }}\}$
be a basis for
![]() $V^{\perp }$
. For
$V^{\perp }$
. For
![]() ${\boldsymbol {\alpha }} = ({\alpha }_1,\ldots , {\alpha }_{\Delta })\in \mathbb {C}^{\Delta }$
, we define
${\boldsymbol {\alpha }} = ({\alpha }_1,\ldots , {\alpha }_{\Delta })\in \mathbb {C}^{\Delta }$
, we define
![]() $T_{{\boldsymbol {\alpha }}, V} : \mathbb {C}[ {x}_1,\ldots , {x}_{n}] \mapsto \mathbb {C}[{x}_1,\ldots , {x}_{n},z]$
, where z is a new variable, to be the linear map given by the following action on the basis vectors:
$T_{{\boldsymbol {\alpha }}, V} : \mathbb {C}[ {x}_1,\ldots , {x}_{n}] \mapsto \mathbb {C}[{x}_1,\ldots , {x}_{n},z]$
, where z is a new variable, to be the linear map given by the following action on the basis vectors:
![]() $T_{{\boldsymbol {\alpha }}, V}(v_i) = \alpha _i z$
and
$T_{{\boldsymbol {\alpha }}, V}(v_i) = \alpha _i z$
and
![]() $T_{{\boldsymbol {\alpha }}, V}(u_i)=u_i$
.
$T_{{\boldsymbol {\alpha }}, V}(u_i)=u_i$
.
Observation 2.25.
![]() $T_{{\boldsymbol {\alpha }}, V}$
is a linear transformation and is also a ring homomorphism. This follows from the fact that a basis for
$T_{{\boldsymbol {\alpha }}, V}$
is a linear transformation and is also a ring homomorphism. This follows from the fact that a basis for
![]() $\operatorname {span}\{{{x}_1,\ldots , {x}_{n}}\}$
is a basis for
$\operatorname {span}\{{{x}_1,\ldots , {x}_{n}}\}$
is a basis for
![]() $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
as a
$\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
as a
![]() $\mathbb {C}$
-algebra.
$\mathbb {C}$
-algebra.
In the remaining claims in this section, we shall always assume that
![]() $V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$
is a a
$V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$
is a a
![]() $\Delta $
-dimensional linear space of linear forms. We define
$\Delta $
-dimensional linear space of linear forms. We define
![]() $T_{{\boldsymbol {\alpha }}, V}$
with respect to this basis.
$T_{{\boldsymbol {\alpha }}, V}$
with respect to this basis.
Claim 2.26. Let
![]() $V\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$
be a
$V\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$
be a
![]() $\Delta $
-dimensional linear space of linear forms. Let F and G be two polynomials that share no common irreducible factor. Then, with probability
$\Delta $
-dimensional linear space of linear forms. Let F and G be two polynomials that share no common irreducible factor. Then, with probability
![]() $1$
over the choice of
$1$
over the choice of
![]() ${\boldsymbol {\alpha }} \in [0,1]^{\Delta }$
(say, according to the uniform distribution),
${\boldsymbol {\alpha }} \in [0,1]^{\Delta }$
(say, according to the uniform distribution),
![]() $T_{{\boldsymbol {\alpha }}, V}(F)$
and
$T_{{\boldsymbol {\alpha }}, V}(F)$
and
![]() $T_{{\boldsymbol {\alpha }}, V}(G)$
do not share a common factor that is not a polynomial in z.
$T_{{\boldsymbol {\alpha }}, V}(G)$
do not share a common factor that is not a polynomial in z.
Proof. Let
![]() $\lbrace {u}_1,\ldots , {u}_{{n-\Delta }}\rbrace $
be a basis for
$\lbrace {u}_1,\ldots , {u}_{{n-\Delta }}\rbrace $
be a basis for
![]() $V^{\perp }$
. We think of F and G as polynomials in
$V^{\perp }$
. We think of F and G as polynomials in
![]() $\mathbb {C}[{v}_1,\ldots , {v}_{\Delta }, {u}_1,\ldots , {u}_{n-\Delta }]$
. As
$\mathbb {C}[{v}_1,\ldots , {v}_{\Delta }, {u}_1,\ldots , {u}_{n-\Delta }]$
. As
![]() $T_{{\boldsymbol {\alpha }},V}: \mathbb {C}[{v}_1,\ldots , {v}_{\Delta }, {u}_1,\ldots , {u}_{n-\Delta }] \rightarrow \mathbb {C}[z, {u}_1,\ldots , {u}_{n-\Delta }]$
, Theorem 2.11 implies that, if
$T_{{\boldsymbol {\alpha }},V}: \mathbb {C}[{v}_1,\ldots , {v}_{\Delta }, {u}_1,\ldots , {u}_{n-\Delta }] \rightarrow \mathbb {C}[z, {u}_1,\ldots , {u}_{n-\Delta }]$
, Theorem 2.11 implies that, if
![]() $T_{{\boldsymbol {\alpha }}, V}(F)$
and
$T_{{\boldsymbol {\alpha }}, V}(F)$
and
![]() $T_{{\boldsymbol {\alpha }}, V}(G)$
share a common factor that is not a polynomial in z, then, without loss of generality, their resultant with respect to
$T_{{\boldsymbol {\alpha }}, V}(G)$
share a common factor that is not a polynomial in z, then, without loss of generality, their resultant with respect to
![]() $u_1$
is zero. Theorem 2.11 also implies that the resultant of F and G with respect to
$u_1$
is zero. Theorem 2.11 also implies that the resultant of F and G with respect to
![]() $u_1$
is not zero. Observe that, with probability
$u_1$
is not zero. Observe that, with probability
![]() $1$
over the choice of
$1$
over the choice of
![]() ${\boldsymbol {\alpha }}$
, we have that
${\boldsymbol {\alpha }}$
, we have that
![]() $\deg _{u_1}(F) = \deg _{u_1}(T_{{\boldsymbol {\alpha }}, V}(F))$
and
$\deg _{u_1}(F) = \deg _{u_1}(T_{{\boldsymbol {\alpha }}, V}(F))$
and
![]() $\deg _{u_1}(G) = \deg _{u_1}(T_{{\boldsymbol {\alpha }}, V}(G))$
. As
$\deg _{u_1}(G) = \deg _{u_1}(T_{{\boldsymbol {\alpha }}, V}(G))$
. As
![]() $T_{{\boldsymbol {\alpha }}, V}$
is a ring homomorphism, this implies that
$T_{{\boldsymbol {\alpha }}, V}$
is a ring homomorphism, this implies that
![]() $\mathrm {Res}_{u_1}(T_{{\boldsymbol {\alpha }}, V}(G), T_{{\boldsymbol {\alpha }}, V}(F)) = T_{{\boldsymbol {\alpha }}, V}(\mathrm {Res}_{u_1}(G, F))$
. The Schwartz–Zippel–DeMillo–Lipton lemma now implies that sending each basis element of V to a random multiple of z, chosen uniformly from
$\mathrm {Res}_{u_1}(T_{{\boldsymbol {\alpha }}, V}(G), T_{{\boldsymbol {\alpha }}, V}(F)) = T_{{\boldsymbol {\alpha }}, V}(\mathrm {Res}_{u_1}(G, F))$
. The Schwartz–Zippel–DeMillo–Lipton lemma now implies that sending each basis element of V to a random multiple of z, chosen uniformly from
![]() $(0,1)$
, will keep the resultant nonzero with probability
$(0,1)$
, will keep the resultant nonzero with probability
![]() $1$
. This also means that
$1$
. This also means that
![]() $T_{{\boldsymbol {\alpha }}, V}(F)$
and
$T_{{\boldsymbol {\alpha }}, V}(F)$
and
![]() $T_{{\boldsymbol {\alpha }}, V}(G)$
share no common factor.
$T_{{\boldsymbol {\alpha }}, V}(G)$
share no common factor.
Corollary 2.27. Let V be a
![]() $\Delta $
-dimensional linear space of linear forms. Let F and G be two linearly independent, irreducible quadratics such that
$\Delta $
-dimensional linear space of linear forms. Let F and G be two linearly independent, irreducible quadratics such that
![]() $\text {Lin}(F),\text {Lin}(G)\not \subseteq V$
. Then, with probability
$\text {Lin}(F),\text {Lin}(G)\not \subseteq V$
. Then, with probability
![]() $1$
over the choice of
$1$
over the choice of
![]() ${\boldsymbol {\alpha }} \in [0,1]^{\Delta }$
(say, according to the uniform distribution),
${\boldsymbol {\alpha }} \in [0,1]^{\Delta }$
(say, according to the uniform distribution),
![]() $T_{{\boldsymbol {\alpha }}, V}(F)$
and
$T_{{\boldsymbol {\alpha }}, V}(F)$
and
![]() $T_{{\boldsymbol {\alpha }}, V}(G)$
are linearly independent.
$T_{{\boldsymbol {\alpha }}, V}(G)$
are linearly independent.
Proof. As F and G are irreducible they share no common factors. Theorem 2.26 implies that
![]() $T_{{\boldsymbol {\alpha }}, V}(F)$
and
$T_{{\boldsymbol {\alpha }}, V}(F)$
and
![]() $T_{{\boldsymbol {\alpha }}, V}(G)$
do not share a common factor that is not a polynomial in z. The Schwartz–Zippel–DeMillo–Lipton lemma implies that, with probability
$T_{{\boldsymbol {\alpha }}, V}(G)$
do not share a common factor that is not a polynomial in z. The Schwartz–Zippel–DeMillo–Lipton lemma implies that, with probability
![]() $1$
,
$1$
,
![]() $T_{{\boldsymbol {\alpha }}, V}(F)$
and
$T_{{\boldsymbol {\alpha }}, V}(F)$
and
![]() $T_{{\boldsymbol {\alpha }}, V}(G)$
are not polynomials in z, and therefore, they are linearly independent.
$T_{{\boldsymbol {\alpha }}, V}(G)$
are not polynomials in z, and therefore, they are linearly independent.
Claim 2.28. Let Q be an irreducible quadratic polynomial and V a
![]() $\Delta $
-dimensional linear space. Then for every
$\Delta $
-dimensional linear space. Then for every
![]() ${\boldsymbol {\alpha }} \in \mathbb {C}^{\Delta }$
,
${\boldsymbol {\alpha }} \in \mathbb {C}^{\Delta }$
,
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)) \geq \operatorname {\mathrm {rank}}_{\text {s}}(Q)-\Delta $
.
$\operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)) \geq \operatorname {\mathrm {rank}}_{\text {s}}(Q)-\Delta $
.
Proof.
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)) \geq \operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)|_{z=0}) = \operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0}) \geq \operatorname {\mathrm {rank}}_{\text {s}}(Q)-\Delta $
, where the last inequality follows from Theorem 2.16.
$\operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)) \geq \operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)|_{z=0}) = \operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0}) \geq \operatorname {\mathrm {rank}}_{\text {s}}(Q)-\Delta $
, where the last inequality follows from Theorem 2.16.
Claim 2.29. Let
![]() ${\mathcal {Q}}$
be a set of quadratics and V be a
${\mathcal {Q}}$
be a set of quadratics and V be a
![]() $\Delta $
-dimensional linear space. Then, if there are linearly independent vectors,
$\Delta $
-dimensional linear space. Then, if there are linearly independent vectors,
![]() $\{{\boldsymbol {\alpha }}^1,\dots , {\boldsymbol {\alpha }}^{\Delta } \}\subset \mathbb {C}^{\Delta }$
such that, for every i,Footnote
3
$\{{\boldsymbol {\alpha }}^1,\dots , {\boldsymbol {\alpha }}^{\Delta } \}\subset \mathbb {C}^{\Delta }$
such that, for every i,Footnote
3
![]() $\dim (\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})))\leq \sigma $
, then
$\dim (\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})))\leq \sigma $
, then
![]() $\dim (\text {Lin}({\mathcal {Q}}))\leq (\sigma +1) \Delta $
.
$\dim (\text {Lin}({\mathcal {Q}}))\leq (\sigma +1) \Delta $
.
Proof. As
![]() $\dim (\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})))\leq \sigma $
, there are
$\dim (\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})))\leq \sigma $
, there are
![]() ${u^i}_1,\ldots , {u^i}_{\sigma } \subset V^{\perp }$
such that
${u^i}_1,\ldots , {u^i}_{\sigma } \subset V^{\perp }$
such that
![]() $\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})) \subseteq \operatorname {span}\{{z,{u^i}_1,\ldots , {u^i}_{\sigma } }\}$
. We will show that
$\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})) \subseteq \operatorname {span}\{{z,{u^i}_1,\ldots , {u^i}_{\sigma } }\}$
. We will show that
![]() $\text {Lin}({\mathcal {Q}}) \subset V + \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$
, which is of dimension at most
$\text {Lin}({\mathcal {Q}}) \subset V + \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$
, which is of dimension at most
![]() $\Delta + \sigma \Delta $
.
$\Delta + \sigma \Delta $
.
Let
![]() $P \in {\mathcal {Q}}$
, then there are linear forms,
$P \in {\mathcal {Q}}$
, then there are linear forms,
![]() ${a}_1,\ldots , {a}_{\Delta } \subset V^{\perp }$
and polynomials
${a}_1,\ldots , {a}_{\Delta } \subset V^{\perp }$
and polynomials
![]() $P_{V} \in \mathbb {C}[V]$
and
$P_{V} \in \mathbb {C}[V]$
and
![]() $P'\in \mathbb {C}[V^{\perp }]$
such that
$P'\in \mathbb {C}[V^{\perp }]$
such that
 $$ \begin{align*} P = P_{V} + \sum\limits_{j=1}^{\Delta} a_jv_j + P'. \end{align*} $$
$$ \begin{align*} P = P_{V} + \sum\limits_{j=1}^{\Delta} a_jv_j + P'. \end{align*} $$
Therefore, after taking the projection for a specific
![]() $T_{{\boldsymbol {\alpha }}^i, V}$
, for some
$T_{{\boldsymbol {\alpha }}^i, V}$
, for some
![]() $\gamma \in \mathbb {C}$
,
$\gamma \in \mathbb {C}$
,
 $$ \begin{align*} T_{{\boldsymbol{\alpha}}^i,V}(P) = \gamma z^2 + \left(\sum\limits_{j=1}^{\Delta} \alpha^i_ja_j\right) z + P'. \end{align*} $$
$$ \begin{align*} T_{{\boldsymbol{\alpha}}^i,V}(P) = \gamma z^2 + \left(\sum\limits_{j=1}^{\Delta} \alpha^i_ja_j\right) z + P'. \end{align*} $$
Denote
 $b_{P,i} = \sum \limits _{j=1}^{\Delta } \alpha ^i_ja_j$
. By Theorem 2.27, if
$b_{P,i} = \sum \limits _{j=1}^{\Delta } \alpha ^i_ja_j$
. By Theorem 2.27, if
![]() ${a}_1,\ldots , {a}_{\Delta }$
are not all zeros, then, with probability
${a}_1,\ldots , {a}_{\Delta }$
are not all zeros, then, with probability
![]() $1$
,
$1$
,
![]() $b_{P,i} \neq {\mathbf {0}}$
.
$b_{P,i} \neq {\mathbf {0}}$
.
If
![]() $b_{P,i}\notin \text {Lin}(P')$
, then from Theorem 2.17 it follows that
$b_{P,i}\notin \text {Lin}(P')$
, then from Theorem 2.17 it follows that
![]() $\lbrace z, b_{P,i}, \text {Lin}(P')\rbrace \subseteq \operatorname {span}\{{ \text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}(P))}\}$
. If, on the other hand,
$\lbrace z, b_{P,i}, \text {Lin}(P')\rbrace \subseteq \operatorname {span}\{{ \text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}(P))}\}$
. If, on the other hand,
![]() $b_{P,i} \in \text {Lin}(P')$
, then clearly
$b_{P,i} \in \text {Lin}(P')$
, then clearly
![]() $\lbrace b_{P,i}, \text {Lin}(P')\rbrace \subseteq \operatorname {span}\{{ z, \text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}(P))}\}$
. To conclude, in either case,
$\lbrace b_{P,i}, \text {Lin}(P')\rbrace \subseteq \operatorname {span}\{{ z, \text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}(P))}\}$
. To conclude, in either case,
![]() $\{b_{P,i},\text {Lin}(P')\} \subseteq \operatorname {span}\{{z, {u^i}_1,\ldots , {u^i}_{\sigma }}\}.$
$\{b_{P,i},\text {Lin}(P')\} \subseteq \operatorname {span}\{{z, {u^i}_1,\ldots , {u^i}_{\sigma }}\}.$
Applying the analysis above to
![]() $T_{{\boldsymbol {\alpha }}^1,V},\dots ,T_{{\boldsymbol {\alpha }}^{\Delta },V}$
, we obtain that
$T_{{\boldsymbol {\alpha }}^1,V},\dots ,T_{{\boldsymbol {\alpha }}^{\Delta },V}$
, we obtain that
![]() $\operatorname {span}\{{b_{P,1}, \cdots b_{P,\Delta }}\}\subseteq \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$
. As
$\operatorname {span}\{{b_{P,1}, \cdots b_{P,\Delta }}\}\subseteq \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$
. As
![]() ${\boldsymbol {\alpha }}^1,\dots {\boldsymbol {\alpha }}^{\Delta }$
are linearly independent, we have that
${\boldsymbol {\alpha }}^1,\dots {\boldsymbol {\alpha }}^{\Delta }$
are linearly independent, we have that
![]() $\{{{a}_1,\ldots , {a}_{\Delta }}\} \subset \operatorname {span}\{{b_{P,1}, \cdots b_{P,\Delta }}\}$
, and thus
$\{{{a}_1,\ldots , {a}_{\Delta }}\} \subset \operatorname {span}\{{b_{P,1}, \cdots b_{P,\Delta }}\}$
, and thus
![]() $\text {Lin}(P) \subseteq V + \lbrace {a}_1,\ldots , {a}_{\Delta }\rbrace + \text {Lin}(P') \subseteq V + \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$
.
$\text {Lin}(P) \subseteq V + \lbrace {a}_1,\ldots , {a}_{\Delta }\rbrace + \text {Lin}(P') \subseteq V + \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$
.
3 Structure theorem for quadratics satisfying
 $ \prod _i Q_i \in \sqrt {(A,B)}$
$ \prod _i Q_i \in \sqrt {(A,B)}$
An important tool in the proofs of our main results is Theorem 1.5 that classifies all the possible cases in which a product of quadratic polynomials
![]() $Q_1\cdot Q_2\cdot \ldots \cdot Q_k$
is in the radical of two other quadratics,
$Q_1\cdot Q_2\cdot \ldots \cdot Q_k$
is in the radical of two other quadratics,
![]() $\sqrt {\left \langle {A,B}\right \rangle }$
. To ease the reading, we repeat the statement of the theorem here, albeit with slightly different notation.
$\sqrt {\left \langle {A,B}\right \rangle }$
. To ease the reading, we repeat the statement of the theorem here, albeit with slightly different notation.
Theorem 3.1. Let
![]() $\{Q_k\}_{k\in {\mathcal {K}}},A,B$
be homogeneous polynomials of degree
$\{Q_k\}_{k\in {\mathcal {K}}},A,B$
be homogeneous polynomials of degree
![]() $2$
such that
$2$
such that
![]() $\prod _{k\in {\mathcal {K}}}Q_k \in \sqrt {\left \langle {A,B}\right \rangle }$
. Then one of the following cases hold:
$\prod _{k\in {\mathcal {K}}}Q_k \in \sqrt {\left \langle {A,B}\right \rangle }$
. Then one of the following cases hold:
-
(prime-case): There is
 $k\in {\mathcal {K}}$
such that
$k\in {\mathcal {K}}$
such that
 $Q_k$
is in the linear span of
$Q_k$
is in the linear span of
 $A,B$
.
$A,B$
. -
(product-case): There exists a nontrivial linear combination of the form
 $\alpha A+\beta B = c\cdot d$
, where c and d are linear forms.
$\alpha A+\beta B = c\cdot d$
, where c and d are linear forms. -
(linear-case): There exist two linear forms c and d such that when setting
 $c=d=0$
we get that
$c=d=0$
we get that
 $A,B$
and one of
$A,B$
and one of
 $\{Q_k\}_{k\in {\mathcal {K}}}$
vanish.
$\{Q_k\}_{k\in {\mathcal {K}}}$
vanish.
The following claim of [Reference Gupta12] shows that we can assume
![]() $|{\mathcal {K}}| = 4$
in the statement of Theorem 3.1.
$|{\mathcal {K}}| = 4$
in the statement of Theorem 3.1.
Claim 3.2 (Claim 11 in [Reference Gupta12]).
Let
![]() ${P}_1,\ldots , {P}_{d},{Q}_1,\ldots , {Q}_{k}\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be homogeneous and the degree of each
${P}_1,\ldots , {P}_{d},{Q}_1,\ldots , {Q}_{k}\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be homogeneous and the degree of each
![]() $P_i$
is at most r. Then,
$P_i$
is at most r. Then,
 $$ \begin{align*} \prod_{i=1}^k Q_i \in \sqrt{\left \langle{{P}_1,\ldots, {P}_{d}}\right \rangle} \Rightarrow \exists \lbrace {i}_1,\ldots, {i}_{r^d} \rbrace \subset [k] \; \text{ such that} \quad \prod_{j=1}^{r^d} Q_{i_j} \in \sqrt{\left \langle{{P}_1,\ldots, {P}_{d}}\right \rangle} . \end{align*} $$
$$ \begin{align*} \prod_{i=1}^k Q_i \in \sqrt{\left \langle{{P}_1,\ldots, {P}_{d}}\right \rangle} \Rightarrow \exists \lbrace {i}_1,\ldots, {i}_{r^d} \rbrace \subset [k] \; \text{ such that} \quad \prod_{j=1}^{r^d} Q_{i_j} \in \sqrt{\left \langle{{P}_1,\ldots, {P}_{d}}\right \rangle} . \end{align*} $$
Thus, for
![]() $r=d=2$
it follow that there are at most four polynomials among the
$r=d=2$
it follow that there are at most four polynomials among the
![]() $Q_i$
s whose product is in
$Q_i$
s whose product is in
![]() $\sqrt {\left \langle {A,B}\right \rangle }$
.
$\sqrt {\left \langle {A,B}\right \rangle }$
.
Before proving Theorem 3.1, we explain the intuition behind the different cases in the theorem. Clearly, if one of
![]() $Q_1,\ldots ,Q_4$
is a linear combination of
$Q_1,\ldots ,Q_4$
is a linear combination of
![]() $A,B$
, then it is in their radical (and in fact, in their linear span). If A and B span a product of the form
$A,B$
, then it is in their radical (and in fact, in their linear span). If A and B span a product of the form
![]() $ab$
, then, say,
$ab$
, then, say,
![]() $(A+ac)(A+bd)$
is in their radical. Indeed,
$(A+ac)(A+bd)$
is in their radical. Indeed,
![]() $\sqrt {\left \langle {A,B}\right \rangle } = \sqrt {\left \langle {A,ab}\right \rangle }$
. This case is clearly different than the linear span case. Finally, we note that, if
$\sqrt {\left \langle {A,B}\right \rangle } = \sqrt {\left \langle {A,ab}\right \rangle }$
. This case is clearly different than the linear span case. Finally, we note that, if
![]() $A=ac+bd$
and
$A=ac+bd$
and
![]() $B=ae+bf$
, then the product
$B=ae+bf$
, then the product
![]() $a\cdot b\cdot (cf-de)$
is in
$a\cdot b\cdot (cf-de)$
is in
![]() $\sqrt {\left \langle {A,B}\right \rangle }$
.Footnote
4
This case is different than the other two cases as A and B do not span any linear form (or any reducible quadratic) non trivially.
$\sqrt {\left \langle {A,B}\right \rangle }$
.Footnote
4
This case is different than the other two cases as A and B do not span any linear form (or any reducible quadratic) non trivially.
Thus, all the three cases are distinct and can happen. What Theorem 3.1 shows is that, essentially, these are the only possible cases.
Proof of Theorem 3.1.
Following Theorem 3.2, we shall assume in the proof that
![]() $|{\mathcal {K}}|=4$
. By applying a suitable linear transformation, we can assume that for some
$|{\mathcal {K}}|=4$
. By applying a suitable linear transformation, we can assume that for some
![]() $r\geq 1$
$r\geq 1$
 $$ \begin{align*} A = \sum_{i=1}^{r} x_i^2. \end{align*} $$
$$ \begin{align*} A = \sum_{i=1}^{r} x_i^2. \end{align*} $$
We can also assume without loss of generality that
![]() $x_1^2$
appears only in A as we can replace B with any polynomial of the form
$x_1^2$
appears only in A as we can replace B with any polynomial of the form
![]() $B'=B - \alpha A$
without affecting the result as
$B'=B - \alpha A$
without affecting the result as
![]() $\left \langle {A,B}\right \rangle = \left \langle {A,B'}\right \rangle $
. Furthermore, all cases in the theorem remain the same if we replace B with
$\left \langle {A,B}\right \rangle = \left \langle {A,B'}\right \rangle $
. Furthermore, all cases in the theorem remain the same if we replace B with
![]() $B'$
and vice versa.
$B'$
and vice versa.
In a similar fashion, we can replace
![]() $Q_1$
with
$Q_1$
with
![]() $Q_1'=Q_1-\alpha A$
to get rid of the term
$Q_1'=Q_1-\alpha A$
to get rid of the term
![]() $x_1^2$
in
$x_1^2$
in
![]() $Q_1$
. We can do the same for the other
$Q_1$
. We can do the same for the other
![]() $Q_i$
s. Thus, without loss of generality, the situation is
$Q_i$
s. Thus, without loss of generality, the situation is
 $$ \begin{align} \begin{aligned} A &= x_1^2 - A' \\ B &= x_1\cdot b - B' \ \\ Q_i &= x_1 \cdot b_i - Q^{\prime}_i \quad \text{for} \quad i\in\{1,2,3,4\}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} A &= x_1^2 - A' \\ B &= x_1\cdot b - B' \ \\ Q_i &= x_1 \cdot b_i - Q^{\prime}_i \quad \text{for} \quad i\in\{1,2,3,4\}, \end{aligned} \end{align} $$
where
![]() $A',b,B',Q^{\prime }_i,b_i$
are homogeneous polynomials that do not depend on
$A',b,B',Q^{\prime }_i,b_i$
are homogeneous polynomials that do not depend on
![]() $x_1$
, the polynomials
$x_1$
, the polynomials
![]() $A',B',Q'$
have degree
$A',B',Q'$
have degree
![]() $\leq 2$
and
$\leq 2$
and
![]() $b,b_i$
are linear forms. The analysis shall deal with two cases according to whether B depends on
$b,b_i$
are linear forms. The analysis shall deal with two cases according to whether B depends on
![]() $x_1$
or not, as we only consider the resultant of A and B with respect to
$x_1$
or not, as we only consider the resultant of A and B with respect to
![]() $x_1$
when it appears in both polynomials.
$x_1$
when it appears in both polynomials.
Case
![]() $\boldsymbol{b \not \equiv 0}$
:
$\boldsymbol{b \not \equiv 0}$
:
Consider the resultant of A and B with respect to
![]() $x_1$
. It is easy to see that
$x_1$
. It is easy to see that
We first prove that, if the resultant is irreducible, then Case (prime-case) of Theorem 3.1 holds. For this, we shall need the following claim.
Claim 3.3. Whenever
![]() $\mathrm {Res}_{x_1}(A,B) =0$
, it holds that
$\mathrm {Res}_{x_1}(A,B) =0$
, it holds that
![]() $\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i) =0$
.
$\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i) =0$
.
Proof. Let
![]() ${\boldsymbol {\alpha }} \in \mathbb {C}^{n-1}$
be such that
${\boldsymbol {\alpha }} \in \mathbb {C}^{n-1}$
be such that
![]() $\mathrm {Res}_{x_1}(A,B)({\boldsymbol {\alpha }})=0$
then either
$\mathrm {Res}_{x_1}(A,B)({\boldsymbol {\alpha }})=0$
then either
![]() $b({\boldsymbol {\alpha }})=0$
, which also implies
$b({\boldsymbol {\alpha }})=0$
, which also implies
![]() $B'({\boldsymbol {\alpha }})=0$
and in this case the claim clearly holds, or
$B'({\boldsymbol {\alpha }})=0$
and in this case the claim clearly holds, or
![]() $b({\boldsymbol {\alpha }})\neq 0$
. Consider the case
$b({\boldsymbol {\alpha }})\neq 0$
. Consider the case
![]() $b({\boldsymbol {\alpha }})\neq 0$
, and set
$b({\boldsymbol {\alpha }})\neq 0$
, and set
![]() $x_1=B'({\boldsymbol {\alpha }})/b({\boldsymbol {\alpha }})$
(we are free to select a value for
$x_1=B'({\boldsymbol {\alpha }})/b({\boldsymbol {\alpha }})$
(we are free to select a value for
![]() $x_1$
as
$x_1$
as
![]() $\mathrm {Res}_{x_1}(A,B)$
does not involve
$\mathrm {Res}_{x_1}(A,B)$
does not involve
![]() $x_1$
). Notice that for this substitution we have that
$x_1$
). Notice that for this substitution we have that
![]() $B({\boldsymbol {\alpha }})=0$
and that
$B({\boldsymbol {\alpha }})=0$
and that
Hence, we also have
![]() $\prod _{i=1}^{4}Q_i |_{x_1=B'({\boldsymbol {\alpha }})/b({\boldsymbol {\alpha }})} = 0$
. In other words that
$\prod _{i=1}^{4}Q_i |_{x_1=B'({\boldsymbol {\alpha }})/b({\boldsymbol {\alpha }})} = 0$
. In other words that
 $$ \begin{align*} \left(\frac{1}{b^4}\prod_{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime}_i)\right)({\boldsymbol{\alpha}})=0 .\\[-49pt] \end{align*} $$
$$ \begin{align*} \left(\frac{1}{b^4}\prod_{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime}_i)\right)({\boldsymbol{\alpha}})=0 .\\[-49pt] \end{align*} $$
It follows that
 $$ \begin{align*} \prod_{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime}_i) \in \sqrt{\mathrm{Res}_{x_1}(A,B)} . \end{align*} $$
$$ \begin{align*} \prod_{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime}_i) \in \sqrt{\mathrm{Res}_{x_1}(A,B)} . \end{align*} $$
In other words, for some positive integer k we have that
![]() $\mathrm {Res}_{x_1}(A,B)$
divides
$\mathrm {Res}_{x_1}(A,B)$
divides
![]() $\left (\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i)\right )^k$
. As every irreducible factor of
$\left (\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i)\right )^k$
. As every irreducible factor of
![]() $\left (\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i)\right )^k$
is of degree
$\left (\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i)\right )^k$
is of degree
![]() $3$
or less, we get that, if the resultant is irreducible, then one of the multiplicands must be identically zero. Assume without loss of generality that
$3$
or less, we get that, if the resultant is irreducible, then one of the multiplicands must be identically zero. Assume without loss of generality that
![]() $B'b_1-bB^{\prime }_1=0$
. It is not hard to verify that in this case either
$B'b_1-bB^{\prime }_1=0$
. It is not hard to verify that in this case either
![]() $Q_1$
is a scalar multiple of B and then Theorem 3.1(prime-case) holds, or that
$Q_1$
is a scalar multiple of B and then Theorem 3.1(prime-case) holds, or that
![]() $B'$
is divisible by b. However, in the latter case it also holds that b divides the resultant, contradicting the assumption that it is irreducible.
$B'$
is divisible by b. However, in the latter case it also holds that b divides the resultant, contradicting the assumption that it is irreducible.
From now on we assume that
![]() $\mathrm {Res}_{x_1}(A,B)$
is reducible. We consider two possibilities. Either
$\mathrm {Res}_{x_1}(A,B)$
is reducible. We consider two possibilities. Either
![]() $\mathrm {Res}_{x_1}(A,B)$
has a linear factor or it can be written as
$\mathrm {Res}_{x_1}(A,B)$
has a linear factor or it can be written as
for irreducible quadratic polynomials C and D.
Consider the case where the resultant has a linear factor. If that linear factor is b, then b also divides B and Theorem 3.1(product-case) holds. Otherwise, if it is a different linear form
![]() $\ell $
, then when setting
$\ell $
, then when setting
![]() $\ell =0$
we get that the resultant of
$\ell =0$
we get that the resultant of
![]() $A|_{\ell =0}$
and
$A|_{\ell =0}$
and
![]() $B|_{\ell =0}$
is zero, and hence, either
$B|_{\ell =0}$
is zero, and hence, either
![]() $B|_{\ell =0}$
is identically zero and Theorem 3.1(product-case) holds or they share a common factor (see Theorem 2.11). It is not hard to see that, if that common factor is of degree
$B|_{\ell =0}$
is identically zero and Theorem 3.1(product-case) holds or they share a common factor (see Theorem 2.11). It is not hard to see that, if that common factor is of degree
![]() $2$
, then Theorem 3.1(product-case) holds, and if it is a linear factor, then Theorem 3.1(linear-case) holds.
$2$
, then Theorem 3.1(product-case) holds, and if it is a linear factor, then Theorem 3.1(linear-case) holds.
Thus, the only case left to handle (when
![]() $b\not \equiv 0$
) is when there are two irreducible quadratic polynomials, C and D, such that
$b\not \equiv 0$
) is when there are two irreducible quadratic polynomials, C and D, such that
![]() $CD=\mathrm {Res}_{x_1}(A,B)$
. As C and D divide two multiplicands in
$CD=\mathrm {Res}_{x_1}(A,B)$
. As C and D divide two multiplicands in
![]() $\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i) $
, we can assume, without loss of generality, that
$\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i) $
, we can assume, without loss of generality, that
![]() $(B'\cdot b_3 - b\cdot Q^{\prime }_3)\cdot (B'\cdot b_4 - b\cdot Q^{\prime }_4) \in \sqrt {\left \langle {\mathrm {Res}_{x_1}(A,B)}\right \rangle } $
. Next, we express
$(B'\cdot b_3 - b\cdot Q^{\prime }_3)\cdot (B'\cdot b_4 - b\cdot Q^{\prime }_4) \in \sqrt {\left \langle {\mathrm {Res}_{x_1}(A,B)}\right \rangle } $
. Next, we express
![]() $A',B',C$
and D as quadratics over b. That is,
$A',B',C$
and D as quadratics over b. That is,
 $$ \begin{align} A' &= \alpha b^2 + a_1 b + A" \\ B' &= \beta b^2 + a_2 b + B"\nonumber \\ C &= \gamma b^2 + a_3 b + C" \nonumber \\ D &= \delta b^2 + a_4 b + D",\nonumber \end{align} $$
$$ \begin{align} A' &= \alpha b^2 + a_1 b + A" \\ B' &= \beta b^2 + a_2 b + B"\nonumber \\ C &= \gamma b^2 + a_3 b + C" \nonumber \\ D &= \delta b^2 + a_4 b + D",\nonumber \end{align} $$
where
![]() $a_1,\ldots ,D"$
do not involve b (nor
$a_1,\ldots ,D"$
do not involve b (nor
![]() $x_1$
). We have the following two representations of the resultant:
$x_1$
). We have the following two representations of the resultant:
 $$ \begin{align} \mathrm{Res}_{x_1}(A,B)&= {B'}^2 - b^2 \cdot A' \\ &= \beta^2\cdot b^4 + 2\beta a_2 \cdot b^3 + (2\beta B" + a_2^2) \cdot b^2 + 2a_2B" \cdot b + {B"}^2 - \alpha b^4- a_1 b^3 - A" b^2 \nonumber \\ &= (\beta^2-\alpha)b^4 + (2\beta a_2 - a_1)\cdot b^3 + (2\beta B" + a_2^2- A") \cdot b^2 + 2a_2B" \cdot b + {B"}^2 \nonumber \end{align} $$
$$ \begin{align} \mathrm{Res}_{x_1}(A,B)&= {B'}^2 - b^2 \cdot A' \\ &= \beta^2\cdot b^4 + 2\beta a_2 \cdot b^3 + (2\beta B" + a_2^2) \cdot b^2 + 2a_2B" \cdot b + {B"}^2 - \alpha b^4- a_1 b^3 - A" b^2 \nonumber \\ &= (\beta^2-\alpha)b^4 + (2\beta a_2 - a_1)\cdot b^3 + (2\beta B" + a_2^2- A") \cdot b^2 + 2a_2B" \cdot b + {B"}^2 \nonumber \end{align} $$
and
 $$ \begin{align} \mathrm{Res}_{x_1}(Q_1,Q_2)&=CD \\ &= (\gamma b^2 + a_3 b + C")\cdot (\delta b^2 + a_4 b + D")\nonumber \\ &= \gamma\delta b^4 + (\gamma a_4 + \delta a_3)b^3 + (\gamma D" + a_3 a_4 + \delta C")b^2 + (a_3D" + a_4C")b + C"D" .\nonumber \end{align} $$
$$ \begin{align} \mathrm{Res}_{x_1}(Q_1,Q_2)&=CD \\ &= (\gamma b^2 + a_3 b + C")\cdot (\delta b^2 + a_4 b + D")\nonumber \\ &= \gamma\delta b^4 + (\gamma a_4 + \delta a_3)b^3 + (\gamma D" + a_3 a_4 + \delta C")b^2 + (a_3D" + a_4C")b + C"D" .\nonumber \end{align} $$
Comparing the different coefficients of b in the two representations in equations (3.3) and (3.4), we obtain the following equalities:
We now consider the two possible cases giving equation (3.5).
-
1. Case 1 explaining equation (3.5): After rescaling C and D, we have that
 ${B"}=C"=D"$
. Equation (3.2) implies that for some linear form
${B"}=C"=D"$
. Equation (3.2) implies that for some linear form
 $u,v$
we have that
$u,v$
we have that  $$ \begin{align*} C = bv + B' \quad \text{and} \quad D = bu+B'. \end{align*} $$
$$ \begin{align*} C = bv + B' \quad \text{and} \quad D = bu+B'. \end{align*} $$
We now expand the resultant again:
 $$ \begin{align*} {B'}^2 + b(v+u)B' + b^2 vu=(bv + B')\cdot ( bu+B') &= CD \\ &= \mathrm{Res}_{x_1}(A,B)= {B'}^2 - b^2 A'. \end{align*} $$
$$ \begin{align*} {B'}^2 + b(v+u)B' + b^2 vu=(bv + B')\cdot ( bu+B') &= CD \\ &= \mathrm{Res}_{x_1}(A,B)= {B'}^2 - b^2 A'. \end{align*} $$
Hence,
(3.7) $$ \begin{align} (v+u)B' + b vu=- b A' . \end{align} $$
$$ \begin{align} (v+u)B' + b vu=- b A' . \end{align} $$
Thus, either b divides
 $B'$
in which case we get that b divides B and we are done as Theorem 3.1 (product-case) holds, or b divides
$B'$
in which case we get that b divides B and we are done as Theorem 3.1 (product-case) holds, or b divides
 $u+v$
. That is, (3.8)
$u+v$
. That is, (3.8) $$ \begin{align} u+v = \varepsilon b \end{align} $$
$$ \begin{align} u+v = \varepsilon b \end{align} $$
for some constant
 $\varepsilon \in \mathbb {C}$
. Plugging this back into equation (3.7), we get
$\varepsilon \in \mathbb {C}$
. Plugging this back into equation (3.7), we get  $$ \begin{align*} \varepsilon b B' + b vu=- b A' . \end{align*} $$
$$ \begin{align*} \varepsilon b B' + b vu=- b A' . \end{align*} $$
In other words,
 $$ \begin{align*} \varepsilon B' + vu= - A' . \end{align*} $$
$$ \begin{align*} \varepsilon B' + vu= - A' . \end{align*} $$
Consider the linear combination
 $Q=A + \varepsilon B$
. We get that (3.9)
$Q=A + \varepsilon B$
. We get that (3.9) $$ \begin{align} Q=A + \varepsilon B &= (x_1^2 - A') + \varepsilon (x_1 b-B') \nonumber \\ &= x_1^2 + \varepsilon x_1 b + vu \nonumber \\ &= x_1^2 + x_1(u+v)+uv \nonumber\\ &= (x_1+u)(x_1+v), \end{align} $$
$$ \begin{align} Q=A + \varepsilon B &= (x_1^2 - A') + \varepsilon (x_1 b-B') \nonumber \\ &= x_1^2 + \varepsilon x_1 b + vu \nonumber \\ &= x_1^2 + x_1(u+v)+uv \nonumber\\ &= (x_1+u)(x_1+v), \end{align} $$
where the equality in the third line follows from equation (3.8). Thus, equation (3.9) shows that some linear combination of A and B is reducible which implies that Theorem 3.1(product-case) holds.
-
2. Case 2 explaining equation (3.5):
 ${B"} = u\cdot v$
and we have that, without loss of generality,
${B"} = u\cdot v$
and we have that, without loss of generality,
 $C"=u^2$
and
$C"=u^2$
and
 $D"=v^2$
(where
$D"=v^2$
(where
 $u,v$
are linear forms). Consider equation (3.6). We have that v divides
$u,v$
are linear forms). Consider equation (3.6). We have that v divides
 $2a_2B" - a_3D"$
. It follows that v is also a factor of
$2a_2B" - a_3D"$
. It follows that v is also a factor of
 $ a_4C" $
. Thus, either u is a multiple of v and we are back in the case where
$ a_4C" $
. Thus, either u is a multiple of v and we are back in the case where
 $C"$
and
$C"$
and
 $D"$
are multiples of each other, or
$D"$
are multiples of each other, or
 $a_4$
is a multiple of v. In this case, we get from equation (3.2) that for some constant
$a_4$
is a multiple of v. In this case, we get from equation (3.2) that for some constant
 $\delta '$
,
$\delta '$
,  $$ \begin{align*} D = \delta b^2 + a_4 b + D" = \delta b^2 +\delta' v b + v^2. \end{align*} $$
$$ \begin{align*} D = \delta b^2 + a_4 b + D" = \delta b^2 +\delta' v b + v^2. \end{align*} $$
Thus, D is a homogeneous polynomial in two linear forms. Hence, D is reducible, in contradiction.
This concludes the proof of Theorem 3.1 for the case
![]() $b\not \equiv 0$
.
$b\not \equiv 0$
.
Case
![]() $\boldsymbol{b \equiv 0}$
:
$\boldsymbol{b \equiv 0}$
:
To ease notation, let use denote
![]() $x=x_1$
. We have that
$x=x_1$
. We have that
![]() $A = x^2 - A' $
and that x does not appear in
$A = x^2 - A' $
and that x does not appear in
![]() $A',B$
. Let y be some variable such that
$A',B$
. Let y be some variable such that
![]() $B=y^2-B'$
, and
$B=y^2-B'$
, and
![]() $B'$
does not involve y (we can always assume this is the case without loss of generality). As before, we can subtract a multiple of B from A so that the term
$B'$
does not involve y (we can always assume this is the case without loss of generality). As before, we can subtract a multiple of B from A so that the term
![]() $y^2$
does not appear in A. If A still involves y, then we are back in the previous case (treating y as the variable according to which we take the resultant). Thus, the only case left to study is when there are two variables x and y such that
$y^2$
does not appear in A. If A still involves y, then we are back in the previous case (treating y as the variable according to which we take the resultant). Thus, the only case left to study is when there are two variables x and y such that
where neither
![]() $A'$
nor
$A'$
nor
![]() $B'$
involve either x or y. To ease notation, denote the rest of the variables as
$B'$
involve either x or y. To ease notation, denote the rest of the variables as
![]() ${\mathbf {z}}$
. Thus,
${\mathbf {z}}$
. Thus,
![]() $A'=A'({\mathbf {z}})$
and
$A'=A'({\mathbf {z}})$
and
![]() $B'=B'({\mathbf {z}})$
. It is immediate that for any assignment to
$B'=B'({\mathbf {z}})$
. It is immediate that for any assignment to
![]() ${\mathbf {z}}$
there is an assignment to
${\mathbf {z}}$
there is an assignment to
![]() $x,y$
that yields a common zero of
$x,y$
that yields a common zero of
![]() $A,B$
.
$A,B$
.
By subtracting linear combinations of A and B from the
![]() $Q_i$
s, we can assume that for every
$Q_i$
s, we can assume that for every
![]() $i\in [4]$
$i\in [4]$
We next show that, under the assumptions in the theorem’s statement, it must be the case that either
![]() $A'$
or
$A'$
or
![]() $B'$
is a perfect square or that
$B'$
is a perfect square or that
![]() $A'\sim B'$
. In either situation, we have that Theorem 3.1(product-case) holds. We first show that, if
$A'\sim B'$
. In either situation, we have that Theorem 3.1(product-case) holds. We first show that, if
![]() $A'$
and
$A'$
and
![]() $B'$
are linearly independent, then this implies that at least one of
$B'$
are linearly independent, then this implies that at least one of
![]() $A',B'$
is a perfect square.
$A',B'$
is a perfect square.
Let
![]() $Z(A,B)$
be the set of common zeros of A and B, and denote by
$Z(A,B)$
be the set of common zeros of A and B, and denote by
![]() $\pi _{{\mathbf {z}}}: Z(A,B) \rightarrow \mathbb {C}^{n-2}$
, the projection on the
$\pi _{{\mathbf {z}}}: Z(A,B) \rightarrow \mathbb {C}^{n-2}$
, the projection on the
![]() ${\mathbf {z}}$
coordinates. Note that
${\mathbf {z}}$
coordinates. Note that
![]() $\pi _{{\mathbf {z}}}$
is surjective; as for any assignment to
$\pi _{{\mathbf {z}}}$
is surjective; as for any assignment to
![]() ${\mathbf {z}}$
, there is an assignment to
${\mathbf {z}}$
, there is an assignment to
![]() $x,y$
that yields a common zero of
$x,y$
that yields a common zero of
![]() $A,B$
.
$A,B$
.
Claim 3.4. Let
![]() $Z(A,B) = \bigcup _{i=1}^k X_k$
be the decomposition of
$Z(A,B) = \bigcup _{i=1}^k X_k$
be the decomposition of
![]() $Z(A,B)$
to irreducible components. Then there exists
$Z(A,B)$
to irreducible components. Then there exists
![]() $i\in [k]$
such that
$i\in [k]$
such that
![]() $\pi _{{\mathbf {z}}}(X_i)$
is dense in
$\pi _{{\mathbf {z}}}(X_i)$
is dense in
![]() $\mathbb {C}^{n-2}$
.
$\mathbb {C}^{n-2}$
.
Proof.
![]() $\bigcup _{i=1}^k \pi _{{\mathbf {z}}}( X_i) = \pi _{{\mathbf {z}}}(Z(A,B)) = \mathbb {C}^{n-2}$
, as
$\bigcup _{i=1}^k \pi _{{\mathbf {z}}}( X_i) = \pi _{{\mathbf {z}}}(Z(A,B)) = \mathbb {C}^{n-2}$
, as
![]() $\pi _{{\mathbf {z}}}$
is a surjection, it holds that
$\pi _{{\mathbf {z}}}$
is a surjection, it holds that
![]() $\bigcup _{i=1}^k \overline {\pi _{{\mathbf {z}}}( X_i)} = \mathbb {C}^{n-2}$
. We also know that
$\bigcup _{i=1}^k \overline {\pi _{{\mathbf {z}}}( X_i)} = \mathbb {C}^{n-2}$
. We also know that
![]() $\mathbb {C}^{n-2}$
is irreducible, and thus, there is
$\mathbb {C}^{n-2}$
is irreducible, and thus, there is
![]() $i\in [k]$
such that
$i\in [k]$
such that
![]() $\overline {\pi _{{\mathbf {z}}}( X_i)} = \mathbb {C}^{n-2}$
, which implies that
$\overline {\pi _{{\mathbf {z}}}( X_i)} = \mathbb {C}^{n-2}$
, which implies that
![]() ${\pi _{{\mathbf {z}}}( X_i)} $
is dense.
${\pi _{{\mathbf {z}}}( X_i)} $
is dense.
Assume, without loss of generality, that
![]() $\pi _{{\mathbf {z}}}( X_1)$
is dense. We know that
$\pi _{{\mathbf {z}}}( X_1)$
is dense. We know that
![]() $X_1 \subseteq Z(\prod _{i=1}^{4}Q_i)$
, so we can assume, without loss of generality, that
$X_1 \subseteq Z(\prod _{i=1}^{4}Q_i)$
, so we can assume, without loss of generality, that
![]() $X_1 \subseteq Z(Q_1)$
. Observe that this implies that
$X_1 \subseteq Z(Q_1)$
. Observe that this implies that
![]() $Q_1$
must depend on at least one of
$Q_1$
must depend on at least one of
![]() $x,y$
. Indeed, if
$x,y$
. Indeed, if
![]() $Q_1$
depends on neither, then it is a polynomial in
$Q_1$
depends on neither, then it is a polynomial in
![]() ${\mathbf {z}}$
, and hence, its set of zeros cannot be dense.
${\mathbf {z}}$
, and hence, its set of zeros cannot be dense.
Every point
![]() $\boldsymbol {\xi } \in X_1$
is of the form
$\boldsymbol {\xi } \in X_1$
is of the form
![]() $\boldsymbol {\xi } = (\delta _1\sqrt {A'({\boldsymbol {\beta }})},\delta _2\sqrt {B'({\boldsymbol {\beta }})},{\boldsymbol {\beta }})$
, for some
$\boldsymbol {\xi } = (\delta _1\sqrt {A'({\boldsymbol {\beta }})},\delta _2\sqrt {B'({\boldsymbol {\beta }})},{\boldsymbol {\beta }})$
, for some
![]() ${\boldsymbol {\beta }} \in \mathbb {C}^{n-2}$
,
${\boldsymbol {\beta }} \in \mathbb {C}^{n-2}$
,
![]() $\delta _1,\delta _2 \in \{\pm 1\}$
(
$\delta _1,\delta _2 \in \{\pm 1\}$
(
![]() $ \delta _1,\delta _2$
may be functions of
$ \delta _1,\delta _2$
may be functions of
![]() ${\boldsymbol {\beta }}$
). Thus,
${\boldsymbol {\beta }}$
). Thus,
![]() $Q_1(\boldsymbol {\xi }) = Q_1(\delta _1\sqrt {A'({\boldsymbol {\beta }})},\delta _2\sqrt {B'({\boldsymbol {\beta }})},{\boldsymbol {\beta }}) =0$
, and we obtain that
$Q_1(\boldsymbol {\xi }) = Q_1(\delta _1\sqrt {A'({\boldsymbol {\beta }})},\delta _2\sqrt {B'({\boldsymbol {\beta }})},{\boldsymbol {\beta }}) =0$
, and we obtain that
As we assumed that
![]() $Q_1$
depends on at least one of
$Q_1$
depends on at least one of
![]() $x,y$
, let us assume without loss of generality that either
$x,y$
, let us assume without loss of generality that either
![]() $\alpha _1$
or
$\alpha _1$
or
![]() $a_1$
are nonzero. The next argument is similar to the proof that
$a_1$
are nonzero. The next argument is similar to the proof that
![]() $\sqrt {2}$
is irrational. Note that we use the fact that
$\sqrt {2}$
is irrational. Note that we use the fact that
![]() $\delta _1^2=\delta _2^2=1$
.
$\delta _1^2=\delta _2^2=1$
.
 $$ \begin{align} (3.10) \implies & B'({\boldsymbol{\beta}}')\left( \alpha_1 \delta_1 \sqrt{A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}') \right)^2 = \left( Q^{\prime}_1({\boldsymbol{\beta}}') +a_1({\boldsymbol{\beta}}') \delta_1 \sqrt{A'({\boldsymbol{\beta}}')} \right)^2 \nonumber \\ \implies & B'({\boldsymbol{\beta}}')\left( \alpha_1^2 {A'({\boldsymbol{\beta}}')} +2\delta_1\alpha_1 b_1({\boldsymbol{\beta}}') \sqrt{A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}')^2 \right) = \nonumber \\ & \quad\quad\quad Q^{\prime}_1({\boldsymbol{\beta}}')^2 + 2\delta_1 a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \sqrt{A'({\boldsymbol{\beta}}')} + a_1({\boldsymbol{\beta}}')^2 {A'({\boldsymbol{\beta}}')} \nonumber \\ \implies &\delta_1 \sqrt{A'({\boldsymbol{\beta}}')}\left( 2\alpha_1 b_1({\boldsymbol{\beta}}') B'({\boldsymbol{\beta}}') - 2a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \right) = \end{align} $$
$$ \begin{align} (3.10) \implies & B'({\boldsymbol{\beta}}')\left( \alpha_1 \delta_1 \sqrt{A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}') \right)^2 = \left( Q^{\prime}_1({\boldsymbol{\beta}}') +a_1({\boldsymbol{\beta}}') \delta_1 \sqrt{A'({\boldsymbol{\beta}}')} \right)^2 \nonumber \\ \implies & B'({\boldsymbol{\beta}}')\left( \alpha_1^2 {A'({\boldsymbol{\beta}}')} +2\delta_1\alpha_1 b_1({\boldsymbol{\beta}}') \sqrt{A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}')^2 \right) = \nonumber \\ & \quad\quad\quad Q^{\prime}_1({\boldsymbol{\beta}}')^2 + 2\delta_1 a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \sqrt{A'({\boldsymbol{\beta}}')} + a_1({\boldsymbol{\beta}}')^2 {A'({\boldsymbol{\beta}}')} \nonumber \\ \implies &\delta_1 \sqrt{A'({\boldsymbol{\beta}}')}\left( 2\alpha_1 b_1({\boldsymbol{\beta}}') B'({\boldsymbol{\beta}}') - 2a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \right) = \end{align} $$
 $$ \begin{align} & \quad\quad\quad Q^{\prime}_1({\boldsymbol{\beta}}')^2 +a_1({\boldsymbol{\beta}}')^2 {A'({\boldsymbol{\beta}}')} -B'({\boldsymbol{\beta}}')\left( \alpha_1^2 {A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}')^2 \right)\nonumber \\ \qquad\ \!\implies & A'({\boldsymbol{\beta}}') \left( 2\alpha_1 b_1({\boldsymbol{\beta}}') B'({\boldsymbol{\beta}}') - 2a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \right)^2 = \end{align} $$
$$ \begin{align} & \quad\quad\quad Q^{\prime}_1({\boldsymbol{\beta}}')^2 +a_1({\boldsymbol{\beta}}')^2 {A'({\boldsymbol{\beta}}')} -B'({\boldsymbol{\beta}}')\left( \alpha_1^2 {A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}')^2 \right)\nonumber \\ \qquad\ \!\implies & A'({\boldsymbol{\beta}}') \left( 2\alpha_1 b_1({\boldsymbol{\beta}}') B'({\boldsymbol{\beta}}') - 2a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \right)^2 = \end{align} $$
This equality holds for every
![]() ${\boldsymbol {\beta }} \in \pi _{{\mathbf {z}}}(X_1)$
, which is a dense set, and hence holds as a polynomial identity. Thus, either
${\boldsymbol {\beta }} \in \pi _{{\mathbf {z}}}(X_1)$
, which is a dense set, and hence holds as a polynomial identity. Thus, either
![]() $A'({\mathbf {z}})$
is a square, in which case we are done or it must be the case that the following identities hold
$A'({\mathbf {z}})$
is a square, in which case we are done or it must be the case that the following identities hold
and
By symmetry, if
![]() $B'({\mathbf {z}})$
is not a square (as otherwise we are done), we get that
$B'({\mathbf {z}})$
is not a square (as otherwise we are done), we get that
If
![]() $\alpha _1=0$
, then we get from (3.14) that
$\alpha _1=0$
, then we get from (3.14) that
![]() $Q^{\prime }_1\equiv 0$
. Hence, by (3.13),
$Q^{\prime }_1\equiv 0$
. Hence, by (3.13),
Since we assumed that
![]() $A'$
and
$A'$
and
![]() $B'$
are independent, this implies that
$B'$
are independent, this implies that
![]() $A'$
and
$A'$
and
![]() $B'$
are both squares. If
$B'$
are both squares. If
![]() $Q^{\prime }_1\not \equiv 0$
(and in particular,
$Q^{\prime }_1\not \equiv 0$
(and in particular,
![]() $\alpha _1\neq 0$
), then either
$\alpha _1\neq 0$
), then either
![]() $a_1({\mathbf {z}})=b_1({\mathbf {z}})\equiv 0$
, in which case Equation (3.13) implies that
$a_1({\mathbf {z}})=b_1({\mathbf {z}})\equiv 0$
, in which case Equation (3.13) implies that
![]() $Q^{\prime }_1({\mathbf {z}})^2 =\alpha _1^2 A'({\mathbf {z}})B'({\mathbf {z}})$
, and we are done (as either both
$Q^{\prime }_1({\mathbf {z}})^2 =\alpha _1^2 A'({\mathbf {z}})B'({\mathbf {z}})$
, and we are done (as either both
![]() $A'$
and
$A'$
and
![]() $B'$
are squares or they are both multiples of
$B'$
are squares or they are both multiples of
![]() $Q^{\prime }_1$
), or equations (3.14) and (3.15) imply that
$Q^{\prime }_1$
), or equations (3.14) and (3.15) imply that
![]() $\alpha _1^2 A'({\mathbf {z}}) B'({\mathbf {z}}) = Q^{\prime }_1({\mathbf {z}})^2$
which again implies the claim.
$\alpha _1^2 A'({\mathbf {z}}) B'({\mathbf {z}}) = Q^{\prime }_1({\mathbf {z}})^2$
which again implies the claim.
This concludes the proof of Theorem 3.1 for the case
![]() $b\equiv 0$
and thus the proof of the theorem.
$b\equiv 0$
and thus the proof of the theorem.
4 Sylvester–Gallai theorem for quadratic polynomials
In this section, we prove Theorem 1.4. For convenience, we repeat the statement of the theorem.
Theorem 1.4. There exists a universal constant c such that the following holds. Let
![]() $\tilde {{\mathcal {Q}}} = \{Q_i\}_{i\in \{1,\ldots ,m\}}\subset \mathbb {C}[x_1,\ldots ,x_n]$
be a finite set of pairwise linearly independent homogeneous quadratic polynomials such that every
$\tilde {{\mathcal {Q}}} = \{Q_i\}_{i\in \{1,\ldots ,m\}}\subset \mathbb {C}[x_1,\ldots ,x_n]$
be a finite set of pairwise linearly independent homogeneous quadratic polynomials such that every
![]() $Q_i\in \tilde {{\mathcal {Q}}}$
is either irreducible or a square of a linear form. Assume that, for every
$Q_i\in \tilde {{\mathcal {Q}}}$
is either irreducible or a square of a linear form. Assume that, for every
![]() $i\neq j$
, whenever
$i\neq j$
, whenever
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
vanish, then so does
$Q_j$
vanish, then so does
![]() $\prod _{k\in \{1,\ldots ,m\} \setminus \{i,j\}} Q_k$
. Then,
$\prod _{k\in \{1,\ldots ,m\} \setminus \{i,j\}} Q_k$
. Then,
![]() $\dim (\operatorname {span}\{{{\mathcal {Q}}}\})\leq c$
.
$\dim (\operatorname {span}\{{{\mathcal {Q}}}\})\leq c$
.
Remark 4.1. The requirement that the polynomials are homogeneous is not essential as homogenization does not affect the property
![]() $Q_k\in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$
.
$Q_k\in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$
.
Remark 4.2. Note that we no longer demand that the polynomials are irreducible but rather allow some of them to be squares of linear forms, but now we restrict all polynomials to be of degree exactly
![]() $2$
. Note that both versions of the theorem are equivalent as this modification does not affect the vanishing condition.
$2$
. Note that both versions of the theorem are equivalent as this modification does not affect the vanishing condition.
Remark 4.3. Note that from Theorem 3.2 it follows that for every
![]() $i\neq j$
there exists a subset
$i\neq j$
there exists a subset
![]() ${\mathcal {K}} \subseteq [m]\setminus \{i,j\}$
such that
${\mathcal {K}} \subseteq [m]\setminus \{i,j\}$
such that
![]() $|{\mathcal {K}}|\leq 4$
, and whenever
$|{\mathcal {K}}|\leq 4$
, and whenever
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
vanish, then so does
$Q_j$
vanish, then so does
![]() $\prod _{k\in {\mathcal {K}}} Q_k$
.
$\prod _{k\in {\mathcal {K}}} Q_k$
.
In what follows, we shall use the following terminology. Whenever we say that two quadratics
![]() $Q_1,Q_2\in \tilde {\mathcal {Q}}$
satisfy Theorem 3.1(prime-case), we mean that there is a polynomial
$Q_1,Q_2\in \tilde {\mathcal {Q}}$
satisfy Theorem 3.1(prime-case), we mean that there is a polynomial
![]() $Q_3\in \tilde {\mathcal {Q}}\setminus \{Q_1,Q_2\}$
in their linear span. Similarly, when we say that they satisfy Theorem 3.1(product-case) (Theorem 3.1(linear-case)), we mean that there is a reducible quadratic in their linear span (they belong to
$Q_3\in \tilde {\mathcal {Q}}\setminus \{Q_1,Q_2\}$
in their linear span. Similarly, when we say that they satisfy Theorem 3.1(product-case) (Theorem 3.1(linear-case)), we mean that there is a reducible quadratic in their linear span (they belong to
![]() $\left \langle {a_1,a_2}\right \rangle $
for linear forms
$\left \langle {a_1,a_2}\right \rangle $
for linear forms
![]() $a_1,a_2$
).
$a_1,a_2$
).
Proof of Theorem 1.4.
Partition the polynomials to two sets. Let
![]() ${\mathcal {L}}$
be the set of all squares, and let
${\mathcal {L}}$
be the set of all squares, and let
![]() ${\mathcal {Q}}$
be the subset of irreducible quadratics, thus
${\mathcal {Q}}$
be the subset of irreducible quadratics, thus
![]() $\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$
. Denote
$\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$
. Denote
![]() $|{\mathcal {Q}}| = m$
,
$|{\mathcal {Q}}| = m$
,
![]() $|{\mathcal {L}}| = r$
. Let
$|{\mathcal {L}}| = r$
. Let
![]() $\delta =\frac {1}{100}$
, and denote
$\delta =\frac {1}{100}$
, and denote
-
•
 ${\mathcal {P}}_{\text {prime}} = \{P\in {\mathcal {Q}} \mid \text {There are at least } \delta m \text { polynomials in } {\mathcal {Q}} \text { such that } P \text { satisfies} \text {Theorem~3.1(prime-case) but not Theorem~3.1(product-case) with each of them} \}$
.
${\mathcal {P}}_{\text {prime}} = \{P\in {\mathcal {Q}} \mid \text {There are at least } \delta m \text { polynomials in } {\mathcal {Q}} \text { such that } P \text { satisfies} \text {Theorem~3.1(prime-case) but not Theorem~3.1(product-case) with each of them} \}$
. -
•
 ${\mathcal {P}}_{\text {linear}} = \{P\in {\mathcal {Q}} \mid \text {There are at least } \delta m \text { polynomials in } {\mathcal {Q}} \text { such that } P \text { satisfies} \text {Theorem~3.1(linear-case) with each of them} \}$
.
${\mathcal {P}}_{\text {linear}} = \{P\in {\mathcal {Q}} \mid \text {There are at least } \delta m \text { polynomials in } {\mathcal {Q}} \text { such that } P \text { satisfies} \text {Theorem~3.1(linear-case) with each of them} \}$
.
The proof first deals with the case where
![]() ${\mathcal {Q}} = {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
. We then handle the case that there is
${\mathcal {Q}} = {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
. We then handle the case that there is
![]() $Q \in {\mathcal {Q}} \setminus ({\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}})$
.
$Q \in {\mathcal {Q}} \setminus ({\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}})$
.
4.1 The case
 ${\mathcal {Q}}={\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
.
${\mathcal {Q}}={\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
.
Assume that
![]() ${\mathcal {Q}} = {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
. For our purposes, we may further assume that
${\mathcal {Q}} = {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
. For our purposes, we may further assume that
![]() ${\mathcal {P}}_{\text {prime}}\cap {\mathcal {P}}_{\text {linear}} = \emptyset $
by letting
${\mathcal {P}}_{\text {prime}}\cap {\mathcal {P}}_{\text {linear}} = \emptyset $
by letting
![]() ${\mathcal {P}}_{\text {prime}} = {\mathcal {P}}_{\text {prime}} \setminus {\mathcal {P}}_{\text {linear}}$
.
${\mathcal {P}}_{\text {prime}} = {\mathcal {P}}_{\text {prime}} \setminus {\mathcal {P}}_{\text {linear}}$
.
This is the simplest case in the analysis. The next claim shows that there is a small-dimensional linear space V such that
![]() ${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $
. The intuition is based on the following simple observation.
${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $
. The intuition is based on the following simple observation.
Observation 4.4. If
![]() $Q_1,Q_2 \in {\mathcal {Q}}$
satisfy Theorem 3.1(linear-case), then
$Q_1,Q_2 \in {\mathcal {Q}}$
satisfy Theorem 3.1(linear-case), then
![]() $\dim (\text {Lin}(Q_1)), \dim (\text {Lin}(Q_2)) \leq 4$
and
$\dim (\text {Lin}(Q_1)), \dim (\text {Lin}(Q_2)) \leq 4$
and
![]() $\dim (\text {Lin}(Q_1)\cap \text {Lin}(Q_2)) \geq 2$
.
$\dim (\text {Lin}(Q_1)\cap \text {Lin}(Q_2)) \geq 2$
.
The observation shows that if
![]() $Q \in {\mathcal {P}}_{\text {linear}}$
and we add to V a basis for
$Q \in {\mathcal {P}}_{\text {linear}}$
and we add to V a basis for
![]() $\text {Lin}(Q)$
, then any P that satisfies Theorem 3.1(linear-case) with Q now belongs to
$\text {Lin}(Q)$
, then any P that satisfies Theorem 3.1(linear-case) with Q now belongs to
![]() $\left \langle {V}\right \rangle $
. Choosing several such Q’s cleverly, we manage to cover all of
$\left \langle {V}\right \rangle $
. Choosing several such Q’s cleverly, we manage to cover all of
![]() ${\mathcal {P}}_{\text {linear}} $
.
${\mathcal {P}}_{\text {linear}} $
.
Claim 4.5. There exists a linear space of linear forms, V, such that
![]() $\dim (V)=O(1)$
and
$\dim (V)=O(1)$
and
![]() ${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $
.
${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $
.
Thus, we have many small-dimensional spaces that have large pairwise intersections, and we can therefore expect that such a V may exist.
Proof. We prove the existence of V by explicitly constructing it. Repeat the following process: Set
![]() $V = \{{\mathbf {0}}\}$
, and
$V = \{{\mathbf {0}}\}$
, and
![]() ${\mathcal {P}}'=\emptyset $
. At each step, consider any
${\mathcal {P}}'=\emptyset $
. At each step, consider any
![]() $Q \in {\mathcal {P}}_{\text {linear}}$
such that
$Q \in {\mathcal {P}}_{\text {linear}}$
such that
![]() $Q\notin \left \langle {V}\right \rangle $
, and set
$Q\notin \left \langle {V}\right \rangle $
, and set
![]() $V =\text {Lin}(Q) + V$
, and
$V =\text {Lin}(Q) + V$
, and
![]() ${\mathcal {P}}'={\mathcal {P}}' \cup \{Q\}$
. Repeat this process as long as possible, that is, as long as
${\mathcal {P}}'={\mathcal {P}}' \cup \{Q\}$
. Repeat this process as long as possible, that is, as long as
![]() ${\mathcal {P}}_{\text {linear}} \not \subseteq \left \langle {V}\right \rangle $
. We show next that this process must end after at most
${\mathcal {P}}_{\text {linear}} \not \subseteq \left \langle {V}\right \rangle $
. We show next that this process must end after at most
![]() $\frac {3}{\delta }$
steps. Namely,
$\frac {3}{\delta }$
steps. Namely,
![]() $|{\mathcal {P}}'| \leq \frac {3}{\delta }$
. It is clear that at the end of the process it holds that
$|{\mathcal {P}}'| \leq \frac {3}{\delta }$
. It is clear that at the end of the process it holds that
![]() ${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $
.
${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $
.
Let
![]() $Q\in {\mathcal {Q}}$
and
$Q\in {\mathcal {Q}}$
and
![]() ${\mathcal {B}}\subseteq {\mathcal {P}}'$
be the subset of all polynomials in
${\mathcal {B}}\subseteq {\mathcal {P}}'$
be the subset of all polynomials in
![]() ${\mathcal {P}}'$
that satisfy Theorem 3.1(linear-case) with Q. Observe that, if
${\mathcal {P}}'$
that satisfy Theorem 3.1(linear-case) with Q. Observe that, if
![]() $P_1,\ldots ,P_k$
are the first k elements of
$P_1,\ldots ,P_k$
are the first k elements of
![]() ${\mathcal {B}}$
that were added to
${\mathcal {B}}$
that were added to
![]() ${\mathcal {P}}'$
, then
${\mathcal {P}}'$
, then
![]() $Q,P_1,\ldots ,P_k$
satisfy the conditions of Theorem 2.23. In particular, this implies that
$Q,P_1,\ldots ,P_k$
satisfy the conditions of Theorem 2.23. In particular, this implies that
![]() $|{\mathcal {B}}| \leq 3$
.
$|{\mathcal {B}}| \leq 3$
.
For
![]() $Q_i \in {\mathcal {P}}'$
, define
$Q_i \in {\mathcal {P}}'$
, define
![]() $T_i =\{Q\in {\mathcal {Q}} \mid Q,Q_i \text { satisfy Theorem~3.1(linear-case)}\}$
. Since
$T_i =\{Q\in {\mathcal {Q}} \mid Q,Q_i \text { satisfy Theorem~3.1(linear-case)}\}$
. Since
![]() $|T_{i}|\geq \delta m$
and as by the discussion above each
$|T_{i}|\geq \delta m$
and as by the discussion above each
![]() $Q\in {\mathcal {Q}}$
belongs to at most
$Q\in {\mathcal {Q}}$
belongs to at most
![]() $3$
different sets, it follows by double counting that
$3$
different sets, it follows by double counting that
![]() $|{\mathcal {P}}'|\leq 3/\delta $
. As in each step we add at most
$|{\mathcal {P}}'|\leq 3/\delta $
. As in each step we add at most
![]() $4$
linearly independent linear forms to V, we obtain
$4$
linearly independent linear forms to V, we obtain
![]() $\dim (V)\leq \frac {12}{\delta }$
.
$\dim (V)\leq \frac {12}{\delta }$
.
This completes the proof of Theorem 4.5.
So far V satisfies that
![]() ${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $
. Next, we find a small set of polynomials
${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $
. Next, we find a small set of polynomials
![]() ${\mathcal {I}}$
such that
${\mathcal {I}}$
such that
![]() ${\mathcal {Q}} \subset \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}$
. The construction of
${\mathcal {Q}} \subset \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}$
. The construction of
![]() ${\mathcal {I}}$
is quite simple. Roughly, we iteratively add to
${\mathcal {I}}$
is quite simple. Roughly, we iteratively add to
![]() ${\mathcal {I}}$
any
${\mathcal {I}}$
any
![]() $P \in {\mathcal {P}}_{\text {prime}}\setminus \{ \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}\}$
. This is done in Theorem 4.6. We then show in Theorem 4.7 that each such polynomial P spans many other polynomials in
$P \in {\mathcal {P}}_{\text {prime}}\setminus \{ \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}\}$
. This is done in Theorem 4.6. We then show in Theorem 4.7 that each such polynomial P spans many other polynomials in
![]() $ {\mathcal {P}}_{\text {prime}}\setminus \{ \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}\}$
, and hence, this process terminates after a few steps. Interestingly, this may not cover all polynomials in
$ {\mathcal {P}}_{\text {prime}}\setminus \{ \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}\}$
, and hence, this process terminates after a few steps. Interestingly, this may not cover all polynomials in
![]() ${\mathcal {Q}}$
. We show however, that the remaining polynomials satisfy the conditions of the robust Sylvester–Gallai theorem and hence are contained themselves in a low-dimensional space. Theorem 4.8 is where we the complete proof.
${\mathcal {Q}}$
. We show however, that the remaining polynomials satisfy the conditions of the robust Sylvester–Gallai theorem and hence are contained themselves in a low-dimensional space. Theorem 4.8 is where we the complete proof.
Construction 4.6. Set
![]() ${\mathcal {I}}= \emptyset $
and
${\mathcal {I}}= \emptyset $
and
![]() ${\mathcal {B}}={\mathcal {P}}_{\text {linear}}$
. First, add to
${\mathcal {B}}={\mathcal {P}}_{\text {linear}}$
. First, add to
![]() ${\mathcal {B}}$
any polynomial from
${\mathcal {B}}$
any polynomial from
![]() ${\mathcal {P}}_{\text {prime}}$
that is in
${\mathcal {P}}_{\text {prime}}$
that is in
![]() $\left \langle {V}\right \rangle $
. Observe that at this point we have that
$\left \langle {V}\right \rangle $
. Observe that at this point we have that
![]() ${\mathcal {B}}\subset {\mathcal {Q}}\cap \left \langle {V}\right \rangle $
. Consider the following process: At each step, pick any
${\mathcal {B}}\subset {\mathcal {Q}}\cap \left \langle {V}\right \rangle $
. Consider the following process: At each step, pick any
![]() $P \in {\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$
such that P satisfies Theorem 3.1(prime-case), but not Theorem 3.1(product-case),Footnote
5
with at least
$P \in {\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$
such that P satisfies Theorem 3.1(prime-case), but not Theorem 3.1(product-case),Footnote
5
with at least
![]() $\frac {\delta }{3}m$
polynomials in
$\frac {\delta }{3}m$
polynomials in
![]() ${\mathcal {B}}$
, and add it to both
${\mathcal {B}}$
, and add it to both
![]() ${\mathcal {I}}$
and to
${\mathcal {I}}$
and to
![]() ${\mathcal {B}}$
. Then, we add to
${\mathcal {B}}$
. Then, we add to
![]() ${\mathcal {B}}$
all the polynomials
${\mathcal {B}}$
all the polynomials
![]() $P'\in {\mathcal {P}}_{\text {prime}}$
that satisfy
$P'\in {\mathcal {P}}_{\text {prime}}$
that satisfy
![]() $P' \in \operatorname {span}\{{({\mathcal {Q}} \cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$
. Note that we always maintain that
$P' \in \operatorname {span}\{{({\mathcal {Q}} \cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$
. Note that we always maintain that
![]() ${\mathcal {B}} \subset \operatorname {span}\{{({\mathcal {Q}} \cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$
. We continue this process as long as we can.
${\mathcal {B}} \subset \operatorname {span}\{{({\mathcal {Q}} \cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$
. We continue this process as long as we can.
Next, we prove that at the end of the process we have that
![]() $|{\mathcal {I}}| \leq 3/\delta $
.
$|{\mathcal {I}}| \leq 3/\delta $
.
Claim 4.7. In each step, we added to
![]() ${\mathcal {B}}$
at least
${\mathcal {B}}$
at least
![]() $\frac {\delta }{3}m$
new polynomials from
$\frac {\delta }{3}m$
new polynomials from
![]() ${\mathcal {P}}_{\text {prime}}$
. In particular,
${\mathcal {P}}_{\text {prime}}$
. In particular,
![]() $|{\mathcal {I}}| \leq 3/\delta $
.
$|{\mathcal {I}}| \leq 3/\delta $
.
Proof. Consider what happens when we add some polynomial P to
![]() ${\mathcal {I}}$
. By the description of our process, P satisfies Theorem 3.1(prime-case) with at least
${\mathcal {I}}$
. By the description of our process, P satisfies Theorem 3.1(prime-case) with at least
![]() $\frac {\delta }{3}m$
polynomials in
$\frac {\delta }{3}m$
polynomials in
![]() ${\mathcal {B}}$
. Any
${\mathcal {B}}$
. Any
![]() $Q\in {\mathcal {B}}$
that satisfies Theorem 3.1(prime-case) with P must span with P a polynomial
$Q\in {\mathcal {B}}$
that satisfies Theorem 3.1(prime-case) with P must span with P a polynomial
![]() $P'\in \tilde {{\mathcal {Q}}}$
. Observe that
$P'\in \tilde {{\mathcal {Q}}}$
. Observe that
![]() $P' \notin {\mathcal {L}}$
as
$P' \notin {\mathcal {L}}$
as
![]() $Q,P$
do not satisfy Theorem 3.1(product-case), and thus,
$Q,P$
do not satisfy Theorem 3.1(product-case), and thus,
![]() $P'\in {\mathcal {Q}}$
. It follows that
$P'\in {\mathcal {Q}}$
. It follows that
![]() $P'\in {\mathcal {P}}_{\text {prime}}$
since otherwise we would have that
$P'\in {\mathcal {P}}_{\text {prime}}$
since otherwise we would have that
![]() $P\in \operatorname {span}\{{{\mathcal {B}}}\}\subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$
, which implies
$P\in \operatorname {span}\{{{\mathcal {B}}}\}\subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$
, which implies
![]() $P\in {\mathcal {B}}$
in contradiction to the way that we defined the process. Furthermore, for each such
$P\in {\mathcal {B}}$
in contradiction to the way that we defined the process. Furthermore, for each such
![]() $Q\in {\mathcal {B}}$
the polynomial
$Q\in {\mathcal {B}}$
the polynomial
![]() $P'$
is unique. Indeed, if there was a
$P'$
is unique. Indeed, if there was a
![]() $P\neq P'\in {\mathcal {P}}_{\text {prime}}$
and
$P\neq P'\in {\mathcal {P}}_{\text {prime}}$
and
![]() $Q_1,Q_2\in {\mathcal {B}}$
such that
$Q_1,Q_2\in {\mathcal {B}}$
such that
![]() $P'\in \operatorname {span}\{{Q_1,P}\}\cap \operatorname {span}\{{Q_2,P}\}$
, then by pairwise independence we would conclude that
$P'\in \operatorname {span}\{{Q_1,P}\}\cap \operatorname {span}\{{Q_2,P}\}$
, then by pairwise independence we would conclude that
![]() $P\in \operatorname {span}\{{Q_1,Q_2}\}\subset \operatorname {span}\{{{\mathcal {B}}}\}$
, which, as we already showed, implies
$P\in \operatorname {span}\{{Q_1,Q_2}\}\subset \operatorname {span}\{{{\mathcal {B}}}\}$
, which, as we already showed, implies
![]() $P\in {\mathcal {B}}$
in contradiction. Thus, when we add P to
$P\in {\mathcal {B}}$
in contradiction. Thus, when we add P to
![]() ${\mathcal {I}}$
we add at least
${\mathcal {I}}$
we add at least
![]() $\frac {\delta }{3}m$
polynomials to
$\frac {\delta }{3}m$
polynomials to
![]() ${\mathcal {B}}$
. In particular, the process terminates after at most
${\mathcal {B}}$
. In particular, the process terminates after at most
![]() $3/\delta $
steps and thus
$3/\delta $
steps and thus
![]() $|{\mathcal {I}}|\leq 3/\delta $
.
$|{\mathcal {I}}|\leq 3/\delta $
.
We are now ready to complete the construction of
![]() ${\mathcal {I}}$
.
${\mathcal {I}}$
.
Claim 4.8. There exists a set
![]() ${\mathcal {I}}\subset {\mathcal {Q}}$
such that
${\mathcal {I}}\subset {\mathcal {Q}}$
such that
![]() ${\mathcal {Q}} \subset \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}$
and
${\mathcal {Q}} \subset \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}$
and
![]() $|{\mathcal {I}}|= O(1/\delta ) $
.
$|{\mathcal {I}}|= O(1/\delta ) $
.
Proof. Let
![]() ${\mathcal {I}}$
and
${\mathcal {I}}$
and
![]() ${\mathcal {B}}$
be as above. Consider the polynomials left in
${\mathcal {B}}$
be as above. Consider the polynomials left in
![]() ${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$
. As they ‘survived’ the process, each of them satisfies the condition in the definition of
${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$
. As they ‘survived’ the process, each of them satisfies the condition in the definition of
![]() ${\mathcal {P}}_{\text {prime}}$
with at most
${\mathcal {P}}_{\text {prime}}$
with at most
![]() $\frac {\delta }{3}m$
polynomials in
$\frac {\delta }{3}m$
polynomials in
![]() ${\mathcal {B}}$
. From the fact that
${\mathcal {B}}$
. From the fact that
![]() ${\mathcal {P}}_{\text {linear}}\subseteq {\mathcal {B}}$
and the uniqueness property we obtained in the proof of Theorem 4.7, we get that
${\mathcal {P}}_{\text {linear}}\subseteq {\mathcal {B}}$
and the uniqueness property we obtained in the proof of Theorem 4.7, we get that
![]() ${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$
satisfies the conditions of Theorem 2.6 with parameter
${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$
satisfies the conditions of Theorem 2.6 with parameter
![]() $\delta /3$
, and thus, Theorem 2.7 implies that
$\delta /3$
, and thus, Theorem 2.7 implies that
![]() $\dim ({\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}})\leq O(1/\delta )$
. Adding a basis of
$\dim ({\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}})\leq O(1/\delta )$
. Adding a basis of
![]() ${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$
to
${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$
to
![]() ${\mathcal {I}}$
, we get that
${\mathcal {I}}$
, we get that
![]() $|{\mathcal {I}}| = O(1/\delta )$
and every polynomial in
$|{\mathcal {I}}| = O(1/\delta )$
and every polynomial in
![]() ${\mathcal {Q}}$
is in
${\mathcal {Q}}$
is in
![]() $\operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$
.
$\operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$
.
We are not done yet as the dimension of
![]() $\left \langle {V}\right \rangle $
, as a vector space, is not a constant. Nevertheless, we next show how to use Theorem 2.10 to bound the dimension of
$\left \langle {V}\right \rangle $
, as a vector space, is not a constant. Nevertheless, we next show how to use Theorem 2.10 to bound the dimension of
![]() ${\mathcal {Q}}$
, given that
${\mathcal {Q}}$
, given that
![]() ${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$
. To achieve this, we introduce yet another iterative process: For each
${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$
. To achieve this, we introduce yet another iterative process: For each
![]() $P\in {\mathcal {Q}}\setminus \left \langle {V}\right \rangle $
, if there is quadratic L, with
$P\in {\mathcal {Q}}\setminus \left \langle {V}\right \rangle $
, if there is quadratic L, with
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(L) \leq 2$
, such that
$\operatorname {\mathrm {rank}}_{\text {s}}(L) \leq 2$
, such that
![]() $P + L \in \left \langle {V}\right \rangle $
, then we set
$P + L \in \left \langle {V}\right \rangle $
, then we set
![]() $V = V+\text {Lin}(L)$
(this increases the dimension of V by at most
$V = V+\text {Lin}(L)$
(this increases the dimension of V by at most
![]() $4$
). Since this operation increases
$4$
). Since this operation increases
![]() $\dim \left ( \left \langle {V}\right \rangle \cap {\mathcal {Q}} \right )$
, we can remove one polynomial from
$\dim \left ( \left \langle {V}\right \rangle \cap {\mathcal {Q}} \right )$
, we can remove one polynomial from
![]() ${\mathcal {I}}$
, and thus decrease its size by
${\mathcal {I}}$
, and thus decrease its size by
![]() $1$
, and still maintain the property that
$1$
, and still maintain the property that
![]() ${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$
. We repeat this process until either
${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$
. We repeat this process until either
![]() ${\mathcal {I}}$
is empty, or none of the polynomials in
${\mathcal {I}}$
is empty, or none of the polynomials in
![]() ${\mathcal {I}}$
satisfy the condition of the process. By the upper bound on
${\mathcal {I}}$
satisfy the condition of the process. By the upper bound on
![]() $|{\mathcal {I}}|$
, the dimension of V grew by at most
$|{\mathcal {I}}|$
, the dimension of V grew by at most
![]() $4|{\mathcal {I}}|= O( 1/{\delta })$
, and thus, it remains of dimension
$4|{\mathcal {I}}|= O( 1/{\delta })$
, and thus, it remains of dimension
![]() $O( 1/{\delta })=O(1)$
. At the end of the process, we have that
$O( 1/{\delta })=O(1)$
. At the end of the process, we have that
![]() ${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$
and that every polynomial in
${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$
and that every polynomial in
![]() $P \in {\mathcal {Q}}\setminus \left \langle {V}\right \rangle $
has
$P \in {\mathcal {Q}}\setminus \left \langle {V}\right \rangle $
has
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(P)> 2$
, even if we set all linear forms in V to zero.
$\operatorname {\mathrm {rank}}_{\text {s}}(P)> 2$
, even if we set all linear forms in V to zero.
Consider the map
![]() $T_{{\boldsymbol {\alpha }},V}$
as given in Theorem 2.24, for a randomly chosen
$T_{{\boldsymbol {\alpha }},V}$
as given in Theorem 2.24, for a randomly chosen
![]() ${\boldsymbol {\alpha }}\in [0,1]^{\dim (V)}$
. Each polynomial in
${\boldsymbol {\alpha }}\in [0,1]^{\dim (V)}$
. Each polynomial in
![]() ${\mathcal {Q}}\cap \left \langle {V}\right \rangle $
is mapped to a polynomial of the form
${\mathcal {Q}}\cap \left \langle {V}\right \rangle $
is mapped to a polynomial of the form
![]() $zb$
, for some linear form b. From Theorem 2.16, it follows that every polynomial in
$zb$
, for some linear form b. From Theorem 2.16, it follows that every polynomial in
![]() ${\mathcal {Q}}\setminus \left \langle {V}\right \rangle $
still has rank larger than
${\mathcal {Q}}\setminus \left \langle {V}\right \rangle $
still has rank larger than
![]() $2$
after the mapping. Let
$2$
after the mapping. Let
We now show that, modulo z,
![]() ${\mathcal {A}}$
satisfies the conditions of Theorem 2.10. Let
${\mathcal {A}}$
satisfies the conditions of Theorem 2.10. Let
![]() $b_1,b_2\in {\mathcal {A}}$
such that
$b_1,b_2\in {\mathcal {A}}$
such that
![]() $b_1 \not \in \operatorname {span}\{{z}\}$
and
$b_1 \not \in \operatorname {span}\{{z}\}$
and
![]() $b_2 \not \in \operatorname {span}\{{z,b_1}\}$
. As
$b_2 \not \in \operatorname {span}\{{z,b_1}\}$
. As
![]() $\tilde {\mathcal {Q}}$
satisfies the conditions of Theorem 1.4, we get that there are polynomials
$\tilde {\mathcal {Q}}$
satisfies the conditions of Theorem 1.4, we get that there are polynomials
![]() $Q_1,\ldots ,Q_4 \in \tilde {\mathcal {Q}}$
such that
$Q_1,\ldots ,Q_4 \in \tilde {\mathcal {Q}}$
such that
![]() $\prod _{i=1}^{4}T_{{\boldsymbol {\alpha }},V}(Q_i) \in \sqrt {\left \langle {b_1,b_2}\right \rangle }=\left \langle {b_1,b_2}\right \rangle $
, where the equality holds as
$\prod _{i=1}^{4}T_{{\boldsymbol {\alpha }},V}(Q_i) \in \sqrt {\left \langle {b_1,b_2}\right \rangle }=\left \langle {b_1,b_2}\right \rangle $
, where the equality holds as
![]() $\left \langle {b_1,b_2}\right \rangle $
is a prime ideal. This fact also implies that, without loss of generality,
$\left \langle {b_1,b_2}\right \rangle $
is a prime ideal. This fact also implies that, without loss of generality,
![]() $T_{{\boldsymbol {\alpha }},V}(Q_4)\in \left \langle {b_1,b_2}\right \rangle $
. Thus,
$T_{{\boldsymbol {\alpha }},V}(Q_4)\in \left \langle {b_1,b_2}\right \rangle $
. Thus,
![]() $T_{{\boldsymbol {\alpha }},V}(Q_4)$
has rank at most
$T_{{\boldsymbol {\alpha }},V}(Q_4)$
has rank at most
![]() $2$
and therefore
$2$
and therefore
![]() $Q_4\in {\mathcal {L}}\cup ({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) $
. Hence,
$Q_4\in {\mathcal {L}}\cup ({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) $
. Hence,
![]() $T_{{\boldsymbol {\alpha }},V}(Q_4)$
was mapped to
$T_{{\boldsymbol {\alpha }},V}(Q_4)$
was mapped to
![]() $zb_4$
or to
$zb_4$
or to
![]() $b_4^2$
. In particular,
$b_4^2$
. In particular,
![]() $b_4\in {\mathcal {A}}$
. Theorem 2.26 and Theorem 2.27 imply that
$b_4\in {\mathcal {A}}$
. Theorem 2.26 and Theorem 2.27 imply that
![]() $b_4$
is neither a multiple of
$b_4$
is neither a multiple of
![]() $b_1$
nor a multiple of
$b_1$
nor a multiple of
![]() $b_2$
, so it must hold that
$b_2$
, so it must hold that
![]() $b_4$
depends nontrivially on both
$b_4$
depends nontrivially on both
![]() $b_1$
and
$b_1$
and
![]() $b_2$
. Thus,
$b_2$
. Thus,
![]() ${\mathcal {A}}$
satisfies the conditions of Theorem 2.10 modulo z. It follows that
${\mathcal {A}}$
satisfies the conditions of Theorem 2.10 modulo z. It follows that
![]() $\dim ({\mathcal {A}})\leq 4$
.
$\dim ({\mathcal {A}})\leq 4$
.
The argument above shows that the dimension of
![]() $T_{{\boldsymbol {\alpha }},V}({\mathcal {L}}\cup ({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) ) =O(1)$
. Theorem 2.29 implies that if we denote
$T_{{\boldsymbol {\alpha }},V}({\mathcal {L}}\cup ({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) ) =O(1)$
. Theorem 2.29 implies that if we denote
![]() $U = \operatorname {span}\{{{\mathcal {L}} \cup \text {Lin}({\mathcal {Q}}\cap \left \langle {V}\right \rangle )}\}$
then
$U = \operatorname {span}\{{{\mathcal {L}} \cup \text {Lin}({\mathcal {Q}}\cap \left \langle {V}\right \rangle )}\}$
then
![]() $\dim (U )$
is
$\dim (U )$
is
![]() $(4+1)\cdot \dim (V)=O(1/\delta )$
. As
$(4+1)\cdot \dim (V)=O(1/\delta )$
. As
![]() ${\mathcal {Q}} \subseteq \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$
, we obtain that
${\mathcal {Q}} \subseteq \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$
, we obtain that
![]() $\dim (\tilde {\mathcal {Q}})=\dim ({\mathcal {L}}\cup {\mathcal {Q}}) = O(1/\delta )=O(1)$
, as we wanted to show.
$\dim (\tilde {\mathcal {Q}})=\dim ({\mathcal {L}}\cup {\mathcal {Q}}) = O(1/\delta )=O(1)$
, as we wanted to show.
This completes the proof of Theorem 1.4 for the case
![]() ${\mathcal {Q}}={\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
.
${\mathcal {Q}}={\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
.
4.2 The case
 ${\mathcal {Q}}\neq {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
.
${\mathcal {Q}}\neq {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
.
In this case, there is some polynomial
![]() $Q_o \in {\mathcal {Q}} \setminus ({{\mathcal {P}}}_1\cup {{\mathcal {P}}}_3)$
. In particular,
$Q_o \in {\mathcal {Q}} \setminus ({{\mathcal {P}}}_1\cup {{\mathcal {P}}}_3)$
. In particular,
![]() $Q_o$
satisfies Theorem 3.1(product-case) with at least
$Q_o$
satisfies Theorem 3.1(product-case) with at least
![]() $(1-2\delta )m$
of the polynomials in
$(1-2\delta )m$
of the polynomials in
![]() ${\mathcal {Q}}$
; of the remaining polynomials, at most
${\mathcal {Q}}$
; of the remaining polynomials, at most
![]() $\delta m$
satisfy Theorem 3.1(prime-case) with
$\delta m$
satisfy Theorem 3.1(prime-case) with
![]() $Q_o$
; similarly, at most
$Q_o$
; similarly, at most
![]() $\delta m$
polynomials satisfy Theorem 3.1(linear-case) with
$\delta m$
polynomials satisfy Theorem 3.1(linear-case) with
![]() $Q_o$
. Let
$Q_o$
. Let
-
•
 ${\mathcal {Q}}_{\text {prod}} = \{P \in {\mathcal {Q}} \mid P,Q_o \text { satisfy Theorem}~{3.1}\text{(product-case) }\} \cup \{Q_o\}$
${\mathcal {Q}}_{\text {prod}} = \{P \in {\mathcal {Q}} \mid P,Q_o \text { satisfy Theorem}~{3.1}\text{(product-case) }\} \cup \{Q_o\}$
-
•
 ${\mathcal {Q}}_{\neg \text {prod}} = \{P \in {\mathcal {Q}} \mid P,Q_o \text { do not satisfy Theorem}~{3.1}\text{(product-case)}\}$
${\mathcal {Q}}_{\neg \text {prod}} = \{P \in {\mathcal {Q}} \mid P,Q_o \text { do not satisfy Theorem}~{3.1}\text{(product-case)}\}$
-
•
 $m_1+1 = |{\mathcal {Q}}_{\text {prod}}|$
,
$m_1+1 = |{\mathcal {Q}}_{\text {prod}}|$
,
 $m_2 = |{\mathcal {Q}}_{\neg \text {prod}}|$
.
$m_2 = |{\mathcal {Q}}_{\neg \text {prod}}|$
.
As
![]() $Q_o \notin {\mathcal {P}}_{\text {prime}} \cup {\mathcal {P}}_{\text {linear}}$
, we have that
$Q_o \notin {\mathcal {P}}_{\text {prime}} \cup {\mathcal {P}}_{\text {linear}}$
, we have that
![]() $m_2 \leq 2\delta m$
and
$m_2 \leq 2\delta m$
and
![]() $m_1 \geq (1-2\delta )m$
. These properties of
$m_1 \geq (1-2\delta )m$
. These properties of
![]() $Q_o$
and
$Q_o$
and
![]() ${\mathcal {Q}}$
are captured by the following definition.
${\mathcal {Q}}$
are captured by the following definition.
Definition 4.9. Let
![]() ${\mathcal {Q}}_{\text {prod}} = \{Q_o,Q_1,\ldots ,Q_{m_1}\hspace{-0.5pt}\}$
and
${\mathcal {Q}}_{\text {prod}} = \{Q_o,Q_1,\ldots ,Q_{m_1}\hspace{-0.5pt}\}$
and
![]() ${\mathcal {Q}}_{\neg \text {prod}} = \{{P}_1,\ldots , {P}_{m_2}\}$
be sets of irreducible homogeneous quadratic polynomials. Let
${\mathcal {Q}}_{\neg \text {prod}} = \{{P}_1,\ldots , {P}_{m_2}\}$
be sets of irreducible homogeneous quadratic polynomials. Let
![]() ${\mathcal {L}} = \{a_{m_1+1}^2,\ldots ,a_{m_1+r}^2\}$
be a set of squares of homogeneous linear forms. We say that
${\mathcal {L}} = \{a_{m_1+1}^2,\ldots ,a_{m_1+r}^2\}$
be a set of squares of homogeneous linear forms. We say that
![]() $\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$
, where
$\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$
, where
![]() ${\mathcal {Q}}={\mathcal {Q}}_{\text {prod}}\cup {\mathcal {Q}}_{\neg \text {prod}}$
is a
${\mathcal {Q}}={\mathcal {Q}}_{\text {prod}}\cup {\mathcal {Q}}_{\neg \text {prod}}$
is a
![]() $(Q_o,m_1,m_2)$
-set if it satisfies the following:
$(Q_o,m_1,m_2)$
-set if it satisfies the following:
-
1.
 $\tilde {{\mathcal {Q}}}$
satisfy the conditions in the statement of Theorem 1.4.
$\tilde {{\mathcal {Q}}}$
satisfy the conditions in the statement of Theorem 1.4. -
2.
 $m_1> 5m_2+2$
.
$m_1> 5m_2+2$
. -
3. For every
 $j\in [m_1]$
, there are linear forms
$j\in [m_1]$
, there are linear forms
 $a_j,b_j$
such that
$a_j,b_j$
such that
 $Q_j = Q_o + a_j b_j$
.
$Q_j = Q_o + a_j b_j$
. -
4. For every
 $i\in [m_2]$
, every nontrivial linear combination of
$i\in [m_2]$
, every nontrivial linear combination of
 $P_i$
and
$P_i$
and
 $Q_o$
has rank at least
$Q_o$
has rank at least
 $2$
.
$2$
. -
5. At most
 $m_2$
of the polynomials in
$m_2$
of the polynomials in
 ${\mathcal {Q}}$
satisfy Theorem 3.1(linear-case) with
${\mathcal {Q}}$
satisfy Theorem 3.1(linear-case) with
 $Q_o$
.
$Q_o$
.
By the discussion above, the following theorem is what we need in order to complete the proof for the case
![]() ${\mathcal {Q}}\neq {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
.
${\mathcal {Q}}\neq {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$
.
Theorem 4.10. Let
![]() $\tilde {{\mathcal {Q}}}$
satisfy the conditions of Theorem 4.9, then
$\tilde {{\mathcal {Q}}}$
satisfy the conditions of Theorem 4.9, then
![]() $\dim {\tilde {{\mathcal {Q}}}} = O(1)$
.
$\dim {\tilde {{\mathcal {Q}}}} = O(1)$
.
We prove this theorem in section 5 to conclude the proof of Theorem 2.11.
![]() $\Box $
$\Box $
5 Proof of Theorem 4.10
Using the notation of Theorem 4.9, we denote, for
![]() $Q_i=Q_o+a_ib_i\in {\mathcal {Q}}_{\text {prod}}$
,
$Q_i=Q_o+a_ib_i\in {\mathcal {Q}}_{\text {prod}}$
,
![]() $V_i := \operatorname {span}\{{a_i,b_i}\}$
, and for
$V_i := \operatorname {span}\{{a_i,b_i}\}$
, and for
![]() $Q_k=a_k^2 \in {\mathcal {L}}$
, we let
$Q_k=a_k^2 \in {\mathcal {L}}$
, we let
![]() $V_i=\operatorname {span}\{{a_k}\}$
.Footnote
6
$V_i=\operatorname {span}\{{a_k}\}$
.Footnote
6
The main idea is (roughly) proving that
![]() ${\mathcal {L}}\cup \bigcup V_i$
satisfies the conditions of the Sylvester–Gallai theorem (or its robust version). To this end, we first show, in subsection 5.1, that the different spaces
${\mathcal {L}}\cup \bigcup V_i$
satisfies the conditions of the Sylvester–Gallai theorem (or its robust version). To this end, we first show, in subsection 5.1, that the different spaces
![]() $V_i$
satisfy some nontrivial intersection properties (Theorem 5.2). We then show in subsection 5.2 that there is a small-dimensional V that contains ‘most’ of the
$V_i$
satisfy some nontrivial intersection properties (Theorem 5.2). We then show in subsection 5.2 that there is a small-dimensional V that contains ‘most’ of the
![]() $\{a_i,b_i\}$
when
$\{a_i,b_i\}$
when
![]() ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
(Theorem 5.4). Then in subsection 5.3, we prove that there exists a constant-dimensional linear space of linear forms V (if
${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
(Theorem 5.4). Then in subsection 5.3, we prove that there exists a constant-dimensional linear space of linear forms V (if
![]() ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
, then this is the V that we found in subsection 5.2) such that, for some
${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
, then this is the V that we found in subsection 5.2) such that, for some
![]() $\alpha \in \{0,1\}$
, every polynomial
$\alpha \in \{0,1\}$
, every polynomial
![]() $F\in \tilde {{\mathcal {Q}}}$
(more or less) has the form
$F\in \tilde {{\mathcal {Q}}}$
(more or less) has the form
![]() $F = \alpha Q_o +F' + c(\varepsilon c + v )$
, where c is a linear form,
$F = \alpha Q_o +F' + c(\varepsilon c + v )$
, where c is a linear form,
![]() $\varepsilon \in \mathbb {C}$
,
$\varepsilon \in \mathbb {C}$
,
![]() $v\in V$
and
$v\in V$
and
![]() $F'\in \mathbb {C}[V]$
(Theorem 5.6). This structure is already very close to the claim of Theorem 4.10, and we conclude the proof in subsection 5.4 by showing that the different linear functions c satisfy the robust Sylvester–Gallai theorem (Claims 5.7 and 5.9). One case that we omitted from the description above is that, when the rank of
$F'\in \mathbb {C}[V]$
(Theorem 5.6). This structure is already very close to the claim of Theorem 4.10, and we conclude the proof in subsection 5.4 by showing that the different linear functions c satisfy the robust Sylvester–Gallai theorem (Claims 5.7 and 5.9). One case that we omitted from the description above is that, when the rank of
![]() $Q_o$
is small, We can also have
$Q_o$
is small, We can also have
![]() $F\in \left \langle {V}\right \rangle $
. In the proof of Theorem 5.9, we handle this case using projection mappings (recall subsection 2.5).
$F\in \left \langle {V}\right \rangle $
. In the proof of Theorem 5.9, we handle this case using projection mappings (recall subsection 2.5).
5.1 Intersection properties of the
 $V_i$
s
$V_i$
s
We start by proving that the spaces
![]() $V_i$
s that were defined above intersect nontrivially under some mild condition. The proof follows almost immediately from Theorem 3.1.
$V_i$
s that were defined above intersect nontrivially under some mild condition. The proof follows almost immediately from Theorem 3.1.
Claim 5.1. Let
![]() $\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$
be a
$\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$
be a
![]() $(Q_o,m_1,m_2)\text{-}{set}$
, and let
$(Q_o,m_1,m_2)\text{-}{set}$
, and let
![]() $Q_i=Q_o+a_ib_i$
and
$Q_i=Q_o+a_ib_i$
and
![]() $Q_j= Q_o+a_jb_j$
be polynomials in
$Q_j= Q_o+a_jb_j$
be polynomials in
![]() ${\mathcal {Q}}_{\text {prod}}$
such that for every
${\mathcal {Q}}_{\text {prod}}$
such that for every
![]() $\alpha \neq 0$
,
$\alpha \neq 0$
,
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$
.
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$
.
-
1. If there exists
 $k\in [m_1+r]\setminus \{i,j\}$
such that
$k\in [m_1+r]\setminus \{i,j\}$
such that
 $Q_k\in \operatorname {span}\{{Q_i,Q_j}\}$
, then, for some
$Q_k\in \operatorname {span}\{{Q_i,Q_j}\}$
, then, for some
 $\alpha ,\beta \in \mathbb {C}\setminus \{0\}$
(5.1)
$\alpha ,\beta \in \mathbb {C}\setminus \{0\}$
(5.1) $$ \begin{align} \alpha a_ib_i + \beta a_jb_j = a_k b_k. \end{align} $$
$$ \begin{align} \alpha a_ib_i + \beta a_jb_j = a_k b_k. \end{align} $$
-
2. If
 $Q_i$
and
$Q_i$
and
 $Q_j$
satisfy Theorem 3.1(product-case), then there exist two linear forms c and d such that (5.2)
$Q_j$
satisfy Theorem 3.1(product-case), then there exist two linear forms c and d such that (5.2) $$ \begin{align} a_ib_i - a_jb_j = cd. \end{align} $$
$$ \begin{align} a_ib_i - a_jb_j = cd. \end{align} $$
-
3.
 $Q_i$
and
$Q_i$
and
 $Q_j$
do not satisfy Theorem 3.1(linear-case).
$Q_j$
do not satisfy Theorem 3.1(linear-case).
Note that the guarantee of this claim is not sufficient to conclude that the dimension of
![]() ${a}_1,\ldots , {a}_{m_1}, {b}_1,\ldots , {b}_{m_1}$
is bounded. The reason is that c and d are not necessarily in the union of
${a}_1,\ldots , {a}_{m_1}, {b}_1,\ldots , {b}_{m_1}$
is bounded. The reason is that c and d are not necessarily in the union of
![]() $V_i$
s (or in
$V_i$
s (or in
![]() ${\mathcal {L}}$
). For example, if for every i,
${\mathcal {L}}$
). For example, if for every i,
![]() $a_ib_i = x_i^2 - x_1^2$
, then every pair,
$a_ib_i = x_i^2 - x_1^2$
, then every pair,
![]() $Q_i, Q_j$
satisfies Theorem 3.1(product-case), but the dimension of
$Q_i, Q_j$
satisfies Theorem 3.1(product-case), but the dimension of
![]() $\{{a}_1,\ldots , {a}_{m_1}, {b}_1,\ldots , {b}_{m_1}\}$
is unbounded.
$\{{a}_1,\ldots , {a}_{m_1}, {b}_1,\ldots , {b}_{m_1}\}$
is unbounded.
Proof of Theorem 5.1.
If, for
![]() $k \in [m_1+r]\setminus \{i,j\}$
,
$k \in [m_1+r]\setminus \{i,j\}$
,
![]() $Q_k\in \operatorname {span}\{{Q_i,Q_j}\}$
, then there are constants
$Q_k\in \operatorname {span}\{{Q_i,Q_j}\}$
, then there are constants
![]() $\alpha , \beta \in \mathbb {C}$
such that
$\alpha , \beta \in \mathbb {C}$
such that
![]() $\alpha (Q_o+a_ib_i) + \beta ( Q_o+a_jb_j) = \alpha Q_i+\beta Q_j = Q_k = \alpha _k Q_o+a_kb_k$
.Footnote
7
Rearranging, we get that
$\alpha (Q_o+a_ib_i) + \beta ( Q_o+a_jb_j) = \alpha Q_i+\beta Q_j = Q_k = \alpha _k Q_o+a_kb_k$
.Footnote
7
Rearranging, we get that
As
![]() $\alpha \neq 0$
(since
$\alpha \neq 0$
(since
![]() $Q_j \not \sim Q_k$
),
$Q_j \not \sim Q_k$
),
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$
, which implies that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$
, which implies that
![]() $\alpha _k-(\alpha +\beta ) = 0$
. Hence,
$\alpha _k-(\alpha +\beta ) = 0$
. Hence,
and equation (5.1) holds. As before,
![]() $\alpha , \beta \neq 0$
since otherwise we will have two linearly dependent polynomials in
$\alpha , \beta \neq 0$
since otherwise we will have two linearly dependent polynomials in
![]() ${\mathcal {Q}}$
.
${\mathcal {Q}}$
.
If
![]() $Q_i,Q_j$
satisfy Theorem 3.1(product-case), then there are
$Q_i,Q_j$
satisfy Theorem 3.1(product-case), then there are
![]() $\alpha , \beta \in \mathbb {C}$
and two linear forms c and d such that
$\alpha , \beta \in \mathbb {C}$
and two linear forms c and d such that
![]() $ \alpha (Q_o+a_ib_i) + \beta ( Q_o+a_jb_j) = cd$
, and again, by the same argument, we get that
$ \alpha (Q_o+a_ib_i) + \beta ( Q_o+a_jb_j) = cd$
, and again, by the same argument, we get that
![]() $\beta = -\alpha $
, and that, without loss of generality,
$\beta = -\alpha $
, and that, without loss of generality,
As
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_i)\geq 3$
they cannot satisfy Theorem 3.1(linear-case).
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_i)\geq 3$
they cannot satisfy Theorem 3.1(linear-case).
Corollary 5.2. Let
![]() $\tilde {{\mathcal {Q}}}$
be a
$\tilde {{\mathcal {Q}}}$
be a
![]() $(Q_o,m_1,m_2)\text{-}{set}$
. If for some
$(Q_o,m_1,m_2)\text{-}{set}$
. If for some
![]() $i\in [m_1]$
we have that
$i\in [m_1]$
we have that
![]() $\dim (V_i)=2$
and
$\dim (V_i)=2$
and
![]() $Q_i$
satisfies that for every
$Q_i$
satisfies that for every
![]() $\alpha \neq 0$
,
$\alpha \neq 0$
,
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$
, then for every
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$
, then for every
![]() $j \in [m_1]$
it holds that
$j \in [m_1]$
it holds that
![]() $\dim (V_j\cap V_i) \geq 1$
. In particular, it follows that, if
$\dim (V_j\cap V_i) \geq 1$
. In particular, it follows that, if
![]() $dim(V_j)=1$
, then
$dim(V_j)=1$
, then
![]() $V_j\varsubsetneq V_i$
.
$V_j\varsubsetneq V_i$
.
5.2 Constructing V using
 ${\mathcal {Q}}_{\neg \text {prod}}$
${\mathcal {Q}}_{\neg \text {prod}}$
In this section, we show that, if
![]() ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
, then we can use any polynomial in it to define a linear space of linear forms V that contains many of the
${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
, then we can use any polynomial in it to define a linear space of linear forms V that contains many of the
![]() $V_i$
s. We first prove a simple claim showing that every polynomial in
$V_i$
s. We first prove a simple claim showing that every polynomial in
![]() ${\mathcal {Q}_{\neg \text {prod}}}$
is a linear combination of
${\mathcal {Q}_{\neg \text {prod}}}$
is a linear combination of
![]() $Q_o$
and a quadratic polynomial of rank
$Q_o$
and a quadratic polynomial of rank
![]() $2$
.
$2$
.
Claim 5.3. Let
![]() $\tilde {{\mathcal {Q}}}$
be a
$\tilde {{\mathcal {Q}}}$
be a
![]() $(Q_o,m_1,m_2)\text{-}{set}$
. Then for every
$(Q_o,m_1,m_2)\text{-}{set}$
. Then for every
![]() $i\in [m_2]$
, there exists
$i\in [m_2]$
, there exists
![]() $ \gamma _i\in \mathbb {C}$
such that
$ \gamma _i\in \mathbb {C}$
such that
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(P_i-\gamma _i Q_o) = 2$
.
$\operatorname {\mathrm {rank}}_{\text {s}}(P_i-\gamma _i Q_o) = 2$
.
Proof. Consider any
![]() $P_i$
for
$P_i$
for
![]() $i\in [m_2]$
. We shall analyze, for each
$i\in [m_2]$
. We shall analyze, for each
![]() $j \in [m_1]$
, which case of Theorem 3.1
$j \in [m_1]$
, which case of Theorem 3.1
![]() $Q_j$
and
$Q_j$
and
![]() $P_i$
satisfy.
$P_i$
satisfy.
If
![]() $P_i$
satisfies Theorem 3.1(linear-case) with any
$P_i$
satisfies Theorem 3.1(linear-case) with any
![]() $Q_j\in {\mathcal {Q}}_{\text {prod}}$
, then the claim holds with
$Q_j\in {\mathcal {Q}}_{\text {prod}}$
, then the claim holds with
![]() $\gamma _i=0$
. If
$\gamma _i=0$
. If
![]() $P_i$
satisfies Theorem 3.1(product-case) with any
$P_i$
satisfies Theorem 3.1(product-case) with any
![]() $Q_j\in {\mathcal {Q}}$
, then there exist linear forms c and d and nonzero
$Q_j\in {\mathcal {Q}}$
, then there exist linear forms c and d and nonzero
![]() $\alpha , \beta \in \mathbb {C}$
such that
$\alpha , \beta \in \mathbb {C}$
such that
 $$ \begin{align} P_i = \frac{1}{\alpha}\left(cd - \beta \left(Q_o+a_j b_j\right)\right) = \frac{-\beta}{\alpha}Q_o + \left(\frac{1}{\alpha} cd - \frac{\beta}{\alpha} a_j b_j\right) . \end{align} $$
$$ \begin{align} P_i = \frac{1}{\alpha}\left(cd - \beta \left(Q_o+a_j b_j\right)\right) = \frac{-\beta}{\alpha}Q_o + \left(\frac{1}{\alpha} cd - \frac{\beta}{\alpha} a_j b_j\right) . \end{align} $$
Observe that the rank of
![]() $cd - \beta a_j b_j$
cannot be
$cd - \beta a_j b_j$
cannot be
![]() $1$
by Theorem 4.9. Hence, the statement holds with
$1$
by Theorem 4.9. Hence, the statement holds with
![]() $\gamma _i = -\frac {\beta }{\alpha }$
.
$\gamma _i = -\frac {\beta }{\alpha }$
.
Thus, the only case left to consider is when
![]() $P_i$
satisfies Theorem 3.1(prime-case) with all the
$P_i$
satisfies Theorem 3.1(prime-case) with all the
![]() $Q_j$
’s in
$Q_j$
’s in
![]() ${\mathcal {Q}}_{\text {prod}}$
. We next show that in this case there must exist
${\mathcal {Q}}_{\text {prod}}$
. We next show that in this case there must exist
![]() $j\neq j' \in [m_1]$
such that
$j\neq j' \in [m_1]$
such that
![]() $Q_{j'}\in \operatorname {span}\{{Q_j,P_i}\}$
. Observe that this would imply that there are
$Q_{j'}\in \operatorname {span}\{{Q_j,P_i}\}$
. Observe that this would imply that there are
![]() $\alpha , \beta \in \mathbb {C}\setminus \{0\}$
, for which
$\alpha , \beta \in \mathbb {C}\setminus \{0\}$
, for which
![]() $P_i =\alpha Q_j + \beta Q_{j'}$
and then
$P_i =\alpha Q_j + \beta Q_{j'}$
and then
and the statement holds with
![]() $\gamma _i = \beta + \alpha $
, where we know by Theorem 4.9 that
$\gamma _i = \beta + \alpha $
, where we know by Theorem 4.9 that
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(\alpha a_j b_j + \beta a_{j'} b_{j'})=2$
.
$\operatorname {\mathrm {rank}}_{\text {s}}(\alpha a_j b_j + \beta a_{j'} b_{j'})=2$
.
So, let us assume that, for every
![]() $j \in [m_1]$
, there is
$j \in [m_1]$
, there is
![]() $t_j \in [m_2]$
such that
$t_j \in [m_2]$
such that
![]() $P_{t_j} \in \operatorname {span}\{{Q_j,P_i}\}$
. As
$P_{t_j} \in \operatorname {span}\{{Q_j,P_i}\}$
. As
![]() $5m_2+2<m_1$
, there must be
$5m_2+2<m_1$
, there must be
![]() $j'\neq j" \in [m_1]$
and
$j'\neq j" \in [m_1]$
and
![]() $t'\in [m_2]$
such that
$t'\in [m_2]$
such that
![]() $P_{t'} \in \operatorname {span}\{{Q_{j'}, P_i}\}$
and
$P_{t'} \in \operatorname {span}\{{Q_{j'}, P_i}\}$
and
![]() $ P_{t'} \in \operatorname {span}\{{Q_{j"}, P_i}\}$
. Since
$ P_{t'} \in \operatorname {span}\{{Q_{j"}, P_i}\}$
. Since
![]() $\mathcal {Q}$
is a set of pairwise linearly independent polynomials, we can deduce that
$\mathcal {Q}$
is a set of pairwise linearly independent polynomials, we can deduce that
![]() $\operatorname {span}\{{P_i, P_{t'}}\} = \operatorname {span}\{{Q_{j'}, Q_{j"}}\}$
. In particular, there exist
$\operatorname {span}\{{P_i, P_{t'}}\} = \operatorname {span}\{{Q_{j'}, Q_{j"}}\}$
. In particular, there exist
![]() $\alpha , \beta \in \mathbb {C}$
, for which
$\alpha , \beta \in \mathbb {C}$
, for which
![]() $P_i =\alpha Q_j + \beta Q_{j'}$
, which, as we already showed, implies what we wanted to prove.
$P_i =\alpha Q_j + \beta Q_{j'}$
, which, as we already showed, implies what we wanted to prove.
For simplicity, rescale
![]() $P_i$
so that
$P_i$
so that
![]() $P_i = \gamma _i Q_o+L_i$
with
$P_i = \gamma _i Q_o+L_i$
with
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(L_i)=2$
and
$\operatorname {\mathrm {rank}}_{\text {s}}(L_i)=2$
and
![]() $\gamma _i \in \{0,1\}$
. Clearly,
$\gamma _i \in \{0,1\}$
. Clearly,
![]() ${\mathcal {Q}}$
still satisfies the conditions of Theorem 4.9 after this rescaling as it does not affect the vanishing conditions or linear independence.
${\mathcal {Q}}$
still satisfies the conditions of Theorem 4.9 after this rescaling as it does not affect the vanishing conditions or linear independence.
Claim 5.4. Let
![]() $\tilde {{\mathcal {Q}}}$
be a
$\tilde {{\mathcal {Q}}}$
be a
![]() $(Q_o,m_1,m_2)\text{-}set$
, where
$(Q_o,m_1,m_2)\text{-}set$
, where
![]() ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
. Let
${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
. Let
![]() $P=\gamma Q_o + L\in {\mathcal {Q}_{\neg \text {prod}}}$
. Let V be defined as
$P=\gamma Q_o + L\in {\mathcal {Q}_{\neg \text {prod}}}$
. Let V be defined as
-
• If
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
 $V=\text {Lin}(L)$
and in particular
$V=\text {Lin}(L)$
and in particular
 $\dim (V)\leq 4$
.
$\dim (V)\leq 4$
. -
• If
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$
, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$
, then
 $V=\text {Lin}(Q_o)+\text {Lin}(L)$
, so
$V=\text {Lin}(Q_o)+\text {Lin}(L)$
, so
 $\dim (V)\leq 202$
.
$\dim (V)\leq 202$
.
Then, for at least
![]() $m_1-2m_2 $
indices
$m_1-2m_2 $
indices
![]() $j\in [m_1]$
it holds that
$j\in [m_1]$
it holds that
![]() $a_j,b_j \in V $
. Furthermore, for
$a_j,b_j \in V $
. Furthermore, for
![]() $Q_i=\alpha _iQ_o+a_ib_i \in {\mathcal {Q}}_{\text {prod}}$
the only cases in which
$Q_i=\alpha _iQ_o+a_ib_i \in {\mathcal {Q}}_{\text {prod}}$
the only cases in which
![]() $\{a_i,b_i\}\not \subseteq V$
are
$\{a_i,b_i\}\not \subseteq V$
are
-
1. If
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then it must be the case that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then it must be the case that
 $Q_i$
and P span a polynomial
$Q_i$
and P span a polynomial
 $P_j \in {\mathcal {Q}}_{\neg \text {prod}}$
.
$P_j \in {\mathcal {Q}}_{\neg \text {prod}}$
. -
2. If
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
, then either
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
, then either
 $Q_i$
and P span a polynomial
$Q_i$
and P span a polynomial
 $P_j \in {\mathcal {Q}}_{\neg \text {prod}}$
or there are two linear functions
$P_j \in {\mathcal {Q}}_{\neg \text {prod}}$
or there are two linear functions
 $c,d$
such that
$c,d$
such that
 $P,Q_o,Q_j\in \left \langle {c,d}\right \rangle $
.
$P,Q_o,Q_j\in \left \langle {c,d}\right \rangle $
.
Remark 5.5. When
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, we actually get the result for
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, we actually get the result for
![]() $m_1-m_2$
many indices.
$m_1-m_2$
many indices.
The idea of the proof is to study for each
![]() $Q_j\in {\mathcal {Q}}_{\text {prod}}\cup {\mathcal {L}}$
what case of Theorem 3.1 it satisfies with some
$Q_j\in {\mathcal {Q}}_{\text {prod}}\cup {\mathcal {L}}$
what case of Theorem 3.1 it satisfies with some
![]() $P\in {\mathcal {Q}_{\neg \text {prod}}}$
. If
$P\in {\mathcal {Q}_{\neg \text {prod}}}$
. If
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)$
is high, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)$
is high, then
![]() $Q_o$
must ‘disappear’ from the equations and we trivially get
$Q_o$
must ‘disappear’ from the equations and we trivially get
![]() $a_j,b_j\in V=\text {Lin}(P)$
. When the rank of
$a_j,b_j\in V=\text {Lin}(P)$
. When the rank of
![]() $Q_o$
is low, the argument is slightly different. In this case, we let V also contain
$Q_o$
is low, the argument is slightly different. In this case, we let V also contain
![]() $\text {Lin}(Q_o)$
, and using this, we show
$\text {Lin}(Q_o)$
, and using this, we show
![]() $a_j,b_j\in V$
.
$a_j,b_j\in V$
.
Proof. Let
![]() $P = \gamma Q_o+L\in {\mathcal {Q}_{\neg \text {prod}}}$
, where
$P = \gamma Q_o+L\in {\mathcal {Q}_{\neg \text {prod}}}$
, where
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(L) =2$
. Let V be defined as in the statement of the theorem: We set
$\operatorname {\mathrm {rank}}_{\text {s}}(L) =2$
. Let V be defined as in the statement of the theorem: We set
![]() $V = \text {Lin}(L)$
when
$V = \text {Lin}(L)$
when
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
and
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
and
![]() $V =\text {Lin}(Q_o)+\text {Lin}(L)$
otherwise.
$V =\text {Lin}(Q_o)+\text {Lin}(L)$
otherwise.
Let
![]() $Q_j=\alpha _j Q_o +a_j b_j\in {\mathcal {Q}}_{\text {prod}}$
. We consider which case of Theorem 3.1 P and
$Q_j=\alpha _j Q_o +a_j b_j\in {\mathcal {Q}}_{\text {prod}}$
. We consider which case of Theorem 3.1 P and
![]() $Q_j$
satisfy.
$Q_j$
satisfy.
P and
![]() $Q_j$
satisfy Theorem 3.1(product-case):
$Q_j$
satisfy Theorem 3.1(product-case):
In this case, there are two linear forms c and d, and nonzero
![]() $\alpha , \beta \in \mathbb {C}$
, such that
$\alpha , \beta \in \mathbb {C}$
, such that
![]() $\alpha P + \beta Q_j = cd$
. Hence,
$\alpha P + \beta Q_j = cd$
. Hence,
As
![]() $\beta \alpha _j Q_o+\alpha P$
is a nontrivial linear combination of
$\beta \alpha _j Q_o+\alpha P$
is a nontrivial linear combination of
![]() $Q_o$
and P, we get from property 4 of Theorem 4.9 that
$Q_o$
and P, we get from property 4 of Theorem 4.9 that
![]() $2 \leq \operatorname {\mathrm {rank}}_{\text {s}}((\alpha \gamma +\beta \alpha _j)Q_o+\alpha L)$
. It follows that
$2 \leq \operatorname {\mathrm {rank}}_{\text {s}}((\alpha \gamma +\beta \alpha _j)Q_o+\alpha L)$
. It follows that
If
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
![]() $\alpha \gamma +\beta \alpha _j=0$
. Thus, regardless of
$\alpha \gamma +\beta \alpha _j=0$
. Thus, regardless of
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)$
, we get from Theorem 2.15 that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)$
, we get from Theorem 2.15 that
and in particular
![]() $a_j,b_j\in V$
.
$a_j,b_j\in V$
.
P and
![]() $Q_j$
satisfy Theorem 3.1(linear-case):
$Q_j$
satisfy Theorem 3.1(linear-case):
If
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then it must hold that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then it must hold that
![]() $\alpha _j = 0$
and
$\alpha _j = 0$
and
![]() $Q_j =a_j^2$
. By the rank condition on
$Q_j =a_j^2$
. By the rank condition on
![]() $Q_o$
, it also follows that
$Q_o$
, it also follows that
![]() $\gamma = 0$
, and therefore,
$\gamma = 0$
, and therefore,
![]() $a_j \in \text {Lin}(L) = V$
.
$a_j \in \text {Lin}(L) = V$
.
Consider the case
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
. There are two linear forms c and d such that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
. There are two linear forms c and d such that
![]() $Q_j,P\in \sqrt {\left \langle {c,d}\right \rangle }$
. This implies that
$Q_j,P\in \sqrt {\left \langle {c,d}\right \rangle }$
. This implies that
![]() $\operatorname {span}\{{c,d}\} \subseteq \text {Lin}(P) \subseteq V$
.
$\operatorname {span}\{{c,d}\} \subseteq \text {Lin}(P) \subseteq V$
.
If
![]() $Q_o$
is zero modulo c and d, then
$Q_o$
is zero modulo c and d, then
![]() $Q_{j},Q_o$
satisfy Theorem 3.1(linear-case), and from property 5 of Theorem 4.9, we know that there are at most
$Q_{j},Q_o$
satisfy Theorem 3.1(linear-case), and from property 5 of Theorem 4.9, we know that there are at most
![]() $m_2$
such
$m_2$
such
![]() $Q_j$
’s. Furthermore, as
$Q_j$
’s. Furthermore, as
![]() $c,d\in \text {Lin}(Q_o) \subset V$
, we obtain that
$c,d\in \text {Lin}(Q_o) \subset V$
, we obtain that
![]() $Q_j \in \left \langle {V}\right \rangle $
. Denote by
$Q_j \in \left \langle {V}\right \rangle $
. Denote by
![]() ${\mathcal {K}}$
the set of all
${\mathcal {K}}$
the set of all
![]() $Q_j$
that satisfy Theorem 3.1(linear-case) with
$Q_j$
that satisfy Theorem 3.1(linear-case) with
![]() $Q_o$
, and recall that
$Q_o$
, and recall that
![]() $|{\mathcal {K}}|\leq m_2$
.
$|{\mathcal {K}}|\leq m_2$
.
If
![]() $Q_o=Q_j-a_j b_j$
is not zero modulo
$Q_o=Q_j-a_j b_j$
is not zero modulo
![]() ${c,d}$
, then we obtain that
${c,d}$
, then we obtain that
![]() $Q_o\equiv _{c,d} -a_j b_j$
. Thus, there are linear forms
$Q_o\equiv _{c,d} -a_j b_j$
. Thus, there are linear forms
![]() $v_1,v_2\in \text {Lin}(Q_o)$
such that
$v_1,v_2\in \text {Lin}(Q_o)$
such that
![]() $a_j \equiv _{c,d} v_1$
and
$a_j \equiv _{c,d} v_1$
and
![]() $b_j \equiv _{c,d} v_2$
. In particular, as
$b_j \equiv _{c,d} v_2$
. In particular, as
![]() $\text {Lin}(Q_o)\cup \{c,d\}\subseteq V$
, it follows that
$\text {Lin}(Q_o)\cup \{c,d\}\subseteq V$
, it follows that
![]() $a_j,b_j\in V$
.
$a_j,b_j\in V$
.
P and
![]() $Q_j$
satisfy Theorem 3.1(prime-case):
$Q_j$
satisfy Theorem 3.1(prime-case):
Let P and
![]() $Q_j$
satisfy Theorem 3.1(prime-case) but not Theorem 3.1(product-case) (as we already handled this case), that is, they span another polynomial in
$Q_j$
satisfy Theorem 3.1(prime-case) but not Theorem 3.1(product-case) (as we already handled this case), that is, they span another polynomial in
![]() $\tilde {{\mathcal {Q}}}\setminus {\mathcal {L}}$
. If this polynomial is in
$\tilde {{\mathcal {Q}}}\setminus {\mathcal {L}}$
. If this polynomial is in
![]() ${\mathcal {Q}}_{\text {prod}}$
, then there exists
${\mathcal {Q}}_{\text {prod}}$
, then there exists
![]() $j' \in [m_1]$
such that
$j' \in [m_1]$
such that
![]() $Q_{j'}\in \operatorname {span}\{{P,Q_j}\}$
. In this case,
$Q_{j'}\in \operatorname {span}\{{P,Q_j}\}$
. In this case,
![]() $P = \alpha Q_j + \beta Q_{j'}$
, and as before, we conclude that
$P = \alpha Q_j + \beta Q_{j'}$
, and as before, we conclude that
![]() $a_{j'} ,b_{j'}, a_{j}, b_{j} \in V$
.
$a_{j'} ,b_{j'}, a_{j}, b_{j} \in V$
.
All that is left is to bound the number of
![]() $j\in [m_1]$
so that P and
$j\in [m_1]$
so that P and
![]() $Q_j$
span a polynomial in
$Q_j$
span a polynomial in
![]() ${\mathcal {Q}}_{\neg \text {prod}}$
. If there are more than
${\mathcal {Q}}_{\neg \text {prod}}$
. If there are more than
![]() $m_2$
such indices j, then, by the pigeonhole principle, for two of them, say
$m_2$
such indices j, then, by the pigeonhole principle, for two of them, say
![]() $j,j'$
, it must be the case that there is some
$j,j'$
, it must be the case that there is some
![]() $i \in [m_2]$
such that
$i \in [m_2]$
such that
![]() $P_{i}\in \operatorname {span}\{{P,Q_j}\}$
and
$P_{i}\in \operatorname {span}\{{P,Q_j}\}$
and
![]() $P_{i}\in \operatorname {span}\{{P,Q_{j'}}\}$
. As our polynomials are pairwise independent, this implies that
$P_{i}\in \operatorname {span}\{{P,Q_{j'}}\}$
. As our polynomials are pairwise independent, this implies that
![]() $P \in \operatorname {span}\{{Q_j,Q_{j'}}\}$
, and as before, we get that
$P \in \operatorname {span}\{{Q_j,Q_{j'}}\}$
, and as before, we get that
![]() $a_{j'},b_{j'}, a_{j},b_{j}\in V$
.
$a_{j'},b_{j'}, a_{j},b_{j}\in V$
.
It follows that the only case where
![]() $a_j,b_j\not \in V$
and P and
$a_j,b_j\not \in V$
and P and
![]() $Q_j$
satisfy Theorem 3.1(prime-case) is when
$Q_j$
satisfy Theorem 3.1(prime-case) is when
![]() $Q_j$
and P span a polynomial in
$Q_j$
and P span a polynomial in
![]() ${\mathcal {Q}}_{\neg \text {prod}}$
, and no other
${\mathcal {Q}}_{\neg \text {prod}}$
, and no other
![]() $Q_{j'}$
spans this polynomial with P. Therefore, there are at most
$Q_{j'}$
spans this polynomial with P. Therefore, there are at most
![]() $m_2$
such ‘bad’ j’s.
$m_2$
such ‘bad’ j’s.
To conclude, the only j’s for which
![]() $a_j,b_j\not \in V$
can come from
$a_j,b_j\not \in V$
can come from
![]() $Q_j\in {\mathcal {K}}$
(when
$Q_j\in {\mathcal {K}}$
(when
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
) and P and
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
) and P and
![]() $Q_j$
satisfy Theorem 3.1(linear-case)), or it is one of the bad
$Q_j$
satisfy Theorem 3.1(linear-case)), or it is one of the bad
![]() $Q_j$
when P and
$Q_j$
when P and
![]() $Q_j$
satisfy Theorem 3.1(prime-case), so in total there are at most
$Q_j$
satisfy Theorem 3.1(prime-case), so in total there are at most
![]() $2m_2$
bad indices. This also shows the ‘furthermore’ part of the claim.
$2m_2$
bad indices. This also shows the ‘furthermore’ part of the claim.
5.3 Global structure
Our goal in this subsection is proving that there exists a constant-dimensional linear space of linear forms V such that, for some
![]() $\alpha \in \{0,1\}$
, every polynomial
$\alpha \in \{0,1\}$
, every polynomial
![]() $F\in \tilde {{\mathcal {Q}}}$
(more or less) has the form
$F\in \tilde {{\mathcal {Q}}}$
(more or less) has the form
![]() $F = \alpha Q_o +F' + c(\varepsilon c + v )$
, where c is a linear form,
$F = \alpha Q_o +F' + c(\varepsilon c + v )$
, where c is a linear form,
![]() $\varepsilon \in \mathbb {C}$
,
$\varepsilon \in \mathbb {C}$
,
![]() $v\in V$
and
$v\in V$
and
![]() $F'\in \mathbb {C}[V]$
.
$F'\in \mathbb {C}[V]$
.
We remark that
![]() $\alpha =1$
if
$\alpha =1$
if
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
and
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
and
![]() $\alpha =0$
otherwise (as in the low-rank case we construct V so that
$\alpha =0$
otherwise (as in the low-rank case we construct V so that
![]() $\text {Lin}(Q_o)\subseteq V$
).
$\text {Lin}(Q_o)\subseteq V$
).
Formally, we prove the following claim.
Claim 5.6. Let
![]() $\tilde {{\mathcal {Q}}}$
be a
$\tilde {{\mathcal {Q}}}$
be a
![]() $(Q_o,m_1,m_2)\text{-}{set}$
. There exists a linear space of linear forms V such that
$(Q_o,m_1,m_2)\text{-}{set}$
. There exists a linear space of linear forms V such that
-
• If
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
 $\dim (V)=4$
, and
$\dim (V)=4$
, and -
• If
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$
, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$
, then
 $\dim (V)\leq 202$
,
$\dim (V)\leq 202$
,
and the following hold: Every polynomial
![]() $F\in \tilde {{\mathcal {Q}}}$
satisfies at least one of the following:
$F\in \tilde {{\mathcal {Q}}}$
satisfies at least one of the following:
-
1.
 $F\in \mathbb {C}[V]$
, or
$F\in \mathbb {C}[V]$
, or -
2.
 $F = c^2$
, for a linear form c, or
$F = c^2$
, for a linear form c, or -
3.
 $F\in \left \langle {V}\right \rangle $
(only when
$F\in \left \langle {V}\right \rangle $
(only when
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$
), or
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$
), or -
4.
 $F = \alpha Q_o +F' + c(\varepsilon c + v )$
, where c is a linear form,
$F = \alpha Q_o +F' + c(\varepsilon c + v )$
, where c is a linear form,
 $\varepsilon \in \mathbb {C}$
,
$\varepsilon \in \mathbb {C}$
,
 $v\in V$
and
$v\in V$
and
 $F'\in \mathbb {C}[V]$
. Furthermore,
$F'\in \mathbb {C}[V]$
. Furthermore,
 $\alpha =1$
if
$\alpha =1$
if
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
and
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
and
 $\alpha =0$
otherwise.
$\alpha =0$
otherwise.
The proof of the claim depends on the rank of
![]() $Q_o$
(we use different arguments in the high-rank case and in the low-rank case) and on whether
$Q_o$
(we use different arguments in the high-rank case and in the low-rank case) and on whether
![]() ${\mathcal {Q}}_{\neg \text {prod}}$
is empty or not. When
${\mathcal {Q}}_{\neg \text {prod}}$
is empty or not. When
![]() ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
, we show that the space V that we constructed in Theorem 5.4 is the required space. The idea is that V already ‘explains’ so much of the structure of
${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
, we show that the space V that we constructed in Theorem 5.4 is the required space. The idea is that V already ‘explains’ so much of the structure of
![]() $\tilde {{\mathcal {Q}}}$
that we can expand it to all polynomials in
$\tilde {{\mathcal {Q}}}$
that we can expand it to all polynomials in
![]() $\tilde {{\mathcal {Q}}}$
. When
$\tilde {{\mathcal {Q}}}$
. When
![]() ${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $
, the argument is different and does not rely on Theorem 5.4. Here, since all polynomials are of the form
${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $
, the argument is different and does not rely on Theorem 5.4. Here, since all polynomials are of the form
![]() $Q_o + a_jb_j$
(ignoring squares of linear functions), using the conclusion of Theorem 5.1 that the
$Q_o + a_jb_j$
(ignoring squares of linear functions), using the conclusion of Theorem 5.1 that the
![]() $V_i$
s intersect nontrivially, and Theorem 2.21 we easily get the claimed structure.
$V_i$
s intersect nontrivially, and Theorem 2.21 we easily get the claimed structure.
Proof. We analyze two cases: when
![]() ${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $
and the case
${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $
and the case
![]() ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
.
${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
.
The case
![]() ${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $
:
${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $
:
Let
Observe that, if
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
![]() ${\mathcal {I}}$
simply contains all
${\mathcal {I}}$
simply contains all
![]() $V_i$
s of dimension
$V_i$
s of dimension
![]() $2$
.
$2$
.
If
![]() ${\mathcal {I}}=\emptyset $
, then we can take
${\mathcal {I}}=\emptyset $
, then we can take
![]() $V=\{0\}$
when
$V=\{0\}$
when
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
or
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
or
![]() $V=\text {Lin}(Q_o)$
in the case
$V=\text {Lin}(Q_o)$
in the case
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$
. Indeed, Theorem 2.18 implies that in this case every polynomial is of the form
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$
. Indeed, Theorem 2.18 implies that in this case every polynomial is of the form
![]() $F = \alpha Q_o +F' + c^2$
, with
$F = \alpha Q_o +F' + c^2$
, with
![]() $\alpha =\mathbb {1}_{\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100}$
.
$\alpha =\mathbb {1}_{\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100}$
.
Assume then that
![]() ${\mathcal {I}}\neq \emptyset $
. Combining Theorem 5.2 and Theorem 2.21, we get that either
${\mathcal {I}}\neq \emptyset $
. Combining Theorem 5.2 and Theorem 2.21, we get that either
![]() $\dim (\bigcup _{i\in {\mathcal {I}}} V_i) \leq 3$
or
$\dim (\bigcup _{i\in {\mathcal {I}}} V_i) \leq 3$
or
![]() $\dim (\bigcap _{i\in {\mathcal {I}}} V_i) =1$
.
$\dim (\bigcap _{i\in {\mathcal {I}}} V_i) =1$
.
If
![]() $\dim (\bigcup _{i\in {\mathcal {I}}} V_i) \leq 3$
, then we define
$\dim (\bigcup _{i\in {\mathcal {I}}} V_i) \leq 3$
, then we define
![]() $V'=\bigcup _{i\in {\mathcal {I}}} V_i$
. If
$V'=\bigcup _{i\in {\mathcal {I}}} V_i$
. If
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)<100$
, then we let
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)<100$
, then we let
![]() $V=V'+\text {Lin}(Q_o)$
so that
$V=V'+\text {Lin}(Q_o)$
so that
![]() $\dim (V)\leq 201$
, and when
$\dim (V)\leq 201$
, and when
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)\geq 100$
, we let
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)\geq 100$
, we let
![]() $V=V'$
and
$V=V'$
and
![]() $\dim (V)=3$
. It is clear that V satisfies the requirement when
$\dim (V)=3$
. It is clear that V satisfies the requirement when
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
. So assume
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
. So assume
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)<100$
. Clearly, every
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)<100$
. Clearly, every
![]() $Q_i$
such that
$Q_i$
such that
![]() $i\in {\mathcal {I}}$
has the claimed structure as
$i\in {\mathcal {I}}$
has the claimed structure as
![]() $\text {Lin}(Q_i)\subseteq V$
. Consider any polynomial
$\text {Lin}(Q_i)\subseteq V$
. Consider any polynomial
![]() $Q_i=Q_o+a_ib_i\in {\mathcal {Q}_{\text {prod}}}$
such that
$Q_i=Q_o+a_ib_i\in {\mathcal {Q}_{\text {prod}}}$
such that
![]() $i\not \in {\mathcal {I}}$
. As
$i\not \in {\mathcal {I}}$
. As
![]() $i\not \in {\mathcal {I}}$
, we either have that
$i\not \in {\mathcal {I}}$
, we either have that
![]() $\dim (V_i)=1$
, in which case
$\dim (V_i)=1$
, in which case
![]() $Q_i$
has the claimed form, or for some nonzero
$Q_i$
has the claimed form, or for some nonzero
![]() $\beta $
,
$\beta $
,
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o +\beta a_i b_i)<3$
. In the later case, as
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o +\beta a_i b_i)<3$
. In the later case, as
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 2$
, Theorem 2.17 implies that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 2$
, Theorem 2.17 implies that
![]() $\operatorname {span}\{{a_i,b_i}\}\cap \text {Lin}(Q_o)\neq \{0\}$
and in particular
$\operatorname {span}\{{a_i,b_i}\}\cap \text {Lin}(Q_o)\neq \{0\}$
and in particular
![]() $\operatorname {span}\{{a_i,b_i}\}\cap V\neq \{0\}$
. Thus, in any of these cases, V has the required property.
$\operatorname {span}\{{a_i,b_i}\}\cap V\neq \{0\}$
. Thus, in any of these cases, V has the required property.
Consider now the case
![]() $\dim (\bigcap _{i=1}^m V_i) =1$
. Let w be such that
$\dim (\bigcap _{i=1}^m V_i) =1$
. Let w be such that
![]() $\operatorname {span}\{{w}\} = \dim (\bigcap _{i=1}^m V_i)$
. As before, it is not hard to see that, if we define V as
$\operatorname {span}\{{w}\} = \dim (\bigcap _{i=1}^m V_i)$
. As before, it is not hard to see that, if we define V as
![]() $V=\operatorname {span}\{{w}\}$
in the high rank case and
$V=\operatorname {span}\{{w}\}$
in the high rank case and
![]() $V=\operatorname {span}\{{w}\}+\text {Lin}(Q_o)$
in the low rank case, then V has the required property.
$V=\operatorname {span}\{{w}\}+\text {Lin}(Q_o)$
in the low rank case, then V has the required property.
The case
![]() ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
:
${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $
:
Let
![]() $P=\gamma Q+L\in {\mathcal {Q}_{\neg \text {prod}}}$
and V be as in the statement of Theorem 5.4. We next show that V satisfies the claim. Let
$P=\gamma Q+L\in {\mathcal {Q}_{\neg \text {prod}}}$
and V be as in the statement of Theorem 5.4. We next show that V satisfies the claim. Let
![]() ${\mathcal {J}} = \lbrace Q_j\mid j\in [m_1]\text { and }a_j,b_j \in V\rbrace $
. Theorem 5.4 implies that
${\mathcal {J}} = \lbrace Q_j\mid j\in [m_1]\text { and }a_j,b_j \in V\rbrace $
. Theorem 5.4 implies that
![]() $|{\mathcal {J}}|\geq m_1-2m_2$
(and if
$|{\mathcal {J}}|\geq m_1-2m_2$
(and if
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, then
![]() $|{\mathcal {J}}|\geq m_1-m_2$
).
$|{\mathcal {J}}|\geq m_1-m_2$
).
We first note that every
![]() $P_i \in {\mathcal {J}}$
satisfies the claim with
$P_i \in {\mathcal {J}}$
satisfies the claim with
![]() $P^{\prime }_i = a_ib_i$
and
$P^{\prime }_i = a_ib_i$
and
![]() $v_i=c_i =0$
, and clearly the claim trivially holds for
$v_i=c_i =0$
, and clearly the claim trivially holds for
![]() $Q_i \in {\mathcal {L}}$
.
$Q_i \in {\mathcal {L}}$
.
Consider
![]() $Q_i \in {\mathcal {Q}}_{\text {prod}} \setminus {\mathcal {J}}$
. By the ‘furthermore’ part of Theorem 5.4 one of two cases must happen: Either
$Q_i \in {\mathcal {Q}}_{\text {prod}} \setminus {\mathcal {J}}$
. By the ‘furthermore’ part of Theorem 5.4 one of two cases must happen: Either
![]() $Q_i$
and P span a polynomial
$Q_i$
and P span a polynomial
![]() $P_j \in {\mathcal {Q}}_{\neg \text {prod}}$
or, when
$P_j \in {\mathcal {Q}}_{\neg \text {prod}}$
or, when
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
, there are two linear functions
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
, there are two linear functions
![]() $c,d$
such that
$c,d$
such that
![]() $P,Q_o,Q_j\in \left \langle {c,d}\right \rangle $
. Observe that, in the latter case, as
$P,Q_o,Q_j\in \left \langle {c,d}\right \rangle $
. Observe that, in the latter case, as
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
, we have that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
, we have that
![]() $\operatorname {span}\{{c,d}\}\subseteq \text {Lin}(Q_o)\subseteq V$
. In particular,
$\operatorname {span}\{{c,d}\}\subseteq \text {Lin}(Q_o)\subseteq V$
. In particular,
![]() $Q_i\in \left \langle {V}\right \rangle $
, and the claim follows. So assume that
$Q_i\in \left \langle {V}\right \rangle $
, and the claim follows. So assume that
![]() $Q_i$
and P span a polynomial
$Q_i$
and P span a polynomial
![]() $P_j \in {\mathcal {Q}}_{\neg \text {prod}}$
. Namely, there are
$P_j \in {\mathcal {Q}}_{\neg \text {prod}}$
. Namely, there are
![]() $\alpha ,\beta \in \mathbb {C}\setminus \{0\}$
such that
$\alpha ,\beta \in \mathbb {C}\setminus \{0\}$
such that
![]() $P_j = \alpha P + \beta Q_i$
. Theorem 5.3 implies that
$P_j = \alpha P + \beta Q_i$
. Theorem 5.3 implies that
![]() $P_j = \gamma _j Q_o + L_j$
, where
$P_j = \gamma _j Q_o + L_j$
, where
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(L_j)=2$
, and thus,
$\operatorname {\mathrm {rank}}_{\text {s}}(L_j)=2$
, and thus,
From property 4 of Theorem 4.9, we conclude that
![]() $\operatorname {\mathrm {rank}}_{\text {s}}((\alpha \gamma -\beta -\gamma _j )Q_o + \alpha L)\geq 2=\operatorname {\mathrm {rank}}_{\text {s}}(L_j)$
. Theorem 2.17 implies that
$\operatorname {\mathrm {rank}}_{\text {s}}((\alpha \gamma -\beta -\gamma _j )Q_o + \alpha L)\geq 2=\operatorname {\mathrm {rank}}_{\text {s}}(L_j)$
. Theorem 2.17 implies that
![]() $\operatorname {span}\{{a_i,b_i}\} \cap V \neq \{{\mathbf {0}}\}$
, and therefore, there is
$\operatorname {span}\{{a_i,b_i}\} \cap V \neq \{{\mathbf {0}}\}$
, and therefore, there is
![]() $v_i\in V$
such that, without loss of generality,
$v_i\in V$
such that, without loss of generality,
![]() $b_i = \varepsilon _i a_i + v_i$
, for some constant
$b_i = \varepsilon _i a_i + v_i$
, for some constant
![]() $\varepsilon _i$
. Thus, the claimed statement holds for
$\varepsilon _i$
. Thus, the claimed statement holds for
![]() $Q_i$
with
$Q_i$
with
![]() $c_i = a_i$
and
$c_i = a_i$
and
![]() $Q^{\prime }_i = 0$
. That is,
$Q^{\prime }_i = 0$
. That is,
![]() $Q_i = Q_o + 0+ a_i(\varepsilon _i a_i + v_i )$
.
$Q_i = Q_o + 0+ a_i(\varepsilon _i a_i + v_i )$
.
Consider a polynomial
![]() $P_i=\gamma _iQ_o+L_i\in {\mathcal {Q}}_{\neg \text {prod}}$
. It is clear that, if
$P_i=\gamma _iQ_o+L_i\in {\mathcal {Q}}_{\neg \text {prod}}$
. It is clear that, if
![]() $P_i$
satisfies Theorem 3.1(linear-case) with any polynomial in
$P_i$
satisfies Theorem 3.1(linear-case) with any polynomial in
![]() ${\mathcal {J}}$
, then
${\mathcal {J}}$
, then
![]() $P\in \left \langle {V}\right \rangle $
(observe that in this case we must have
$P\in \left \langle {V}\right \rangle $
(observe that in this case we must have
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
).
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
).
Next, assume that
![]() $P_i$
satisfies Theorem 3.1(product-case) with at least
$P_i$
satisfies Theorem 3.1(product-case) with at least
![]() $2$
polynomials whose indices are in
$2$
polynomials whose indices are in
![]() ${\mathcal {J}}$
. Let
${\mathcal {J}}$
. Let
![]() $Q_j,Q_{j'}$
be two such polynomials. There are four linear forms,
$Q_j,Q_{j'}$
be two such polynomials. There are four linear forms,
![]() $c,d,e$
and f and scalars
$c,d,e$
and f and scalars
![]() $\varepsilon _j, \varepsilon _{j'}$
such that
$\varepsilon _j, \varepsilon _{j'}$
such that
Therefore,
As
![]() $\varepsilon _j a_jb_j-\varepsilon _{j'}a_{j'}b_{j'}\in \mathbb {C}[V]$
, rank arguments imply that
$\varepsilon _j a_jb_j-\varepsilon _{j'}a_{j'}b_{j'}\in \mathbb {C}[V]$
, rank arguments imply that
![]() $\text {Lin}(cd -ef)\subseteq V$
. From Theorem 2.19 and equation (5.5), we get that, without loss of generality,
$\text {Lin}(cd -ef)\subseteq V$
. From Theorem 2.19 and equation (5.5), we get that, without loss of generality,
![]() $d = \varepsilon c + v$
for some
$d = \varepsilon c + v$
for some
![]() $v \in V$
and
$v \in V$
and
![]() $\varepsilon \in \mathbb {C}$
. Thus,
$\varepsilon \in \mathbb {C}$
. Thus,
![]() $P_i = cd -\varepsilon _j Q_j = c(\varepsilon c+v) -\varepsilon _jQ_o -\varepsilon _j a_j b_j$
, and it is clear that it has the required structure.
$P_i = cd -\varepsilon _j Q_j = c(\varepsilon c+v) -\varepsilon _jQ_o -\varepsilon _j a_j b_j$
, and it is clear that it has the required structure.
The only case left is when
![]() $P_i$
satisfies Theorem 3.1(prime-case) with all (except possibly one of the) polynomials whose indices are in
$P_i$
satisfies Theorem 3.1(prime-case) with all (except possibly one of the) polynomials whose indices are in
![]() ${\mathcal {J}}$
.
${\mathcal {J}}$
.
If
![]() $P_i$
and
$P_i$
and
![]() $Q_j$
, for
$Q_j$
, for
![]() $j\in {\mathcal {J}}$
span another polynomial
$j\in {\mathcal {J}}$
span another polynomial
![]() $Q_{j'}$
such that
$Q_{j'}$
such that
![]() $j'\in {\mathcal {J}}$
, then, as before,
$j'\in {\mathcal {J}}$
, then, as before,
![]() $\text {Lin}(P)\subseteq V$
. Similarly, if P and
$\text {Lin}(P)\subseteq V$
. Similarly, if P and
![]() $Q_j$
span a polynomial
$Q_j$
span a polynomial
![]() $Q_{j'}\in {\mathcal {L}}$
, then
$Q_{j'}\in {\mathcal {L}}$
, then
![]() $P = \alpha Q_j + \beta a_{j'}^2$
, and hence, it also satisfies the claim.
$P = \alpha Q_j + \beta a_{j'}^2$
, and hence, it also satisfies the claim.
Hence, for P to fail to satisfy the claim, it must be the case that every polynomial
![]() $Q_j$
, for
$Q_j$
, for
![]() $j\in {\mathcal {J}}$
, that satisfies Theorem 3.1(prime-case) with P, does not span with P any polynomial in
$j\in {\mathcal {J}}$
, that satisfies Theorem 3.1(prime-case) with P, does not span with P any polynomial in
![]() $\{Q_j \mid j\in {\mathcal {J}}\} \cup {\mathcal {L}}$
. Thus, it must span with P a polynomial in
$\{Q_j \mid j\in {\mathcal {J}}\} \cup {\mathcal {L}}$
. Thus, it must span with P a polynomial in
![]() $\{Q_j \mid j\in [m_1]\setminus {\mathcal {J}}\} \cup {\mathcal {Q}}_{\neg \text {prod}}$
. Observe that by pairwise linear independence, if two polynomials from
$\{Q_j \mid j\in [m_1]\setminus {\mathcal {J}}\} \cup {\mathcal {Q}}_{\neg \text {prod}}$
. Observe that by pairwise linear independence, if two polynomials from
![]() ${\mathcal {J}}$
span the same polynomial with P, then P is in their span, and we are done. However, notice that
${\mathcal {J}}$
span the same polynomial with P, then P is in their span, and we are done. However, notice that
As
![]() $P_i$
satisfies Theorem 3.1(prime-case) with at least
$P_i$
satisfies Theorem 3.1(prime-case) with at least
![]() $|{\mathcal {J}}|-1$
polynomials whose indices are in
$|{\mathcal {J}}|-1$
polynomials whose indices are in
![]() ${\mathcal {J}}$
, we get from the pigeonhole principle that there is some polynomial
${\mathcal {J}}$
, we get from the pigeonhole principle that there is some polynomial
![]() $F\in \tilde {Q}$
and two indices
$F\in \tilde {Q}$
and two indices
![]() $j,j'\in {\mathcal {J}}$
such that
$j,j'\in {\mathcal {J}}$
such that
![]() $F\in \operatorname {span}\{{P_i,Q_j}\}\cap \operatorname {span}\{{P_i,Q_{j'}}\}$
. As before, pairwise linear independence implies that
$F\in \operatorname {span}\{{P_i,Q_j}\}\cap \operatorname {span}\{{P_i,Q_{j'}}\}$
. As before, pairwise linear independence implies that
![]() $P_i\in \operatorname {span}\{{Q_j,Q_{j'}}\}$
, and we are done.
$P_i\in \operatorname {span}\{{Q_j,Q_{j'}}\}$
, and we are done.
5.4 Completing the proof
Now that we know that all polynomials in
![]() $\tilde {Q}$
satisfy the structure of Theorem 5.6, we can finish the proof of Theorem 4.10.
$\tilde {Q}$
satisfy the structure of Theorem 5.6, we can finish the proof of Theorem 4.10.
The main remaining step is proving that all linear polynomials c appearing in the statement of Theorem 4.10 form a Sylvester–Gallai configuration, and we will be done.
There is a small issue though. When the rank of
![]() $Q_o$
is small, some polynomials can belong to
$Q_o$
is small, some polynomials can belong to
![]() $\left \langle {V}\right \rangle $
and are not captured by the outlined approach. This difference requires us to handle the low- and high-rank cases separately.
$\left \langle {V}\right \rangle $
and are not captured by the outlined approach. This difference requires us to handle the low- and high-rank cases separately.
Theorem 4.10 follows from Corollaries 5.8 and 5.10 below.
5.4.1 The case
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
Consider the representation guaranteed in Theorem 4.10, and let
 $$\begin{align*}\begin{aligned} {\mathcal{S}} = \lbrace c_i \mid \text{there is } P_i\in\tilde{{\mathcal{Q}}} \text{ such that either } P_i = c_i^2 \text{ or, for some } P^{\prime}_i \text{ defined over } V, \\ P_i= Q_o +P^{\prime}_i + c_i(\varepsilon_i c_i + v_i) \rbrace . \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} {\mathcal{S}} = \lbrace c_i \mid \text{there is } P_i\in\tilde{{\mathcal{Q}}} \text{ such that either } P_i = c_i^2 \text{ or, for some } P^{\prime}_i \text{ defined over } V, \\ P_i= Q_o +P^{\prime}_i + c_i(\varepsilon_i c_i + v_i) \rbrace . \end{aligned} \end{align*}$$
Clearly, in order to bound the dimension of
![]() $\tilde {{\mathcal {Q}}}$
, it is enough to bound the dimension of
$\tilde {{\mathcal {Q}}}$
, it is enough to bound the dimension of
![]() ${\mathcal {S}}$
. We do so by proving that
${\mathcal {S}}$
. We do so by proving that
![]() ${\mathcal {S}}$
satisfies the conditions of Sylvester–Gallai theorem modulo V and thus have dimension at most
${\mathcal {S}}$
satisfies the conditions of Sylvester–Gallai theorem modulo V and thus have dimension at most
![]() $3+\dim (V)=7$
.
$3+\dim (V)=7$
.
Claim 5.7. Assume that
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, and let
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, and let
![]() ${\mathcal {S}}$
be defined as above. Let
${\mathcal {S}}$
be defined as above. Let
![]() $c_i, c_j \in {\mathcal {S}}$
be such that
$c_i, c_j \in {\mathcal {S}}$
be such that
![]() $c_i \notin V$
and
$c_i \notin V$
and
![]() $c_j \notin \operatorname {span}\{{c_i,V}\}$
. Then, there is
$c_j \notin \operatorname {span}\{{c_i,V}\}$
. Then, there is
![]() $c_k \in {\mathcal {S}}$
such that
$c_k \in {\mathcal {S}}$
such that
![]() $c_k \in \operatorname {span}\{{c_i,c_j,V}\}$
and
$c_k \in \operatorname {span}\{{c_i,c_j,V}\}$
and
![]() $c_k \notin \operatorname {span}\{{c_i,V}\}\cup \operatorname {span}\{{c_j,V}\}$
.
$c_k \notin \operatorname {span}\{{c_i,V}\}\cup \operatorname {span}\{{c_j,V}\}$
.
Proof. Following the notation of Theorem 5.6, we either have
![]() $Q_i = Q_o + Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i )$
, for
$Q_i = Q_o + Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i )$
, for
![]() $Q^{\prime }_i\in \mathbb {C}[V]$
, or
$Q^{\prime }_i\in \mathbb {C}[V]$
, or
![]() $Q_i = c_i^2$
. We consider which case of Theorem 3.1
$Q_i = c_i^2$
. We consider which case of Theorem 3.1
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
satisfy and what structure they have.
$Q_j$
satisfy and what structure they have.
Assume
![]() $Q_i = Q_o + Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i )$
and
$Q_i = Q_o + Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i )$
and
![]() $Q_j = Q_o + Q^{\prime }_j + c_j(\varepsilon _jc_j + v_j )$
. As argued before, since the rank of
$Q_j = Q_o + Q^{\prime }_j + c_j(\varepsilon _jc_j + v_j )$
. As argued before, since the rank of
![]() $Q_o$
is large, they cannot satisfy Theorem 3.1(linear-case). We consider the remaining cases:
$Q_o$
is large, they cannot satisfy Theorem 3.1(linear-case). We consider the remaining cases:
-
•
 $Q_i,Q_j$
satisfy Theorem 3.1(prime-case): There is
$Q_i,Q_j$
satisfy Theorem 3.1(prime-case): There is
 $Q_k \in \tilde {{\mathcal {Q}}}$
such that
$Q_k \in \tilde {{\mathcal {Q}}}$
such that
 $Q_k \in \operatorname {span}\{{Q_i,Q_j}\}$
.By assumption, for some scalars
$Q_k \in \operatorname {span}\{{Q_i,Q_j}\}$
.By assumption, for some scalars
 $\alpha ,\beta $
we have that (5.6)If
$\alpha ,\beta $
we have that (5.6)If $$ \begin{align} Q_k = \alpha(Q_o + Q^{\prime}_i + c_i(\varepsilon_i c_i + v_i )) + \beta(Q_o + Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j)) . \end{align} $$
$$ \begin{align} Q_k = \alpha(Q_o + Q^{\prime}_i + c_i(\varepsilon_i c_i + v_i )) + \beta(Q_o + Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j)) . \end{align} $$
 $Q_k$
depends only on V, then we would get a contradiction to the choice of
$Q_k$
depends only on V, then we would get a contradiction to the choice of
 $c_i,c_j$
. Indeed, in this case, we have that Rank arguments imply that
$c_i,c_j$
. Indeed, in this case, we have that Rank arguments imply that $$ \begin{align*} (\alpha+\beta)Q_o = Q_k - \alpha( Q^{\prime}_i + c_i(\varepsilon_i c_i + v_i )) - \beta( Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j)). \end{align*} $$
$$ \begin{align*} (\alpha+\beta)Q_o = Q_k - \alpha( Q^{\prime}_i + c_i(\varepsilon_i c_i + v_i )) - \beta( Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j)). \end{align*} $$
 $\alpha +\beta =0$
, and therefore, which implies that
$\alpha +\beta =0$
, and therefore, which implies that $$ \begin{align*} \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) = Q_k - \alpha Q^{\prime}_i - \beta Q^{\prime}_j \in\mathbb{C}[V], \end{align*} $$
$$ \begin{align*} \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) = Q_k - \alpha Q^{\prime}_i - \beta Q^{\prime}_j \in\mathbb{C}[V], \end{align*} $$
 $c_i$
and
$c_i$
and
 $c_j$
are linearly dependent modulo V in contradiction.
$c_j$
are linearly dependent modulo V in contradiction.
If
 $Q_k = c_k^2$
, then Theorem 2.20 implies that
$Q_k = c_k^2$
, then Theorem 2.20 implies that
 $c_k\in \operatorname {span}\{{c_i,c_j,V}\}$
.
$c_k\in \operatorname {span}\{{c_i,c_j,V}\}$
.We therefore assume that
 $Q_k$
is not a function of V alone, and it is not a square of a linear function. Denote
$Q_k$
is not a function of V alone, and it is not a square of a linear function. Denote
 $Q_k = \gamma _k Q_o + Q^{\prime }_k + c_k(\varepsilon _k c_k + v_k)$
. Equation 5.6 implies that As
$Q_k = \gamma _k Q_o + Q^{\prime }_k + c_k(\varepsilon _k c_k + v_k)$
. Equation 5.6 implies that As $$ \begin{align*} (\gamma_k - \alpha-\beta)Q_o = \alpha Q^{\prime}_i + \beta Q^{\prime}_j - Q^{\prime}_k + \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) - c_k(\varepsilon_k c_k + v_k). \end{align*} $$
$$ \begin{align*} (\gamma_k - \alpha-\beta)Q_o = \alpha Q^{\prime}_i + \beta Q^{\prime}_j - Q^{\prime}_k + \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) - c_k(\varepsilon_k c_k + v_k). \end{align*} $$
 $\alpha Q^{\prime }_i + \beta Q^{\prime }_j - Q^{\prime }_k$
is a polynomial defined over V, its rank is smaller than
$\alpha Q^{\prime }_i + \beta Q^{\prime }_j - Q^{\prime }_k$
is a polynomial defined over V, its rank is smaller than
 $4$
, and thus, combined with the fact that
$4$
, and thus, combined with the fact that
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o) \geq 100$
, we get that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o) \geq 100$
, we get that
 $ (\gamma _k - \alpha -\beta ) = 0$
and We conclude again from Theorem 2.20 that
$ (\gamma _k - \alpha -\beta ) = 0$
and We conclude again from Theorem 2.20 that $$\begin{align*}Q^{\prime}_k -\alpha Q^{\prime}_i - \beta Q^{\prime}_j = \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) - c_k(\varepsilon_k c_k + v_k) .\end{align*}$$
$$\begin{align*}Q^{\prime}_k -\alpha Q^{\prime}_i - \beta Q^{\prime}_j = \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) - c_k(\varepsilon_k c_k + v_k) .\end{align*}$$
 $c_k\in \operatorname {span}\{{c_i,c_j,V}\}$
.
$c_k\in \operatorname {span}\{{c_i,c_j,V}\}$
.
-
•
 $Q_i,Q_j$
satisfy Theorem 3.1(product-case): There are linear forms
$Q_i,Q_j$
satisfy Theorem 3.1(product-case): There are linear forms
 $e,f$
such that for nonzero scalars
$e,f$
such that for nonzero scalars
 $\alpha ,\beta $
,
$\alpha ,\beta $
,
 $\alpha Q_i + \beta Q_j = ef$
. In particular, From rank argument, we get that
$\alpha Q_i + \beta Q_j = ef$
. In particular, From rank argument, we get that $$\begin{align*}(\alpha + \beta ) Q_o = ef - \alpha Q^{\prime}_i - \beta Q^{\prime}_j - \alpha c_i(\varepsilon_i c_i + v_i ) - \beta c_j(\varepsilon_j c_j + v_j).\end{align*}$$
$$\begin{align*}(\alpha + \beta ) Q_o = ef - \alpha Q^{\prime}_i - \beta Q^{\prime}_j - \alpha c_i(\varepsilon_i c_i + v_i ) - \beta c_j(\varepsilon_j c_j + v_j).\end{align*}$$
 $\alpha + \beta = 0$
, and from Theorem 2.20, we conclude that, without loss of generality,
$\alpha + \beta = 0$
, and from Theorem 2.20, we conclude that, without loss of generality,
 $e = \mu c_i + \eta c_j +v_e$
, where
$e = \mu c_i + \eta c_j +v_e$
, where
 $\mu , \eta \neq 0$
. We also assume without loss of generality that
$\mu , \eta \neq 0$
. We also assume without loss of generality that
 $Q_i=Q_j+ef$
.
$Q_i=Q_j+ef$
.
Since
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, it follows that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
, it follows that
 $Q_j$
is irreducible even after setting
$Q_j$
is irreducible even after setting
 $e=0$
. It follows that, if a product of irreducible quadratics satisfy then, after setting
$e=0$
. It follows that, if a product of irreducible quadratics satisfy then, after setting $$ \begin{align*} \prod_k A_k \in \sqrt{\left \langle{Q_i,Q_j}\right \rangle} = \sqrt{\left \langle{ef,Q_j}\right \rangle}, \end{align*} $$
$$ \begin{align*} \prod_k A_k \in \sqrt{\left \langle{Q_i,Q_j}\right \rangle} = \sqrt{\left \langle{ef,Q_j}\right \rangle}, \end{align*} $$
 $e=0$
, some
$e=0$
, some
 $A_k$
is divisible by
$A_k$
is divisible by
 ${Q_j}|_{e=0}$
. Thus, there is a multiplicand that is equal to
${Q_j}|_{e=0}$
. Thus, there is a multiplicand that is equal to
 $ \gamma Q_j + ed$
for some linear form d and scalar
$ \gamma Q_j + ed$
for some linear form d and scalar
 $\gamma $
. In particular, there must be a polynomial
$\gamma $
. In particular, there must be a polynomial
 $Q_k \in \tilde {\mathcal {Q}}\setminus \{Q_i,Q_j\}$
such that
$Q_k \in \tilde {\mathcal {Q}}\setminus \{Q_i,Q_j\}$
such that
 $Q_k = \gamma Q_j + ed$
. If
$Q_k = \gamma Q_j + ed$
. If
 $\gamma = 0$
, then it must hold that
$\gamma = 0$
, then it must hold that
 $Q_k = a_k^2 = ed$
and thus
$Q_k = a_k^2 = ed$
and thus
 $a_k \sim e$
, and the statement holds. If
$a_k \sim e$
, and the statement holds. If
 $\gamma = 1$
, then we can assume without loss of generality that
$\gamma = 1$
, then we can assume without loss of generality that
 $Q_k = Q_j + ed$
. Thus, Rearranging, we get
$Q_k = Q_j + ed$
. Thus, Rearranging, we get $$ \begin{align*} Q_o + Q^{\prime}_k + c_k(\varepsilon_k c_k + v_k) = Q_k = Q_j + ed = Q_o+ Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j) + (\mu c_i + \eta c_j + v_e)d . \end{align*} $$
As the right-hand side vanishes modulo
$$ \begin{align*} Q_o + Q^{\prime}_k + c_k(\varepsilon_k c_k + v_k) = Q_k = Q_j + ed = Q_o+ Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j) + (\mu c_i + \eta c_j + v_e)d . \end{align*} $$
As the right-hand side vanishes modulo $$ \begin{align*} c_k(\varepsilon_k c_k + v_k) = (Q^{\prime}_j-Q^{\prime}_k) + c_j(\varepsilon_j c_j + v_j) + (\mu c_i + \eta c_j + v_e)d . \end{align*} $$
$$ \begin{align*} c_k(\varepsilon_k c_k + v_k) = (Q^{\prime}_j-Q^{\prime}_k) + c_j(\varepsilon_j c_j + v_j) + (\mu c_i + \eta c_j + v_e)d . \end{align*} $$
 $\operatorname {span}\{{c_i,c_j,V}\}$
, it follows that
$\operatorname {span}\{{c_i,c_j,V}\}$
, it follows that
 $c_k\in \operatorname {span}\{{c_i,c_j,V}\}$
. Observe that, if
$c_k\in \operatorname {span}\{{c_i,c_j,V}\}$
. Observe that, if
 $c_k\in \operatorname {span}\{{c_j,V}\}$
, then this implies that However, since
$c_k\in \operatorname {span}\{{c_j,V}\}$
, then this implies that However, since $$ \begin{align*} (\mu c_i + \eta c_j + v_e)d\in\mathbb{C}[V,c_j]. \end{align*} $$
$$ \begin{align*} (\mu c_i + \eta c_j + v_e)d\in\mathbb{C}[V,c_j]. \end{align*} $$
 $d\neq 0$
(as otherwise we would have
$d\neq 0$
(as otherwise we would have
 $Q_k\sim Q_j$
), this stands in contradiction to the fact that
$Q_k\sim Q_j$
), this stands in contradiction to the fact that
 $\mu \neq 0$
and
$\mu \neq 0$
and
 $c_i\not \in \operatorname {span}\{{c_j,V}\}$
. As
$c_i\not \in \operatorname {span}\{{c_j,V}\}$
. As
 $Q_i=Q_j+ef$
, we get that We cannot have
$Q_i=Q_j+ef$
, we get that We cannot have $$ \begin{align*} c_k(\varepsilon_k c_k + v_k) = (Q^{\prime}_j-Q^{\prime}_k) + c_i(\varepsilon_i c_i + v_i) + (\mu c_i + \eta c_j + v_e)(d-f) . \end{align*} $$
$$ \begin{align*} c_k(\varepsilon_k c_k + v_k) = (Q^{\prime}_j-Q^{\prime}_k) + c_i(\varepsilon_i c_i + v_i) + (\mu c_i + \eta c_j + v_e)(d-f) . \end{align*} $$
 $d=f$
as this would give
$d=f$
as this would give
 $Q_i=Q_k$
. Thus, a similar argument implies that
$Q_i=Q_k$
. Thus, a similar argument implies that
 $c_k\not \in \operatorname {span}\{{c_i,V}\}$
. In conclusion,
$c_k\not \in \operatorname {span}\{{c_i,V}\}$
. In conclusion,
 $c_k\in \operatorname {span}\{{c_i,c_j,V}\}\setminus (\operatorname {span}\{{c_i,V}\}\cup \operatorname {span}\{{c_j,V}\})$
as claimed.
$c_k\in \operatorname {span}\{{c_i,c_j,V}\}\setminus (\operatorname {span}\{{c_i,V}\}\cup \operatorname {span}\{{c_j,V}\})$
as claimed.
Now, let us consider the case where without loss of generality,
![]() $Q_i = Q_o +Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i)$
and
$Q_i = Q_o +Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i)$
and
![]() $Q_j = c_j^2$
. In this case, the polynomials satisfy Theorem 3.1(product-case) as
$Q_j = c_j^2$
. In this case, the polynomials satisfy Theorem 3.1(product-case) as
![]() $0 \cdot Q_i + Q_j = c_j^2$
. Similarly to the previous argument, it holds that there is
$0 \cdot Q_i + Q_j = c_j^2$
. Similarly to the previous argument, it holds that there is
![]() $Q_k$
such that
$Q_k$
such that
![]() $Q_k = \gamma Q_i + c_j e$
. If
$Q_k = \gamma Q_i + c_j e$
. If
![]() $\gamma =0$
, then
$\gamma =0$
, then
![]() $Q_k$
is reducible and therefore a square of a linear form which is a multiple of
$Q_k$
is reducible and therefore a square of a linear form which is a multiple of
![]() $c_j$
, in contradiction to pairwise linear independence. Hence, we have that
$c_j$
, in contradiction to pairwise linear independence. Hence, we have that
![]() $\gamma \neq 0$
. If
$\gamma \neq 0$
. If
![]() $Q_k$
is defined only on the linear functions in V, then it is of rank smaller than
$Q_k$
is defined only on the linear functions in V, then it is of rank smaller than
![]() $\dim (V) \leq 4$
, which will result in a contradiction to the rank assumption on
$\dim (V) \leq 4$
, which will result in a contradiction to the rank assumption on
![]() $Q_o$
. Thus,
$Q_o$
. Thus,
![]() $Q_k = Q_o + Q^{\prime }_k + c_k(\varepsilon _k c_k + v_k)$
and
$Q_k = Q_o + Q^{\prime }_k + c_k(\varepsilon _k c_k + v_k)$
and
![]() $\gamma = 1$
. It follows that
$\gamma = 1$
. It follows that
Hence,
An argument similar to the last one shows that
![]() $c_k \in \operatorname {span}\{{V, c_i, c_j}\}$
and that
$c_k \in \operatorname {span}\{{V, c_i, c_j}\}$
and that
![]() $c_k \notin \operatorname {span}\{{V, c_j}\}\cup \operatorname {span}\{{V, c_i}\}$
, as we wanted to show.
$c_k \notin \operatorname {span}\{{V, c_j}\}\cup \operatorname {span}\{{V, c_i}\}$
, as we wanted to show.
The last structure we have to consider is the case where
![]() $Q_i = c_i^2, Q_j = c_j^2$
. In this case, the ideal
$Q_i = c_i^2, Q_j = c_j^2$
. In this case, the ideal
 $\sqrt {\left \langle {c_i^2,c_j^2}\right \rangle } = \left \langle {c_i,c_j}\right \rangle $
is prime, and therefore, there is
$\sqrt {\left \langle {c_i^2,c_j^2}\right \rangle } = \left \langle {c_i,c_j}\right \rangle $
is prime, and therefore, there is
![]() $Q_k \in \left \langle {c_i,c_j}\right \rangle $
. This means that
$Q_k \in \left \langle {c_i,c_j}\right \rangle $
. This means that
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) \leq 2$
. If
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) \leq 2$
. If
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) = 1$
, then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) = 1$
, then
![]() $Q_k = c_k^2$
and the statement holds. If
$Q_k = c_k^2$
and the statement holds. If
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) = 2$
, then Theorem 5.6 implies that
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) = 2$
, then Theorem 5.6 implies that
![]() $Q_k$
is in
$Q_k$
is in
![]() $\mathbb {C}[V]$
, from which we get that
$\mathbb {C}[V]$
, from which we get that
![]() $c_i,c_j \in V$
in contradiction to our assumptions.
$c_i,c_j \in V$
in contradiction to our assumptions.
Corollary 5.8. Let
![]() $\tilde {{\mathcal {Q}}}$
be a
$\tilde {{\mathcal {Q}}}$
be a
![]() $(Q_o,m_1,m_2)\text{-}\mathrm{set}$
, where
$(Q_o,m_1,m_2)\text{-}\mathrm{set}$
, where
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
. Then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$
. Then
![]() $\dim (\tilde {{\mathcal {Q}}}) \leq 29$
.
$\dim (\tilde {{\mathcal {Q}}}) \leq 29$
.
Proof. Observe that definition of
![]() ${\mathcal {S}}$
and Theorem 5.6 imply that
${\mathcal {S}}$
and Theorem 5.6 imply that
![]() $\dim \left ( \tilde {{\mathcal {Q}}}\right )\leq 1+{\dim (\operatorname {span}\{{V+{\mathcal {S}}}\})+1 \choose 2}$
. As Theorem 5.7 implies that
$\dim \left ( \tilde {{\mathcal {Q}}}\right )\leq 1+{\dim (\operatorname {span}\{{V+{\mathcal {S}}}\})+1 \choose 2}$
. As Theorem 5.7 implies that
![]() $\dim ({\mathcal {S}}+V)\leq 7$
, we get that
$\dim ({\mathcal {S}}+V)\leq 7$
, we get that
![]() $\dim \left ( \tilde {{\mathcal {Q}}}\right )\leq 29$
.
$\dim \left ( \tilde {{\mathcal {Q}}}\right )\leq 29$
.
5.4.2 The case
 $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
Observe that Theorem 5.6 implies that when
![]() $\operatorname {rank}(Q_o)<100$
then
$\operatorname {rank}(Q_o)<100$
then
![]() $\text {Lin}(Q_o)\subseteq V$
, and thus, any polynomial
$\text {Lin}(Q_o)\subseteq V$
, and thus, any polynomial
![]() $Q_i \in \tilde {{\mathcal {Q}}}$
satisfies that either
$Q_i \in \tilde {{\mathcal {Q}}}$
satisfies that either
![]() $Q_i \in \left \langle {V}\right \rangle $
or there is a linear form
$Q_i \in \left \langle {V}\right \rangle $
or there is a linear form
![]() $a_i$
such that
$a_i$
such that
![]() $\text {Lin}(Q_i) \subseteq \operatorname {span}\{{V,a_i}\}$
.
$\text {Lin}(Q_i) \subseteq \operatorname {span}\{{V,a_i}\}$
.
Let
![]() $\Delta =\dim (V)\leq 202$
. Fix some basis of V,
$\Delta =\dim (V)\leq 202$
. Fix some basis of V,
![]() $V=\operatorname {span}\{{v_1,\ldots ,v_{\Delta }}\}$
. Let
$V=\operatorname {span}\{{v_1,\ldots ,v_{\Delta }}\}$
. Let
![]() ${\boldsymbol {\alpha }}\in \mathbb {C}^{\Delta }$
(recall Theorem 2.24) be such that, if two polynomials in
${\boldsymbol {\alpha }}\in \mathbb {C}^{\Delta }$
(recall Theorem 2.24) be such that, if two polynomials in
![]() $T_{{\boldsymbol {\alpha }}, V}(\tilde {{\mathcal {Q}}})$
share a common factor, then it is a polynomial in z. Note that by Theorem 2.26 such
$T_{{\boldsymbol {\alpha }}, V}(\tilde {{\mathcal {Q}}})$
share a common factor, then it is a polynomial in z. Note that by Theorem 2.26 such
![]() ${\boldsymbol {\alpha }}$
exists. Thus, each
${\boldsymbol {\alpha }}$
exists. Thus, each
![]() $P\in \tilde {{\mathcal {Q}}}$
, satisfies that either
$P\in \tilde {{\mathcal {Q}}}$
, satisfies that either
![]() $T_{{\boldsymbol {\alpha }}, V}(P)=\alpha _P z^2$
or
$T_{{\boldsymbol {\alpha }}, V}(P)=\alpha _P z^2$
or
![]() $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(P))\subseteq \operatorname {span}\{{z,a_P}\}$
, for some linear form
$\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(P))\subseteq \operatorname {span}\{{z,a_P}\}$
, for some linear form
![]() $a_P$
independent of z. It follows that every polynomial in
$a_P$
independent of z. It follows that every polynomial in
![]() $T_{{\boldsymbol {\alpha }}, V}(\tilde {{\mathcal {Q}}})$
is reducible. We next show that
$T_{{\boldsymbol {\alpha }}, V}(\tilde {{\mathcal {Q}}})$
is reducible. We next show that
![]() ${\mathcal {S}} = \{a_P \mid P\in \tilde {\mathcal {Q}}\}$
satisfies the conditions of Sylvester–Gallai theorem modulo z.
${\mathcal {S}} = \{a_P \mid P\in \tilde {\mathcal {Q}}\}$
satisfies the conditions of Sylvester–Gallai theorem modulo z.
Claim 5.9. Let
![]() ${\mathcal {S}}$
be defined as above. Let
${\mathcal {S}}$
be defined as above. Let
![]() $a_1, a_2 \in {\mathcal {S}}$
such that
$a_1, a_2 \in {\mathcal {S}}$
such that
![]() $a_1\not \in \operatorname {span}\{{z}\}$
and
$a_1\not \in \operatorname {span}\{{z}\}$
and
![]() $a_2 \notin \operatorname {span}\{{z,a_1}\}$
. Then, there is
$a_2 \notin \operatorname {span}\{{z,a_1}\}$
. Then, there is
![]() $a_3\in {\mathcal {S}}$
such that
$a_3\in {\mathcal {S}}$
such that
![]() $a_3 \in \operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$
.
$a_3 \in \operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$
.
Proof. Let
![]() $Q_1$
be such that
$Q_1$
be such that
![]() $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_1)) \subseteq \operatorname {span}\{{z,a_1}\}$
yet
$\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_1)) \subseteq \operatorname {span}\{{z,a_1}\}$
yet
![]() $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_1)) \not \subseteq \operatorname {span}\{{z}\}$
. Similarly, let
$\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_1)) \not \subseteq \operatorname {span}\{{z}\}$
. Similarly, let
![]() $Q_2$
be such that
$Q_2$
be such that
![]() $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_2)) \subseteq \operatorname {span}\{{z,a_2}\}$
and
$\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_2)) \subseteq \operatorname {span}\{{z,a_2}\}$
and
![]() $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_2)) \not \subseteq \operatorname {span}\{{z}\}$
. As
$\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_2)) \not \subseteq \operatorname {span}\{{z}\}$
. As
![]() $a_1,a_2\in {\mathcal {S}}$
, there must be such
$a_1,a_2\in {\mathcal {S}}$
, there must be such
![]() $Q_1,Q_2$
. By choice of
$Q_1,Q_2$
. By choice of
![]() $Q_1$
, there is a factor of
$Q_1$
, there is a factor of
![]() $T_{{\boldsymbol {\alpha }},V}(Q_1)$
of the form
$T_{{\boldsymbol {\alpha }},V}(Q_1)$
of the form
![]() $\gamma _1 z + \delta _1 a_1$
, where
$\gamma _1 z + \delta _1 a_1$
, where
![]() $\delta _1\neq 0$
. Similarly there is a factor of
$\delta _1\neq 0$
. Similarly there is a factor of
![]() $T_{{\boldsymbol {\alpha }},V}(Q_2)$
of the form
$T_{{\boldsymbol {\alpha }},V}(Q_2)$
of the form
![]() $\gamma _2 z + \delta _2 a_2$
, where
$\gamma _2 z + \delta _2 a_2$
, where
![]() $\delta _2\neq 0$
. It follows that
$\delta _2\neq 0$
. It follows that
![]() $\sqrt {\left \langle {T_{{\boldsymbol {\alpha }},V}(Q_1), T_{{\boldsymbol {\alpha }},V}(Q_2)}\right \rangle } \subseteq \left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
. Indeed, it is clear that, for
$\sqrt {\left \langle {T_{{\boldsymbol {\alpha }},V}(Q_1), T_{{\boldsymbol {\alpha }},V}(Q_2)}\right \rangle } \subseteq \left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
. Indeed, it is clear that, for
![]() $i\in \{1,2\}$
,
$i\in \{1,2\}$
,
![]() ${T_{{\boldsymbol {\alpha }},V}(Q_i)}\in \left \langle {\gamma _i z + \delta _i a_i}\right \rangle $
. Hence,
${T_{{\boldsymbol {\alpha }},V}(Q_i)}\in \left \langle {\gamma _i z + \delta _i a_i}\right \rangle $
. Hence,
![]() $\sqrt {\left \langle {T_{{\boldsymbol {\alpha }},V}(Q_1), T_{{\boldsymbol {\alpha }},V}(Q_2)}\right \rangle } \subseteq \sqrt {\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle }=\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
, where equality holds since
$\sqrt {\left \langle {T_{{\boldsymbol {\alpha }},V}(Q_1), T_{{\boldsymbol {\alpha }},V}(Q_2)}\right \rangle } \subseteq \sqrt {\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle }=\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
, where equality holds since
![]() $\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
is a prime ideal.
$\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
is a prime ideal.
We know that there are
![]() $Q_3,Q_4,Q_5,Q_6\in {\mathcal {Q}}$
such that
$Q_3,Q_4,Q_5,Q_6\in {\mathcal {Q}}$
such that
As
![]() $T_{{\boldsymbol {\alpha }},V}$
is a ring homomorphism, it follows that
$T_{{\boldsymbol {\alpha }},V}$
is a ring homomorphism, it follows that
Primality of
![]() $\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
implies that, without loss of generality,
$\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
implies that, without loss of generality,
![]() $T_{{\boldsymbol {\alpha }},V}(Q_3)\in \left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
. It cannot be the case that
$T_{{\boldsymbol {\alpha }},V}(Q_3)\in \left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $
. It cannot be the case that
![]() $T_{{\boldsymbol {\alpha }},V}(Q_3)\in \left \langle {\gamma _i z + \delta _i a_i}\right \rangle $
for any
$T_{{\boldsymbol {\alpha }},V}(Q_3)\in \left \langle {\gamma _i z + \delta _i a_i}\right \rangle $
for any
![]() $i \in \{1,2\}$
because otherwise this will imply that
$i \in \{1,2\}$
because otherwise this will imply that
![]() $T_{{\boldsymbol {\alpha }},V}(Q_3)$
and
$T_{{\boldsymbol {\alpha }},V}(Q_3)$
and
![]() $T_{{\boldsymbol {\alpha }},V}(Q_i)$
share a common factor that is not a polynomial in z, in contradiction to our choice of
$T_{{\boldsymbol {\alpha }},V}(Q_i)$
share a common factor that is not a polynomial in z, in contradiction to our choice of
![]() $T_{{\boldsymbol {\alpha }}, V}$
. This means that there is a factor of
$T_{{\boldsymbol {\alpha }}, V}$
. This means that there is a factor of
![]() $T_{{\boldsymbol {\alpha }},V}(Q_3)$
that is in
$T_{{\boldsymbol {\alpha }},V}(Q_3)$
that is in
![]() $\operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$
. Consequently,
$\operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$
. Consequently,
![]() $a_3 \in \operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$
as we wanted to prove.
$a_3 \in \operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$
as we wanted to prove.
Corollary 5.10. Let
![]() $\tilde {{\mathcal {Q}}}$
be a
$\tilde {{\mathcal {Q}}}$
be a
![]() $(Q_o,m_1,m_2)$
-set, where
$(Q_o,m_1,m_2)$
-set, where
![]() $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
. Then
$\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$
. Then
![]() $\dim (\tilde {{\mathcal {Q}}}) \leq 8\dim (V)^2$
, where V is as in Theorem 5.6.
$\dim (\tilde {{\mathcal {Q}}}) \leq 8\dim (V)^2$
, where V is as in Theorem 5.6.
Proof. Theorem 5.9 shows that
![]() ${\mathcal {S}}$
satisfies the conditions of Theorem 2.10, and therefore,
${\mathcal {S}}$
satisfies the conditions of Theorem 2.10, and therefore,
![]() $\dim ({\mathcal {S}})\leq 3$
. Repeating the analysis of the claim for linearly independent
$\dim ({\mathcal {S}})\leq 3$
. Repeating the analysis of the claim for linearly independent
![]() ${{\boldsymbol {\alpha }}}_1,\ldots , {{\boldsymbol {\alpha }}}_{\Delta }$
, we conclude from Theorem 2.29 that
${{\boldsymbol {\alpha }}}_1,\ldots , {{\boldsymbol {\alpha }}}_{\Delta }$
, we conclude from Theorem 2.29 that
![]() $\dim (\text {Lin}(\tilde {\mathcal {Q}})) \leq (3+1)\Delta $
, and thus
$\dim (\text {Lin}(\tilde {\mathcal {Q}})) \leq (3+1)\Delta $
, and thus
![]() $\dim (\tilde {{\mathcal {Q}}}) \leq {4\Delta \choose 2}+\Delta \leq 8\Delta ^2$
.
$\dim (\tilde {{\mathcal {Q}}}) \leq {4\Delta \choose 2}+\Delta \leq 8\Delta ^2$
.
6 Conclusions and future research
In this work, we solved Theorem 1.2 in the case where all the polynomials are irreducible and of degree at most
![]() $2$
. This result directly relates to the problem of obtaining deterministic algorithms for testing identities of
$2$
. This result directly relates to the problem of obtaining deterministic algorithms for testing identities of
![]() $\Sigma ^{[3]}\Pi ^{[d]}\Sigma \Pi ^{[2]}$
circuits. As mentioned in section 1, to get a PIT algorithm a colored version of this result is required. Such a result was obtained in [Reference Peleg and Shpilka17].
$\Sigma ^{[3]}\Pi ^{[d]}\Sigma \Pi ^{[2]}$
circuits. As mentioned in section 1, to get a PIT algorithm a colored version of this result is required. Such a result was obtained in [Reference Peleg and Shpilka17].
Our proof of Theorem 1.4 used the robust version of the Sylvester–Gallai theorem of [Reference Barak, Dvir, Wigderson and Yehudayoff1, Reference Dvir, Saraf and Wigderson8] (Theorem 2.7). We believe that in order to extend our results to higher degrees a similar robust version for quadratic polynomials may be useful.
Problem 6.1. Let
![]() $\delta \in (0,1]$
. Can we bound the linear dimension (as a function of
$\delta \in (0,1]$
. Can we bound the linear dimension (as a function of
![]() $\delta $
) of a set of polynomials
$\delta $
) of a set of polynomials
![]() $Q_1,\ldots ,Q_m\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
that satisfy the following property: For every
$Q_1,\ldots ,Q_m\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
that satisfy the following property: For every
![]() $i\in [m]$
, there exist at least
$i\in [m]$
, there exist at least
![]() $\delta m$
values of
$\delta m$
values of
![]() $j \in [m]$
such that for each such j there is
$j \in [m]$
such that for each such j there is
![]() ${\mathcal {K}}_j \subset [m]$
, where
${\mathcal {K}}_j \subset [m]$
, where
![]() $i,j \notin {\mathcal {K}}_j$
and
$i,j \notin {\mathcal {K}}_j$
and
![]() $\prod _{k\in {\mathcal {K}}_j} Q_k \in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$
?
$\prod _{k\in {\mathcal {K}}_j} Q_k \in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$
?
In subsequent work [Reference Peleg, Shpilka, Goaoc and Kerber18, Reference Garg, Oliveira and Sengupta11], the following simpler version of Problem 6.1 was proved.
Theorem 6.2. Let
![]() $\delta \in (0,1]$
. Let
$\delta \in (0,1]$
. Let
![]() ${\mathcal {Q}}=\{Q_1,\ldots ,Q_m\}\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be irreducible polynomials of degree at most
${\mathcal {Q}}=\{Q_1,\ldots ,Q_m\}\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$
be irreducible polynomials of degree at most
![]() $2$
satisfying the following property: For every
$2$
satisfying the following property: For every
![]() $i\in [m]$
, there exist at least
$i\in [m]$
, there exist at least
![]() $\delta m$
values of
$\delta m$
values of
![]() $j \in [m]$
such that for each such j there is
$j \in [m]$
such that for each such j there is
![]() $k\in [m]\setminus \{i,j\}$
with
$k\in [m]\setminus \{i,j\}$
with
![]() $Q_k \in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$
. Then,
$Q_k \in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$
. Then,
![]() $\dim (\operatorname {span}\{{{\mathcal {Q}}}\})=O(1/\delta ^{16})$
.
$\dim (\operatorname {span}\{{{\mathcal {Q}}}\})=O(1/\delta ^{16})$
.
Another interesting question is giving a tight bound in Theorem 1.4. A careful analysis of the proof shows that we can bound the dimension of the set
![]() ${\mathcal {T}}$
satisfying the conditions in Theorem 1.4 by
${\mathcal {T}}$
satisfying the conditions in Theorem 1.4 by
![]() $c\leq 20,000$
. This is a very loose bound, and we believe that it can be improved. It is also an interesting task to present examples with as large dimension as possible.
$c\leq 20,000$
. This is a very loose bound, and we believe that it can be improved. It is also an interesting task to present examples with as large dimension as possible.
In our opinion, the most interesting problem is extending our result to higher degrees. Another important problem is to extend Theorem 3.1 to the case where
![]() $\prod _{k\in {\mathcal {K}}}Q_k \in \sqrt {\left \langle {A_1,\ldots ,A_e}\right \rangle }$
, for a constant
$\prod _{k\in {\mathcal {K}}}Q_k \in \sqrt {\left \langle {A_1,\ldots ,A_e}\right \rangle }$
, for a constant
![]() $e>2$
.
$e>2$
.
In this paper, we only considered polynomials over the complex numbers. However, we believe (though we did not check the details) that a similar approach should work over positive characteristic as well. Observe that over positive characteristic we expect the dimension of the set to scale like
![]() $O(\log |{\mathcal {Q}}|)$
, as for such fields a weaker version of Sylvester–Gallai theorem holds.
$O(\log |{\mathcal {Q}}|)$
, as for such fields a weaker version of Sylvester–Gallai theorem holds.
Theorem 6.3 (Corollary
 $1.3$
in [Reference Bhattacharyya, Dvir, Saraf and Shpilka3]).
$1.3$
in [Reference Bhattacharyya, Dvir, Saraf and Shpilka3]).
Let
![]() $V=\lbrace {{\mathbf {v}}}_1,\ldots , {{\mathbf {v}}}_{m}\rbrace \subset \mathbb {F}_p^d$
be a set of m vectors, no two of which are linearly dependent. Suppose that, for every
$V=\lbrace {{\mathbf {v}}}_1,\ldots , {{\mathbf {v}}}_{m}\rbrace \subset \mathbb {F}_p^d$
be a set of m vectors, no two of which are linearly dependent. Suppose that, for every
![]() $i,j\in [m]$
, there exists
$i,j\in [m]$
, there exists
![]() $k\in [m]$
such that
$k\in [m]$
such that
![]() ${\mathbf {v}}_i,{\mathbf {v}}_j,{\mathbf {v}}_k$
are linearly dependent. Then, for every
${\mathbf {v}}_i,{\mathbf {v}}_j,{\mathbf {v}}_k$
are linearly dependent. Then, for every
![]() $\varepsilon>0$
$\varepsilon>0$
Acknowledgments
We are grateful to Rafael Mendes de Oliveira and to an anonymous reviewer for bringing [Reference Colliot-Thélène, Sansuc and Swinnerton-Dyer5] and [Reference Vallance, Hodge and Pedoe13] to our attention. We also thank Rafael for helpful conversations regarding the proof of [Reference Colliot-Thélène, Sansuc and Swinnerton-Dyer5]. We thank the anonymous reviewers for comments that helped us improve and simplify the presentation of our results.
Conflict of Interest
The authors have no conflict of interest to declare.
Funding statement
The research leading to these results has received funding from the Israel Science Foundation (grant number 552/16) and from the Len Blavatnik and the Blavatnik Family foundation. Part of this work was done while the second author was a visiting professor at NYU.