The history of relevance logic cannot be written without mentioning J. Michael Dunn who played a prominent role in shaping this area of logic. In the late twentieth century, he was a doyen with a world-class reputation in the field of philosophical logic. Dunn’s research also encompassed logics outside of relevance logic, from 2-valued first-order logic to quantum logic and substructural logics such as the Lambek calculi, intuitionistic logic, linear logic, etc. Each of the disciplines of philosophy, mathematics, and computer science has been impacted in intrinsic ways by some of the theorems proved by Dunn.
Jon Michael Dunn was born in Fort Wayne, Indiana, on June 19, 1941, and he passed away on April 5, 2021, in Bloomington, Indiana. After attending high schools in Fort Wayne and Lafayette, he obtained an AB degree in philosophy from Oberlin College, Ohio, in 1963. Dunn completed his Ph.D. Thesis entitled The Algebra of Intensional Logics at Pittsburgh University in 1966; his thesis supervisor was Nuel D. Belnap. In 1969, Dunn was appointed an associate professor in the Department of Philosophy at Indiana University in Bloomington, Indiana, and he stayed on the faculty at IU until 2007, when he retired as University Dean of the School of Informatics, Oscar R. Ewing Professor of Philosophy, Professor of Informatics, Professor of Computer Science, and Core Faculty in Cognitive Science. Dunn supervised 14 Ph.D. students in logic and 3 Ph.D. students in other areas of philosophy. He taught advanced graduate courses in logic, including courses on 2-valued logic (metalogic), modal logic, algebraic logics, and substructural logics. Dunn was the founding dean of the School of Informatics, and he served in other administrative positions such as Chair of the Department of Philosophy and Associate Dean of the College of Arts and Sciences in previous years. Dunn held multiple research grants and visiting positions at universities in the US, Europe, and Australia. Dunn, for his contributions to Indiana University, was honored by the IU Provost Medallion in 2007. The state of Indiana bestowed on Dunn the rank and title of Sagamore of the Wabash the same year. Dunn was elected a Fellow of the American Academy of Arts and Sciences in 2010.
The logic of relevant implication
![]() $\mathbf {R}$
combines Church’s “weak implication” with lattice connectives and De Morgan negation. Alternatively,
$\mathbf {R}$
combines Church’s “weak implication” with lattice connectives and De Morgan negation. Alternatively,
![]() $\mathbf {R}$
results from Ackermann’s system
$\mathbf {R}$
results from Ackermann’s system
![]() $\boldsymbol {\Pi '}$
by omitting a rule (the so-called
$\boldsymbol {\Pi '}$
by omitting a rule (the so-called
![]() $\gamma $
rule) and adding permutation. Dunn started to investigate
$\gamma $
rule) and adding permutation. Dunn started to investigate
![]() $\mathbf {R}$
from an algebraic point of view in his Ph.D. thesis [Reference Dunn14]. This research continued the study of distributive lattices with De Morgan negation already underway in [Reference Anderson and Belnap1, Reference Belnap and Spencer4, Reference Białynicki-Birula and Rasiowa5, Reference Dunn and Belnap35, Reference Kalman43]. Dunn showed that
$\mathbf {R}$
from an algebraic point of view in his Ph.D. thesis [Reference Dunn14]. This research continued the study of distributive lattices with De Morgan negation already underway in [Reference Anderson and Belnap1, Reference Belnap and Spencer4, Reference Białynicki-Birula and Rasiowa5, Reference Dunn and Belnap35, Reference Kalman43]. Dunn showed that
![]() $\boldsymbol{\mathit{4}}$
, the four-element lattice with two incomparable elements on which negation has fixed points, plays a fundamental role among De Morgan lattices, and hence, for first-degree entailments fde; (the implication-free fragment of
$\boldsymbol{\mathit{4}}$
, the four-element lattice with two incomparable elements on which negation has fixed points, plays a fundamental role among De Morgan lattices, and hence, for first-degree entailments fde; (the implication-free fragment of
![]() $\mathbf {R}$
and of the logic of entailment
$\mathbf {R}$
and of the logic of entailment
![]() $\mathbf {E}$
). Dunn proved—using methods similar to those Stone utilized in his representation of Boolean algebras—that every De Morgan lattice is embeddable into a product of
$\mathbf {E}$
). Dunn proved—using methods similar to those Stone utilized in his representation of Boolean algebras—that every De Morgan lattice is embeddable into a product of
![]() $\boldsymbol{\mathit{4}}$
, that is, into
$\boldsymbol{\mathit{4}}$
, that is, into
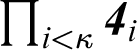 $\prod _{i<\kappa }\boldsymbol{\mathit{4}}_i$
, where
$\prod _{i<\kappa }\boldsymbol{\mathit{4}}_i$
, where
![]() $\kappa \le \lambda ^2$
and
$\kappa \le \lambda ^2$
and
![]() $\lambda $
is the cardinality of the De Morgan lattice. Whenever possible, Dunn generalized theorems to complete lattices, complete homomorphisms, complete embeddings, and similar notions, which, strictly speaking, go beyond the purely algebraic approach. He also defined a new interpretation for fde that relies on pairs of sets of situations. Later, Dunn defined the four values (true, false, both, and neither) that emerge in the interpretation of fde as subsets of
$\lambda $
is the cardinality of the De Morgan lattice. Whenever possible, Dunn generalized theorems to complete lattices, complete homomorphisms, complete embeddings, and similar notions, which, strictly speaking, go beyond the purely algebraic approach. He also defined a new interpretation for fde that relies on pairs of sets of situations. Later, Dunn defined the four values (true, false, both, and neither) that emerge in the interpretation of fde as subsets of
![]() $\{\,T,F\}$
, and Belnap provided motivations for these values by appeal to databases. Nowadays, this logic is often referred to as Dunn–Belnap (or Belnap–Dunn) logic (cf. [Reference Omori and Wansing48]). The algebraization of
$\{\,T,F\}$
, and Belnap provided motivations for these values by appeal to databases. Nowadays, this logic is often referred to as Dunn–Belnap (or Belnap–Dunn) logic (cf. [Reference Omori and Wansing48]). The algebraization of
![]() $\mathbf {R}$
revolves around two concepts: residuation and the intensional truth constant (denoted by
$\mathbf {R}$
revolves around two concepts: residuation and the intensional truth constant (denoted by
![]() $\boldsymbol {t}$
). Relevant implication (
$\boldsymbol {t}$
). Relevant implication (
![]() $\to $
) is not a residual of conjunction (
$\to $
) is not a residual of conjunction (
![]() $\land $
)—unlike intuitionistic implication. Dunn introduced an intensional conjunction connective (
$\land $
)—unlike intuitionistic implication. Dunn introduced an intensional conjunction connective (
![]() $\circ $
) and treated
$\circ $
) and treated
![]() $\to $
as its residual. He defined De Morgan semi-groups and showed that the Lindenbaum algebra of
$\to $
as its residual. He defined De Morgan semi-groups and showed that the Lindenbaum algebra of
![]() $\mathbf {R}$
is not free in the class of De Morgan semi-groups. However, once
$\mathbf {R}$
is not free in the class of De Morgan semi-groups. However, once
![]() $\boldsymbol {t}$
is added to
$\boldsymbol {t}$
is added to
![]() $\mathbf {R}$
(conservatively), the Lindenbaum algebra of
$\mathbf {R}$
(conservatively), the Lindenbaum algebra of
![]() $\mathbf {R}^{\boldsymbol {t}}$
is free in the class of De Morgan monoids. This algebraization of propositional
$\mathbf {R}^{\boldsymbol {t}}$
is free in the class of De Morgan monoids. This algebraization of propositional
![]() $\mathbf {R}$
parallels the algebraization of 2-valued propositional logic as a Boolean algebra.
$\mathbf {R}$
parallels the algebraization of 2-valued propositional logic as a Boolean algebra.
Dunn and Belnap proved in [Reference Dunn and Belnap36] that 2-valued first-order logic (fol) is incomplete with the substitutional interpretation of quantifiers. The latter approach to quantification is popular in some introductory logic courses, presumably, because it bypasses the function that assigns elements of the domain to variables. A simple form of this incompleteness is practically obvious to anybody who is familiar with standard definitions of the language and the interpretation of fol; however, [Reference Dunn and Belnap36] proved incompleteness in a stronger sense using Gödel’s incompleteness theorem. Dunn and Belnap also pointed out a notion of logical consequence that is not subject to this sort of incompleteness. To wit, logical consequence that is invariant under extensions of the language by new name constants circumvents the crucial step in the incompleteness argument; this notion is pivotal in Henkin-style completeness proofs for first-order logics.
Algebraic investigations of relevance logics by Dunn led to a proof of the admissibility of
![]() $\gamma $
in joint work with Robert K. Meyer. The
$\gamma $
in joint work with Robert K. Meyer. The
![]() $\gamma $
rule (as a rule of inference) was omitted from Ackermann’s
$\gamma $
rule (as a rule of inference) was omitted from Ackermann’s
![]() $\mathbf {\Pi }\boldsymbol {{}^{\prime }}$
calculus giving the logic
$\mathbf {\Pi }\boldsymbol {{}^{\prime }}$
calculus giving the logic
![]() $\mathbf {E}$
. [Reference Meyer and Michael Dunn47] showed that if both A and
$\mathbf {E}$
. [Reference Meyer and Michael Dunn47] showed that if both A and
![]() $\mathop {\sim } A\lor B$
are theorems of
$\mathop {\sim } A\lor B$
are theorems of
![]() $\mathbf {E}$
, then so is B; similarly, for
$\mathbf {E}$
, then so is B; similarly, for
![]() $\mathbf {R}$
and
$\mathbf {R}$
and
![]() $\mathbf {T}$
(the logic of ticket entailment). This resolved one of the most intriguing open problems concerning
$\mathbf {T}$
(the logic of ticket entailment). This resolved one of the most intriguing open problems concerning
![]() $\mathbf {E}$
(cf. [30] and [47]).
$\mathbf {E}$
(cf. [30] and [47]).
![]() $\mathop {\sim } A\lor B$
may be written as
$\mathop {\sim } A\lor B$
may be written as
![]() $A\mathbin {\supset } B$
to resemble material implication, and then the admissibility of
$A\mathbin {\supset } B$
to resemble material implication, and then the admissibility of
![]() $\gamma $
means that detachment for
$\gamma $
means that detachment for
![]() $\mathbin {\supset }$
is ok on theorems. Another way to view the
$\mathbin {\supset }$
is ok on theorems. Another way to view the
![]() $\gamma $
rule is as “disjunctive syllogism,” which has a fascinating history (cf. [Reference Anderson and Belnap2, §25], [Reference Anderson, Belnap and Michael Dunn3, §82]). Urquhart [Reference Urquhart51] provides an account of how Dunn and Meyer came up with their proof.
$\gamma $
rule is as “disjunctive syllogism,” which has a fascinating history (cf. [Reference Anderson and Belnap2, §25], [Reference Anderson, Belnap and Michael Dunn3, §82]). Urquhart [Reference Urquhart51] provides an account of how Dunn and Meyer came up with their proof.
Dunn proved that
![]() $\gamma $
is admissible for
$\gamma $
is admissible for
![]() $\mathbf {R}$
-mingle (
$\mathbf {R}$
-mingle (
![]() $\mathbf {RM}$
), which adds the mingle axiom (M)
$\mathbf {RM}$
), which adds the mingle axiom (M)
![]() $A\to (A\to A)$
to
$A\to (A\to A)$
to
![]() $\mathbf {R}$
. (Incidentally,
$\mathbf {R}$
. (Incidentally,
![]() $\mathbf {RM}$
was created by Dunn to parallel
$\mathbf {RM}$
was created by Dunn to parallel
![]() $\mathbf {EM}$
, which was suggested as a potentially interesting logic by Storrs McCall; see [Reference Anderson and Belnap2, p. 94], [Reference Bimbó and Michael Dunn13].) The addition of the axiom
$\mathbf {EM}$
, which was suggested as a potentially interesting logic by Storrs McCall; see [Reference Anderson and Belnap2, p. 94], [Reference Bimbó and Michael Dunn13].) The addition of the axiom
![]() $A\to (B\to A)$
to
$A\to (B\to A)$
to
![]() $\mathbf {R}$
reduces it to 2-valued logic; however,
$\mathbf {R}$
reduces it to 2-valued logic; however,
![]() $\mathbf {RM}$
is neither of those logics. Infinite Sugihara matrices, which are linearly ordered, are characteristic for
$\mathbf {RM}$
is neither of those logics. Infinite Sugihara matrices, which are linearly ordered, are characteristic for
![]() $\mathbf {RM}$
, but for instance,
$\mathbf {RM}$
, but for instance,
![]() $\ \vdash _{\textbf {RM}}(A\to B) \lor (B\to A)$
and
$\ \vdash _{\textbf {RM}}(A\to B) \lor (B\to A)$
and
![]() are not theorems of
are not theorems of
![]() $\mathbf {R}$
. In [Reference Dunn15], Dunn proved that
$\mathbf {R}$
. In [Reference Dunn15], Dunn proved that
![]() $\mathbf {RM}$
is pretabular, and its extensions that have a finite characteristic Sugihara matrix without
$\mathbf {RM}$
is pretabular, and its extensions that have a finite characteristic Sugihara matrix without
![]() $0$
admit
$0$
admit
![]() $\gamma $
. A similar pretabularity result was proved for
$\gamma $
. A similar pretabularity result was proved for
![]() $\mathbf {LC}$
(Dummett’s logic) in [Reference Dunn and Meyer38] by Dunn and Meyer.
$\mathbf {LC}$
(Dummett’s logic) in [Reference Dunn and Meyer38] by Dunn and Meyer.
![]() $\mathbf {R}$
-mingle turned out to be a very fruitful logic—despite its “not-quite-relevant” nature. The first relational (or Kripke-style) semantics for an intensional logic—beyond modal and intuitionistic logics—was defined for this logic. Dunn in [Reference Dunn18, Reference Dunn19] gave semantics for propositional
$\mathbf {R}$
-mingle turned out to be a very fruitful logic—despite its “not-quite-relevant” nature. The first relational (or Kripke-style) semantics for an intensional logic—beyond modal and intuitionistic logics—was defined for this logic. Dunn in [Reference Dunn18, Reference Dunn19] gave semantics for propositional
![]() $\mathbf {R}$
-mingle and first-order
$\mathbf {R}$
-mingle and first-order
![]() $\mathbf {R}$
-mingle using model structures with a binary accessibility relation. The linear order of Sugihara matrices might hint at a reason why such a semantics works; however, another novelty in the semantics is equally important. Namely, Dunn defined a 3-valued semantics, which is unlike the common 2-valued semantics for modal logics and for intuitionistic logic (cf. [Reference Kripke44–Reference Kripke45]). The third value is the result of a formula getting both “usual” truth values (i.e., T and F); that is, the motivation for the third value here is different than in
$\mathbf {R}$
-mingle using model structures with a binary accessibility relation. The linear order of Sugihara matrices might hint at a reason why such a semantics works; however, another novelty in the semantics is equally important. Namely, Dunn defined a 3-valued semantics, which is unlike the common 2-valued semantics for modal logics and for intuitionistic logic (cf. [Reference Kripke44–Reference Kripke45]). The third value is the result of a formula getting both “usual” truth values (i.e., T and F); that is, the motivation for the third value here is different than in
![]() for
for
![]() $\frac {1}{2}$
, or in Bochvar’s and Kleene’s 3-valued logics where truth-value gaps are introduced. Truth-value gluts have appeared, later on, in other logics, for instance, in
$\frac {1}{2}$
, or in Bochvar’s and Kleene’s 3-valued logics where truth-value gaps are introduced. Truth-value gluts have appeared, later on, in other logics, for instance, in
![]() $\mathbf {LP}$
(the logic of paradox).
$\mathbf {LP}$
(the logic of paradox).
The three-variable fragment of
![]() $\mathbf {R}$
-mingle (
$\mathbf {R}$
-mingle (
![]() $\mathbf {RM}_3$
) has a 3-valued linearly ordered characteristic matrix, which can be viewed as
$\mathbf {RM}_3$
) has a 3-valued linearly ordered characteristic matrix, which can be viewed as
![]() $\{\,-1,0,+1 \,\}$
with the usual
$\{\,-1,0,+1 \,\}$
with the usual
![]() $\le $
.
$\le $
.
![]() $0$
is its own negation; thus, the filter
$0$
is its own negation; thus, the filter
![]() $[0)$
contains an “inconsistent element.” Dunn in [Reference Dunn21] used this 3-valued logic to show that there is a three-element model of Peano arithmetic (
$[0)$
contains an “inconsistent element.” Dunn in [Reference Dunn21] used this 3-valued logic to show that there is a three-element model of Peano arithmetic (
![]() $\mathbf {PA}$
) that does not make formulas that are not theorems of
$\mathbf {PA}$
) that does not make formulas that are not theorems of
![]() $\mathbf {PA}$
true (but it makes all theorems of
$\mathbf {PA}$
true (but it makes all theorems of
![]() $\mathbf {PA}$
at least true). A similar result follows for type theory. These theories illustrate Dunn’s general theorem about 3-valued structures; the latter emerge, for instance, when the homomorphic image of a structure results by a(n operational) homomorphism that is not a relational homomorphism. Arithmetic and type theory may be formulated in the language of a relevance logic such as
$\mathbf {PA}$
at least true). A similar result follows for type theory. These theories illustrate Dunn’s general theorem about 3-valued structures; the latter emerge, for instance, when the homomorphic image of a structure results by a(n operational) homomorphism that is not a relational homomorphism. Arithmetic and type theory may be formulated in the language of a relevance logic such as
![]() $\mathbf {R}$
. If those theories contain the theorems of their 2-valued counterparts and admit the rule
$\mathbf {R}$
. If those theories contain the theorems of their 2-valued counterparts and admit the rule
![]() $\gamma $
, then an elementary proof of the absolute consistency of the 2-valued theories results. The difficult steps in carrying out this plan are (i) finding a suitable formulation of the relevant version of a theory and (ii) showing that
$\gamma $
, then an elementary proof of the absolute consistency of the 2-valued theories results. The difficult steps in carrying out this plan are (i) finding a suitable formulation of the relevant version of a theory and (ii) showing that
![]() $\gamma $
is admissible. An example provided by Dunn in [Reference Dunn20] pertains to Robinson’s arithmetic
$\gamma $
is admissible. An example provided by Dunn in [Reference Dunn20] pertains to Robinson’s arithmetic
![]() $\mathbf {Q}$
.
$\mathbf {Q}$
.
![]() $\mathbf {Q}_{\mathbf {R}}$
(with
$\mathbf {Q}_{\mathbf {R}}$
(with
![]() $0$
included) collapses into
$0$
included) collapses into
![]() $\mathbf {Q}$
. Roughly speaking, the culprit is
$\mathbf {Q}$
. Roughly speaking, the culprit is
![]() $0$
, or more precisely,
$0$
, or more precisely,
![]() $\lambda x.\,x\times 0$
being a constant function that (of course) yields
$\lambda x.\,x\times 0$
being a constant function that (of course) yields
![]() $0$
for any argument. Multiplication by
$0$
for any argument. Multiplication by
![]() $0$
is not unlike the combinator
$0$
is not unlike the combinator
![]() $\textsf {K}$
with reduction axiom
$\textsf {K}$
with reduction axiom
![]() $\textsf {K}xy \vartriangleright x$
, which “disregards” y, or in other terms,
$\textsf {K}xy \vartriangleright x$
, which “disregards” y, or in other terms,
![]() $\textsf {K}x$
is a constant function. Dunn proved that relevant Robinson’s arithmetic of positive integers is not
$\textsf {K}x$
is a constant function. Dunn proved that relevant Robinson’s arithmetic of positive integers is not
![]() $\mathbf {Q}(1)$
(2-valued
$\mathbf {Q}(1)$
(2-valued
![]() $\mathbf {Q}$
without
$\mathbf {Q}$
without
![]() $0$
). Then in [Reference Dunn23], Dunn formulated
$0$
). Then in [Reference Dunn23], Dunn formulated
![]() $\mathbf {OM\#}$
, arithmetic as an extension of orthomodular logic—owing to the craze in philosophy about the “One True Logic” (orthomodular logic) at the time. He demonstrated that
$\mathbf {OM\#}$
, arithmetic as an extension of orthomodular logic—owing to the craze in philosophy about the “One True Logic” (orthomodular logic) at the time. He demonstrated that
![]() $\mathbf {OM\#}$
, orthomodular arithmetic proves the distributivity of
$\mathbf {OM\#}$
, orthomodular arithmetic proves the distributivity of
![]() $\land $
and
$\land $
and
![]() $\lor $
. Furthermore, orthomodular logic with a minimal amount of extensionality collapses into 2-valued logic. Dunn continued to scrutinize the interactions between extensionality and components of a logic such as the constants
$\lor $
. Furthermore, orthomodular logic with a minimal amount of extensionality collapses into 2-valued logic. Dunn continued to scrutinize the interactions between extensionality and components of a logic such as the constants
![]() $\boldsymbol {T}$
and
$\boldsymbol {T}$
and
![]() $\boldsymbol {F}$
as well as theorems such as truth table generalizations of excluded middle in [Reference Dunn26]. He proved that such ingredients—independently of other features of a logic—suffice to reduce a higher-order logic to 2-valued higher-order logic. Dunn investigated applications of quantified relevance logics with identity to philosophical problems in a series of papers [Reference Dunn25, Reference Dunn27–Reference Dunn29, Reference Dunn34]. Often, distinctions are made between various kinds of properties such as intrinsic and essential properties, and there is no agreement in the philosophical literature as to existence being or not being a predicate. Relevance logics provide a more expressive framework than modal logics do (let alone fol does) to analyze such problems.
$\boldsymbol {F}$
as well as theorems such as truth table generalizations of excluded middle in [Reference Dunn26]. He proved that such ingredients—independently of other features of a logic—suffice to reduce a higher-order logic to 2-valued higher-order logic. Dunn investigated applications of quantified relevance logics with identity to philosophical problems in a series of papers [Reference Dunn25, Reference Dunn27–Reference Dunn29, Reference Dunn34]. Often, distinctions are made between various kinds of properties such as intrinsic and essential properties, and there is no agreement in the philosophical literature as to existence being or not being a predicate. Relevance logics provide a more expressive framework than modal logics do (let alone fol does) to analyze such problems.
Dunn also worked on the proof-theoretic aspects of relevance logics. He introduced
![]() $LR^+$
, a sequent calculus for
$LR^+$
, a sequent calculus for
![]() $\mathbf {R}_+$
, the positive fragment of the logic
$\mathbf {R}_+$
, the positive fragment of the logic
![]() $\mathbf {R}$
in [Reference Dunn16]. Relevance logics avoid proving
$\mathbf {R}$
in [Reference Dunn16]. Relevance logics avoid proving
![]() $A\to (B\to A)$
(the arrow version of the positive paradox) as a theorem, which means that the left weakening rule cannot be adopted as a rule in a sequent calculus. An innovation in
$A\to (B\to A)$
(the arrow version of the positive paradox) as a theorem, which means that the left weakening rule cannot be adopted as a rule in a sequent calculus. An innovation in
![]() $LR^+$
is that formulas can form two kinds of sequences that are indicated, respectively, by , and ;. Comma corresponds to
$LR^+$
is that formulas can form two kinds of sequences that are indicated, respectively, by , and ;. Comma corresponds to
![]() $\land $
, whereas semi-colon turns into
$\land $
, whereas semi-colon turns into
![]() $\circ $
on the left-hand side of the
$\circ $
on the left-hand side of the
![]() $\ \vdash \,$
, and weakening is a rule only for sequences built with comma. Another novelty in
$\ \vdash \,$
, and weakening is a rule only for sequences built with comma. Another novelty in
![]() $LR^+$
is the presence of
$LR^+$
is the presence of
![]() $\boldsymbol {t}$
, which is essential in applications of the cut rule where the left premise is a theorem (i.e., the
$\boldsymbol {t}$
, which is essential in applications of the cut rule where the left premise is a theorem (i.e., the
![]() $\ \vdash $
has nothing on the left). The insertion of
$\ \vdash $
has nothing on the left). The insertion of
![]() $\boldsymbol {t}$
instead of the invisible empty sequence precludes the conflation of the two kinds of sequences of formulas (and thereby, it prevents bogus proofs of non-theorems to count as proofs). Dunn in [Reference Dunn17] also showed that the most natural version of analytic tableaux in the style of Jeffrey formalizes fde (rather than 2-valued logic). Further, [Reference Dunn22] gave a straightforward step-by-step method to find out whether a 2-valued theorem of the form
$\boldsymbol {t}$
instead of the invisible empty sequence precludes the conflation of the two kinds of sequences of formulas (and thereby, it prevents bogus proofs of non-theorems to count as proofs). Dunn in [Reference Dunn17] also showed that the most natural version of analytic tableaux in the style of Jeffrey formalizes fde (rather than 2-valued logic). Further, [Reference Dunn22] gave a straightforward step-by-step method to find out whether a 2-valued theorem of the form
![]() $A\mathbin {\supset } B$
(with no
$A\mathbin {\supset } B$
(with no
![]() $\mathbin {\supset }$
in A or B) is an fde theorem
$\mathbin {\supset }$
in A or B) is an fde theorem
![]() $A\to B$
(with
$A\to B$
(with
![]() $\lnot $
rewritten as
$\lnot $
rewritten as
![]() $\mathop {\sim }$
).
$\mathop {\sim }$
).
The cut rule, in some form, is desirable in a sequent calculus, because it facilitates a proof of the replacement theorem as well as a proof of the equivalence of the sequent calculus formulation of the logic with its axiomatization. The cut rule, on the other hand, violates the subformula property; hence, its presence is sometimes undesirable. The admissibility of the cut rule, which delivers the benefits without the drawbacks, can be proved syntactically, but also semantically. Dunn and Meyer in [Reference Dunn and Meyer39] used insights from proofs of the admissibility of
![]() $\gamma $
to prove the admissibility of the cut for
$\gamma $
to prove the admissibility of the cut for
![]() $K_1$
, Schütte’s formulation of fol. This was the first conceptually new proof of the cut theorem for fol since the 1950s.
$K_1$
, Schütte’s formulation of fol. This was the first conceptually new proof of the cut theorem for fol since the 1950s.
Curry noted a similarity between certain combinators and structural rules in the sequent calculi
![]() $LK$
and
$LK$
and
![]() $LJ$
. The positive or the implicational fragments of the relevance logic
$LJ$
. The positive or the implicational fragments of the relevance logic
![]() $\mathbf {B}$
can supply the context to make this analogy precise. Dunn and Meyer in [Reference Dunn and Meyer40] introduced sequent calculi in which structural rules are fully supplanted by combinatory rules, hence the name “structurally free logics” for this group of logics. Indirectly, the ideas in structurally free logics together with the connections between implicational fragments of relevance logics and the simple principal type schemas of (proper) combinators led to a solution of an open problem by Dunn and Bimbó around 2010. [Reference Bimbó and Michael Dunn9] introduced a new sequent calculus for
$\mathbf {B}$
can supply the context to make this analogy precise. Dunn and Meyer in [Reference Dunn and Meyer40] introduced sequent calculi in which structural rules are fully supplanted by combinatory rules, hence the name “structurally free logics” for this group of logics. Indirectly, the ideas in structurally free logics together with the connections between implicational fragments of relevance logics and the simple principal type schemas of (proper) combinators led to a solution of an open problem by Dunn and Bimbó around 2010. [Reference Bimbó and Michael Dunn9] introduced a new sequent calculus for
![]() $\mathbf {R}_\to $
(denoted by
$\mathbf {R}_\to $
(denoted by
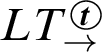 ), which extends a sequent calculus for
), which extends a sequent calculus for
![]() $\mathbf {T}_\to ^{\boldsymbol {t}}$
(from [Reference Bimbó6]). Then [Reference Bimbó and Michael Dunn10] showed how three sequent calculi,
$\mathbf {T}_\to ^{\boldsymbol {t}}$
(from [Reference Bimbó6]). Then [Reference Bimbó and Michael Dunn10] showed how three sequent calculi,
![]() $LR_\to ^{\boldsymbol {t}}$
,
$LR_\to ^{\boldsymbol {t}}$
,
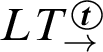 , and
, and
![]() $LT_\to ^{\boldsymbol {t}}$
, plus the decidability of
$LT_\to ^{\boldsymbol {t}}$
, plus the decidability of
![]() $\mathbf {R}_\to ^{\boldsymbol {t}}$
, can be combined to prove the decidability of
$\mathbf {R}_\to ^{\boldsymbol {t}}$
, can be combined to prove the decidability of
![]() $\mathbf {T}_\to $
, that is, the decidability of implicational ticket entailment.
$\mathbf {T}_\to $
, that is, the decidability of implicational ticket entailment.
The proof-search tree approach to decidability, which is based on sequent calculi and originated with Curry, was adapted to relevance logics (to
![]() $\mathbf {E}_\to $
and
$\mathbf {E}_\to $
and
![]() $\mathbf {R}_\to $
) by Saul A. Kripke. Meyer showed that
$\mathbf {R}_\to $
) by Saul A. Kripke. Meyer showed that
![]() $LR$
(lattice-
$LR$
(lattice-
![]() $\mathbf {R}$
) and
$\mathbf {R}$
) and
![]() $LR^\square $
(lattice-
$LR^\square $
(lattice-
![]() $\mathbf {R}$
with necessity) are decidable.
$\mathbf {R}$
with necessity) are decidable.
![]() $LR$
differs from
$LR$
differs from
![]() $\mathbf {R}$
by omitting the distributivity of conjunction and disjunction, and the
$\mathbf {R}$
by omitting the distributivity of conjunction and disjunction, and the
![]() $\square $
in
$\square $
in
![]() $LR^\square $
is like the “exponential” ! , which makes
$LR^\square $
is like the “exponential” ! , which makes
![]() $LR^\square $
similar to
$LR^\square $
similar to
![]() $LL$
(linear logic). [Reference Bimbó and Michael Dunn11] (cf. [Reference Bimbó and Michael Dunn12]) showed that
$LL$
(linear logic). [Reference Bimbó and Michael Dunn11] (cf. [Reference Bimbó and Michael Dunn12]) showed that
![]() $LL$
(which has been believed to be undecidable for decades) is decidable, like a handful of other closely related logics.
$LL$
(which has been believed to be undecidable for decades) is decidable, like a handful of other closely related logics.
Dunn claimed in his autobiography [Reference Bimbó7, p. xxix] that he had no grand research program. However, he invented a grand framework—gaggle theory—to deal with the semantics of substructural logics. The set-theoretical semantics that Dunn defined for
![]() $\mathbf {RM}$
did not seem to generalize to
$\mathbf {RM}$
did not seem to generalize to
![]() $\mathbf {R}$
or
$\mathbf {R}$
or
![]() $\mathbf {E}$
. After the introduction of the Meyer–Routley semantics [Reference Routley and Meyer49], together with the operational semantics of Urquhart [Reference Urquhart50] and the operational–relational semantics of Fine [Reference Fine42], Dunn started to develop a theory of set-theoretical semantics that would encompass a range of semantics somewhat similarly as the Jónsson–Tarski representation provides semantics for a range of logics the Lindenbaum algebra of which has a Boolean algebra reduct. Dunn gave the first “gaggle talk” in 1979, and presented the whole framework in a series of papers in the 1990s [Reference Dunn30–Reference Dunn33], and further, in two books in the 2000s [Reference Bimbó and Michael Dunn8, Reference Dunn and Hardegree37]. Gaggles (of various kinds) are algebras, many of which are reducts of the Lindenbaum algebra of intensional logics such as
$\mathbf {E}$
. After the introduction of the Meyer–Routley semantics [Reference Routley and Meyer49], together with the operational semantics of Urquhart [Reference Urquhart50] and the operational–relational semantics of Fine [Reference Fine42], Dunn started to develop a theory of set-theoretical semantics that would encompass a range of semantics somewhat similarly as the Jónsson–Tarski representation provides semantics for a range of logics the Lindenbaum algebra of which has a Boolean algebra reduct. Dunn gave the first “gaggle talk” in 1979, and presented the whole framework in a series of papers in the 1990s [Reference Dunn30–Reference Dunn33], and further, in two books in the 2000s [Reference Bimbó and Michael Dunn8, Reference Dunn and Hardegree37]. Gaggles (of various kinds) are algebras, many of which are reducts of the Lindenbaum algebra of intensional logics such as
![]() $\mathbf {R}$
or
$\mathbf {R}$
or
![]() $\mathbf {T}$
. (“Gaggle” also serves as the pronunciation of the acronym “gGl” that stands for generalized Galois logics.) This uniform approach to the definition of the semantics of substructural logics yields a semantics once (abstractly) residuated operations are grouped together, and their distribution types (if there are lattice connectives in the logic) or their tonicity types are discerned. An interpretation for a logic emerges in two steps: first, the Lindenbaum algebra of the logic is seen as a gaggle (or more likely, several gaggles combined), and second, the set-theoretic representation of the algebra yields the semantics. Hopefully, this description outlines the big picture; however, the details are many and subtle. Kripke’s semantics and the Meyer–Routley semantics dealt with non-classical logics of a certain kind, while Dunn’s gaggle theory is applicable not only to those logics but to logics without
$\mathbf {T}$
. (“Gaggle” also serves as the pronunciation of the acronym “gGl” that stands for generalized Galois logics.) This uniform approach to the definition of the semantics of substructural logics yields a semantics once (abstractly) residuated operations are grouped together, and their distribution types (if there are lattice connectives in the logic) or their tonicity types are discerned. An interpretation for a logic emerges in two steps: first, the Lindenbaum algebra of the logic is seen as a gaggle (or more likely, several gaggles combined), and second, the set-theoretic representation of the algebra yields the semantics. Hopefully, this description outlines the big picture; however, the details are many and subtle. Kripke’s semantics and the Meyer–Routley semantics dealt with non-classical logics of a certain kind, while Dunn’s gaggle theory is applicable not only to those logics but to logics without
![]() $\land $
and
$\land $
and
![]() $\lor $
distributing over each other, and even without one or both of the latter connectives. Furthermore, issues of canonicity, of correspondence between axioms and frame conditions, of topological characterizations of the image of the Lindenbaum algebra and of interactions between groups of operations are only some of the questions that have been investigated as part of generalized Galois logics. Gaggle theory combines an algebraic approach to logics—that was always preeminently present in Dunn’s work—with the goal of producing informally palatable interpretations for logics—that is in harmony with Dunn’s view of logics as tools for rational beings.
$\lor $
distributing over each other, and even without one or both of the latter connectives. Furthermore, issues of canonicity, of correspondence between axioms and frame conditions, of topological characterizations of the image of the Lindenbaum algebra and of interactions between groups of operations are only some of the questions that have been investigated as part of generalized Galois logics. Gaggle theory combines an algebraic approach to logics—that was always preeminently present in Dunn’s work—with the goal of producing informally palatable interpretations for logics—that is in harmony with Dunn’s view of logics as tools for rational beings.
This brief overview has been unavoidably selective. Dunn published (sometimes with co-authors) on other topics too, which include information, its properties, and its role in logic and computing; pieces of history of relevance logics and informal interpretations of those logics; the logic of quantum computers; relational algebras; etc. The complete list of publications of Dunn (up to about 2015) is included in [Reference Bimbó7], and hopefully the reader is intrigued by now to find out more about Dunn’s work and results in logic.
J. Michael Dunn was a highly respected logician whose legacy will thrive through his books and papers, through the knowledge of his students, as well as through his efforts to establish the Logic Program and to found the School of Informatics at Indiana University in Bloomington.



